构造向量求数列的和
2022-11-14 13:29215600江苏省梁丰高级中学
中学数学杂志 2022年4期
215600 江苏省梁丰高级中学
江苏省张家港市罗建宇名教师工作室 赵颖颖
向量是沟通几何与代数的桥梁,是进一步学习和研究其他数学领域问题的基础[1].在中学教学实践中,向量常作为工具来解决几何问题,也能解决一些代数问题,向量的运用多见于等式、不等式、函数等问题(参见文[2]-文[9]).笔者构造向量求几类典型数列的和,作为向量在解决代数问题中的补充,用以倡导在高中数学知识间进行相互论证,发展数学学力.
一、 构造向量推导等差数列前n项和公式
问题1设数列{an}是公差为d的等差数列,求数列{an}的前n项和.
解析:当d=0时,易得.下面推导当d≠0时的求和公式.
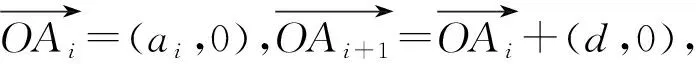
评注:从向量的视角看,等差数列对应向量的加减法运算,问题1的解决是在构造向量的基础上,结合向量的模的计算得以推导等差数列前n项和公式.类似地,利用上述对向量的模的计算方法,可以求数列{nm}(m∈N*)的前n项和,简析如下.
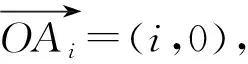
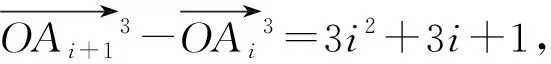
二、 构造向量推导等比数列前n项和公式
问题2设数列{an}是公比为q的等差数列,求数列{an}的前n项和.
解析:当q=1时,易得.下面推导当q≠1时的求和公式.
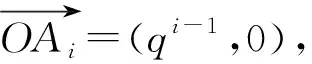
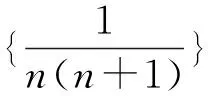
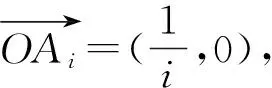
三、 构造向量求“等差×等比”数列前n项和
问题3设数列{an}是公差为d的等差数列,数列{bn}是公比为q的等比数列,求数列{an·bn}的前n项和.
解析:同上,这里只需解析当q≠1时的求和.
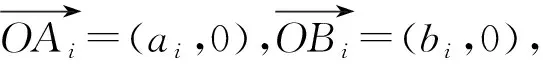
评注:问题3的解决常用经典的“错位相减法”求和,这里是在构造向量的基础上综合运用有关向量的线性表示,结合向量数量积运算求得“等差×等比”数列的前n项和公式.
猜你喜欢
汽车实用技术(2022年7期)2022-04-20
数学小灵通(1-2年级)(2021年9期)2021-10-12
数学小灵通(1-2年级)(2021年5期)2021-07-21
数学小灵通(1-2年级)(2021年6期)2021-07-16
中学生数理化(高中版.高考数学)(2019年10期)2019-11-08
中学生数理化(高中版.高考数学)(2019年10期)2019-11-08
中学生数理化(高中版.高二数学)(2019年9期)2019-09-28
中学生数理化(高中版.高考数学)(2018年10期)2018-11-07
中学生数理化(高中版.高二数学)(2018年10期)2018-11-03
中学数学杂志(高中版)(2016年1期)2016-02-23

