横向弯曲载荷作用下双体船极限承载能力分析

李 虎 吴淏堃 张 正 甘 进

(湛江南海西部石油勘察设计有限公司1) 湛江 524057) (宁波捷茂船舶技术有限公司2) 宁波 315040) (武汉理工大学船海与能源动力工程学院3) 武汉 430063)

0 引 言

与传统的单体船相比，双体船拥有甲板宽大，截面特殊的船型特点.其特殊的截面结构形式，使双体船的总纵强度容易满足，而在船宽方向上的截面变化剧烈，受横弯与扭转的影响显著，尤其是连接桥部分，是双体船结构设计过程中的关键.

自“极限承载能力”提出以来，基于极限强度的设计已逐渐取代基于线弹性范围内满足许用应力要求的设计.传统的船舶结构极限强度问题主要针对船体梁的纵向强度，研究方法主要有直接计算法、Smith法(逐步破坏法)、理想结构单元法、非线性有限元法以及模型试验法.直接计算法是基于现有船舶的数据基础上得到的，对双体船这一船型的适用性有待商榷.Smith法根据船舶的剖面特性，计算船体受总纵弯曲的极限承载能力较为简单易行，对于双体船这类受横弯与扭转影响较大的船型而言具有一定的局限性.理想结构单元法将一个结构体系离散成部分大的结构单元，将这些单元的材料非线性与几何非线性进行理想化处理，从而大幅度提高计算效率.然而理想结构单元法仍不能很好的模拟结构的后极限强度，且对于复杂载荷作用下的极限强度计算精度有限[1].因此，模型试验法与非线性有限元法是评估双体船极限强度的有效手段.模型试验法是揭示结构崩溃行为与屈曲模式最有效、最直观的手段.由于成本较高，很少进行实船试验，大部分试验研究对象为加筋板[2]或箱型梁[3].Xu等[4]进行了内河双体船的四点弯曲试验.Liu等[5]基于相似理论，设计了1/8比例的小线面双体船模型在横向对开力作用下的极限强度试验，并将有限元仿真结果与试验结果作对比，用以评估小水线面双体船实船结构的极限承载能力.冯欣润等[6]进行了弯扭组合作用下的小水线面双体船极限强度试验，试验表明，该类船型应当在片体与连接桥部分设置过渡区域，减缓薄弱区域的应力集中.

目前双体船强度问题的主要研究手段仍是有限元分析，研究内容着重于双体船整体强度计算，双体船局部强度计算与连接桥强度计算[7].然而有限元分析过程中，载荷的确定与施加方式因人而异，计算结果也不尽相同.文中以一艘33 m的双体客船为研究对象，建立了典型舱段的有限元模型，计算了双体船典型舱段在横弯载荷作用下的极限强度，分析加载过程中的应力分布与破坏顺序，讨论了网格尺寸与加载方式对双体船横弯极限强度计算的影响.

1 有限元理论

显式动力学分析步(ABAQUS/Explicit)的基本思路见式(1)～(3).其中：u通过某一时刻i系统所受的合外力求得该时刻系统的运动状态，再借由该增量步下系统的运动状态来求得下一时刻系统的运动状态，直至达到预设的最大增量步数.其本质在于采用中心差分法进行显式时间积分，借由多个时间增量完成模拟，相较于弧长法与阻尼因子法而言，不存在计算的收敛性问题，适用于复杂结构的求解.

(1)

(2)

(3)

显式动力分析步在求解时，必须保证时间步长Δt小于稳定性限制Δtstable才能确保求解过程的稳定性，即满足式(4)，其中ωmax为结构的最高阶固有角频率.

(4)

当加载速率达到某临界值时，在加载过程中任何时刻系统的状态都可以当平衡态处理，而准静态法的求解关键就是要设置合适的加载速率[8].若加载速率过快会导致求解结果的局部性，即产生应力波导致结构出现振荡,使原本的静态问题变为动态问题，引起材料力学性能的改变；而过慢的加载速率会使计算效率大大降低.判断加载速率是否合适的一个重要标准就是分析过程中结构模型的动能与其应变能之比，其数值小于5%则可以认为该问题的求解过程是准静态的.在满足此要求的前提下，尽可能选取大的加载速率，以提高计算效率.

2 双体船横向弯曲极限强度分析

2.1 载荷工况

双体船在航行过程中遭遇横浪时，若一个片体处于波峰，另一片体处于波谷，此时由于吃水不同，两个片体会产生浮力差，进而在连接桥部分产生横向弯矩.在有限元计算中，需要对横向弯矩进行等效，方便加载在实际结构上，利于计算进行.目前使用较为广泛的方法是中国船级社颁布的《海上高速船入级与建造规范》(下文简称《规范》)中，钢/铝质高速船船体结构直接计算指南所给出的方法.即将双体船所受的横向弯矩等效为横向对开力，作用在深度方向0.5d(d为吃水)的位置，并按向内作用与向外作用两种工况分别考虑，见图1.而实际计算时，先要把横向对开力看作分布在整个船体的分布载荷，再在每个强横框架上施加等效集中力[9].而该方法可能造成片体位置的应力集中，尤其是只在外侧加载时，应力集中现象最明显，见图2.

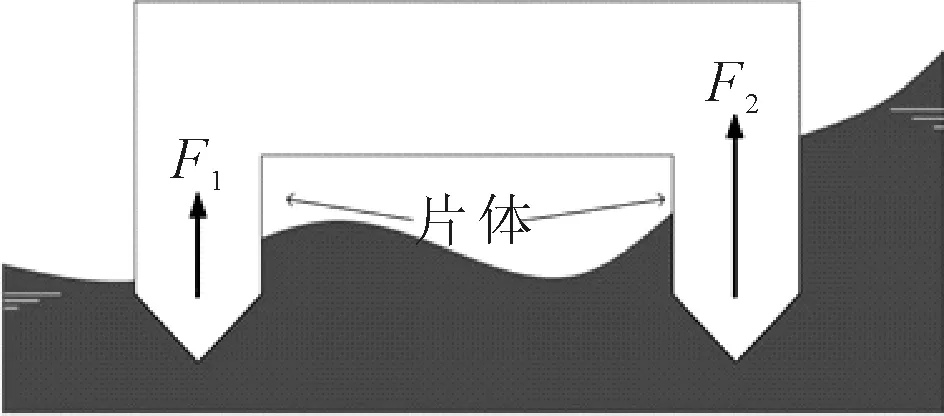
图1 双体船受波浪作用

图2 载荷示意图

2.2 计算模型

参考文献[5]可知，艏艉结构对双体船的横向抗弯强度贡献较小，在一些试验研究中，常常会为了降低工艺的难度而只对平行中体部分进行研究.为了降低计算成本，可以借鉴船体纵向强度的研究方法，仅对某典型舱段进行研究.记相邻两个横舱壁距离为S，选取(1/2)S+S+(1/2)S的部分作为研究对象.与传统的纵弯强度计算不同，由于横向弯矩是延船长方向分布，整船的横向极限承载能力随船长的增大而增大.因此，仅计算典型舱段的极限强度意义不大，但也可以表征船体受横向弯矩时的应力分布特点，或对某些参数进行分析讨论.

有限元模型中外板，横舱壁，隔板，内底板，强横梁与强肋骨的腹板采用S4R单元划分，强横梁与强肋骨的面板，普通横梁，普通肋骨采用B31单元划分.材料均采用Q235钢材，密度ρ=7.85×10-9t/mm2，弹性模量E=2.06×105MPa，泊松比μ=0.3，屈服极限为235 MPa.

舱段模型见图3，肋骨间距为500 mm，每四个肋位设置一个强框架，每隔四个强框架设置一道横舱壁.舱段模型中各构件尺寸见表1.

2.3 网格尺寸的影响

建立网格尺寸为(1/2)s，(1/4)s，(1/5)s，(1/10)s的有限元模型进行计算，得到双体船在横弯作用下的载荷-位移曲线见图4，曲线斜率为双体船的抗弯刚度.

图3 舱段模型示意图

表1 模型构件尺寸 单位：mm

图4 双体船舱段模型载荷位移曲线

表2 网格尺寸对计算结果的影响

由表2可知：网格尺寸越大，计算所得的极限承载能力越大.此外，不同网格尺寸的模型在线性段部分基本重合，而在非线性段，即结构开始发生屈服时，网格尺寸越大的模型，其刚度越大.因此，网格太大会导致计算结果偏保守，而网格尺寸太小会大大降低计算效率.综合考虑，将网格尺寸取为1/4s，可以在保证计算精度的同时提高计算效率.此时网格总数为84 815，其中S4R单元总数为83 409，B31单元总数为1 206.

图5为计算过程中的动能与内能变化曲线，图6为二者之比随时间的变化曲线.除了加载初期以外，加载过程中动能与内能之比始终在5%以下，故可以认为整个加载过程是趋于静态的，满足问题的“准静态”要求.

图5 动能与内能随时间变化曲线

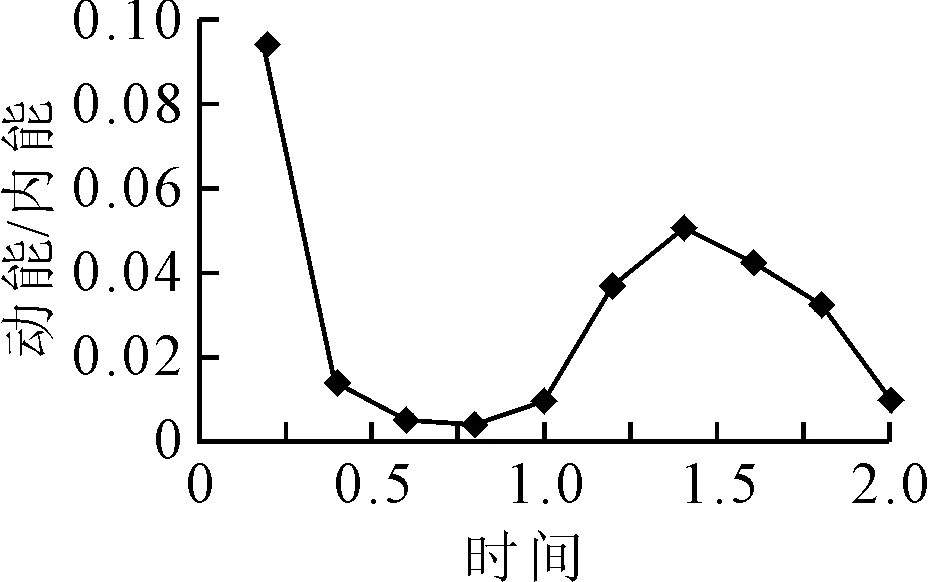
图6 动能与内能之比随时间变化曲线

2.4 加载方式对计算结果的影响

双体船所受横向弯矩其本质是两侧片体的浮力差造成的，故可以对一个片体固支，对另一个片体施加载荷，以此来达到中部连接桥承受横向弯曲作用的效果.本文进行了三种方案分析，方案一基于《规范》所给定的方案，对双体船艏艉施加固支约束，在两个片体吃水1/2d处施加大小相等方向相反的载荷，即横向对开力；方案二是对左侧片体底龙骨与肋板相交的节点处施加简支边界，右侧片体的该位置施加竖直向上的载荷；方案三是将左侧施加简支边界，右侧施加水平方向的载荷.三种方案载荷与边界的施加方法见图7.

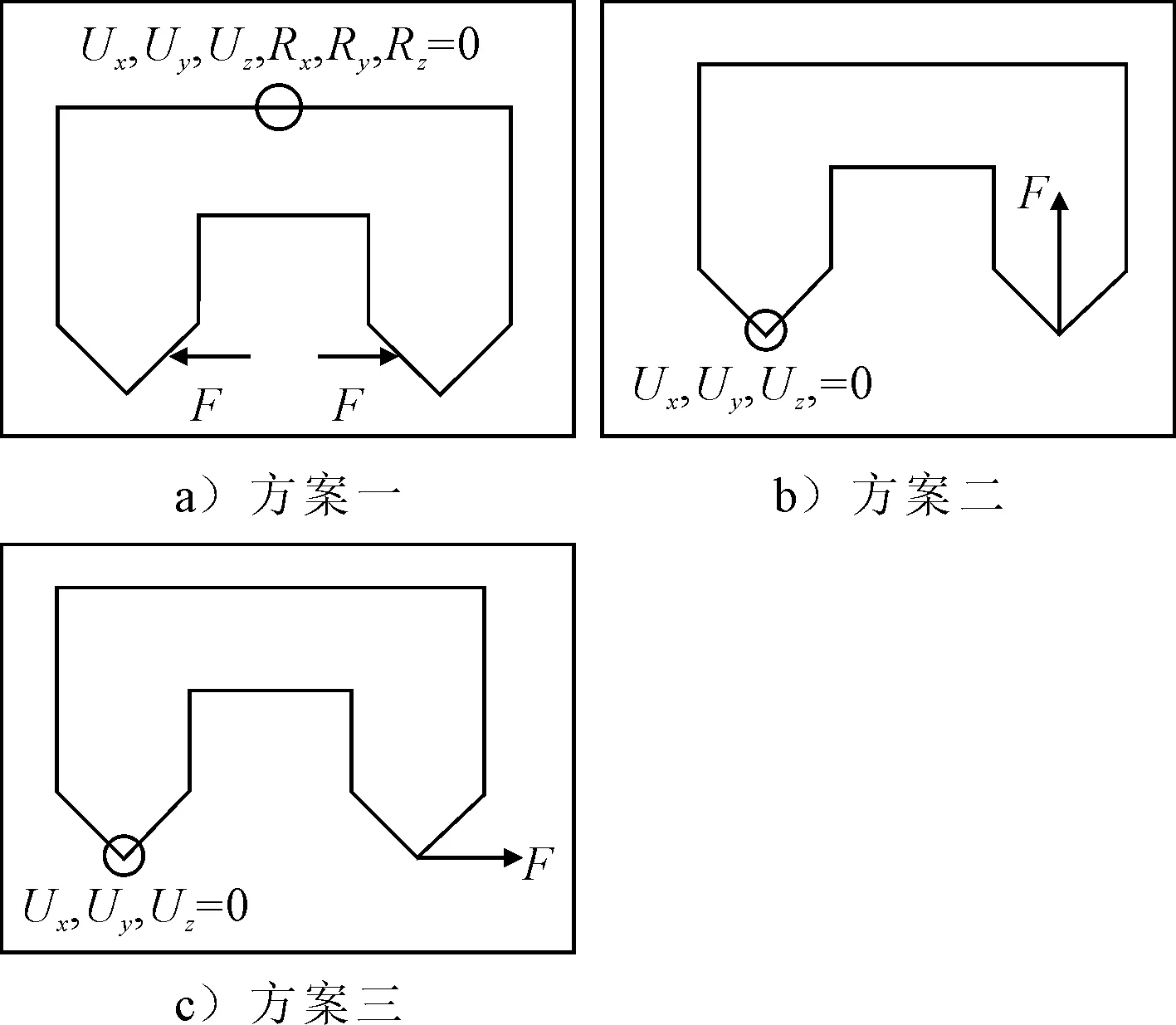
图7 三种方案的载荷与边界示意图

三种方案计算所得的极限弯矩见表3，改进的方案二三与《规范》所给定的方案一相比，计算所得的极限弯矩偏小，结果偏保守.

表3 三种方案的极限弯矩

2.5 横弯作用下双体船极限承载能力分析

由2.3节计算结果可知，舱段失稳过程可以分为图8的三个阶段，记为A，B和C阶段.舱段各组成部分失稳过程见图9.A阶段为开始加载时，整体结构还处于线弹性阶段，仅在舱壁与连接桥相交的角隅处有局部应力集中现象.由于船底肋板布置间距较密，整个船底相较于连接桥部分强度更高，此时船底的整体应力水平较低.

载荷继续增加，到达B阶段，连接桥甲板的应力逐渐增大，而片体甲板应力水平较低.舷侧的肋骨发生不同程度的侧倾，舱壁与连接桥相交的角隅处应力集中区域开始扩大，并发生了一定程度的塑性变形.此时，尽管有部分结构已发生屈曲失稳，但整体结构仍有承载裕度.

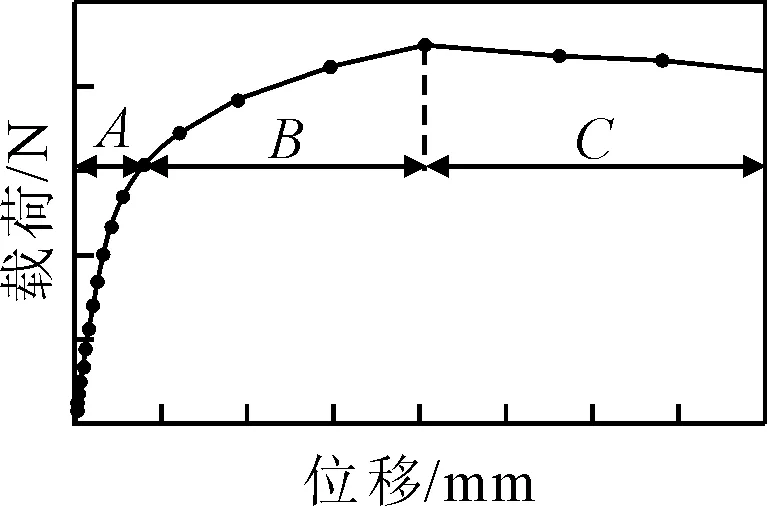
图8 模型失稳阶段

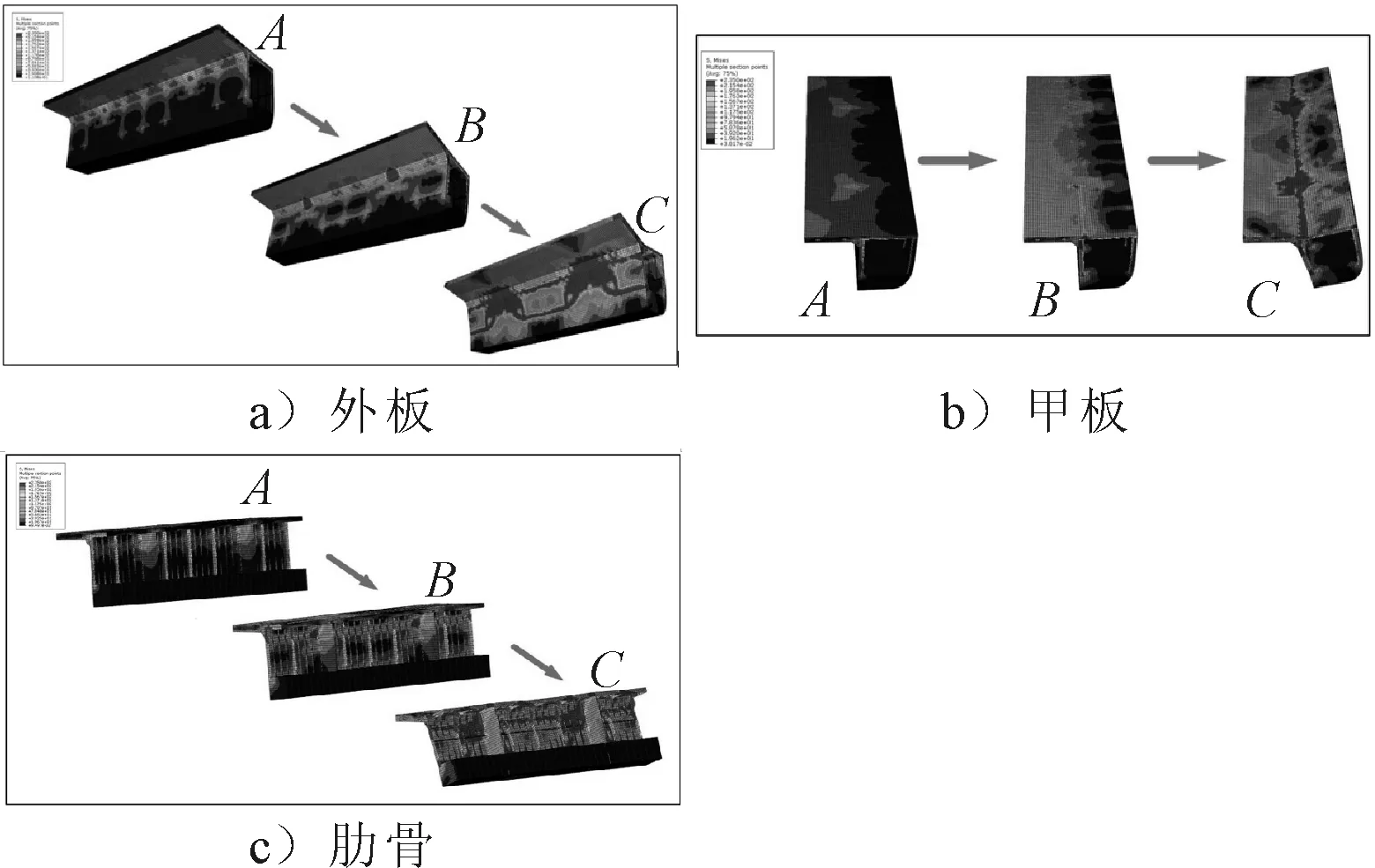
图9 舱段各组成部分失稳过程

之后继续加载，到达C阶段，连接桥与片体相邻的位置的应力不断提高，在二者的交线处形成一条屈曲带，并且伴随有局部的“鼓包”现象，而片体部分主要承受拉应力.肋骨与舷侧外板部分也发生整体屈曲，并在肋骨失稳处形成了一条平行于舷侧纵桁的屈曲带.直到载荷达到最大值，整体舱段处于极限状态.由于此时连接桥部分仍有较大的安全裕度，此时结构承载能力下降较为平缓，双体船舱段的破坏模式为片体与连接桥相连处的破坏.

由计算结果可知：双体船受横弯作用的薄弱位置是连接桥与片体的连接处，连接桥的甲板处会发生屈曲破坏，而片体会发生拉伸破坏，实际结构设计时，应重点关注该处的强度问题.可适当增加板厚或设置过渡区域以减缓角隅处的应力集中问题.在整个过程中，船底部分应力一直处于较低水平，设计时可以对该部分的板材进行优化，在保证结构安全性的同时适当减小板厚或改变肋板的布置形式，从而节省材料.

3 结 论

1) 双体船有限元分析中网格尺寸越大计算所得极限载荷会失真，结果偏保守，但可以提高计算效率，需要在分析过程中选取合适的网格尺寸.

2) 横向弯矩的作用下，双体船的整体破坏模式为连接桥与片体外板的相交处发生屈曲破坏.实际结构设计中，可以适当增加板厚、设置肋板或设置过渡区域，以改善此处的应力分布.

3) 双体船底部的安全裕度较大，当整体结构屈曲破坏时，船底肋板与船底龙骨仍有较大的承载能力，实际结构设计中可以适当减少底部骨材的布置，以节约成本.

4) 加载方式的不同会影响双体船计算所得的极限弯矩，改进的方案二、三相较于中国船级社所规定的方案所得结果偏小.