基于物流关系和非物流关系的邮轮分段车间布局优化

刘佳琦 徐 靖 杨家其 胡恒杰 骆奇峰 张霖波

(武汉理工大学交通与物流工程学院1) 武汉 430063) (上海外高桥造船有限公司2) 上海 200137)

0 引 言

我国高端邮轮建造市场还处于起步阶段，建造车间内的物流效益一直是建造过程评价的关键指标之一.如今船厂普遍采用分段建造模式开展船舶建造作业，即分段工位位置确定，工作人员、切割、焊机等加工设备，以及叉车、平板车等物流设备在各个分段间来回移动、作业.由于分段建造周期长，对车间场地、空间要求高，而车间内可以调配的加工和物流资源往往有限，且加工、物流设备自身的性能,以及相互之间的联系和作用又会影响到车间物料的搭载和后续物流环节如装卸和搬运的实施，因此物料加工流程的安排成为邮轮分段建造车间合理布局的关键环节[1].

分段建造过程主要包括堆放处提货、物料预处理、物料加工、部件拼接等多个环节，其中涉及到的设备有用于处理钢材和型材的大型加工设备，以及车间内实现物料运输的物流设备.邮轮分段车间涉及许多不同物料的加工流程，各加工流程之间既存在差异，也有一定的关联，不合理的车间布局容易导致物料搬运路线交叉干扰，加工和物流设备空置率高的问题.在考虑物料搬运路线的基础上，如何协调不同物料的加工流程，使车间的布局更加简洁、合理，作业环节连续性高，生产服务配套性强是目前分段车间物流优化所面临的难题之一.除此之外，分段车间布局优化还需要满足一系列定性和定量条件.

目前已有一些针对普通船舶的车间布局研究.雷明达[2]考虑船舶车间物料的合理配送路线，建立以物料搬运成本最小的单目标车间布局优化模型.张青雷等[3]在原有船舶动力生产车间的生产需求上，提出以物料搬运成本最少和车间占有面积最小的双目标车间布局优化模型，进一步提升了车间物流效益.在船舶物流流程优化问题上，陈卫彬等[4]把物料加工装配时间最短纳入考虑，并基于加工工件总作业时间最小求解船舶平面分段智能车间的物流系统优化问题.蒋岩[5]将物料订单可能的延误时间作为优化重点，进一步提升邮轮建造物资配货作业的效率.

综合来看，普通船舶的物料品种少，物流过程比较简单，涉及的车间布局问题和物流优化问题多以物料搬运成本最小或者加工时间最小的单目标优化模型为主，且很少从车间布局问题的角度出发对船舶车间的物流流程提出系统的优化方案.而对于多品种小批量生产的邮轮建造过程来说，复杂的物料品种和多层级的物流体系赋予了车间布局问题更为复杂的需求，对加工流程的连续性也提出了较高的要求.同时基于实际建造过程考虑，加工设备和物流设备的性能也会对物料搬运过程产生影响，所以设备之间的联系、加工流程的连续性等非物流关系均应在规划分段车间布局时纳入考虑，而这一水平通常用非物流关系密切程度作为衡量指标.结合以上分析，本文在邮轮分段建造车间面积和物料加工工序已确定的前提下，通过建立物料搬运成本最小和非物流关系密切程度最大的双目标规划模型，以物料在不同设备间整体工作流程作为切入点，探讨邮轮分段车间内设备布局的最优位置.

随着现代算法的发展，在研究车间问题时多选用粒子群算法进行求解.郭源源等[6]在粒子群优化算法中引入经典的系统布局规划法的思想，提升了粒子群算法在连续布局问题上的寻优效果.Hamed等[7]在粒子群算法中结合编码和解码技术进行单行设施布局问题的求解.于蒙等[8]在粒子群算法中考虑随遗传与迁移代数自适应调整参数的策略，使改进后的算法不易陷入局部最优.韩宜珂[9]为了克服粒子群算法容易陷入局部最优的问题，结合模拟退火算法高效地运用双目标函数得到了优化布局方案.

传统的粒子群算法在解决双目标的车间布局优化问题时，容易陷入“早熟”收敛，较难在局部最优和全局最优之间寻求到一个平衡点.为了最大可能得到全局最优的结果，文中在传统粒子群算法的基础上，引入一种自适应调整惯性权重，使惯性权重随着粒子适应度值的改变而改变，充分改善近似最优解的优化程度，有利于提升搜索精度和算法效率，得到可靠的全局最优解.

1 问题描述

布局问题的前提是设备单元的具体位置已经确定，而在邮轮分段车间布局中，需要确定的是车间内叉车、平板车等物流设备和切割机、焊机等加工设备的具体位置.因为物流设备如叉车、平板车相对加工设备所占空间面积较小，故在分析问题时只考虑它们的物料搬运功能，不考虑它们的尺寸.

假设每个加工设备单元形状都是标准的矩形，已知每个加工设备单元的尺寸，且它们以平行车间四周墙壁的方式放置.在分段车间实际生产中，物料的运输路线一般都是平行于车间墙壁的直线，所以在本文问题中，建立以车间左下角为坐标原点的坐标系，物料运输路线统一视为平行于X轴和Y轴.

符号表示上，车间在X和Y方向的长度和宽度分别用G、H表示，设有n个加工设备单元，θ={1,2,…,n}，对于∀i∈θ,有加工设备在X方向长度li和Y方向长度wi,设备中心坐标为(xi,yi).为符合车间内加工设备布置的实际情况，每个设备单元只能在某一行中出现一次，设备单元的总行数用m表示.

2 数学建模

考虑分段车间内物料配送路径和加工流程连续性的优化目标，建立单位时间内物料搬运成本最小Z1和非物流关系密切程度Z2最大的双目标函数表达式：

(1)

(2)

式中：Z1为物料搬运成本；Z2为非物流关系值；Pij为设备i和设备j之间单位物料单位距离的搬运费用；Qij为单位时间内设备i和设备j之间物料搬运量；dij为设备i和设备j之间的搬运距离，且i≠j，表达式为：dij=|xi-xj|+|yi-yj|；Fij为设备单元之间的非物流密切度等级.

bij为设备单元之间的密切度关联因子，它主要和设备单元间的实际搬运距离dij及最大可能距离dmax有关，具体取值见表1～2.

表1 设备关系密切度分类

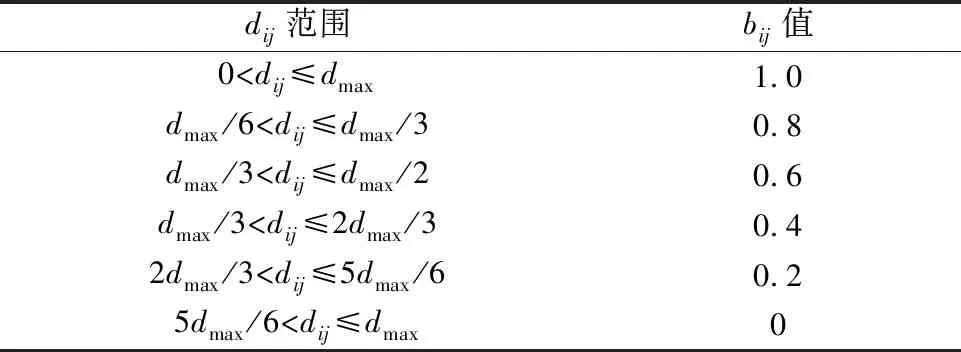
表2 密切度关联因子

dmax=G+H-2(G0+H0)

(3)

式中：G0为设备单元在X方向上与车间边界的最小距离；H0为设备单元在Y方向上与车间边界的最小距离.

为简化模型，将双目标函数转化为单目标函数Z：

(4)

式中：u1，u2为归一化因子，具体表达式为

(5)

(6)

式中：w1为物料搬运成本的权重；w2为非物流关系密切程度的权重，且w1+w2=1.

考虑邮轮分段车间的设备单元布局情况，约束条件表述如下.

1) 每个设备单元只能在某一行中出现一次，表达式为

(7)

i=1,2,…,nk=1,2,…,m

(8)

2) 相邻设备单元之间需要留有一定的距离，表达式为

(9)

式中：g为X方向上相邻两个设备单元之间必须保持的最小距离，g≥0，且为常数；lk(i)为第k行第i个设备单元在X轴上的长度.

同理Y方向上有：

(10)

式中：h为Y方向上相邻两行设备单元间必须保持的最小距离，已知h≥0,且为常数；wk(i)为第k行第i台设备在Y轴上的长度.

3) 设备单元在X、Y方向上的位置不能超过分段车间的边界.同时为了确保车间人员工作和物料配送的安全，各设备单元与车间的边界距离应设置一个安全范围内的最小值.为方便表达，将车间在X、Y方向上的边界也视为设备单元.

X方向左右两边的边界为

(11)

Y方向上下两边的边界为

(12)

X、Y方向与边界的最小距离约束为

(13)

(14)

3 基于自适应粒子群算法求解

3.1 编码设计

假设在需要优化布局的车间中有N个设备单元，把每种可能的优化方案看作一个粒子，则每个粒子的位置和速度都为2N维向量.位置向量中前N维代表设备单元在X轴上的坐标，后N维代表设备单元在Y轴上的坐标；速度向量中前N维代表粒子在X轴上的飞行速度，后N维代表粒子在Y轴上的飞行速度[10].位置P和速度V的具体坐标为

P=(x1,…,xn，y1,…,yn)

(15)

V=(vx1,…,vxn，vy1,…,vyn)

(16)

传统的粒子群算法中，粒子在第k次迭代时的飞行速度和位置更新公式为

(17)

(18)

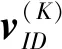
3.2 参数设计

1) 加速系数的确定 为避免算法陷入局部极值，需合理设置加速系数的取值.由文献[10]可知通常取c1=c2，且c1+c2≤4，根据经验，一般取值在[0.5，2]能够取得较好的优化结果.

2) 惩罚项 传统的粒子群算法不考虑约束条件，而在实际邮轮分段车间布局问题中，需特别考虑设备单元不能超过边界的约束条件.本文在改进的粒子群算法中增加一个惩罚项pe(i)，因为算法有自动换行机制保证设备单元在X方向上不会超过边界，所以只需判断车间的设备单元在Y方向上是否会超过边界，即

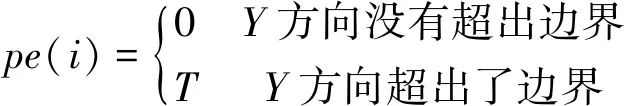
(19)

表达式中的T一般是较大的正数.本文T的取值为500.

3) 适应度函数 适应度函数是粒子群算法在运算过程中评价迭代效果和优化效果的重要函数，以保证实现全局最佳寻优的目的.结合目标函数，设置邮轮分段车间布局问题的适应度函数为

(20)

4) 惯性权重 粒子的全局与局部搜索能力之间的平衡与惯性权重的大小直接相关，迭代初期需要较大的惯性权重保持较强的全局搜索能力，后期则需要较小的惯性权重进行更加精确的局部搜索，同时也要尽可能地缩短运算时间，提高搜索效率.由文献[11]可知，惯性权重的调整主要受粒子适应度、种群规模以及搜索空间维度影响，所以在实际应用中，可以把惯性权重定义为

(21)

式中：Fi为第i个粒子的适应度值；N为搜索空间维度；n为粒子数目；a、b为经验参数.

算法在每次迭代后通过上式更新所有粒子的惯性权重，同时保证了局部寻优和全局寻优的准确性，提高了最优解的精度，有效地避免了陷入局部最优的可能.

4 实例检验

4.1 车间基本情况

以长170 m、宽170 m的邮轮分段生产车间为例，该车间主要设备有进行钢材和型材的半自动切割机、门式切割机和板条切割机、数控冷弯机、装焊设备和油压机等，主要得到产品有小组立、中组立、平台和零件等.为简化描述，按照邮轮分段车间的生产设备状况，用序号表示车间内各个设备组和堆放处，总计十个工作单元.其序号，名称及尺寸见表2.

表2 分段车间内作业单元尺寸 单位：m

考虑到邮轮分段车间中的实际情况，G0和H0分别为各设备单元在X轴和Y轴方向上应与边界必须保持的最小距离，G0=5.4 m，H0=4.3 m.X轴和Y轴方向上相邻两行设备间必须保持的最小距离g和h分别为0.8和0.4 m.

初始布局中设备单元原坐标向量为：X=[109 48 34 123 132 42 83 118 126 37]；Y=[105 20 101 81 55.2 74 52 31 15 38].

把设备单元间物料搬运线路视为直线，两设备单元间的距离可以用矩形单元中心的直角距离表示，物料搬运单价矩阵Pij、物料搬运量矩阵Qij和非物流关系密切程度分别见表3～6.

表3 分段车间内设备单元间的物料搬运单价 单位：m·件

表4 单位时间内分段车间设备单元间的物料搬运量

表5 非物流密切程度等级

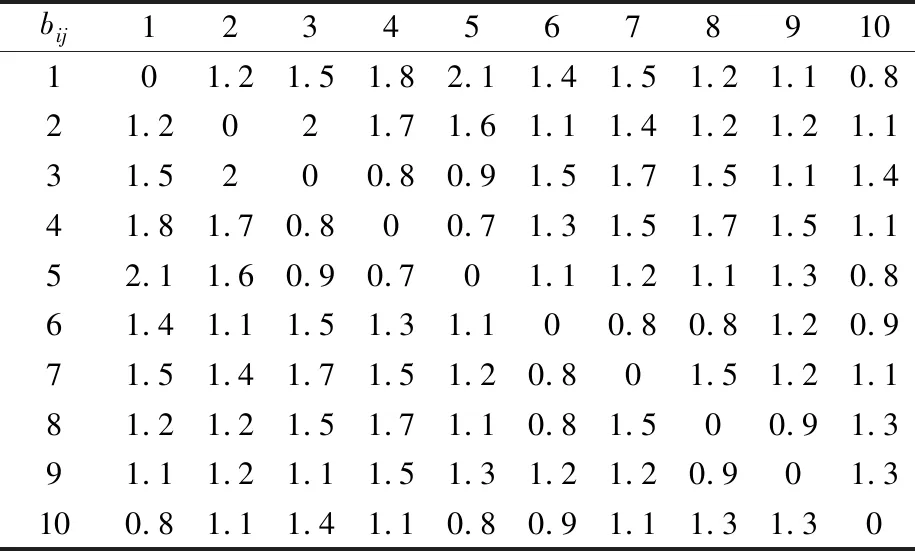
表6 非物流密切度关联因子

4.2 相关参数设置及优化步骤

在本案例中,对相关参数包括粒子维度(即工作单元数)D、种群规模(即粒子数)N、加速系数c1和c2、惯性系数w、迭代次数n、惩罚系数pe(i)进行设置，各参数具体数值见7.

表7 参数设置

由于粒子群算法的结果和迭代速度、加速系数具体的取值有关，为提高改进后粒子群算法的可靠性，本文在加速系数三种不同取值的情况下分别运行500次，选取每种加速系数较优的3次结果求平均值，然后对比分析它们的平均值大小.由于适应度值是目标函数的倒数，取最小的目标函数值，即取最大的平均适应度值作为最终的优化布局方案.

4.3 优化结果及分析

在Matlab软件上进行自适应惯性权重改进粒子群算法的求解过程，三种不同的加速系数运行得到的适应值及平均值结果见表8.

由表8可知：c1=c2=1.8时的平均适应度值最大，约为2.177 0×10-5，此时函数值最小，单位

表8 加速系数对比分析

时间内分段车间物料搬运成本和非物流密切程度的加权值最低，物流效益最大，故此方案优化效果最好，该邮轮分段车间布局优化方案下的结果约为4.941 2×105，比初始布局方案的结果9.296 3×105低，证明用自适应惯性权重改进粒子群算法求解邮轮分段车间布局优化模型的方法是有效的.根据求解结果，可以得出邮轮分段车间布局优化后的每个设备单元的位置坐标：X=[89.35 109.80 114.86 63.69 145.34 70.10 94.57 102.13 89.49 92.53]；Y=[75.15 108.46 75.34 103.05 56.22 58.48 96.06 101.06 101.07 76.13 116.93].

利用自适应惯性权重粒子群算法优化邮轮分段车间布局时，程序的迭代过程见图1.

图1 改进粒子群算法收敛过程

由图1可知：函数值在迭代进行到390次左右的时候基本达到稳定，说明算法的收敛能力良好，可以充分改善粒子群算法近似最优解的优化程度，更利于搜索全局最优解.

5 结 束 语

文中结合邮轮建造物料多品种小批量生产的物流特点，从邮轮建造现场工作实际出发，不仅考虑物料的搬运成本，同时聚焦不同物料加工工序间存在的重叠和干扰，以及设备自身性能等非物流因素对加工过程的影响，考虑引入非物流关系密切程度作为衡量加工流程连续性和设备自身性能等非物流因素的指标，在确定的分段车间面积和物料加工工序的前提下，以提升车间内部物流效益为目的，研究邮轮分段建造车间布局的优化方案.

通过建立基于物料搬运成本最小和非物流关系密切程度最大的双目标函数，引入动态惯性权重因子对传统的粒子群算法进行改进，使算法在全局搜索前期具有较高的探索能力，获得比固定惯性权重更为精确的寻优结果，更好地解决双目标的车间布局优化问题.同时为了确保各设备单元均不超过边界，也不互相干扰，在适应度函数上加入了基于约束条件的惩罚函数，进一步提升方案的可靠性.

结合邮轮分段建造车间实例验证，将优化后的邮轮分段车间布局方案同原始布局方案进行比较，发现基于物料搬运成本和非物流关系优化的邮轮分段车间布局方案能在保证整体工作流程贴近实际的基础上，通过降低物流成本，提升不同加工设备、物流设备和加工工序的连续性，显著提高分段车间物流过程的效益，双目标规划模型能够较好地从车间整体物流角度出发规划车间布局.