一种用于两人零和博弈对手适应的元策略演化学习算法

吴哲 李凯 徐航 兴军亮,

两人零和博弈作为博弈论中的一种基础模型,由于其兼具理论性完备、适应性广泛的特点,一直是人工智能领域所关注的重要问题.近年来,得益于以深度学习[1−2]为代表的一系列新技术的发展与应用以及计算能力的飞速提升,两人零和博弈中的一些比较困难的问题诸如围棋[3−7]、德州扑克[8−9]等已经取得了突破性的进展[10].

围绕纳什均衡解概念[11]进行求解是目前解决两人零和博弈问题主流的研究思路,由此产生的一系列均衡求解算法也得到了广泛的研究与发展.但是随着人们研究的进一步深入以及现实世界关于对抗问题的广泛关注[12],这种均衡求解方法暴露出越来越多的局限性.首先,对于状态空间较大的复杂博弈,寻找纳什均衡解的计算成本很高[13].例如求解德州扑克中的纳什均衡策略需要在整个博弈树上不断迭代求解,该过程需要计算集群巨大的算力支持和TB 级别的存储空间[14].同时,近似纳什均衡解的质量并不理想[14],在两人无限注德州扑克中的近似纳什均衡解可以被简单的局部最佳响应策略剥削.其次,求解纳什均衡解的前提条件是假设玩家双方是完全理性的,但是现实世界中更多面对的是非完全理性的竞争对手.这也就意味着采取均衡解要放弃剥削非理性对手带来的巨大潜在收益[15].

对手建模是均衡求解法之外的另一种在两人零和博弈中被广泛研究与使用的方法[16−18].与逼近纳什均衡解来保证最坏情况下的收益不同,对手建模方法通常需要基于历史数据来为当前的对手策略拟合一个显式模型,再根据该模型预测对手下一步的动作,以此作出更有针对性的决策来获取超额收益.但这种方法也有明显的局限性: 一方面,对手建模类方法由于需要历史交互数据来刻画一个显式的对手模型,因此交互数据的质量和规模都会影响模型刻画的准确性和时效性;另一方面,对手建模类方法所刻画的对手模型具有很强的针对性,一旦对手策略发生了改变,往往需要从零开始重新建立一个模型.

正是考虑到两人零和博弈领域内现有方法的局限性,本文创新性地提出一种在博弈过程中可以快速适应未知风格对手的元策略演化学习算法.本方法不以纳什均衡为求解目标,因此可以获取远超均衡解的收益,同时又避免了对手建模类方法对大量交互数据的需求.图1 展示了本方法的训练流程.

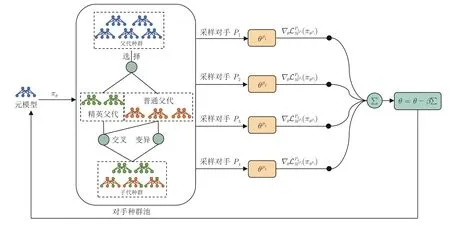
图1 本文提出的元模型训练方法Fig.1 The meta-model＇s training process

本文的研究重点和贡献可以被总结为三点.1)将元学习思想引入两人零和博弈过程,训练一个元模型用于未知风格对手的快速适应.这种快速适应的能力得益于元学习的策略更新方式,经过训练后的元模型收敛于参数空间内的一类初始点.该类初始点具有快速更新至目标参数空间的良好性质.2)提出了一种基于进化算法的种群训练方法用于提升元模型的泛化能力.由于元模型需要在参数空间内充分探索以寻找到最佳的初始点,因此本文提出一种基于进化算法的种群训练方式来为元模型的训练不断提供对手.一方面,该种群可以借助进化算法中的交叉(Crossover)、变异(Mutation)算子来不断探索更大的参数空间.另一方面,进化算法中的选择(Selection)算子通过不断筛选出优质对手来进一步提升元模型的博弈水平.3) 提高了种群演化算法的训练效率.元模型在训练期间会周期性地补充到种群中去,实现了进化算法多样性和梯度算法高效性的充分结合.

1 相关工作

1.1 均衡解求解

在两人零和博弈中,若存在这样的一个策略组合: 每个策略都是其他策略的最佳响应,那么这一策略组合便被称为纳什均衡策略组[19].在这个策略组中,每一个玩家都不可能因为单方面改变自身策略而增加收益.而且在任何一个有限两人零和博弈中都必然存在纳什均衡[19−20].因此,求取近似纳什均衡解来保证最坏情况下的收益,成为了目前两人零和博弈问题下主流的解决方案.

该类方法目前大多以自博弈 (Self-play)框架为基础[11],其中比较典型的做法是神经虚拟自博弈算法 (Neural fictitious self-play,NFSP)[21].Deep-Mind 的Lanctot等[22]基于Double oracle 算法提出一种更加通用的均衡求解框架PSRO (Policyspace response oracles),该算法可以看作是NFSP思想的进一步拓展.Zinkevich等[23]则创新性地提出了一种同样具有良好理论保证的近似均衡求解算法: 反事实遗憾最小化算法(Counterfactual regret minimization,CFR),其成为此后构建德州扑克智能体的主流算法[24−26].MCCFR[27]和DeepCFR[28]则分别结合了蒙特卡洛采样和深度神经网络近似的方法来克服传统CFR 方法中采样效率低、存储空间大的问题.但目前这一系列方法仍然面临以求解均衡策略为目标所带来的计算成本高和策略保守无法最大化剥削非理性对手的固有缺点.

1.2 对手建模

与追求纳什均衡的目标不同,对手建模方法旨在通过为对手建立模型来推测其意图,从而作出针对性决策以获取更高收益.常用的对手建模方法可分为显式建模、策略匹配、递归推理等几大类[16].

显式建模类方法[17]通常基于与对手的大量交互数据针对性地构建一个模型,以推测对手的决策意图.这类方法的缺点是对交互数据的需求量大,且需要不断更新当前的对手模型.策略匹配类方法[29−30]通常会建立一个离线数据库,在与对手的交互过程中为其匹配策略库中的相似模型,来预测对手的动作.这类方法虽然省去了从头建立对手模型的步骤,但是受限于离线数据库的规模,只针对特定对手有效.递归推理类方法[31]考虑的是嵌套推断这类更复杂的决策过程 (即我让你以为我在思考什么).这类方法的隐患是在诈唬对手的同时可能会被更狡猾的对手反利用.与以上这些需要大量交互数据来建立对手模型的方法不同,本文提出的方法并没有显式建立对手模型,而是通过不断采样不同风格的对手进行训练,以此获得快速适应的能力.

1.3 元学习

元学习目前已逐渐成为机器学习领域内一个新的研究热潮,解决的是让智能体学会去学习(Learning to learn) 的问题.该方法在训练过程中充分利用各个采样任务中获得的经验,将其泛化到新环境或新任务.元学习目前已经在监督学习领域中的分类和回归任务以及强化学习领域的新任务适应问题中取得了一系列进展[32−33].本文借助元学习快速适应的特点来克服传统博弈求解方法中存在的策略适应性差、交互数据需求量大等弊端.

目前针对元学习的研究主要集中于以下三类:1)距离度量类方法[34],通过学习不同任务之间的距离度量,从而达到在距离空间内快速适应新任务的目标;2)基于循环神经网络的元学习类方法[35],通过建立记忆系统来匹配面对新任务的决策模式;3)与模型无关的元学习类方法[32],主要通过训练得到一个比较好的网络初始化参数来加速适应过程.本文主要结合第三类元学习方法试图在决策空间内找到一组比较好的网络初始化权重,从而在面对未知对手时可以进行快速适应.

1.4 演化算法

演化算法 (Evolutionary algorithm,EA)[36]作为一类通用的搜索优化算法,在人工智能领域得到了广泛应用.该算法的一大优点是可以在不掌握目标函数及其梯度信息的情况下,仅依靠迭代评估可行解的好坏来逼近全局最优解.一些最新的群体智能算法通过引入演化算法的思想,已经解决了多类博弈问题[37−39].Jaderberg等[38]于2019 年发表在Science 上的工作就是借助种群训练(Populationbased training)[37]的思想对博弈过程中的群体模型进行超参数优化.它使用选择算子将当前模型权重替换为种群中表现最好的模型权重,并使用变异算子对模型超参数进行随机扰动.DeepMind 的Liu等[39]将演化算法应用到了合作类型的多智能体足球博弈场景中,通过配合使用选择、交叉、变异算子,使智能体在足球博弈场景中学会了复杂的合作策略.

2 两人零和博弈中的快速适应算法

本文所提出的适用于两人零和博弈的快速适应算法会在本节内进行详细介绍.本算法的目标在于,克服传统两人零和博弈中均衡求解法不具备策略适应性和对手建模方法对数据量要求大的固有缺陷.本算法创新性地将元学习方法引入博弈求解过程,并使用种群演化算法[40−41]为元模型的训练提供对手模型,克服了元学习方法依赖手工设计训练任务的弊端.

算法整体架构如图1 所示.本算法主要包含元模型训练器 (见第2.2 节)和对手种群演化池 (见第2.3 节) 两个模块.元模型训练器的目标是优化得到一个元模型,该元模型在决策空间内拥有良好的策略初始化.在面对未知风格对手时,能够通过少量交互来快速适应其策略,使得元模型收益尽可能大.为了提升元模型的泛化性,对手种群演化池在训练过程中不断提供训练样本给元模型.与传统元学习方法在图像分类、检测等任务中需要手工设计任务集不同,对手种群通过进化算法为元模型的训练提供了一套自动的课程学习[42]方案.

2.1 问题建模

为确保整个算法的通用性和可拓展性,元模型M使用深度神经网络πθ进行建模,用于训练的对手P被建模为πϕ.由此元模型与对手交互的过程可以建模为两人马尔科夫博弈[5]过程:

其中,S为状态空间,AM和AP分别代表双方玩家的动作空间,系统的状态转移方程定义为T:S ×AM ×AP →∆(S′),玩家的奖励函数Ri:S×AM×AP ×S′ →R 取决于当前状态S、下一个状态S′以及双方玩家的动作.在给定一个策略已知且固定的对手P的情况下,上述定义的两人马尔科夫博弈G就会退化为单人马尔科夫决策过程 (Markov decision process,MDP)[43]:

2.2 元模型训练算法

其中,α代表学习率,代表元模型πθ面对固定对手Pi的损失函数,γ代表折扣因子,MPi用于表示更新后的元模型.为了提升元模型的泛化能力,中的对手策略不断被采样并完成上述梯度更新过程.算法最终的目标是使得元模型可以快速适应每一个当前对手Pi并最大化平均奖励,即目标函数为:

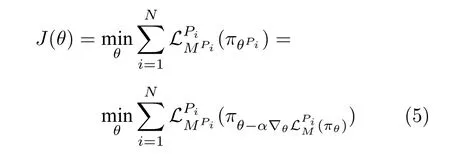
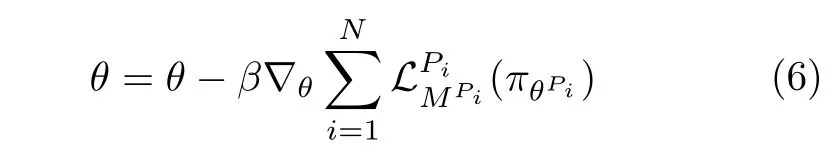
其中,β代表元模型参数更新的步长.

针对该优化目标进行求导后得到:

其中,τ′代表适应性参数θ′采集的轨迹.该优化形式与MAML (Model-agnostic meta-learning)类元学习算法[32]的优化目标一致.结合Finn 给出的理论保证[45],只需选用任意一个可进行自动微分的机器学习框架(例如PyTorch[46])对上述优化形式进行实现,训练后的元模型理论上就可以获得快速适应新对手的能力.由于式(7)中二阶梯度项的存在,算法整体的计算复杂度约为 O (d2),d代表博弈空间的问题维度.为了降低算法复杂度,本算法可采取MAML类元学习算法的通用实现方式,将二阶梯度项忽略,此时算法复杂度降低为 O (d),且整体效果不会受到较大影响[32].

总结来看,使用上述目标函数进行梯度更新的训练算法旨在找到这样一个元模型: 仅需与对手进行少量交互(即只进行几次梯度更新)就可以学会如何适应对手策略并剥削(奖励最大化).元模型训练算法的具体步骤详见算法1.种群演化对手策略生成(Opponent strategy generation,OSG)模块将在第2.3 节进行详细阐述.

算法1.元模型训练算法

该算法主要包含两个阶段,首先通过种群演化算法得到训练用的对手策略集合,然后再通过元模型训练算法得到快速适应性.第2.3 节对种群演化算法进行描述.

2.3 种群演化对手生成

在迭代开始前,首先随机初始化一个对手策略的种群B={P1,P2,···,PN},此时元模型策略M也会被补充到对手种群中,用于引导对手策略在演化初期快速提升博弈水平,提高训练效率.

种群策略的初始化完成以后,使用元模型来评估当前种群中每一个对手策略的适应度.适应度F被形式化为对手策略Pi与元模型在一个对局步长内获得的累计奖励总和:

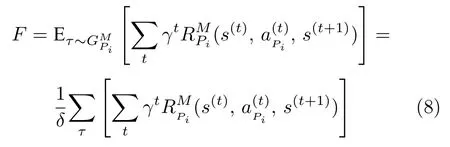
评估结束后,选择 (Selection) 算子基于当前种群策略的适应度,以ϑ的比例挑选出适应度靠前的部分个体组成精英团体E.对手种群池中剩余部分的策略 (B −E) 通过与精英团体E内的策略进行交叉 (Crossover) 以及自身策略的变异 (Mutation),来获得提升策略适应度的机会.精英团体E内策略的基因会完整保留到下一代种群中,不会受到交叉和变异算子的影响,这使得种群内部表现优异的基因(网络权重)可以不断延续下去.

本节所提出的种群演化算法通过不断自动生成对手策略来为元模型提供训练数据.选择算子的应用使得对手种群的博弈水平逐步提升,从而为元模型的训练构建了一个课程学习的范式.同时,交叉和变异算子的应用丰富了种群策略的多样性.用于训练的对手策略风格越多样,元模型的泛化能力就越强.算法2 详细描述了种群演化对手生成的具体步骤.

算法2.种群演化对手生成算法

本文中种群策略池的规模设定主要考虑了环境复杂度和算法收敛速度两个方面,统一设置为10.精英团体E占种群策略的比例ϑ根据不同问题在0.2∼0.5 内取值.变异率m utprob根据不同问题在0.1∼0.3 内取值.变异强度 m utstrength设置为0.1,即对应10%的高斯噪声.

3 实验评估

本节通过构建一系列对比实验,来验证本文所提出的元模型训练算法在两人零和博弈中的有效性.第3.1 节给出了用于实验评估的仿真环境和基线算法介绍.第3.2 节给出了算法训练及测试过程中的详细参数设置.第3.3 节对实验结果进行对比分析.

3.1 评估环境与基线算法

3.1.1 评估环境

本文所提出的算法在Leduc 扑克、两人有限注德州扑克 (Heads-up limit Texas Hold＇em,LHE)以及复杂连续空间下的仿真器RoboSumo[33]上都进行了实验验证.这些环境是目前两人零和博弈研究中被广泛使用的验证平台,其中两人有限注德州扑克和RoboSumo 均具有较高的环境复杂度,同时又分别属于离散和连续动作问题,因此能够充分评估算法的适应性和可拓展性.

环境具体介绍如下: Leduc 扑克通常包含两种花色(红桃、黑桃),每种花色有三个牌型(J,Q,K),共计6 张牌组成.整个游戏分为两轮,每个玩家在第一轮分别会得到一张私有牌,第二轮则只发一张公共牌.当有一方玩家的私有牌与公共牌组成对子时,则获得胜利;若无人组成对子,牌力高的一方获得胜利.胜利的一方赢取所有筹码,牌力相同时平分场上所有筹码.在发牌前,每个玩家会被强制下注1 个筹码,接下来的两轮下注中,每轮最多允许有两次加注,筹码量被分别固定为2和4.

两人有限注德州扑克是现实世界德扑玩家常用的一种扑克玩法.LHE 共包含52 张牌,游戏总共有4 个阶段,每个玩家在翻牌前阶段 (Pre-flop) 会得到2 张私有牌,在后续的翻牌阶段 (Flop)、转牌阶段 (Turn)、河牌阶段 (River) 会分别发出3 张、1 张、1 张,总共5 张公共牌.玩家在每个阶段的可选动作包括 “过牌 (Check)”、“加注 (Raise)”、“跟牌(Call)”、“弃牌 (Fold)”.若无人弃牌则牌力高的一方获得游戏胜利.

RoboSumo 是一个高维连续状态动作空间下的仿真机器人环境.本文中所用的RoboSumo-ants 仿真了两只蚂蚁在圆形擂台上角力的竞争型博弈过程.游戏获得胜利的条件是,将另一方推出擂台或掀翻.如果达到时间限制,该局比赛则以平局结束.该环境中每个玩家的状态空间由自身的可观测信息和对手的部分可观测信息组成.玩家自己的可观测信息包括自身关节的位置、速度和接触力,对手的部分可观测信息主要包括对手关节的位置.

3.1.2 基线算法

为验证元模型训练算法的优越性,本文与前面所介绍的求解两人零和博弈中的经典方法进行了实验对比.具体使用的基线算法如下.

1) CFR[23].反事实遗憾最小化算法CFR 被广泛应用于求解两人零和博弈中的近似纳什均衡解.2) DRON (Deep reinforcement opponent network)[17].DRON 方法将对手建模算法与深度强化学习相结合,在交互过程中推断对手类型并进行剥削.3) EOM (Explicit opponent modeling)[16].EOM是一种显式对手建模方法,通过收集大量对手交互数据来拟合对手模型并进行针对性求解.4) NFSP[21].NFSP 通过结合虚拟自博弈与深度强化学习算法,来求取两人零和博弈中的近似均衡解.5) MAML[32].元学习算法MAML 已经被成功应用于各种回归、分类以及单智能体强化学习任务.6) Oracle[17].Oracle 代表了在两人零和博弈中针对当前对手的近似最佳响应.7) 本文算法 +PPO.“本文算法 +PPO”代表将元模型的求解器由TRPO (Trust region policy optimization)[47]替换为计算效率更高的近端策略优化算法 (Proximal policy optimization,PPO)[48].8) 本文算法 −EA.“本文算法 −EA”代表在本文所提出算法中移除掉种群演化模块,仅使用元模型更新算法.9) EA.EA 算法仅使用种群演化算法[36],不使用元模型的更新方式.

上述基线算法中的1)和4)是两人零和博弈中求取近似纳什均衡解法的代表性方法,基线算法2)和3)是两人零和博弈对手建模解法中隐式建模和显式建模的代表性方法,基线算法5)是单智能体领域元学习解法的代表性方法.本文将MAML 训练所需的任务分布替换为对手策略分布,在每次迭代中,从中采样一批对手进行交互并完成元模型的更新.由于真实博弈过程中的对手策略分布并不会被玩家预先知晓,因此MAML 类算法仅能依靠随机生成的对手进行训练.基线算法6)代表了理想情况下的最佳响应.因此,使用上述基线算法与本文所提出的元模型训练算法进行对比,可以充分验证算法的有效性.

3.1.3 实验参数设置

本文使用带有GAE (Generalized advantage estimate)[49]的TRPO 算法[47]作为元模型的求解器,也可选用PPO[48]或其他任意梯度优化算法.模型架构为两层全连接网络,激活函数选择ReLU[50].本文所有的训练与评估都在一块NVIDIA TITAN Xp GPU 上完成,算法通过PyTorch 框架[46]进行部署.详细实验参数见表1.本文中报告的所有实验结果都是在设置3 个随机种子运行后得到的平均值.表2和表3 中扑克类环境的结果在每个随机种子下重复对打10 000 局后统计得出,代表的是该统计结果下的标准差.图2 中RoboSumo 的实验结果在每个随机种子下重复对打500 局后统计得出.图3内曲线部分的阴影代表了3 个随机种子下统计结果95%的置信区间.图 4 的实验结果为对打10 000 局后统计得出.图5 内曲线部分的阴影含义与图3 相同.

图2 本文算法与基线算法在RoboSumo 中的对比Fig.2 Comparison of our method with the baseline algorithm in RoboSumo

图3 消融实验Fig.3 Ablation study

表2 本文算法与基线算法在Leduc 环境中的对比Table 2 The average return of our method and baseline methods in Leduc

表3 本文算法与基线算法在LHE 环境中的对比Table 3 The average return of our method and baseline methods in LHE

3.2 实验结果与分析

3.2.1 元模型有效性验证

本节用于验证元模型训练算法的有效性.首先,对训练得到的元模型的快速适应性进行验证.模型的适应过程被限制为与当前对手只进行三步梯度更新,通过统计每步梯度更新后的平均收益来观测当前元模型的适应能力.其次,快速适应后的元模型被进一步用于与各类基线算法进行对比,通过统计与各类对手10 000 局对战的平均收益来观测各类算法的表现情况.在不同任务上的具体实验参数设置见表1.

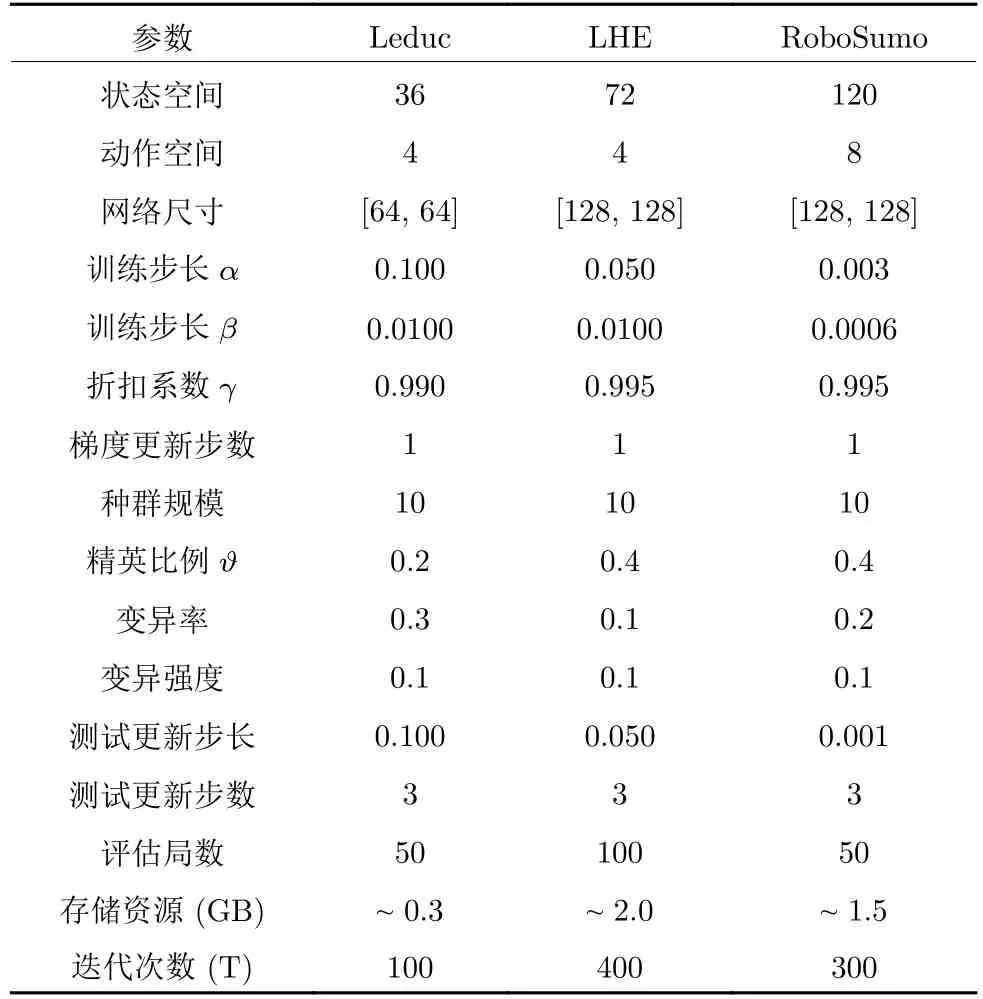
表1 不同环境下的实验参数设置Table 1 Hyperparameters settings

需要注意的是,适应过程中的各类对手都没有用于元模型的训练.同时,本文还提供了一系列涵盖不同风格以及不同实力的博弈对手,用于元模型和各类基线算法的公平对比.Leduc 扑克中各类对手具体包括: 1) Random 对手会随机采取各类动作,博弈水平相对较弱;2) Call 对手总是采取跟牌动作,具有明显的博弈风格;3) Bluff 对手会根据手牌强弱进行动作并在一定概率内进行诈唬,博弈水平接近人类玩家;4) CFR 对手是通过基线方法中的CFR 训练得到的,属于近似纳什均衡策略,很难被剥削;5) NFSP 对手是通过基线方法中的NFSP 算法训练得到的.在规模更大的两人有限注德州扑克LHE 中,本文提供了三类更加符合人类玩家特征的对手模型,分别为比较激进的LA 型对手,相对激进并有一定概率诈唬的TA 型对手,以及相对保守的LP 型对手.这三类对手策略基于专业牌手常用的德州扑克手牌计算器PokerStove 的缓存矩阵所计算出的获胜概率进行决策.因此这三类对手策略的博弈水平更加贴近真实人类玩家.RoboSumo 中的对手策略 A gentZooN(N=1,2,3) 为Bansal等[51]使用PPO 算法训练后开源的预训练模型,其中N的不同取值代表了训练时采用的不同随机种子.这三类开源的预训练对手模型的博弈水平较高且呈现出了不同博弈风格,已经被作为基线模型广泛使用[33].

如表2 所示,元模型在面对Leduc 扑克中各类风格的对手时,都表现出了快速的适应性.在面对实力较弱或者表现出明显博弈风格的对手 (比如Random、Call 等类型) 时,元模型可以快速更新到该类对手的近似最佳响应.在面对风格多变或者近似均衡这类很难去发现弱点进行剥削的对手时,元模型也可以快速提高对局中的平均收益.因此实验表明,通过结合元学习的策略更新方式,元模型在策略空间内更新到了拥有快速适应性的初始化区域,从而在面对未知风格对手时可以快速提升自身博弈水平.表3 展示了元模型在LHE 中也具有类似的快速适应性.图2 展示了适应后的元模型相比RoboSumo 中内置的基线算法的平均胜率,可以看出适应后的元模型相比于基线模型的胜率得到了大幅提升.

表2、表3 还展示了元模型与各类基线算法的实验对比情况.可以看出,元模型相比于对手建模类算法DRON和EOM,在同样的交互数据量以及更少的适应步骤 (三步梯度更新) 内获取了更高的平均收益.需要注意的是,本实验中的DRON和EOM 方法使用了与元模型相同的交互数据对对手进行建模,但是并没有对梯度更新步骤进行限制.这也与本文前面提到的对手建模类算法需要大量交互数据拟合相对准确的对手模型的特点相一致.此外,元模型相比于近似均衡类求解方法 (NFSP和CFR),在面对实力较弱的对手时能够大幅提升平均收益.而传统的元学习类MAML 算法仅在面对Random 类对手时具有快速适应性,这是由于MAML类算法在训练过程中缺乏高质量对手,仅依靠随机生成的对手进行训练,无法在参数空间内进行高效探索.

本文所提出的种群演化对手生成算法,正是通过选择、交叉、变异算子实现了兼顾难度与风格的对手自动生成.元模型通过不断与这些自动生成的对手进行训练,逐步提升了自身策略的适应性.第3.2.2 节对该对手生成模块的作用机制展开了详细实验验证.最后,与基线算法 “本文算法 +PPO”的实验结果对比也说明了本算法具有与模型无关(Model-agnostic) 的性质[32],可以与任何梯度优化算法兼容.

3.2.2 种群演化模块验证

本节主要针对第2.3 节中提出的种群演化对手生成算法的作用机制展开实验验证.主要包括: 1) 算法消融性实验;2) 演化自动生成的对手策略是否具有多样性;3) 超参数设置对实验性能的影响.

图3 展示了种群演化模块对元模型实验性能的影响,三条曲线代表了不同模型在Leduc 扑克中面对Random 对手的表现.“本文算法”代表本文所提算法;“本文算法 −EA”代表移除种群演化模块后,仅使用元模型更新算法;“EA 算法”代表仅使用种群演化算法来生成对手,不使用元模型的更新方式.

由图3 可以看出,元模型的更新方式和种群演化模块对于实验性能的提升都有显著作用.仅使用种群演化算法的EA 模型性能提升缓慢,而且方差比较大,这是因为进化算法更新过程中并不使用梯度信息,采样效率较低.当不使用种群演化模块时,元模型只能通过自博弈的方式进行策略更新,会导致元模型在参数空间内探索受限,泛化性较差.当同时使用元模型更新方式和种群演化算法时,模型的性能大幅提升,而且表现更加稳定.这是因为种群演化算法通过选择、交叉、变异算子的共同作用,自动生成了兼顾难度与风格的对手数据,从而提升了元模型的泛化性与适应性.同时,元模型通过与这些对手进行不断交互,提升了自身快速适应性.在Leduc 扑克、两人有限注德州扑克和RoboSumo中面对不同种类对手进行的消融实验,更加充分地验证了本文所提出的种群演化模块和元模型更新算法的有效性,具体实验结果见表2、表3和图2.

图4 可视化了种群演化算法自动生成的对手策略.这4 幅图分别对应Leduc 扑克环境下对手策略种群里4 个对手模型的动作概率分布.每幅图中的动作概率分布均由元模型与相应对手模型对打10 000局后统计得出.横坐标代表了Leduc 中的不同牌型,纵坐标代表了持有该牌型时各个动作的概率.图4下方的4 个图例分别代表了Leduc 中4 个不同的可选动作.从图4 中可以看出,自动生成的对手策略覆盖了更大的策略空间,而且由于选择、交叉、变异算子的共同作用,自动生成的对手策略并不仅仅关注策略上的差异性,还兼顾了模型的性能.例如,在拿到较强牌力的手牌时,弃牌的概率相应减小.

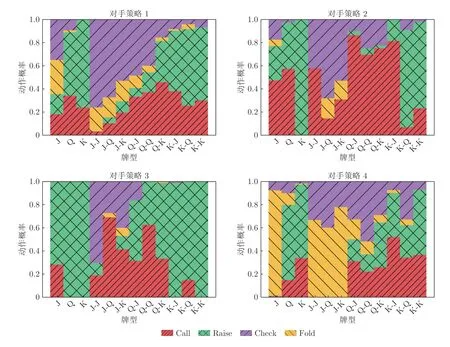
图4 种群演化模块生成的对手策略Fig.4 Visualization of the styles of the strategies

超参数的选择对实验性能也会造成一定影响,表1 中详细展示了通过网格搜索确定的一组超参数.其中,“评估局数”的设置会对实验性能产生较大影响.图5 显示了评估局数的不同取值对元模型性能的影响.当评估局数较少时,模型性能出现了剧烈震荡;随着评估局数的增加,模型的方差逐渐变小,性能也随之提升.这是因为该参数代表了对手生成模块中选择算子评估对手模型性能的对局数量,这直接影响了子代种群的模型性能.通过实验发现,评估局数较多时挑选出的子代种群有利于模型性能的提升,在本文的三类实验场景中,50～100是一个比较合理的范围,能够兼顾评估速度与质量.

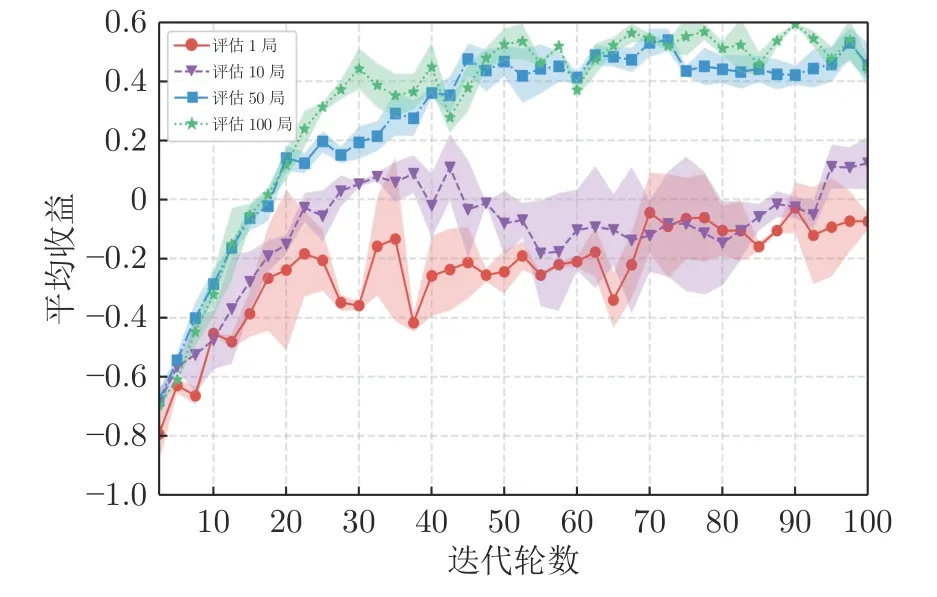
图5 超参数设置对模型性能影响Fig.5 Effect of hyperparameter settings

4 结论

本文提出了一种针对两人零和博弈的快速适应算法,该算法克服了均衡求解方法中策略过于保守以及对手建模方法泛化性差的弊端.本算法主要分为对手自动生成和元模型更新两个阶段.在对手生成阶段,通过种群演化算法中的选择、交叉和变异算子来自动生成兼具不同风格与博弈水平的对手策略.在元模型更新阶段,模型通过不断与这些对手进行交互并结合元学习的参数更新方式,来不断提升模型面对不同博弈对手的泛化能力.

在Leduc 扑克、LHE 以及RoboSumo 中的实验结果表明,本文算法在与对手进行少量交互的情况下,使用同一个元模型针对不同风格的对手都实现了快速适应.相比于均衡类算法,本文算法能够实现对次优对手的剥削;相比于对手建模类算法,本文算法避免了显式建模过程,提高了模型的泛化能力.消融实验与可视化实验的结果显示了本文算法所使用的对手演化生成模块与元模型更新算法的有效性.如何将本文算法应用到更大规模的游戏(例如,无限注德州扑克)以及如何结合均衡类算法的优点来保证元模型在适应过程中的安全性,是本文未来可以继续研究的方向.