GNSS 静态相对定位精度分析与比较

符宏伟

（上海市测绘院，上海 200063）

0 引言

2020 年6 月，随着北斗卫星导航系统（BeiDou navigation satellite system, BDS）第55 颗卫星成功发射，我国第三代北斗卫星导航系统即北斗三号（BeiDou navigation satellite system with global coverage, BDS-3）全部星座部署完成，全球卫星导航系统（global navigation satellite system, GNSS）得到大力发展和完善。目前，GNSS 由全球定位系统（global positioning system, GPS）、BDS、格洛纳斯卫星导航系统（global navigation satellite system,GLONASS）、伽利略卫星导航系统（Galileo navigation satellite system, Galileo）等组成[1]。随着各卫星系统的完善，GNSS 在气象学、工程测量学、精准农业等各个领域得到了广泛应用，这对GNSS的基线解算都提出了更高的要求[2-5]。

GNSS 常用的定位方式有静态相对定位、实时动态差分、精密单点定位、实时广域差分等方式，静态相对定位的精度最高，在长距离和短距离GNSS基线解算中，一般都能获得满意的定位结果[6]。伽米特（GAMIT）/格洛博克（GLOBK）是由麻省理工学院（Massachusetts Institute of Technology, MIT）开发的高精度GNSS 数据后处理软件，从GAMIT 10.61 版以来，不仅支持GPS 数据的处理，还能够单独解算BDS、GLONASS、Galileo 等其他卫星导航系统的观测数据。目前，GAMIT/GLOBK 的最新版本为10.71。文献[7-9]基于GAMIT 软件分析和比较了BDS 基线和GPS 基线的解算精度，解算结果表明，BDS 基线解算在北（N）、东（E）、高（U）方向的精度都比 GPS 精度低。文献[10]基于GAMIT 的不同解算策略，解算了BDS 短基线和长基线，初步评估了BDS 用于精密相对定位的可靠性和精度。文献[11]解算了BDS 短基线，结果表明BDS 短基线解算精度在厘米级。以上研究较为单一，没有分别对长基线和短基线进行分析，卫星导航系统之间也没有进行相互比较。

本文选取6 个多模GNSS 跟踪网（multi-GNSS experiment, MGEX）测站的观测数据组成的长基线以及城市四等实测短基线，利用GAMIT 10.71 分别解算GPS、BDS、GLONASS、Galileo 的基线，短基线实测网还进行网平差计算，以此分析和比较各卫星导航系统长短基线的解算精度。

1 基线质量评价指标[12-14]

1.1 标准化均方根误差

标准化均方根误差（normalized root mean square, NRMS）sNRMS是衡量GAMIT 基线解算质量的重要指标之一，它体现了单时段基线解算值与其加权平均值的偏离程度。一般情况下sNRMS小于0.3，如果sNRMS大于0.5，那么说明该时段的基线结果解算不合格。sNRMS的计算公式为

式中：N为测站个数；iY、Y分别为基线解算值和其加权平均值；iδ为单位权中误差。

1.2 基线重复性

重复性是衡量GNSS 基线质量的重要指标之一，它体现了基线结果的离散程度。基线重复率体现了基线的内符合精度，基线重复率值越小，内符合精度越高，基线精度越高；基线重复率越大，内符合精度越低，基线精度越低。

GNSS 单天解基线的N分量、E分量、U分量及基线长（L）分量的重复性检验的计算公式为

式中：Lk为基线长度；a为常系数；b为与基线长度成比例的系数。

1.3 基线中误差

基线中误差是评定基线分量精度的一个指标。在GAMIT 解算结果文件中，包含了各条基线在N、E、U及L方向上的基线分量中误差。该误差反映了基线解质量的高低，其数值越小，基线解精度越高；其数值越大，基线解精度越低。

2 算例与分析

2.1 长基线相对定位

选取中国境内的武汉站（WUH2）、乌鲁木齐站（URUM）、香港屯门站（HKSL）、香港黄石站（HKWS）、武汉九峰站（JFNG）、拉萨站（LHAZ）等6 个MGEX 站2020 年年积日第121—149 天的观测数据，利用GAMIT 10.71 分别解算GPS、BDS、GLONASS、Galileo 组成的基线。解算过程中：最短基线为JFNG 和WUH2 间的基线，基线长约为12.961 km；最长基线为HKWS 和URUM 间的基线，基线长约为3 371.996 km，基线平均约长为609.042 km。除HKSL 和HKWS 间的基线和JFNG和WUH2 间的基线为中长基线，其余基线均为长基线。文献[15]分析了GAMIT 解算时不同参数对BDS 长基线精度的影响，结果表明，卫星高度截止角和测站约束值对基线解算精度有较大影响，而对流层天顶延迟参数个数对基线精度影响较小。文献[13]分析和对比了GAMIT 不同的解算模式，研究表明长基线解算中 BASELINE 模式精度较好。因此，本文在长基线解算时，GAMIT 进行如下参数设置：数据采样间隔设置为30 s；卫星高度角设置为10°；测站约束设置为0.05 m、0.05 m、0.05 m；观测值选择（Choice of Observable）为LC_AUTCLN；解算策略（Choice of Experiment）为BASELINE；分析类型（Type of Analysis）为1-ITER；电离层模型（Ion model）为高阶电离层延迟模型（GMAP）；全球海潮模型（otl.grid）为FES2004；广播星历采用混合广播星历；精密星历采用德国地学研究中心（Deutsche Geo Forschungs Zentrum, GFZ）计算的混合精密星历。各卫星导航系统基线解算的sNRMS结果见图1。

由图1 可知，四大卫星导航系统解算的sNRMS都低于0.3，表示所有时段的数据都解算成功。GPS解算的sNRMS最小，平均为0.216，表明GPS 的基线值偏离其加权平均值的程度最小，Galileo 解算的sNRMS最大，平均为0.256，表明Galileo 的基线值偏离其加权平均值的程度最大，BDS 和GLONASS 解算的sNRMS平均值分别为0.223 和0.228。

图1 长基线 sN RMS 统计

为了作图简洁，将6 个MEGX 站组成的15 条独立基线编号，使基线名称和基线序号一一对应。对应关系为表1。

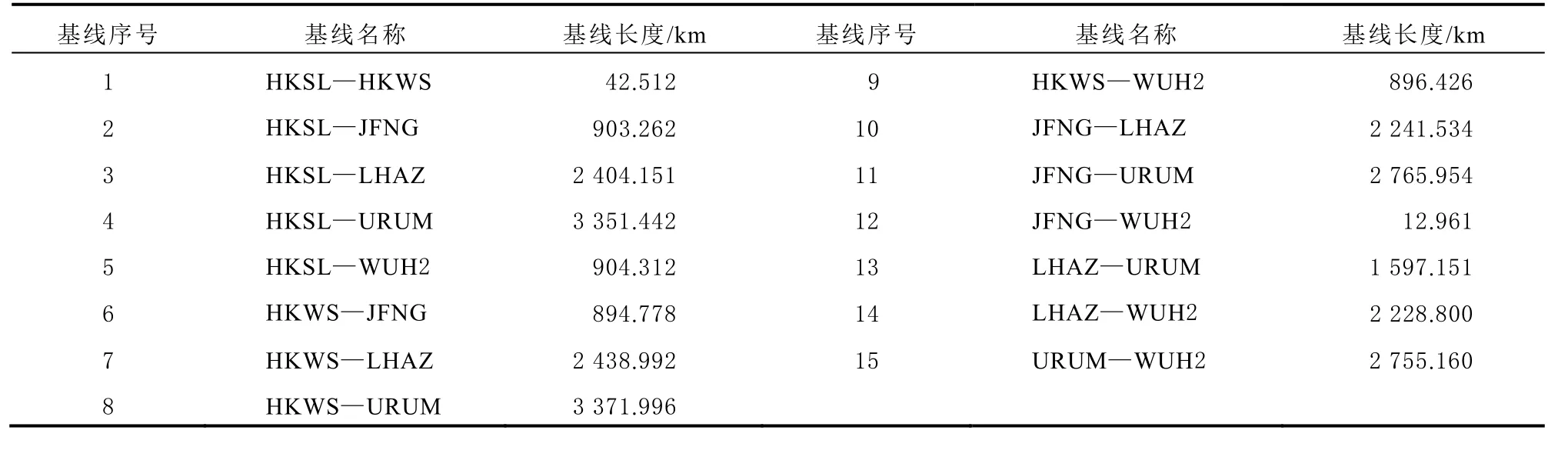
表1 基线序号与基线名称的对应关系表

将各基线的基线中误差取平均值，得到各基线的基线中误差平均值，相关结果见图2。

图2 各基线N、E、U 及L 方向基线中误差平均值统计图

由图2 可知，四大卫星导航系统U方向的基线中误差最大，BDSN、E、U方向和L上的基线中误差最大且波动最大，GPSN、E、U方向和L上的基线中误差最小且波动最小，GLONASS 和Galileo 基线中误差较相近。将各基线中误差平均值取平均值，得到GPS、BDS、GLONASS、Galileo的基线在N、E、U及L方向的中误差分别为（2.2 mm，2.2 mm，8.0 mm，2.2 mm）、（7.5 mm，12.7 mm，42.6 mm，13.1 mm）、（3.5 mm，5.5 mm，12.4 mm，4.6 mm）、（3.6 mm，4.1 mm，12.2 mm，3.4 mm）。

通过最小二乘拟合得到基线重复性的常数部分和比例部分的值，计算结果见表2。

表2 基线重复性常数部分和比例部分统计表

由表2 可知，四大GNSS 系统的基线重复性都较好，无论是固定误差还是比例误差，U方向精度均低于N、E和L方向的精度。BDS 系统N、E、U方向的固定误差比其他系统相应的固定误差大，U方向固定误差为2 cm 左右。GPS 水平方向比例误差优于6×10-10，其他卫星导航系统优于3×10-9；垂直方向除 BDS 外，其他卫星导航系统都优于5×10-9；基线长方向比例误差GPS 优于5×10-10、Galileo 优于9×10-10、BDS 优于7×10-10、 GLONASS优于2×10-9。

2.2 短基线相对定位

选取两个实测的短基线控制网，先利用GAMIT软件分别解算各卫星导航系统组成的基线，然后利用科傻GPS（CosaGPS）进行网平差计算，从最弱边精度以及平差后的点位坐标进行比较分析。短基线控制网1 有两个已知点，分别为C3C3 和G7G7；有7 个未知点，分别为C1C1、C2C2、C9C9、C7C7、C5C5、 CC10、G6G6；最短基线为C9C9和CC10 间的基线，基线长约为321 m；最长基线为C3C3 和G6G6 间的基线，基线长约为5 000 m；平均基线长约为2 199 m。控制网2 有两个已知点，分别为G1G1 和G8G8；有5 个未知点，分别为G11A，G3G3、G6G6、G7G7、G9G9；最短基线为G7G7和G8G8 间的基线，基线长约为471 m；最长基线为G1G1 和G8G8 间的基线，基线长约为5 516 m；平均基线长约为2 699 m。两个控制网观测等级为城市四等网，最弱边相对中误差不得低于1/45 000。控制网的网型示意图见图3 和图4。

图3 工程短基线控制网1 示意

图4 工程短基线控制网2 示意

文献[16]研究了GAMIT 在解算GPS 短基线时，不同的基线解算类型对解算精度的影响，结果表明，对于双频 GPS 接收机，短基线宜采用L1,L2_INDEPEND 的解模式。因此，本文短基线解算时，GAMIT 解算模式设置为L1,L2_INDEPEND，测站约束设为100 m,100 m,100 m，其余参数与长基线解算时的参数一致。两个控制网各系统基线解算sNRMS值见表3，平差后的最弱边相对中误差计算结果见表4。

表3 两个控制网四大卫星导航系统基线解算 sNRMS值

由表3 可知，两个控制网各卫星导航系统解算得到的sNRMS都小于0.5，说明基线解算合格，两个控制网均是GPS 的sNRMS值最小，GLONASS 的sNRMS最大。

从表4 可知，两个控制网各GNSS 网平差得到的最弱边相对中误差都满足城市四等网的要求；控制网1 最弱边不为同一条边，控制网2 的最弱边为同一条边，且都不是GPS 的最弱边精度最高，原因可能是GNSS 数据质量与测站位置和测站环境有关。

表4 各GNSS 系统最弱边相对中误差

两个基线网通过解算GPS 的基线后，平差得到的未知点坐标与通过网络RTK 得到的点位坐标差值都在1 cm 内，所以将GPS 平差得到的点位坐标作为参考值，其他卫星导航系统平差得到的点位坐标与GPS 的点位坐标差值见图5。

图5 两个控制网平差后的点位坐标和GPS 解算的差值

除控制网1 的C5C5 点位X方向GLONASS的计算结果与GPS 的差值约为1 cm，Y方向Galileo和GLONASS 的计算结果与GPS 的差值约为1.5 和2 cm 外，其余各点位各系统与GPS 的差值均在1 cm 内，说明在城市四等短基线控制网中，各GNSS 系统单独解算均能满足要求。

3 结束语

本文基于GAMIT 10.71 结合MGEX 站组成的长基线和城市四等短基线实测数据，分析和比较了GPS、BDS、GLONASS、Galileo 的相对定位精度，可以得到如下结论：

1）长基线sNRMS的计算结果表明，不同系统单独解算sNRMS都小于0.3，其中GPS 的sNRMS值最小，Galileo 的sNRMS最大，表明GPS 的基线值偏离其加权平均值的程度最小，Galileo 的基线值偏离其加权平均值的程度最大。

2）长基线基线重复性的计算结果表明，BDS的固定误差最大，其他卫星导航系统的固定误差比较接近，四大卫星导航系统比例误差在水平方向优于3×10-9，垂直方向优于2×10-8，基线长方向精度优于7×10-9，相对而言GPS 的相对误差最小，水平方向和基线长方向可达到6×10-10，垂直方向精度可达到2×10-9。

3）长基线基线中误差的计算结果表明，BDS在N、E、U和L方向上的基线中误差最大且波动最大，GPS 在N、E、U和L方向的基线中误差最小且波动最小，GLONASS 和Galileo 的基线中误差较相近。

4）短基线平差后的精度表明，在城市四等控制网中，各GNSS 独立解算都能满足最弱边相对精度，且平差后的点位坐标绝大多数与GPS 的差值在1 cm 内，说明平差结果可靠。

通过对GPS、BDS、GLONASS、Galileo 的长短基线解算与分析，表明各卫星导航系统都能满足相对定位的需求，为各系统单独用于工程实践提供了参考。