基于全球MGEX 观测站的BDS 卫星精密定轨研究

李鹏杰，张捍卫

（1. 河南理工大学 测绘与国土信息学院，河南 焦作 454003；2. 河南理工大学 资源与环境学院，河南 焦作 454003）

0 引言

第三代北斗卫星导航系统即北斗三号（BeiDou navigation satellite system with global coverage, BDS-3）于2016 年开始建设，卫星星座由30 颗在轨卫星构成[1]。截至2020 年7 月，BDS-3星座部署全面完成并向全球用户提供服务。BDS-3星座由24 颗中圆地球轨道（medium Earth orbit,MEO）卫星、3 颗倾斜地球同步轨道（inclined geosynchronous orbit, IGSO）卫星和3 颗地球静止轨道（geostationary Earth orbit, GEO）卫星构成。在3 颗GEO 卫星中，2 颗GEO 卫星处于在轨服务状态，1 颗GEO 卫星处于在轨测试状态。精密轨道作为导航卫星的核心产品，是其他科学研究和导航定位授时服务的基础[2]，北斗卫星导航系统（BeiDou navigation satellite system, BDS）也是目前能够为全世界提供服务的全球卫星导航系统（global navigation satellite system, GNSS）之一。

在BDS 精密定轨方面，文献[3-4]分别针对BDS 单系统定轨和全球定位系统（ global positioning system, GPS）辅助BDS 定轨的联合定轨法进行了研究，指出GPS 辅助BDS 定轨的联合定轨法，可使BDS 卫星定轨精度有显著提升。文献[5]利用区域观测站数据，对影响轨道精度和实时性的5个要素（模糊度固定、测站数量、定轨弧长、光压模型和多系统联合定轨）进行了分析，给出了利用区域观测站进行BDS 卫星定轨的优选方案。文献[6]提出了基于超快速精密轨道约束的实时滤波定轨方法，并采用BDS 观测数据，进行了精密定轨验证。文献[7]利用区域观测站数据和星间链路观测技术，进行了BDS 卫星精密定轨，得到重叠弧段轨道3 维均方根（3D root mean square,3D-RMS）为15.4 cm，24 h 的轨道预报位置精度为20.3 cm。文献[8-9]采用BDS 卫星不同频率的组合观测值，验证了不同观测值类型对轨道精度的影响。文献[10]选取16 个地面观测站的BDS 观测数据，进行了 BDS-3 卫星数据质量分析以及BDS 单系统定轨。上述研究主要针对的是卫星单天弧段轨道的精密确定。由于单天弧段轨道存在末端效应，通常将单天弧段轨道合成多天弧段轨道以提高定轨精度[11]。多天弧段轨道的合成，不同弧段长度的选择，将直接影响数据计算效率和定轨精度。文献[12]利用实测数据验证了不同因素（例如测站分布、数量，定轨弧段等）对卫星精密定轨的影响。文献[13]基于卡尔曼（Kalman）滤波原理，研究了不同单天弧段解的合成。

由于多模GNSS 试验（multi-GNSS experiment，MGEX ） 网 和 国 际 GNSS 监 测 评 估 系 统（ international GNSS monitoring & assessment system, iGMAS）的 BDS 观测数据有限且测站分布不均匀，现有研究一般采用区域观测数据，通过BDS/GPS 联合定轨方法来确定BDS 卫星轨道。而利用全球观测站确定BDS 卫星轨道的相关研究则相对较少。本文利用全球MGEX 观测站数据，对目前导航卫星定轨中常用的3、5 和7 d 弧段长度定轨方案进行精密定轨研究。通过对不同定轨方案所得的卫星轨道进行比较分析，最后得出了利用全球MGEX 观测站数据确定BDS 卫星轨道定轨弧段长度的优选方案。

1 基本原理

导航卫星精密定轨是利用伪距和相位观测量求解卫星轨道参数，对所得轨道参数进行积分得到单天弧段卫星轨道。为了克服单天弧段轨道末端效应对轨道精度的影响，需要将不同单天弧段轨道合成多天弧段轨道，以提高多天弧段轨道中间部分的轨道精度。下面将分别对单天弧段轨道确定和轨道合成进行讨论。

1.1 单天弧段轨道确定

设BDS 卫星的运动方程[6]为

式中：x(t) 为t时刻相对于状态向量初始值的改正数向量；x(t0)为t0时刻相对于状态向量初始值的改正数向量；Φ(t0,t)为状态转移矩阵；0w为系统噪声向量。

利用BDS 观测方程和观测模型，建立观测量与状态向量之间的函数关系，求解BDS 卫星轨道状态参数。设观测向量Y与状态向量X的函数关系为Y=G(X,t)+ε。将其进行线性化后得到观测方程[14]为

1.2 多天弧段轨道合成

通常GNSS 精密定轨一次只能处理一天的观测数据，得到卫星单天弧段轨道。本文依据Kalman滤波原理，实现多天弧段轨道合成，其具体实现过程是：通过Kalman 滤波实现单天弧段轨道的法方程叠加，求解测站坐标、卫星轨道参数和地球定向参数的最佳估值，可分为时间更新和状态更新两个步骤[15]：

1）时间更新

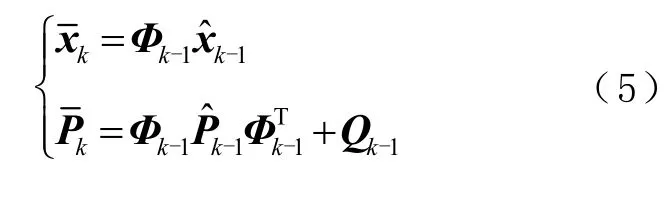
2）状态更新

2 定轨策略

本文基于加米特（GAMIT）软件包，实现了BDS 精密定轨。对每一天的BDS 观测数据处理策略是：采用双差方法处理观测数据；采用“一步法”同时求解卫星轨道参数、卫星钟差、对流层延迟参数、地球定向参数和测站坐标等[8]，具体解算策略和模型见表1。

表1 BDS 卫星定轨动力学模型及参数设置

对于单天弧段解（h 文件）合成，获取中间1 d 卫星轨道的原理。如图1 所示，由连续3 d 的BDS 观测数据确定中间1 d 卫星轨道方法为：首先利用中间1 d（Day2）的预报轨道和BDS 观测数据，获取BDS 卫星轨道参数（g 文件）；然后以中间1 d 的卫星轨道参数为基础，处理前后2 d（Day1和Day3）的BDS 观测数据，得到单天弧段解，通过Kalman 滤波合并3 个单天弧段解，获取合并后的轨道参数进行轨道积分；最后截取中间弧段长度为1 d 的轨道作为定轨结果。该方法可使定轨弧段中间部分轨道精度，优于相应单天弧段轨道精度[17]。

图1 轨道合成示意

3 数据来源

选取全球均匀分布的80 个MGEX 观测站，2020 年年积日第86—93 天的BDS 观测数据进行定轨实验，获取BDS 卫星精密轨道。测站分布如图2所示。其图2 中，五角星代表观测站位置。

图2 MGEX 观测站分布【审图号：GS（2021）5770 号】

观测数据质量好坏直接影响到卫星精密定轨的精度。本文基于格-纳特（G-Nut）/阿努比斯（Anubis）软件，对上述选取的80 个全球均匀分布的MGEX 观测站连续8 d 的BDS 观测数据，从数据可用率和周跳方面进行数据质量评估，其分析结果如图3 所示。其中，数据可用率Rua[18]为

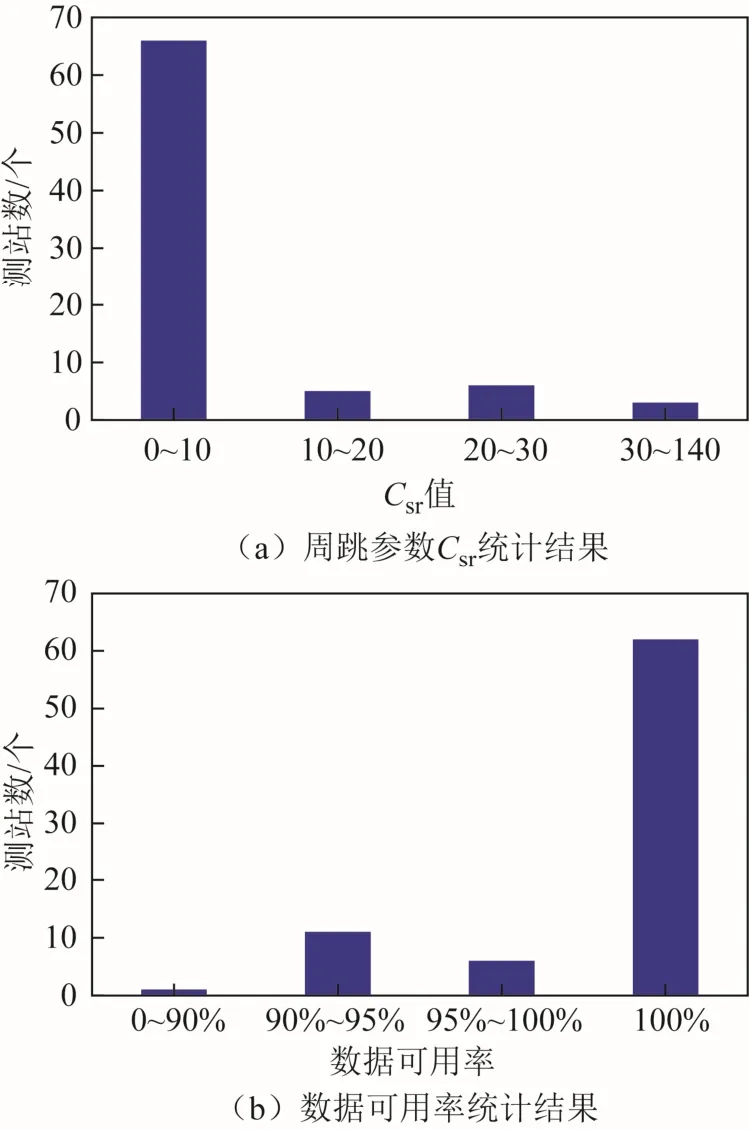
图3 MGEX 测站BDS 观测数据质量分析

由图3（MGEX 测站BDS 观测数据质量统计结果）可得，参与数据质量评估的80 个MGEX 观测站，连续12 d 观测数据周跳参数Csr均值小于10且数据可用率Rua值大于95%的测站个数占总测站数的82%以上。除去个别数据质量较差的测站，其余测站数据均能满足精密定轨要求。

4 结果分析

为了验证3 种方案的定轨精度，以武汉大学国际GNSS 服务组织（International GNSS Service, IGS）数据中心提供的混合精密轨道为基准，将定轨结果与精密轨道进行比较，得到各颗卫星在轨道径向（R）、横向（A）、法向（C）和3 维（3D）的精度（RMS）。通过BDS 轨道位置分量平均误差即1 维RMS（1D-RMS）来评价BDS 系统整体的定轨精度。

4.1 BDS MEO 和IGSO 卫星定轨精度

文中采用3 种方案进行BDS 精密定轨，3 种方案都采用双差法进行数据处理，基本的处理策略相同，仅在定轨弧段长度上有所区别，如图4 所示。此外，本文对各方案的计算时间进行了统计，定轨计算在云服务器上进行，服务器的配置为双核中央处理器（central processing unit, CPU），4.00 GB内存，乌本图（Ubuntu）16.04 操作系统。

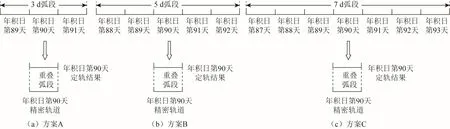
图4 3 种定轨方案示意

各颗卫星的定轨精度如图5、图6 所示，其中，图5 为BDS GEO 卫星定轨精度，图6（a）至图6（d）分别为BDS MEO 和IGSO 卫星为径向、横向、法向和3 维的定轨精度；表2 给出了各方案的计算时间及BDS 轨道的1D-RMS 统计结果；表3 为BDS MEO 和IGSO 卫星3 种方案定轨精度统计结果。

表2 各方案计算时间及BDS 轨道的1D-RMS 统计结果

图5 BDS GEO 卫星轨道精度

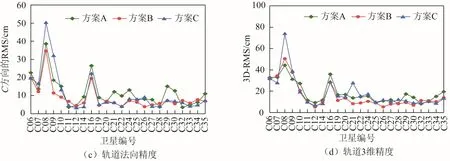
图6 BDS MEO 和IGSO 卫星3 种方案的定轨精度

由表2 和表3 的统计结果可以得出，各方案定轨结果的3 维精度均值都优于20 cm，方案A 定轨结果的3 维精度为18.27 cm，方案B 定轨结果的3 维精度15.51 cm，方案C 定轨结果的3 维精度为18.13 cm。方案B 定轨结果较好，但相比方案A 需更多的计算时间。这充分说明BDS 卫星的定轨精度并非随着定轨弧段长度增加而改善，同时定轨弧段长度的增加，使得法方程规模急剧增大，需要消耗大量的计算机硬件资源和计算时间。对于 MEO 卫星，3 种方案各颗卫星的轨道径向精度基本相当，横向精度和法向精度波动较大。对于IGSO 卫星，3 种方案定轨结果的精度都低于MEO卫星定轨结果的精度。这是因为采用全球范围的MGEX 观测站，对MEO 卫星的观测弧长进一步增加，使得MEO 卫星定轨精度显著高于IGSO 卫星定轨精度。由于GEO 卫星相对“静止”的轨道特性，造成多数MGEX 测站无法对其进行有效观测，所以GEO 卫星的定轨精度明显更低。相比径向精度定轨弧段长度的变化，对IGSO 和MEO 卫星轨道横向精度和法向精度影响更明显。造成此现象的原因是：卫星轨道动力学模型多数是针对径向力建模，对轨道横向和法向力建模相对较少，故随着轨道弧段长度的变化，横向精度和法向精度变化相比径向精度更为显著。另外，从有/无GEO 卫星加入定轨计算，得出加入GEO 卫星进行定轨计算，会增加计算时间，也会使BDS 系统整体的定轨精度降低。

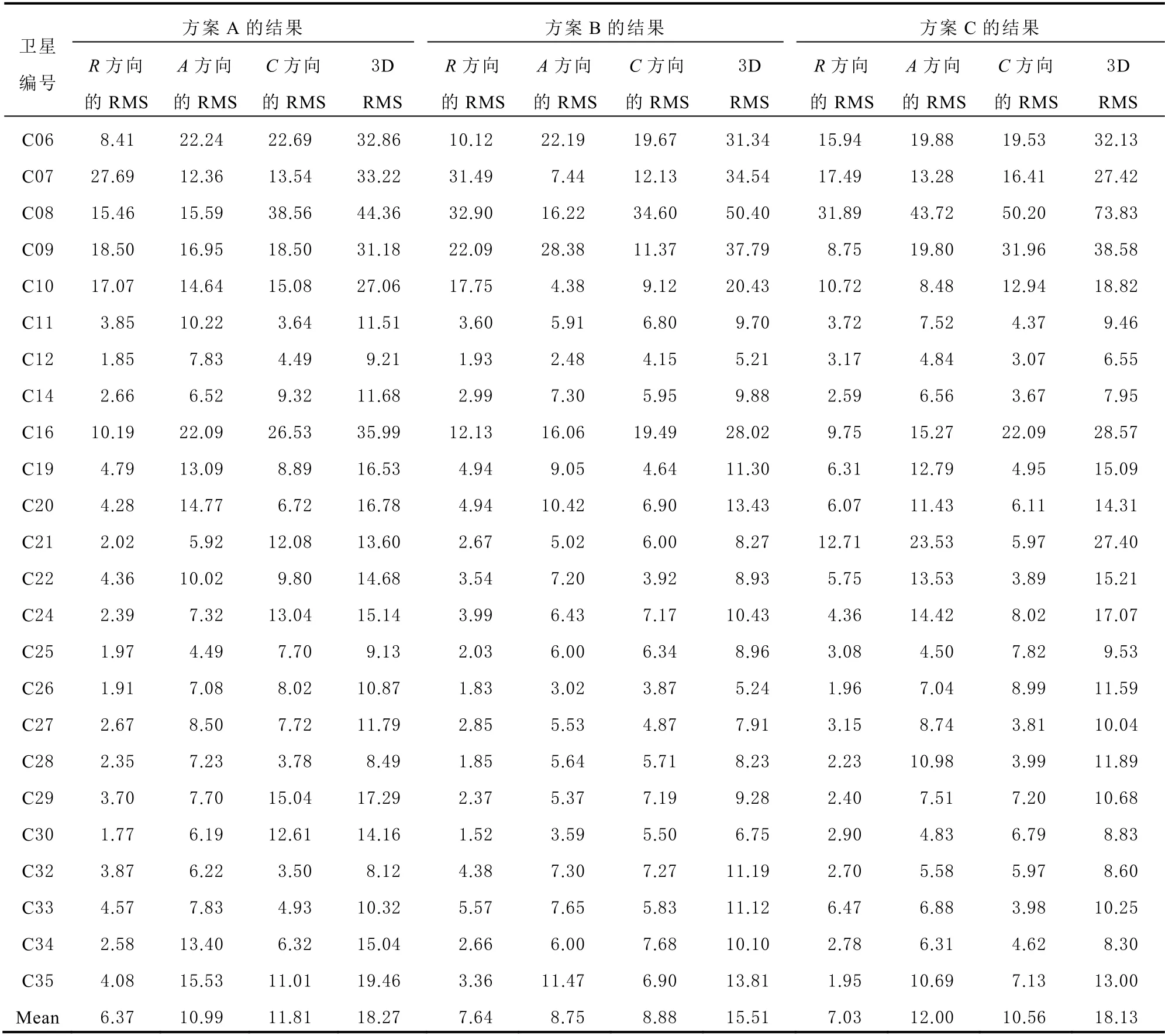
表3 BDS MEO 和IGSO 卫星3 种方案定轨精度统计结果 单位：cm

4.2 轨道预报精度

轨道预报比较是重要的定轨精度检验手段。如图7 所示，轨道预报过程主要包括：1）采用各方案定轨结果拟合轨道参数；2）利用拟合的轨道参数进行积分，得到拟合轨道和预报轨道。通过轨道预报与相应的精密轨道形成重叠弧段，进而得到预报轨道径向、横向、法向和3 维的精度。表4 详细列出了各方案拟合弧段长度、积分弧段长度和预报72 h 的年积日序号。对上文各方案轨道预报72 h，限于篇幅限制仅统计C08、C13、C14、C20、C21、C25、C26、C28 和C29 卫星的预报精度，其结果如图8 所示。其中，图8（a）为方案A 轨道预报结果；图8（b）为方案B 轨道预报结果；图8（c）为方案C 轨道预报结果；Mean 为平均值。

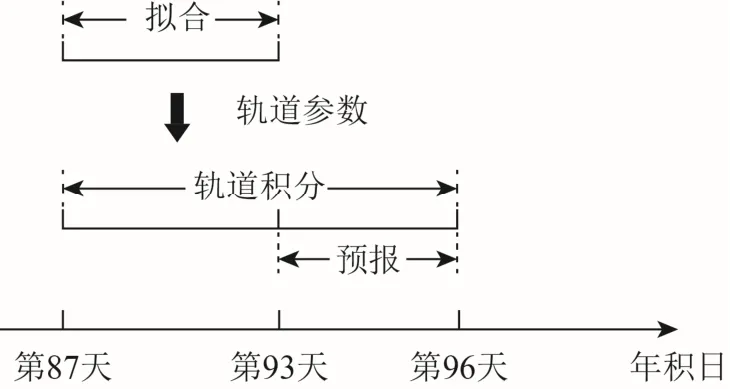
图7 轨道预报原理

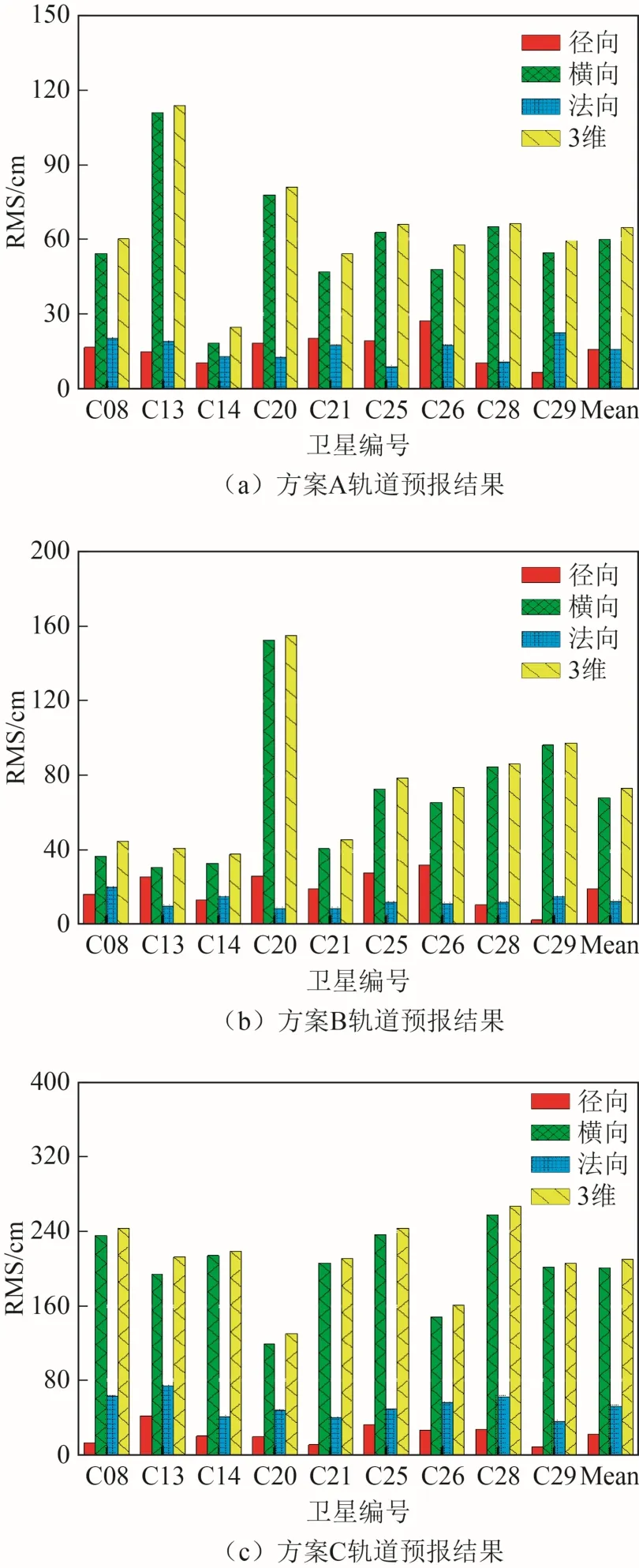
图8 预报72 h 轨道精度

表4 BDS MEO 和IGSO 卫星轨道预报方案

由表5 给出预报72 h 轨道精度统计结果，由表5 可得：

表5 预报至第72 h 的轨道精度统计结果 单位：cm

1）方案A 轨道预报72 h，径向精度为16.0 cm，横向精度为59.8 cm，法向精度为15.7 cm，3 维精度为64.8 cm。

2）相比方案B 和方案C，方案A 轨道预报72 h，在径向和横向上的精度优于方案B 和方案C轨道预报精度。其中，3 种方案轨道预报72 h，径向和法向的精度均优于横向精度。

5 结束语

BDS 卫星定轨精度取决于轨道动力学模型和几何观测量精度，由于轨道积分方法的局限性，造成单天弧段轨道两端误差相对较大，且各天弧段轨道间不连续等问题。本文依据单天弧段轨道确定和多天弧段轨道合成的基本原理，采用双差方法进行BDS 卫星精密定轨，研究定轨弧段长度对BDS 卫星定轨精度的影响。所得结论如下：

1）利用MGEX 观测站进行BDS 卫星精密定轨，多天弧段解轨道合成不仅能够保持各天轨道间的连续性，更能显著地提高多天弧段轨道中间部分的轨道精度。然而，定轨弧段长度增加到一定限度，对轨道精度的改善作用将不再显著；同时对规模庞大的法方程求解，需消耗大量的计算机硬件资源与时间，严重影响了精密定轨数据处理效率。3 d 弧段定轨方案，可以取得数据量、计算量和定轨精度之间的平衡，获得最优的定轨结果。

2）由于BDS GEO 卫星的轨道特性和轨道动力学模型的缺陷，导致其在轨道径向、横向和法向3 个方向上定轨误差较大。在BDS 单系统定轨中，可考虑排除GEO 卫星以提高BDS 系统整体的定轨精度，减少运算时间。