一种带形状参数的球域Bézier曲线

丁 格，李军成，刘成志

(湖南人文科技学院数学与金融学院，417000，湖南，娄底)

0 引言

Bézier曲线[1]作为一种几何造型工具，以表示简单、使用灵活的特点被广泛地应用于CAD、CAGD、CG等领域。但众所周知，自然界中的任何物体都有厚度，而利用没有厚度的Bézier曲线进行几何造型仅仅是数学上的一种抽象或简化。若把Bézier曲线的控制顶点换成球域，可得到球域Bézier曲线[2]。从几何上看，球域Bézier曲线可视为具有可变厚度的空间Bézier曲线。因此，球域Bézier曲线可用于构造自然界中广泛存在的管状物体[3]。由于球域Bézier曲线与空间Bézier曲线的方程结构相似，故Bézier曲线的诸多算法可推广到球域Bézier曲线，如球域Bézier曲线的拼接[4]，球域Bézier曲线的升阶[5]，球域Bézier曲线拟合散乱数据[6]，球域Bézier曲线的能量极小化[7]等。

在利用球域Bézier曲线构造实体时，有时需要调整其形状以满足造型的需要。然而，当控制球保持固定时，球域Bézier曲线的形状将无法调整，这为球域Bézier曲线在实体造型中的应用带来了不便。在几何造型中，为了解决传统Bézier曲线形状不易调整的问题，许多学者构造了带形状参数的Bézier曲线，例如，基于三角函数构造的C-Bézier曲线[8]与拟五次三角Bézier曲线[9]、基于双曲函数构造的H-Bézier曲线[10]、同次扩展的Bézier曲线[11]、升阶扩展的Bézier曲线[12, 13]。这些带有形状参数的曲线在控制顶点保持不变的情形下可通过修改所含参数的取值对其形状进行自由调整。既然球域Bézier曲线是通过将Bézier曲线的控制顶点换成球域而得到，那么很自然地想到可将这些带形状参数Bézier曲线的控制顶点换成球域，从而得到相应带形状参数的球域Bézier曲线。为此，本文将α-Bézier曲线的控制顶点换成球域，构造出一种带形状参数的球域Bézier曲线，从而在控制顶球保持不变的情形下通过修改所含参数的取值实现对其形状的自由调整。

1 α-BBC的定义

给定球心为点pi(xi,yi,zi)半径为ri的控制球〈pi;ri〉(i=0,1,…,n)，n次球域Bézier曲线可表示为[2]

(1)

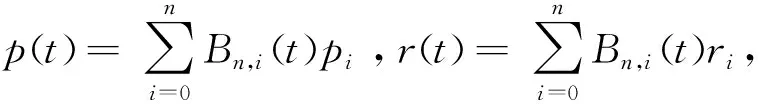
因此，球域Bézier曲线可视为由骨架pn(t)与半径函数rn(t)构成的具有可变厚度的曲线，如图1所示。

(a)三次球域Bézier曲线 (b) 四次球域Bézier曲线图1 球域Bézier曲线

不难可知，当控制球保持不变时，球域Bézier曲线也将随之固定，这在一定程度上限制了球域Bézier曲线的应用。为解决这一问题，可将式(1)中的Bernstein基函数替换为某种含自由参数的基函数，从而构造出带自由参数的球域Bézier曲线，在控制球保持固定时通过修改自由参数的取值实现对球Bézier曲线的形状调整。由于通过同次扩展所构造的α-Bernstein基函数[11]不仅含有1个自由参数，而且与传统Bernstein基函数相比，其方程结构的复杂度并未明显提高，故下面选取α-Bernstein基函数替换式(1)中的Bernstein基函数，构造出带参数α的球域Bézier曲线。首先给出α-Bernstein基函数的定义。

定义1[11]：设0≤t≤1，0<α≤1，称关于t的多项式

(2)

为三次α-Bernstein基函数，其中0<α≤1。进一步，称

gn,i(α;t)=(1-t)gn-1,i(α;t)+tgn-1,i-1(α;t)，i=0,1,…,n

(3)

为n(n≥4)次α-Bernstein基函数。

基于式(2)与式(3)表示的n(n≥3)次α-Bernstein基函数，可定义对应带参数α的球域Bézier曲线。

定义2：设0≤t≤1，给定球心为点pi(xi,yi,zi)半径为ri的控制球〈pi;ri〉(i=0,1,…,n)，称

(4)

为n(n≥3)次带参数α的球域Bézier曲线，简称为α-BBC，其中gn,i(α;t)(i=0,1,…,n)为式(2)与式(3)表示的α-Bernstein基函数。

注1：由于当α=1时式(2)与式(3)表示的α-Bernstein基函数即为Bernstein基函数[1]，故由式(4)不难可知，当α=1时α-BBC即为式(1)表示的球域Bézier曲线。因此，α-BBC是传统球域Bézier曲线的一种扩展。

2 α-BBC的性质

为方便讨论，不妨记Qi=〈pi;ri〉，于是式(4)可改写为

(5)

因此，α-BBC也可视为将α-Bézier曲线[11]的控制顶点替换为控制球而定义。根据α-Bézier曲线的性质，可得α-BBC的性质。

定理1：由式(5)表示的α-BBC具有如下性质。

1)对称性：分别由控制球Qn-i(i=0,1,…,n)与控制球Qi(i=0,1,…,n)定义的α-BBC相同，但参数化方向相反，即

〈G〉(α;t;Q0,Q1,…,Qn)=〈G〉(α;1-t;Qn,Qn-1,…,Q0)

(6)

2)端点性：α-BBC在两端点处满足

(7)

3)几何不变性：α-BBC的形状仅依赖于控制球与参数α的取值，而与坐标系的选取无关，即在控制球与参数α保持不变时，α-BBC的形状经过旋转、坐标系平移、按比例伸缩等几何变换后保持不变。

4)形状可调性：当控制球保持固定时，参数α取不同值将得到不同形状的α-BBC，即可通过修改α的取值实现对α-BBC的形状调整。

证明：1) 由式(2)与式(3)经简单计算可得gn,i(α;t)=gn,n-i(α;1-t)。于是，由式(5)有

此即表明式(6)成立。

2)由式(2)与式(3)经计算可得

于是，由式(5)经计算可得式(7)成立。

3)由于α-BBC可看作是将对应α-Bézier曲线中的控制顶点替换为控制球，故α-Bézier曲线满足的几何不变性同样也适用于α-BBC。

4)由于α-BBC的表达式中含有参数α，故在控制球保持不变的情形下，修改参数α的取值显然会改变α-BBC的形状，如图2～图4所示。由图2～图4可知，随着参数α取值的变小，α-BBC越来越远离其骨架。故在实际应用中，可通过修改参数α的取值实现对α-BBC的形状调整，这也是传统球域Bézier曲线无法比拟的。

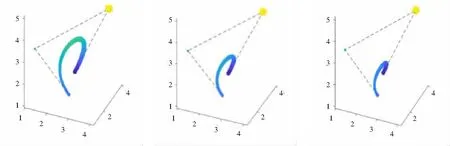
(a) α=1 (b) α=0.6 (c) α=0.4图2 参数α取不同值时的三次α-BBC

(a) α=1 (b) α=0.5 (c) α=0.2图3 参数α取不同值时的四次α-BBC

(a) α=1 (b) α=0.45 (c) α=0.01图4 参数α取不同值时的五次α-BBC

3 α-BBC的拼接

设有2条次数分别为m与n的α-BBC，其表达式分别为

(8)

式中gm,i(α1;t)(i=0,1,…,m)与hn,j(α2;t)(j=0,1,…,n)为参照式(2)与式(3)定义的α-Bernstein基函数，〈pi;ri〉(i=0,1,…,m)与〈qj;sj〉(j=0,1,…,n)为2条α-BBC的控制球。

由于控制球的半径各不相同时，球Bézier曲线的表面结构比较复杂，故一般只考虑2种情形下球域Bézier曲线的G1拼接[4]：1)围绕拼接点的控制球半径为零时球域Bézier曲线的G1拼接；2)所有控制球的半径均相同且不为零时球域Bézier曲线的G1拼接。

因此，这里也仅考虑上述2种情形下2条α-BBC的G1拼接。为方便讨论，不妨令式(8)表示的2条α-BBC的骨架分别为

于是，参照文献[4]可得如下结论。

定理2：对于式(8)表示的2条α-BBC，当控制球的半径满足rm-1=rm=s0=s1=0时，若2条α-BBC的骨架p(t)与q(t)之间达到G1拼接，即

(9)

其中λ>0，则2条α-BBC之间达到G1拼接。

注2：若某条α-BBC的首、尾均需进行拼接，则由定理2的条件可知，该条α-BBC的次数至少应为5次才能满足要求。

定理3：对于式(8)表示的2条α-BBC，当控制球的半径满足ri=sj=c(i=0,1,…,m;j=0,1,…,n;c为不等于零的常数)时，若2条α-BBC的骨架p(t)与q(t)之间达到G2拼接，即

(10)

其中λ>0，μ∈R，则2条α-BBC之间达到G1拼接。

在实际问题中，可通过取定合适的控制球使得定理2或定理3成立，从而实现2条α-BBC的G1拼接。例如，对于式(8)表示的2条α-BBC，当控制球的半径满足rm-1=rm=s0=s1=0，球心pm-1、pm=q0、q1共线时，不难可知式(9)成立，此时2条α-BBC之间达到G1拼接。若修改其中一条α-BBC所含的自由参数，则仅会对该条α-BBC的形状产生影响，此时可实现G1拼接α-BBC的局部调节，如图5所示；若将2条α-BBC所含的自由参数取为相同，则可通过修改这个相同的参数实现对G1拼接α-BBC的整体调节，如图6所示。

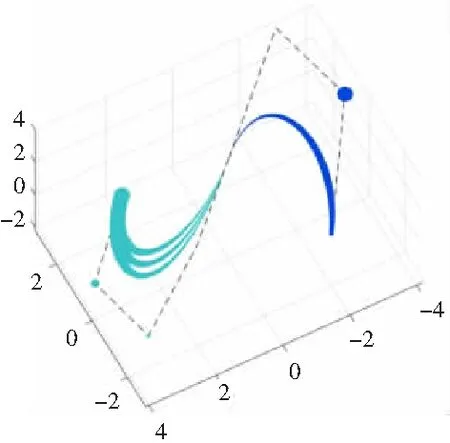
图5 自由参数对G1拼接三次与四次α-BBC的局部调节

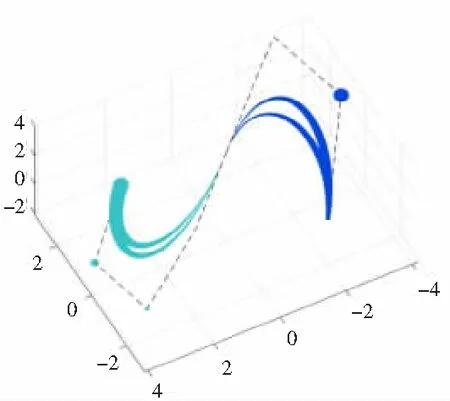
图6 自由参数对G1拼接三次与四次α-BBC的整体调节

图5中，三次α-BBC的参数取为α1=0.7且保持不变，四次α-BBC的参数分别取为α2=0.9与α2=0.5；在图6中，三次α-BBC与四次α-BBC的参数相同，且分别取为α1=α2=0.7与α1=α2=0.9。

下面再给出2个由α-BBC进行实体造型的实例。图7为利用三次α-BBC构造而成的灯笼，灯笼的顶部与底部为满足G1拼接的三次α-BBC；图8为利用三次α-BBC与四次α-BBC构造而成的蝴蝶。

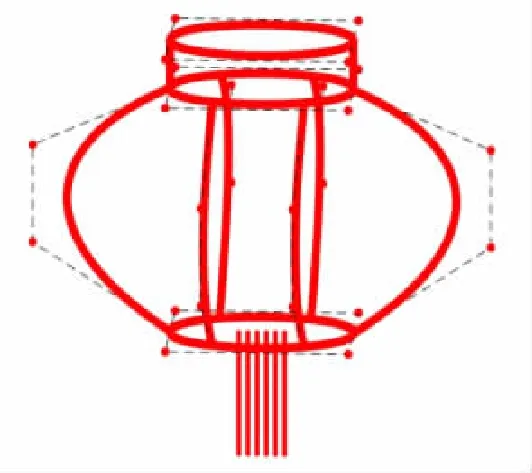
图7 灯笼造型

图8 蝴蝶造型

4 结束语

本文将α-Bézier曲线的控制顶点替换为控制球，构造了一种带形状参数的球域Bézier曲线。该球域Bézier曲线与传统球域Bézier曲线的性质类似，而且在控制球不变时可通过修改所含参数的取值实现对其形状的自由调整，从而进一步拓宽了球域Bézier曲线的应用，也为具有可变厚度的管状物体造型提供了一种有效手段。