农田水利流域无人机遥感影像拼接优化研究
涂 明,章李乐
(南昌市水利规划服务中心,330009,南昌)
0 引言
遥感技术已被广泛应用于农田水利中农田防洪抗旱、农业灌溉、农田水土流失、河道动态变化等监测与评价[1],但由于受卫星遥感重复周期、云雾遮挡等影响,卫星光学遥感往往难以满足农田防洪抗旱等对时效性、监测频率要求较高的关联流域监测应用。而无人机低空遥感能快速、频繁地获取农田水利流域现状高分辨率影像,可在一定程度上弥补卫星光学遥感流域监测在时效性等方面的不足,在农田水利关联流域监测应用优势十分突出。然而,相比陆域,农田水利流域位于低洼处,地形可能更为复杂,且流域范围内含有大面积水域,水域纹理不够丰富。当前基于特征点的无人机遥感影像匹配可能造成因同名点分布不均匀影响影像拼接质量。迄今为止,为解决诸如农田水利流域复杂地形下影像匹配问题,国内外针对多基元特征提取、仿射不变性匹配进行了深入研究。针对视点差异立体影像中同名点相似性测度邻域几何透视变形问题,现有匹配算法大多采用仿射变换模型来近似模拟同名区域透视变形,并通过提取仿射不变性的基元特征来进行相似性度量和匹配[2]。Mikolajczyk等[3]提出模拟仿射不变性的物方平面几何变形特征点检测算法;Matas等[4]提出了能抵抗光照、尺度、视点等变化的基于影像最大稳定极值区域(MSER, Maximally Stable Extremal Regions)的匹配方法和得到了较高的极几何估计精度;Mikolajczyk等人[5]通过试验对比了Hessian-Affine、Harris-Affine、MSER等常用算法的特征提取仿射不变性能,相比而言,MSER算法具有最佳的影像几何仿射不变性,因此,以基于MSER算法的面基元提取与匹配被广泛应用于解决摄影测量立体像对局部几何仿射不变性,常选用其MSER边界点进行精确匹配[6],或以拟合MSER区域椭圆范围建立相似性测度描述向量进行匹配;Song等[7]提出基于迭代模拟单应矩阵透视变换的倾斜航空影像匹配方法,Yang等[8]构造旋转不变描述子进行影像匹配;张永军等[9]提出了基于改进SIFT算法的低空影像匹配方法与大倾角影像匹配粗差剔除算法,能适应地形平坦情况下大旋偏角立体影像匹配;杨化超等[10]提出了一种基于SIFT算法适应地形起伏较大的低空遥感影像匹配和解决宽基线大旋偏角立体像对匹配的方法;吴军等[11]提出了仿射变换模拟几何变形的Affine-SIFT宽基线立体匹配方法;曹林[12]针对利用倾斜影像线特征进行匹配三维建模;陈敏等[13]提出结构自适应匹配方法解决宽基线城区立体像对因视角变化产生的局部变形问题;姚永祥等[14]提出结合加权力矩与绝对相位的影像匹配方法;肖雄武等[15]提出适用于倾斜影像视点几何仿射不变性的快速特征提取与匹配方法。
涉及复杂地形如农田水利流域及周边区域的低空遥感影像,因立体像对视点变化较大,利用简单的几何仿射变换而非透视投影变换模型来模拟影像特征局部几何变化以表述特征进行匹配容易失败[16],难以解决农田水利流域及周边地形起伏造成影像几何复杂变形给特征匹配带来的问题。针对上述分析,本文研究基于点-面多基元的农田水利流域无人机摄影测量匹配方法,从影像几何变形与点特征定位偏与偏差补偿出发,研究基于MSER、Harris-Laplace算法对农田水利流域复杂地形下低空影像匹配的方法,旨在实现适合包括水域、平地、山区等各种复杂地形的低空立体影像自动匹配,并设计出耦合点面特征多基元的影像匹配技术路线。
1 方法
针对农田水利流域复杂地形下低空影像特点,本文分别研究改进的MSER区域提取与重心定位方法;另一方面研究点-面多基元特征提取、定位与匹配方法,匹配基元特征池建立方法,结合三角网约束、核线与最小二乘法搜索同名点,实现点-面多基元的影像匹配及拼接优化,技术路线如图1所示。
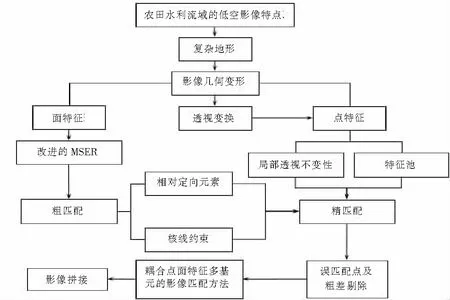
图1 技术路线
1.1 点-面多基元提取
本文耦合点-面特征多基元的影像匹配算法进行无人机遥感影像匹配,主要涉及点基元、面基元提取。MSER算子提取的面特征(区域)能抵抗影像局部几何变形,故适用于农田水利流域复杂地形下的影像匹配。然而,MSER算子在摄影测量精度方面有所不足,光照差异、噪声等易对灰度变化产生影响,造成局部相似区域提取的边界不重合。同时,针对农田水利流域低空立体像对在几何、灰度等变化较大,点特征可能出现叠置现象,点特征定位存在偏差,不能满足摄影测量点位高精度需要。因此,本文采用改进的MSER算法和点特征Harris-Laplace提取算法进行点、面基元提取。
1.1.1 优化的MSER面基元提取 MSER算法主要基于类似分水岭的思想来检测影像中具有高稳定不变性的图斑区域,该算法通过给定的阈值对灰度影像进行二值化分割,阈值从0~255依次取值递增进行分水岭分割,并生成一系列二值图;同时,反转原灰度影像,重复前述过程,则这2种操作分别被称为正向MSER和反向MSER,即MSER+和MSER-,并形成相应的稳定图斑区域。基于MSER算法的原理,其表达式为:
(1)
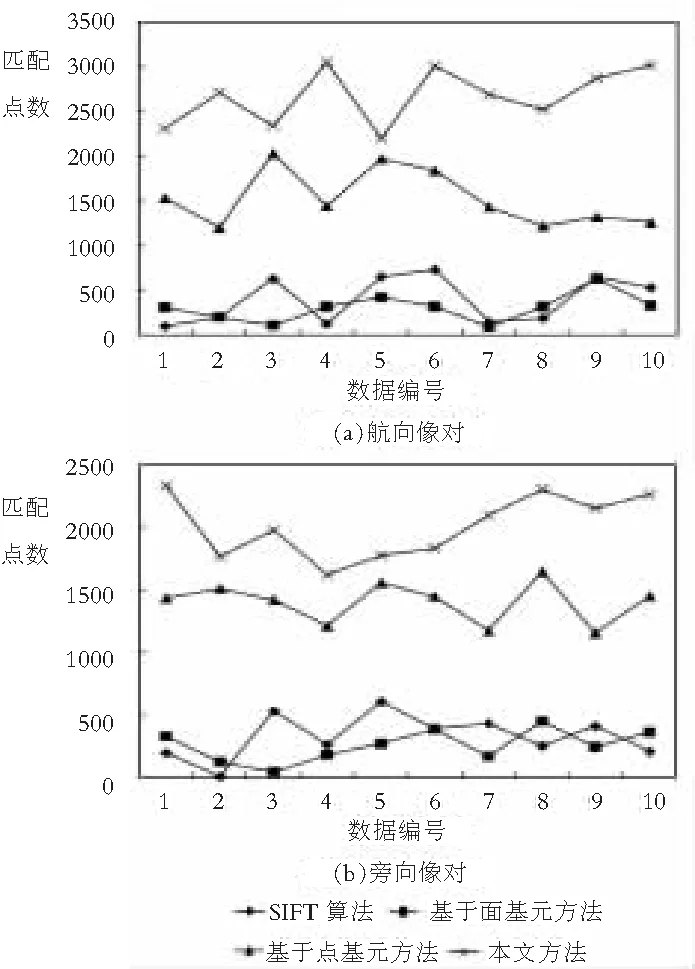
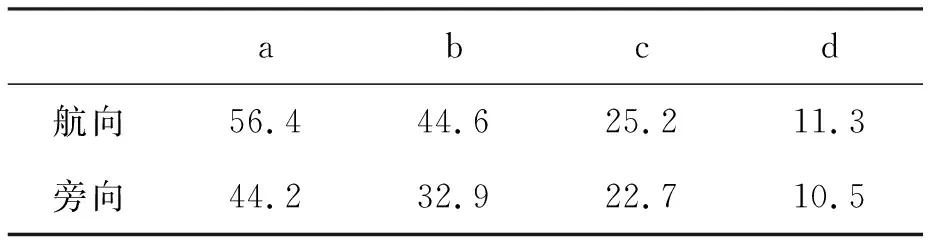
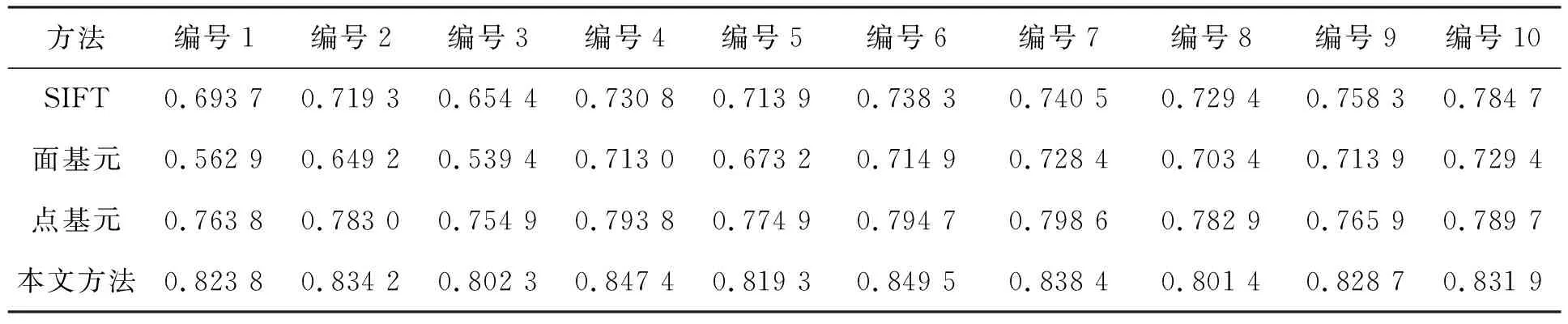
式中:Δ表示增量大小,R(i)表示阈值为i(0 图2中,R1和R2为立体像对中左、右影像提取的MSER同名面基元,易知左、右影像因成像时间、视点等差异造成提取的MSER面基元边界存在差异,面基元中心显然出现偏差,而不能满足依赖于点坐标进行高精度匹配需要。为提高立体像对间区域特征可重复性,引入边缘检测算法,研究增强图像边缘对相同区域提取的MSER边界吻合程度的影响;同时,研究以MSER算法进行宽基线大倾角影像粗匹配,针对立体像对局部相同区域因灰度强度差异,使得检测出的同区域的MSER边界不完全吻合,引入迭代选权最小二乘法构建误差方程计算MSER面特征的重心,比较分析重心优化后较之MSER中重心定位法在极几何与相对定向精度方面的提高。该研究可为影像精匹配提供更为精确的核线关系。 图2 像对相似区域MSER边界对比 本文以三次多项式为目标函数拟合MSER边界,该函数为: F=h1x2+2h2xy+h3y2+2h4x+2h5y+1 (2) 设M估计的函数F取为F(vi),M估计的准则为 (3) 通常残差矩阵V为未知参数,对公式(3)的未知参数进行一阶求导,并令等式为零以求出极值点。 (4) 式中:h1~5是目标函数的系数,(x,y)为像素点的坐标,构建误差方程: (5) (6) 式(6)中,P表示权矩阵,本文采用选权迭代法确定最优权值[17],其函数表达式为 (7) (8) 式中:v、σ分别为残差和中误差,则式(6)可改化为 (9) 式中:diag表示对角矩阵,λ表示迭代最小二乘收敛参数。通过公式(8)减少残差,并采用最小二乘迭代选权法解算各待求参数值,其迭代运算过程为 (10) 式中:X=[h1,h2,h3,h4,h5],X0为X的初值。然后,MSER面基元的中心为优化后的椭圆中心。 1.1.2 基于Harris-Laplace的点基元提取 参考前人研究[17],利用Harris-Laplace算法,考虑Harris角点响应函数与面特征获得透视变换几何变形特征,构建误差方程,通过迭代精化,获得最佳的亚像素Harris-Laplace角点,实现农田水利流域复杂地区无人机摄影测量点基元提取。 1.1.3 特征描述与匹配 由于农田水利流域无人机飞行姿态受风力影响,本文采用具有尺度、旋转、光照与平移不变性的SIFT(Scale Invariant Feature Transform)算法进行低空遥感影像特征描述[18],采用高斯差分函数DoG(Difference of Gaussian)在影像金字塔空间内检测极值点,该表达式为 D(x,y,σ)=(G(x,y,kσ)-G(x,y,σ))*I(x,y)=L(x,y,kσ)-L(x,y,σ) (11) 其中: L(x,y,σ)=G(x,y,σ)*I(x,y) (12) (13) 式中:σ为尺度参数,G(x,y,σ)表示尺度变换高斯函数,I(x,y)表示二维影像,(x,y)为像素点坐标。SIFT算法计算特征点周围像素梯度方向(0°~360°),并在每隔45°的空间内统计以确定特征点主方向,其像素梯度与方向计算公式为 (14) 式中:m(x,y)、θ(x,y)分别表示在影像位置(x,y)的梯度和方向,特征描述采用4×4×8=128维的向量矩阵来表征特征点,本文采用欧式距离作为相似性度量与特征匹配。同时,以单应矩阵表征立体像对间局部几何变换关系,并结合随机采样一致性RANSAC(Random Sample Consensus)算法和概率统计来迭代剔除误匹配点和实现特征点精匹配。 1.1.4 三角网与核线约束 根据构建的TIN三维表面模型,研究在TIN三角网映射至立体像对中的三角格网内创建点特征基元局部透视不变性囊括灰度、纹理、梯度等多特征信息描述的特征池作为匹配测度,自适应改变相似性测度窗口形状,结合三角网约束、核线与最小二乘法实现农田水利流域复杂地形下低空立体像对分布均匀的同名点匹配。 同时,采用核几何约束将面基元中心匹配由二维空间搜索缩小到一维空间以提高匹配效率,并采用双向匹配减小误匹配概率。核几何约束左影像特征点目标区和右影像匹配点搜索区分别位于重叠影像的同名核线上,以面基元待匹配点为中心,在待匹配影像同名核线上逐像素点为中心和周围建立搜索窗口,分别计算目标窗口和待匹配影像核线上搜索窗口的欧式距离,把欧式距离最小的面元中心点视为候选匹配点。 模拟TIN格网透视变化,结合局部近似平面区域点特征透视变换规律,研究利用单应矩阵构建具有尺度不变性、抵抗噪声影响和影像几何变形的点位偏差补偿机制,在三角网约束下提取分布均匀的高精度亚像素Harris-Laplace角点。 本文采用摄影测量相对定向方法解算核几何参数,以目标影像空间坐标系为基准,按共面条件列出待匹配影像上像素点坐标(u2,v2,w2)变换到目标影像像素点坐标(u1,v1,w1)的关系式为 (15) 式(15)展开得: (16) L1y1x2+L2y1y2-L3y1f+L4x2f+L5y2f-L6ff+L7x1x2+L8x1y2-L9x1f=0 (17) 公式(17)两边同除L5后可减少一个未知参数,其表达式为 (18) 本文采用点-面基元耦合的低空遥感影像匹配方法,在通过高斯滤波建立的影像金字塔结构顶层进行初匹配,得到立体像对间初始定向与核几何关系,在目标影像上提取Harris-Laplace亚像素角点,通过核几何约束在右影像搜索同名点,并利用最小二乘得到匹配点。主要步骤如下。 1)构建高斯影像金字塔结构,利用MSER面基元在金字塔顶层进行影像粗匹配,并获得影像间初始定向关系。 2)在目标影像上提取Harris-Laplace亚像素点基元。 3)基于1)中的初始定向关系,通过核几何约束和最小二乘匹配在待匹配影像一维空间目标影像Harris-Laplace亚像素点基元的匹配点。 4)利用RANSAC算法剔除误匹配点和粗差获得立体像对同名点。 采用基于泊松融合的影像拼接技术[19],利用本文匹配方法得到的匹配点和相对定向关系,优化影像间转换矩阵的参数,实现无人机遥感影像拼接优化。 为对比分析立体影像像对拼接效果,采用立体像对间重叠区相关系数来评价拼接误差[20],其计算公式为: (19) 为验证本文基于点-面多基元的影像匹配及在影像拼接优化方面的实用性及可靠性,采用多组农田水利流域无人机低空遥感影像进行实验。分别选取具有典型农田水利流域地形的低空航向和旁向影像像对各10对,并采用2个测区数据进行拼接效果验证。 同时,为了便于比较分析匹配点数量、质量及运算效率,采用SIFT算法、基于面基元匹配(MSER)、基于点基元匹配(Harris-Laplace)、本文方法4种方法进行匹配对比试验,同名点数量统计结果见图3。可知,本法方法在农田水利流域航向和旁向像对匹配点数量明显超过另外3种方法。 图3 4种方法匹配结果统计 4种方法在相同软硬件环境下进行匹配的平均时间见表1。可见,本文方法加入了多基元提取与匹配虽然耗费数据处理时间,但缩小了像对间匹配点搜索空间,使得立体像对匹配效率并未降低,反而相比其它3种方法,本文方法效率提高了至少2倍。 表1 4种方法各自平均匹配时间/s 选择本文方法匹配得到的具有代表性的2组立体像对可视化结果见图4,可见本文方法得到的匹配点数量可观且分布均匀,图4(a)和(b)的匹配点数分别为2 032和3 869。由实验结果可知,本文方法在农田水利流域复杂地形下低空遥感影像匹配中具有较强的实用性和可靠性。同时,也选取了2个序列的农田水利流域复杂地形的低空影像进行匹配、相对定向、拼接等实验验证本文方法所得到效果见图5。本文利用Huber法能有效地减少立体像对间匹配点残差,也可降低农田水利流域无人机遥感影像拼接过程中粗差对立体像对间几何变换模型求解的影响和接边误差。 图4 2组立体像对匹配结果 图5 流域区域低空影像匹配及拼接 此外,采用SIFT算法、基于面基元匹配、基于点基元匹配、本文方法匹配得到的转换参数进行10对立体像对拼接重叠区相关系数值统计见表2,可知,SIFT算法优于基于面基元的方法,而基于Harris-Laplace点基元的方法优于SIFT算法和面基元,而本文算法得到相关系数值最高,都大于0.8,表明结合点-面多基元匹配后进行拼接优化可显著提高农田水利流域无人机遥感影像拼接质量,同时也验证了本文方法匹配点数量与质量可明显优化影像间转换矩阵的参数。 表2 拼接重叠区相关系数对比 为使农田水利流域无人机遥感影像匹配方法能抵抗立体像对平移、旋转、光照、尺度、仿射变化,提出了基于点-面多基元的匹配方法,通过MSER算法提取面基元进行初匹配,利用亚像素Harris-Laplace算法、核几何和最小二乘实现立体像对特征点精匹配。利用具有光照、平移、旋转、尺度、仿射变化较大以及重复纹理的农田水利流域无人机低空立体影像进行匹配试验,表明了本文方法比单一的匹配方法(如SIFT算法、基于面基元匹配、基于点基元匹配)更为可靠、稳健,能得到分布均匀、数量足够的同名点,本文方法对于农田水利流域低空摄影测量等不规则测量方式影像处理具有重要的实用价值。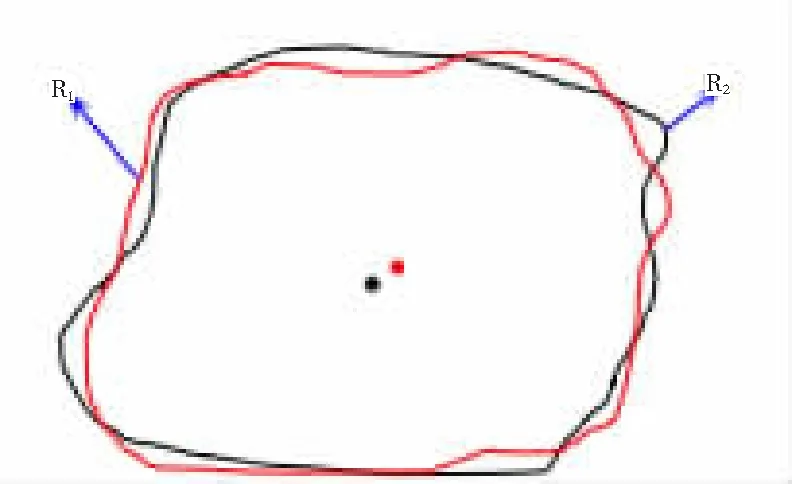
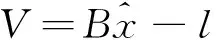
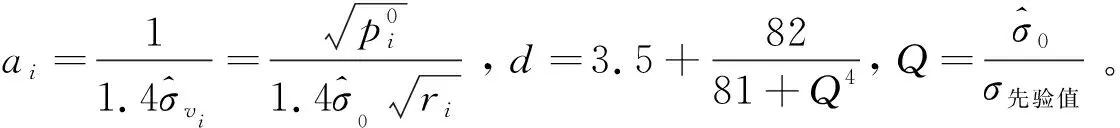
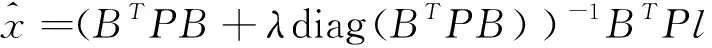
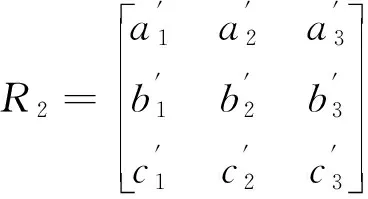
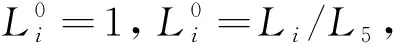
1.2 影像匹配与拼接
1.3 影像拼接误差指标
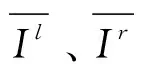
2 实验结果与分析


3 结论

