高阶中心对称张量谱理论及应用*
许 娜, 王春燕
(①曲阜师范大学公共外语教学部;② 曲阜师范大学管理学院,276826,山东省日照市)
0 引 言
中心对称矩阵和斜中心对称矩阵在信息论、线性系统理论和数值分析中起着重要作用[1,2,6-8,14,15,20,22,24,26]. 关于中心对称矩阵的理论及应用研究可追溯到19 世纪60 年代[19]. 20 世纪 80 年代,随着大数据时代的来临,大规模数椐分析及应用发展迅速,高阶张量研究引起了越来越多科研工作者的研究兴趣,具有特殊结构的高阶张量已被广泛应用于非线性动力系统,多项式优化及工程和科学计算等实际问题. 赵和杨[27]首次给出了高阶中心对称张量的定义,并讨论了非负中心对称张量的特征值性质[27]. 本文继续对高阶中心对称张量的结构性质与谱理论展开研究,并将其应用到柯西张量的特征值计算等问题.
本文所探讨的张量可以称作超矩阵,即矩阵的元素有两个下标,而超矩阵的下标有m个,其中m称为这个超矩阵的阶. 显然,零阶超矩阵即为标量,一阶超矩阵即为向量,二阶超矩阵即为矩阵. 首先,简单回顾高阶张量的一般定义及特征值等基本概念. 一个m阶n维张量可以表示成A=(ai1i2…im),ai1i2…im,1≤ij≤n,1≤j≤m称作张量A的元素. 其中aii…i,1≤i≤n为张量A的对角元,其余元素为A的非对角元. 如果
ai1i2…im∈,ij∈[n],j∈[m],
则张量A为一个实张量.
在本文中,只考虑实张量的情况. 如果元素ai1i2…im在其指标的任意排列下是不变的,则张量A称为对称张量.
定义1 假设一个m阶n维实张量A=(ai1i2…im)满足ai1i2…im=an-i1+1,n-i2+1,…,n-im+1,ij∈[n],j∈[m],则称张量A为中心对称张量. 如果ai1i2…im=-an-i1+1,n-i2+1,…,n-im+1,ij∈[n],j∈[m],则称张量A为斜中心对称的.


高阶中心对称张量和斜中心对称张量属于结构张量,结构张量的研究属于多线性代数的范畴. 随着人们对多线性代数研究的兴趣日益浓厚,越来越多的结构矩阵被推广到高阶结构张量,并发现了许多新颖而有意义的结论,为多线性代数与运筹学,计算机科学等交叉学科的发展提供了理论依据.
本文主要结构分为5节. 第1节回顾了高阶张量和多项式优化的一些基本定义及部分重要结论. 第2节证明了中心对称张量和斜中心对称张量的各种性质,例如中心对称张量积的不变性、左逆张量和右逆张量的遗传性等. 此外,还证明了高阶张量为中心对称或斜中心对称结构的充要条件. 第3节讨论了中心对称张量和斜中心对称张量的特征值性质. 特别地,对于二维与三维张量,证明了其H特征值总是具有对称H特征向量或斜对称H特征向量,并进一步证明了斜中心对称张量的所有非零H特征值总是成对出现. 第4节对具有中心对称结构的柯西张量展开研究,建立了中心对称柯西张量可检验的充要条件. 还证明了中心对称柯西张量的最大(最小)H特征值等价于一类低维的柯西张量的特征值,进而降低计算难度. 第5节总结本文主要内容并列举了下一步的几个研究方向.
1 预备知识
在本节中,回顾张量特征值及张量与多项式的关系等基本定义,包括张量积、H特征值和H特征向量的概念. 首先列举常用的一些符号,假设n为一个整数,定义集合[n]=1,2,…,n. 全体m阶n1×n2×…×nm维实(复)张量构成的全体记作n1×n2×…×nm(n1×n2×…×nm).
对于x∈n,定义xm为一个m阶n维对称秩1张量,它的元素满足
(xm)i1i2…im=xi1xi2…xim,ij∈[n],j∈[m].
特别地,任意一个m阶n维张量A在n空间中对应一个m次齐次多项式如果张量A为对称张量,则相应的齐次多项式是唯一的. 当m=2时,该齐次多项式退化为二次型. 同样的,n空间上的任意m次齐次多项式函数fA(x)也对应唯一的对称张量.
接下来回顾张量乘积的概念.
定义2[3]设A∈n1×n2×…×n2,B∈n2×n3×…×nk+1并且m≥2,k≥1. 则AB乘积为元素满足下列条件的(m-1)(k-1)+1阶的张量C
其中i∈[n1],α1,α2,…,αm-1∈[n3]×…×[nk+1].
本文主要研究n1=n2=…=nk+1=n时的情况. 针对此特殊情形,邵等在文献[17]给出了张量乘积的定义. 接下来,引入张量特征值的定义.
定义3 假设T=(ti1i2…im)为一个m阶n维实张量. 如果存在一组(λ,x)∈×n{0}满足
Txm-1=λx[m-1],
(1)

2中心对称张量和斜中心对称张量
本节主要研究高阶中心对称张量与斜中心对称张量部分性质及特征值理论. 首先证明中心对称张量的乘积不变性,即中心对称张量与中心对称张量的乘积仍然是中心对称张量. 其次,提出了中心对称张量或斜中心对称张量的几个充分必要条件. 最后证明了中心对称张量和斜中心对称张量的左逆和右逆的性质. 当阶数等于2时,即中心对称矩阵的性质和应用,请参阅文献[7,8,14,15,20,22,24].
引理1 假设B是n×n阶中心对称矩阵,A是m阶n维中心对称张量,那么BA是m阶n维中心对称张量.

据此,根据定义1,得到BA是一个m阶n维的中心对称张量.
同理,可证明如下结论.
引理2 假设A和B如引理1所定义. 则AB是中心对称张量.
证明由定义2以及A和B是中心对称的,可得对任意i1,i2,…,im∈[n],有
因此,AB是一个中心对称张量.
引理1与引理2给出了中心对称张量与矩阵乘积的不变性,定理1证明了中心对称张量乘积的不变性.
定理1 设A与B分别为m阶n维和k阶n维中心对称张量,则AB是一个(m-1)(k-1)+1阶n维中心对称张量.
证明由定义2可知,对任意的
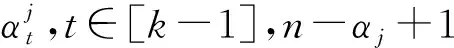
根据定理1,可得如下推论.
推论1 假设A与B如定理1所定义. 那么下述结论成立:
(ⅰ) 如果张量A是斜中心对称的,张量B是中心对称的,那么AB是斜中心对称的;
(ⅱ) 如果张量A是中心对称的,张量B是斜中心对称的,那么当m是奇数时,AB是中心对称的;当m是偶数时,AB是斜中心对称的;
(ⅲ) 如果张量A和张量B都是斜中心对称的,那么当m是偶数时,AB是中心对称的;当m是奇数时,AB斜中心对称的.
推论2 对任意有限个n维张量A1,A2,…,As,如果它们都是中心对称张量,则乘积A1A2…As也是中心对称张量.
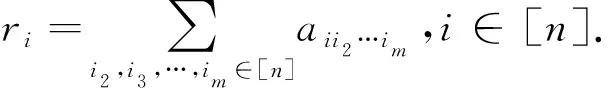
定理2 设A=(ai1i2…im)是m阶n维张量. 如果A是中心对称张量,则ri=rn-i+1,i∈[n];如果A是斜中心对称张量,则ri=-rn-i+1,i∈[n].
推论3 设张量A如定理2所定义,假设n为奇数. 如果A是斜中心对称的,那么它至少存在一个非零元素且至少存在一个i∈[n]满足ri=0.

下面研究中心对称张量与斜中心对称张量的充分必要条件. 首先,假设J是一个由jij=δin-j+1,1≤i,j≤n,组成的n×n的实矩阵,其中δin-j+1表示克罗内克符号,即有

定理3 设A是m阶n维张量. 那么A是中心对称的当且仅当JAJ=A;A是斜中心对称的当且仅当JAJ=-A.
证明对任意的ij∈[n],j∈[m],由定义2可得
即,当且仅当JAJ=A时,A是中心对称的. 同理可得第2个结论也成立.
很明显JJ=I,其中I是n×n单位矩阵. 由于定义2中的张量积满足结合律(见文献 [17] 的定理1.1),故有如下结论.
定理4 设A是m阶n维张量. 则当且仅当AJ=JA时,A是中心对称张量;当且仅当AJ=-JA时,A是斜中心对称张量.
设x=(x1,x2,…,xn)∈n. 那么Jx是通过将x的元素顺序颠倒来得到一个向量. 如果Jx=x,我们说x是一个对称向量,如果Jx=-x,则它是中心对称的. 对任意给定的m阶n维张量A=(ai1i2…im),它对应的齐次多项式可以表示为
定理5 设A为m阶n维中心对称张量. 对任意x∈n,有f(Jx)=f(x);如果A是斜对称张量,那么f(Jx)=-f(x).
证明设y=Jx=(xn,xn-1,…,x2,x1),即yi=xn-i+1,i∈[n]. 如果A是中心对称的,那么可知
(2)
当A是斜中心对称的,则有
(3)
根据式(2)和式(3),结论成立.
假设A=(ai1i2…im)和B=(bi1i2…im)是两个m阶n维张量,A和B的 Hadamard 积定义为
A∘B=(ai1i2…imbi1i2…im).
(4)
上式所得张量仍是m阶n维的.
根据定义1和式(4),下面定理显然成立.
定理6 已知m阶n维张量A和B,则如下结论成立:
(ⅰ) 如果A和B都是中心对称的,那么A∘B是中心对称的;
(ⅱ) 如果A和B都是斜中心对称的,那么A∘B是中心对称的;
(ⅲ) 如果A是中心对称的,B是斜中心对称的,那么A∘B是斜中心对称的.
众所周知,任何矩阵都可以分解为对称矩阵和斜对称矩阵的和. 类似地,有以下结论.
定理7 对于任意给定的m阶n维张量A,它可以表示为一个中心对称张量和一个斜中心对称张量的和.

中心对称矩阵的另一个重要性质是它的逆矩阵也是中心对称的[22]. 因此,我们想知道一个中心对称张量的逆是否为中心对称的. 然而,张量的逆至今没有明确定义. 但是,张量左逆和右逆的定义在文献[3]中给出. 在下面的分析中,将研究左逆张量和右逆张量的中心对称性质.
在文献[3]中给出了张量的左逆和右逆的定义.
定义4[3]设A是一个m阶n维张量,B是一个k阶n维张量. 如果AB=I,那么A是B的一个m阶左逆,B是A的一个k阶右逆.
定理8 假设A=(ai1i2…im)是一个m阶n维对角中心对称张量. 则有下述结论成立:
(ⅰ)A有中心对称左逆,当且仅当A有非零对角元素;
(ⅱ) 当m是偶数时,A有中心对称右逆,当且仅当A有非零对角元素;
(ⅲ) 当m是奇数时,A有中心对称右逆,当且仅当A所有对角元素都是正的.
证明(ⅰ) 根据定义4,A有中心对称左逆,当且仅当存在k阶n维实中心对称张量B=(bi1i2…ik)满足
BA=I.
(5)

(ⅱ)假设B=(bi1i2…ik)是k阶n维中心对称张量满足
考虑AB的对角线元素,可以得到
(6)
这表明A有非零的对角元素.


定理9 设A是m阶n维中心对称张量. 如果A有2阶n维实左逆,则该逆是唯一的且为中心对称矩阵.

由A的中心对称性可知B-1是中心对称矩阵矩阵. 因为中心对称矩阵的逆矩阵是中心对称的(见文献[22],命题6),可知B是中心对称张量.
另一方面,假设A有另一个2阶左逆C. 由此可得A=B-1I=C-1I,其中C-1是C的逆. 进而,(B-1-C-1)I=0.根据文献[3]中引理 2.1可得B-1=C-1,所以B=C,结论成立.
根据定理9的证明,同理可得如下定理.
定理10 假设A是m阶n维的中心对称张量,其中m是偶数. 如果A有2阶n维右逆,则该逆唯一且为中心对称矩阵.
3 中心对称张量和斜中心对称张量的谱性质
本节针对高阶中心对称张量和斜中心对称张量的H特征值和H特征向量的展开研究. 在文献[22]中,作者证明了2×2阶或3×3阶中心对称矩阵的所有特征向量都是对称或斜对称的. 但是,这一性质并不能推广到4×4阶矩阵的情形. 下面2个定理证明m阶2维和m阶3维中心对称张量总是具有对称H特征向量或斜对称的H特征向量.
定理11 设A=(ai1i2…im)为m阶2维的中心对称张量,则
分别为张量A的对称H特征值与斜对称H特征值.
证明设e=(1,1)T,u=(1,-1)T. 由定义3及A中心对称性可知
结论得证.

证明令x=(1,0,-1)T,由定义3可得
(7)
因为A是中心对称张量,且m为偶数,故有
(Axm-1)3=-(Axm-1)1.
(8)
另一方面,
故
(Axm-1)2=0.
(9)
由式(7)~(9)可得λ为张量A的斜对称H特征向量x对应的H特征值.
下面针对一般H特征值情形展开研究. 一方面,当H特征向量元素的顺序颠倒时,它仍然是相对应的H特征向量. 另一方面,对于斜中心对称张量,如果λ∈是斜中心对称张量的H特征值,则-λ也是张量的H特征值,这意味着给定斜中心对称张量的H特征值成对出现.
定理13 设A为m阶n维中心对称张量. 如果x∈n为张量A对应于H特征值λ的H特征向量,则Jx为张量A与λ相对应的H特征向量.
证明由定义及(1),可以得到Axm-1=λx[m-1].令x=(x1,x2,…,xn),则Jx=(xn,xn-1,…,x1). 对任意的i∈[n],可以得到
(10)
由上式可以得到Jx为张量A的对应于特征值λ的H特征向量.
同理可得到如下结论,证明过程与上述定理类似,故略去证明细节.
定理14 设A为m阶n维斜对称张量. 如果λ∈为张量A的对应于H特征向量x的H特征值,则-λ为张量A对应于H特征向量Jx的H特征值.
定理15设A=(ai1i2…im)为m阶n维中心对称张量. 对于张量A的所有H特征向量及对应的H特征值λ,其中dimker(λI-A)=1,则H特征向量是对称或斜对称特征向量.
证明假设x∈n为张量A的H特征值λ对应的H特征向量. 由定义3可得
Axm-1=λx[m-1].
(11)
因为A为中心对称的,由定理3和式(11)可得JAJxm-1=λx[m-1].由上式可得
AJxm-1=λJx[m-1]=λ(Jx)[m-1].
(12)
此外,由定义1可得
对任意i∈[n]都成立,故
AJxm-1=A(Jx)m-1.
(13)
由式(12),式(13)可得A(Jx)m-1=λ(Jx)[m-1],这说明Jx是与特征值λ相对应的H特征向量. 根据dimker(λI-A)=1,可得Jx=ax,其中a为非零实常数,a也是矩阵J的特征值. 则a=±1. 因此,Jx=±x,这意味着x要么是对称的,要么是斜对称的.
4 中心对称柯西张量及应用
本节拟将中心对称张量应用于高阶柯西张量,并详述此类张量的特征值性质与计算. 首先证明了柯西张量为中心对称张量的可检验的充分必要条件. 其次证明了不存在任何奇数维斜中心对称柯西张量,当中心对称柯西张量为偶数阶时,对应于非零H特征值的所有H特征向量都是对称的;当阶数是奇数时,H特征向量的绝对向量是对称的. 更多关于非负对称张量的应用,请参阅文献[27].
下面给出柯西张量的定义.
定义5[4]设c=(c1,c2,…,cn)∈n. 假设一个实张量C=(ci1i2…im)的元素满足
(14)
则C被称作m阶n维柯西张量,向量c∈n称为张量C的生成向量.
4.1 中心对称柯西张量的充分必要条件
定理16 设C为m阶n维柯西张量. 令c∈n为张量C的生成向量. 则张量C为中心对称张量当且仅当c是对称的,即Jc=c.


由定理16和定理3,可得下面结论.
推论4 假设C如式(14)定义的柯西张量. 则C为中心对称张量当且仅当CJ=C,JC=C,其中J的定义见第3节.
下边定理证明了偶数维柯西张量是斜中心对称张量当且仅当它的生成向量是斜中心对称的. 因为证明过程与定理16类似,此处省略.
定理17 设C为m阶n维柯西张量且n为偶数. 则C为斜中心对称张量当且仅当c为斜对称向量,即Jc=-c,其中c∈n为张量C的生成向量.

定理18 设C为m阶n维柯西张量. 令c=(c1,c2,…,cn)为C的生成向量. 假设C为中心对称张量,则C的任意非零H特征值对应的H特征向量x∈n满足当m为偶数时,x是对称的;当m为奇数时,|x|为对称的.
证明根据已知条件柯西张量C为中心对称的,由定理16可得,生成向量c为对称的. 设x为C的H特征向量,对应的非零H特征值为λ. 由定义3,对于任意i∈[n],可得
当m为偶数时,xi=xn-i+1,i∈[n],即x为对称向量. 当m为奇数时,|xi|=|xn-i+1|,i∈[n],即|x|为对称向量.
4.2 中心对称柯西张量的最大(最小)H特征值
下面的引理将在后面的分析中起重要作用.

假设C为m阶n维中心对称柯西张量且m为偶数. 如果C所有的H特征值中最大(最小)值不等于零,由引理3和定理18可得
(15)
其中S⊆n为包含所有对称向量的子集.
定理19 设C为m阶n维中心对称柯西张量,令m为偶数且n=2k,其中k∈为正整数. 假设c=(c1,c2,…,cn)为C的生成向量. 如果C的最大(最小)H特征值不等于0,则其中是由k生成的m阶k维柯西张量.
证明首先,为了保持表示符号的简便性,定义如下指标集
I0={(i1,i2,…,im)∈[n]m|i1,i2,…,im≤k},Ir={(i1,i2,…,im)∈[n]m},r∈[m],
其中r表示(i1,i2,…,im)中有r个指标在区间[k+1,n]中取值. 因为C为偶数阶中心对称张量,由定理18可得,对于所有的H特征向量是对称的. 所以,对于任意的x∈S,‖x‖m=1,可得
(16)

定理20 设C是m阶n维中心对称柯西张量且m,n是偶数. 假设c=(c1,c2,…,cn)∈n,c>0是C的生成向量. 则其中为柯西张量的生成向量.
5 结 论
本文主要研究高阶中心对称张量和斜中心对称张量的各种性质. 例如,张量积的不变性,张量左逆和右逆的遗传性等. 其次,研究了H特征值的谱性质以及对中心对称张量的H特征向量的估计. 最后,将中心对称结构应用于高阶柯西张量,证明了高阶中心对称柯西张量的最大(最小)H特征值可等价转化为计算一个低维柯西张量一的H特征值.
然而,本文是对中心对称张量的初步研究,尚存许多待研究的问题.
问题1中心对称张量的正定性是怎样的? 能否给出一些类似于文献[1]中的矩阵情形下的充分条件?
问题2斜中心对称柯西张量的H特征向量的性质是什么?
问题3近几年,如引言所述,已经对各种结构的张量进行了研究[4,5,9-12,18,21,25],那么当中心对称结构应用到那些结构的张量时能得到什么重要结论?

