两种概率密度导数估计方法的比较研究*
王文武, 孔德茹
(曲阜师范大学统计与数据科学学院,273165,山东省曲阜市)
0 引 言
在探索样本总体信息时,概率分布函数及密度函数为统计研究的基本问题. 相应地,其估计理论已经得到较好的完善,但密度函数的导数却鲜少被关注. 虽然密度导数没有受到足够的重视,但是其作用不容小觑. 例如,一阶导函数为密度函数的斜率,反映了密度函数的波动幅度;二阶导函数为密度函数的曲率,反映了密度函数的弯曲程度以及光滑程度. 密度函数的导数不仅直观反映了概率密度的图像走势,而且被广泛应用于经济学与统计学等领域:在经济学中,常需要GDP(国民生产总值)进行建模并做出导数估计,利益的最值问题也需要导数或者偏导数的计算[1];在统计学中,概率密度函数的导数也发挥了重要作用,例如,导数作为重要的一环,出现在最速下降及牛顿等算法中.
因此,密度函数导数需要得到关注并且估计方法也应被深入研究. 从密度导数本身出发,Härdle等提出了平均导数估计并给出了实例应用[2];次年,又提出了一种广义交叉验证,通过利用差商的核平滑来估计一阶导数[3]. 2009年,Hansen在《Lecture Notes on Nonparametrics》书中总结了密度函数导数的简单估计方法——根据导数定义对密度函数的导数进行核估计[4]. 2013年,Chacón等提出了多变量数据下的核密度导数估计带宽选择器,优化了核方法在导数估计中的应用[5]. 近年来,回归函数的导数估计受到了重视,这为密度函数导数估计提供了新的思路.Charnigo等在2011年提出通过GCp标准选择合适的调整参数从而提高导数估计的效果,并且该方法可用于任何非参数回归方法[6]. 2013年,Brabanter等阐述了经验一阶导数在局部多项式回归框架中的使用,并推导了偏差和方差[7]. 2016年,Wang等将局部加权最小二乘方法以及差分方法应用到导数估计中,得到了更小的均方误差[8]. 2019年,Cattaneo等采用局部多项式回归估计各阶导数,给出了较为全面的软件包,并应用到断点回归的临界点检验中[9,10].
在估计概率密度导数时,尽管核方法和局部多项式回归方法经常被使用,但在应用中并不清楚哪种方法更有优势. 故本文从理论和模拟两个角度进行比较研究. 首先,对这两种非参数估计方法的理论知识进行了梳理总结并做出了合理的比较. 其次,选择均匀分布、正态分布、卡方分布,在不同样本量下对概率密度导数进行数值模拟并根据经验积分均方误差比较估计效果. 为了更充分地对比估计性质,每种方法均通过两个软件包实现. 通过观察两种方法在4个R包下均方误差值的变化以及估计结果图,最终证实局部多项式回归方法相较于核方法具有更加优良的性质.
1 两种估计方法
在总体信息模糊的情况下,常采用非参数方法来达到目的. 常见的密度函数估计方法有直方图法、核方法、局部多项式回归法、样条估计法以及最近邻估计法等,其中核方法和局部多项式回归法最为常用[11]. 本部分将简单介绍核方法和局部多项式回归方法的一般理论.
1.1 核方法
首先采用核方法估计概率密度函数,即核密度估计. 核密度估计通过核函数来估计未知的概率密度,其基本思想是按照其余观测值距估计点的远近对该估计点赋予不同的权重:距估计点较近的观测值包含该估计点较多的信息,所以赋予更大的权重;距估计点较远的观测值包含信息较少,故赋予较小的权重甚至0权重[10].
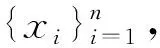
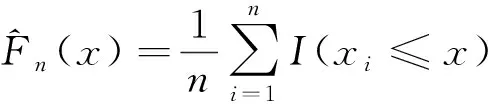
其中k(·)为核函数.通过核密度估计的最终形式可以看出核密度估计结果实际上是对协变量x附近的观测值进行加权平均,核函数为权重函数. 另外,核函数需要满足非负性、对称性、正则性等条件. 在有关核的应用中,均匀核函数、Bieweight核函数以及Gaussian核函数较为常见.
在核密度估计的基础上由导数定义,对估计得到的密度函数求r阶导[4],即

1.2 局部多项式回归方法
局部多项式回归方法作为非参数统计的一种重要估计方法,应用范围极其广泛. 其核心思想是在局部区域用某一多项式近似目标函数,从而得到该函数及其各阶导数的估计[12]. 估计过程中用到的多项式通常是采用泰勒展开得到的. 因此,当估计同一函数时,采用不同阶数的多项式将得到不同的估计效果[13].
在介绍局部多项式回归方法估计概率密度导数之前,作出两个一般假定[9].
假定1假定x1,…,xn是来自分布函数为F(x)的一组随机观测值,概率密度函数为f(x),其中,协变量x的定义域为[xlower,xupper](xupper≠xlower),分布函数F(x)至少p+1阶可导并且F(r+1)(x)=f(r)(x),r≤p.
假定2为了优化估计效果的表达式,本文要求核函数k(·)除满足一般性质外,还需要满足该条件:无论核函数为哪种形式,均只在[-1,1]上有意义,其余位置点为0.
注对于假定1的条件,几乎所有数据都可以满足.由于距离x越近的观测点包含的信息越多,给出的权重也应越大[14],故假定2把核函数的取值范围限制在了[-1,1]上,即在[x-h,x+h]上核函数非零.对于高斯核函数,虽不能满足该条件,但在[-1,1]之外的区域,核函数取值接近于0.因此可认为高斯核函数满足假定2中的限制.此外,当带宽接近于0时,假定2将核函数限制在估计点附近,从而可优化边界估计效果.
目标函数F(x)为x的分布函数,yi为F(x)的样本值,则有局部最小二乘估计

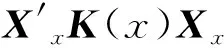
1.3 两种方法的估计效果
在衡量估计效果时,常采用积分均方误差MISE(Mean Integrated Squared Error),
从上式可以看出均方误差既包含了方差也包含了偏差,能够很好地度量估计性质:积分均方误差越小说明估计性质越好.
通过变量代换和r次分部积分可以得到核方法下导数估计的偏差和方差[3],从而积分均方误差为

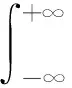
通过使积分均方误差达到最小,得到密度函数各阶导数的最优带宽为
h=Cr,v(k,f)n-1/(1+2r+2v),Cr,v(k,f)=R(f(r+v))-1/(1+2r+2v)Ar,v(k),
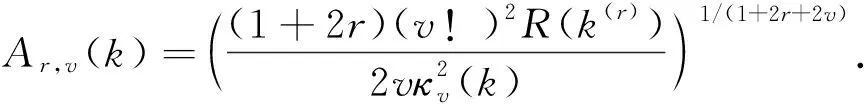
通过上述结果可以看出,密度函数导数核估计使用的最优带宽为O(n-1/(1+2r+2v)),而密度函数使用的最优带宽为O(n-1/(1+2v)).这是因为光滑估计的最优值取决于估计对象和分析目的,故估计的均方误差会发生变化,最优带宽也会随之发生变化[16].
到得草原中来,绿色王国,花草天堂,但在漫无涯际之中,此番我的观光焦点,不全在草原山岗河流等大景致,反而破天荒地“微观化”了。
引理1假定密度函数f(x)至少r+v+1阶可导,核函数满足k(s)(∞)=0,k(s)(-∞)=0,s=0,1,2,…,r,h→0,当n→∞时,nh→∞,则核方法的渐近偏差与渐近方差分别为
引理2满足假定1和假定2,2≤r≤p,h→0,当n→∞时,nh→∞且nh2p+1=O(1),则局部多项式回归方法的渐近偏差与渐近方差分别为
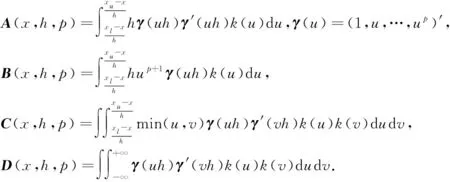
因为满足林德伯格条件[17],所以由林德伯格-莱维中心极限定理可得:核方法和局部多项式回归方法下估计的概率密度导数服从渐近正态分布,关于更加细致的证明详见参考文献[4,9].
核方法估计密度导数的渐近偏差与渐近方差的证明过程详见文献[4],局部多项式回归方法估计性质的证明在Cattaneo和Jansson (2019)中有详尽的叙述[9],这里仅对结果进行分析. 从式子上看,核方法与局部多项式回归方法下的估计偏差与方差并不能合理比较,因此在第2节中,通过数值模拟结合实际比较二者的估计性质.
2 数值模拟
本节通过数值模拟的方式,以密度函数的一阶导数估计为例,分别采用核方法与局部多项式回归方法估计,对比同一分布下2种方法的经验均方误差,并且直观呈现密度导数估计结果[13].
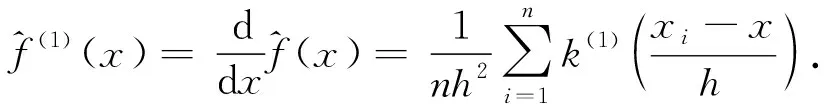
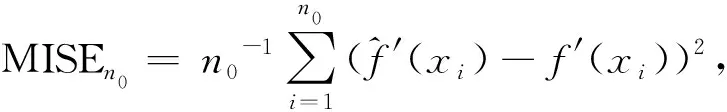
2.1 均匀分布
从图1可以看出,在样本量一致的情况下,无论使用哪个包估计,局部多项式回归方法的估计积分均方误差始终小于核估计的误差,故对导数估计,局部多项式回归方法优于核方法. 横向比较趋势,局部多项式回归方法随着样本量增加,均方误差存在大幅度或小幅度的减少;而核方法的两个估计结果却越来越差. 在不同样本量下,lpdensity包的经验均方误差值最小,且随着样本量增加,该估计的均方误差越来越小,即大样本量下,会有更小的均方误差. 此外,通过图2,可以看出在4个软件包中,lpdensity的估计结果最接近于真实值0. 虽然局部多项式回归方法在边界处的估计仍存在进步空间,但相较于核方法在-1和1附近的估计结果,局部多项式估计的表现还是明显更优的. 局部多项式对内点的估计效果也优于核估计.

图1 均匀分布导数估计的均方误差
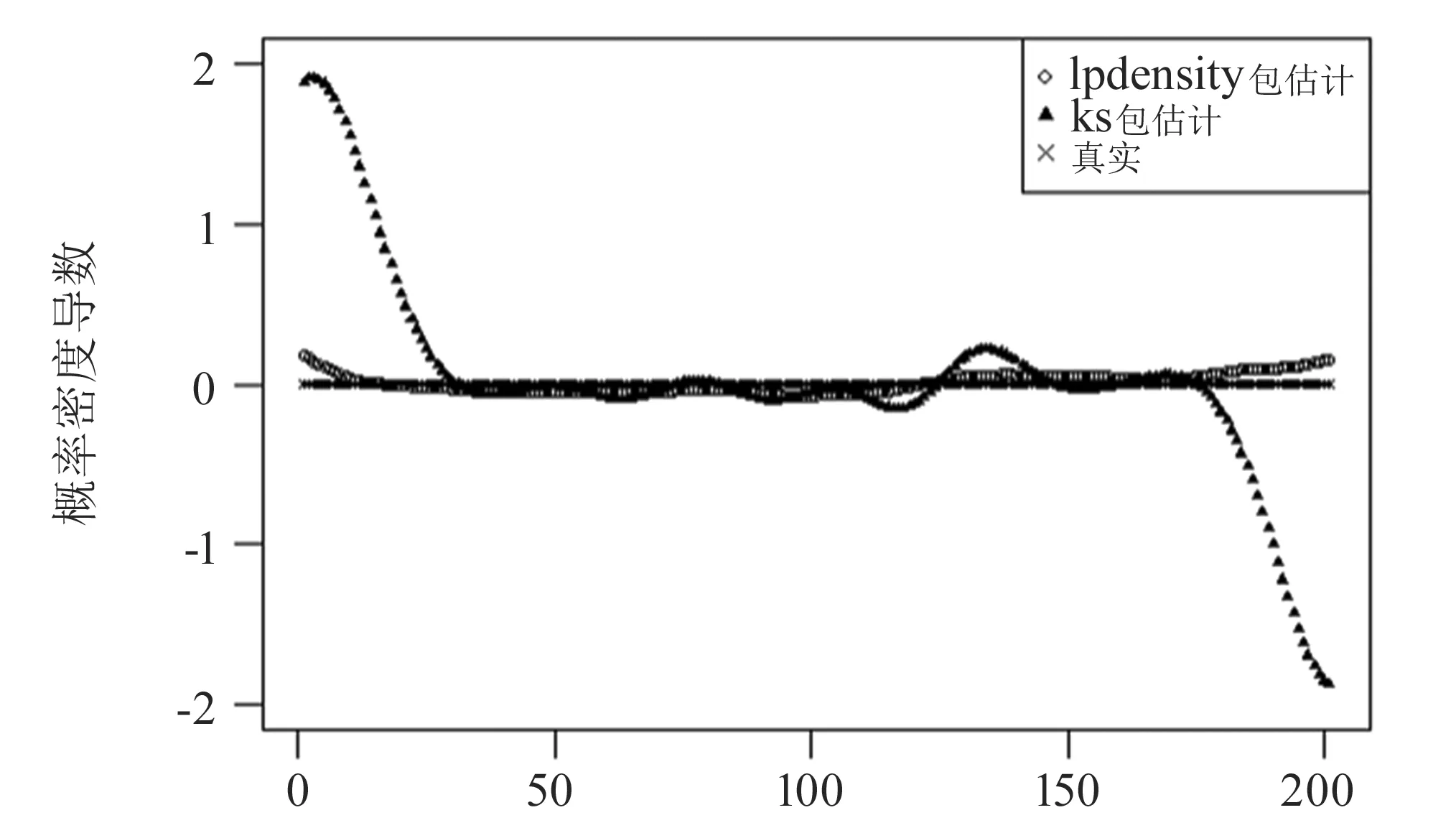
图2 均匀分布导数估计结果
2.2 正态分布
采用核估计方法和局部多项式估计方法,选择均值为0,方差为1的正态分布进行100次数值模拟,给出样本量为2 000时,呈现两种方法中最优的估计结果见图3和图4.

图3 正态分布导数估计的均方误差
横向比较图3,当样本量逐渐增大,4个软件包下的估计均方误差均存在减小的趋势,即局部多项式回归方法和核方法的估计效果越来越好. ks的估计均方误差随着样本量增加越来越接近0,在图4中的估计结果也十分优秀. 可见对正态分布来说,合适的核方法可以得出较好的估计. 每种样本量下,局部多项式估计的两个包的MISE虽然不是最优,但也不是最差. 另外,由于KernSmooth包locpoly函数的带宽需要提前设定,这可能导致了经验均方误差有小幅增加. 通过图4可以看出在正态分布的密度导数估计中,ks包中的kdde函数在边界附近和内点的拟合均明显优于lpdensity的估计. 虽然lpdensity的表现并不最优,但得到的估计曲线较为光滑,趋势也接近真实概率密度导函数.
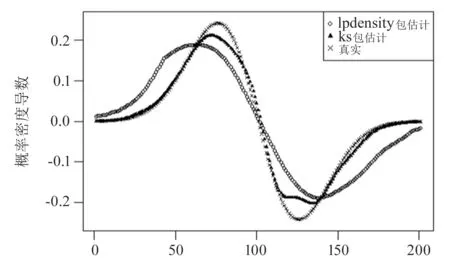
图4 正态分布导数估计结果
2.3 卡方分布
以卡方分布作为偏态分布的代表,对χ2(2)进行100次数值模拟,两种方法下的经验均方误差结果和样本量为2 000的估计结果与真实值,见图5和图6.
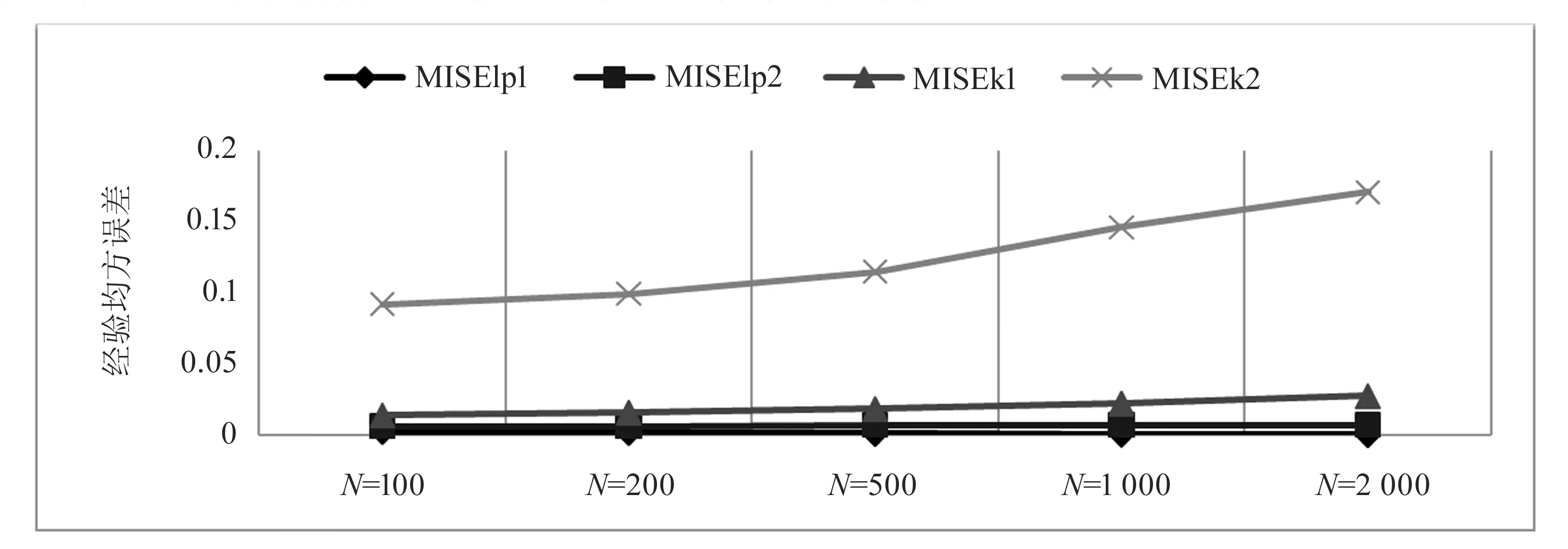
图5 卡方分布导数估计的均方误差
从以上结果可以清晰地看出偏态分布下,局部多项式估计依然优于核估计. 图中的数值趋势与均匀分布类似:无论在哪个包下,局部多项式回归方法的均方误差均小于核方法的均方误差;随着样本量增加,MISElp表现越来越好,估计结果越来越接近真实值,而MISEk却越来越大. 通过图6,可以直观看出核估计在边界处的估计结果与真实值的偏差较大,但局部多项式回归方法在0附近明显有更好的表现效果. 在内点,核估计出现了欠光滑,但局部多项式估计几乎完全拟合真实密度导数,估计性质十分优秀.
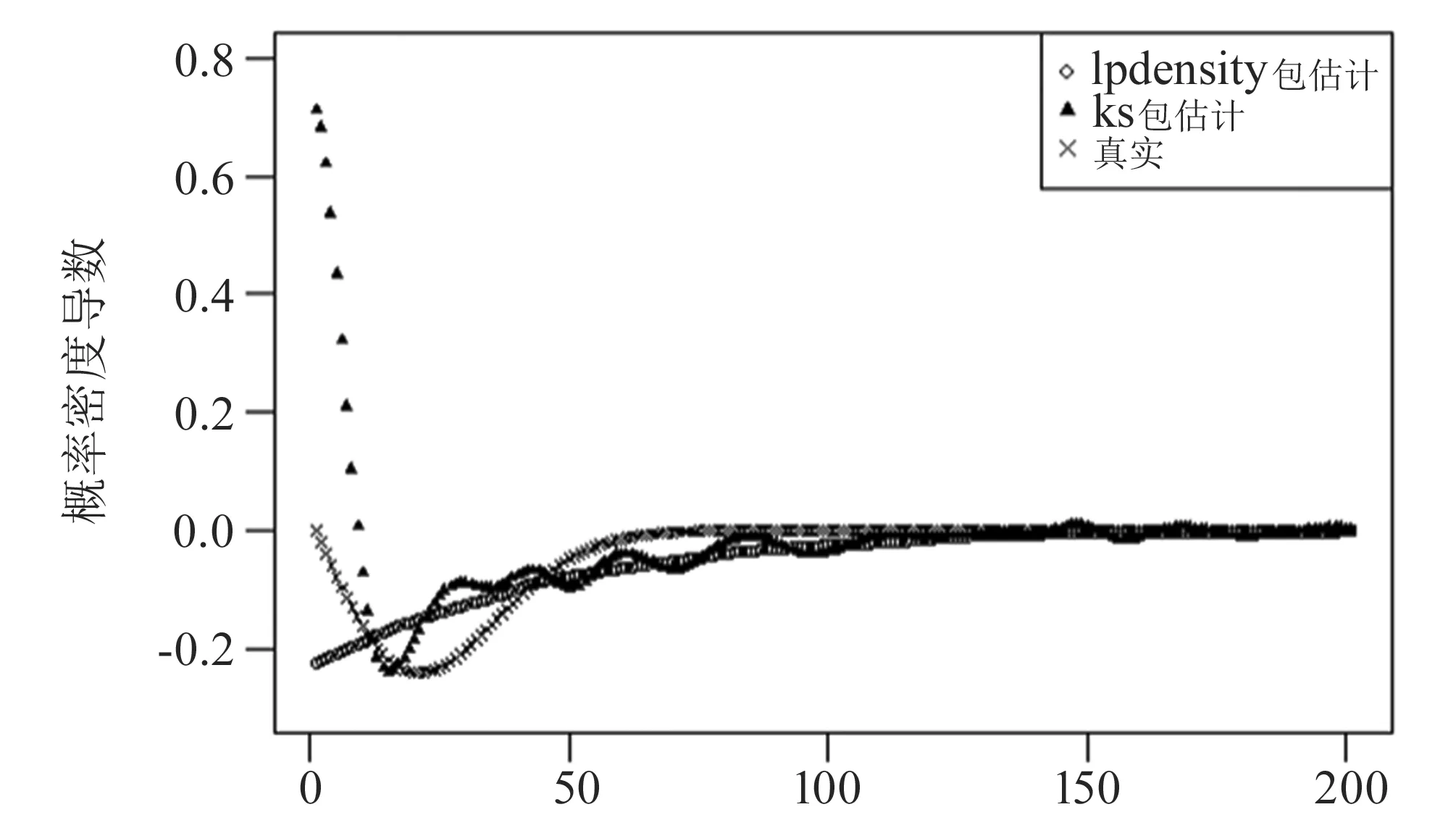
图6 卡方分布导数估计结果
2.4 小结
对比3个分布下的估计结果图,lpdensity对卡方分布的密度导数估计最优,其次是均匀分布,正态分布. 虽然在正态分布下,ks的估计在边界点和内点更胜一筹,但局部多项式估计方法在这3种分布下一直表现良好,说明该方法不仅有边界自适应性,还具有稳健性. 核方法在均匀分布和卡方分布的估计均方误差较大,这说明核方法不具有稳健性. 当分布未知时,核方法并不是最优选择. 正态分布下,ks包估计效果优于lpdensity. 但在其他两个分布下,ks的估计效果并不好,而且与事实相悖:随着样本量增加,均方误差却存在或大或小的增幅. 这可能与软件包的内置函数有关,不同R包的最优适应范围不同,为了更好地适应某类数据需要做出适当调整. 另外,ks包可以用于1至6维数据,在多维数据中也许会具有一定的稳健性.
通过观察数值模拟得到的3个均方误差图以及估计结果对比图,可以得到以下两个结论.
第一,由于正态分布的取值范围是全体实数,局部多项式回归方法在边界点拟合效果并没有完美体现. 但另外两个分布存在明确的边界,并且相对于核估计,局部多项式估计更接近真实值. 即在一般情况下,局部多项式估计具有边界自适应性.
第二,虽然局部多项式回归方法在正态分布密度导数下的估计性质不是最优,但这并不能否定该方法在另外两个分布下的良好表现. 即在大多分布下,相较于核方法,局部多项式估计方法更稳健、高效.
3 讨 论
本文基于核方法和局部多项式回归方法,得到概率密度函数的导数估计,并通过数值模拟对比两种方法下的估计性质,最终得到结论:样本量一定时,相较于核方法,无论分布为均匀、正态还是偏态,局部多项式回归方法的估计性质均更加优良. 局部多项式回归方法无需任何复杂的数据预处理就可以减轻边界偏倚并且具有边界自适应性、估计性质稳健等优点. 此外,该方法的理论体系愈见成熟,各阶导数估计偏差和估计方差的计算和证明也都有着系统的阐述. 为了进一步对比核方法和局部多项式回归方法,在第二部分以均匀分布、正态分布和卡方分布为例,在不同样本量下采用两种方法估计概率密度函数的一阶导数,分析对比了均方误差和各个点上的估计结果. 从数值与图形两个方面,验证了局部多项式回归方法不仅在内点的估计性质优越,在边界上的估计效果也十分良好,整体估计效果明显优于核估计. 在估计密度函数的导数时,该方法会更加稳健、高效、简单. 此外,局部多项式估计不仅可以应用在操纵检验中[10],还可以应用到极小化算法中[18],这会使检验结果与算法应用更加精准有效.
在导数估计中,本文仅讨论了一元局部多项式回归模型和核方法的估计性质,未比较两种方法在多元情形下的效果,这一比较会更加复杂. 另外,因为带宽选择对最终估计结果具有显著影响,所以这将会是另一个有意义的研究课题. 在统计推断方面,关于局部多项式回归的置信带也是一个不错的探索方向.

