高校图书馆中的一类优化问题及其求解算法*
张善美, 王志尚
(①曲阜师范大学图书馆;②曲阜师范大学管理学院,276826,山东省日照市)
0 引 言
在高校图书馆中,一些问题与稀疏性有着直接的关系. 例如,对于大数据时代产生的海量的电子资源, 迫切需要高效的方式来对海量数据进行存储、发送以及加密处理. 传统的存储方法已经满足不了新时代图书馆的信息知识爆发式的增长,我们需要寻求和探索如何使用较小的成本,在有限的空间中存储更多的资源. 在文献[1]中,作者基于智能化图书馆背景提出了一种压缩存储方法,首次尝试将压缩传感技术(通过利用信号、信息的稀疏性,大大提高信号采集能力、信息处理能力,缓解海量数据的采样、存储、传输和分析负担)应用于图书馆的数字资源管理中. 这对图书馆馆藏中电子资源的存储,尤其是非文本资源(诸如PDF 版本、JPG 版本、PNG 版本)的存储有着重要的意义,甚至对于高维度的影像以及视频的存储都起到重要的促进作用. 另外,高校图书馆作为信息资源的集散地,在不断满足科研学者的信息需求的同时,也存在着信息量庞大和用户特定需求难以匹配的矛盾. 这时就需要图书推荐系统发挥出其作用,使得图书馆资源得到充分利用. 虽然图书馆的个性化推荐系统在图书馆已经得到应用且为用户带来了一定的便利,也在一定程度上提升了图书馆的服务质量,但是由于没有较高的用户评价主动性,使得数据出现稀疏性问题[2]. 面对数据的稀疏性问题,我们如何来处理,才能得到最优的方案呢?本文研究与稀疏有关的一类最优化问题——稀疏优化.
考虑如下稀疏优化问题
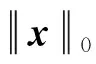
这类问题是由国际著名优化专家Amir Beck等在文献[3]中提出,此问题的特例之一就是著名的压缩传感问题. 由于其中涉及到的稀疏集合Cs={x∈Rn|‖x‖0≤s}是非凸的,这增加了求解此问题的难度. 文献[3]提出了经典的迭代硬阈值(IHT)算法. 该算法是传统梯度投影算法的一种推广,方向取负梯度方向,步长取1/L(L>Lf,Lf为目标函数梯度的Lipschitz常数). 该算法由于其良好的恢复性能,得到了大家的广泛关注. 但由于该算法取固定步长,且步长较小,会导致算法在迭代过程中下降速度很慢. 为改进IHT算法下降速度慢的不足,Pan等人提出了带有Armijo步长的IHT算法[4],该算法将IHT算法中的固定步长改进为Armijo步长规则来确定,算法所得迭代点的目标函数都能单调下降. 但是,正如在文献[5]中作者指出的那样,迭代序列有可能会陷入一个非常狭窄和曲折的“山谷”附近,从而产生非常短或曲折的步长,在这种情况下大部分的经典单调线性搜索技术可能会失效. 由此可见单调线性搜索并不能很好的解决所有的问题. 我们通常使用“非单调线性搜索”来解决这一难题. 非单调线性搜索,顾名思义就是,不是一味地减小函数的值.当遇到上述情况时,非单调线性搜索偶尔会増加目标函数的值. 函数值的増加可以使迭代序列走出这些“短或曲折的步长”的困扰. 因此,非单调线搜索不仅可以提高算法的收敛速度,还能増加找到全局最优解的可能性.
在本文中,利用IHT算法的基本思想,迭代方向取目标函数的负梯度方向,而步长采用了一种非单调线性搜索技术来确定. 这样做使得步长的选取有了更大的灵活性.
1 定义及预备知识
定义1.1[6]设Ω为非空闭凸集,对任意向量x∈Rn,称PΩ(x)=argmin{‖x-y‖:x∈Ω}为x到Ω上的投影.
定义1.2[3]称由Rn往稀疏集Cs上的投影为支撑映射,记为PCs(x).
由投影定义,PCs(x)应包含x中s个绝对值最大的分量和其余n-s个0. 对向量x∈Rn和i∈{1,2,…,n},我们用Mi(x) 代表向量x中按绝对值由大到小排列的分量,即
M1(x)≥M2(x)≥…Ms(x)≥…≥Mn(x),
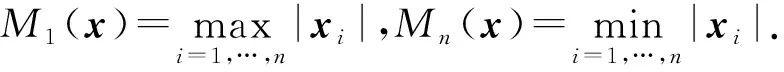
PCs(x)={y∈Rn|yi=xi,i∈Is(x);yi=0,i∉Is(x)}.
因为Cs是非凸的,所以投影PCs(x)并不一定是唯一的. 当Ms(x)=0 或者Ms(x)>Ms+1(x) 时,PCs(x) 是唯一的. 否则

如果存在两个及以上xi使得|xi|=Ms(x), 那么可以随意的选取或者根据已经定好的规则选取,其他取零.
引理1.1[7](下降引理) 若函数f是一个连续可微函数,且其梯度是Lipschitz 连续的,Lipschitz 常数为L,则对任意l′≥L,有
f(x)≤hl′(x,y) ∀x,y∈Rn,

定义1.3[3]设x*是一个可行点. 若存在α>0,使得x*∈PCs(x*-α∇f(x*)). 则称x*是一个α-稳定点.
引理1.2[3]对α>0,x*是一个α-稳定点当且仅当‖x*‖0≤s,且
Amir Beck等在文献[3]中提出了IHT算法来求解稀疏优化问题,该算法采用固定步长,利用梯度投影来进行计算,其算法如下.
算法1.1(IHT算法)
输入:常数L>Lf.
初始步:取x0∈Cs.
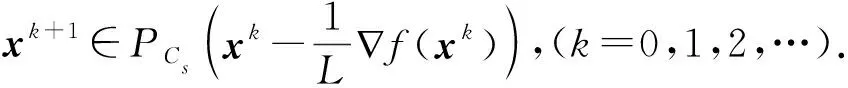
注1.1上述算法中的Lf为目标函数梯度的Lipschitz常数.
引理1.3[3]设{xk}k≥0是由IHT算法生成的序列. 则
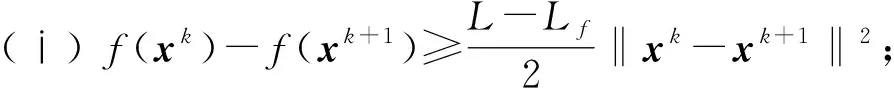
(ⅱ) {f(xk)}是一个不增序列;
(ⅲ) ‖xk-xk+1‖→0.
定理1.1[3]设{xk}k≥0是由IHT算法生成的序列. 则{xk} 的任意聚点都是α-稳定点.
IHT算法虽能保证算法在每一步都下降,但由于其取固定步长,不能保证每次迭代都有满意的下降量. Pan等人在IHT算法的基础上提出了带Armijo步长的IHT算法[4],该算法用Armijo步长代替固定步长,使目标函数在每一步有较大的下降量,其算法如下.
算法1.2
步骤1 计算xk+1∈PCs(xk-αk∇f(xk)),其中αk=α0γqk,qk是使得下式成立的最小非负整数
其中xk(α)=PCs(xk-α∇f(xk)).
步骤1.2 若‖xk+1-xk‖≤,停止;否则令k=k+1,返回步骤1.
定理1.2[4]设{xk}是由算法1.2生成的序列. 则有下述结论成立:
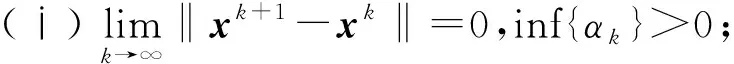
(ⅱ) {xk}的任意聚点都是α-稳定点.
2 算法及收敛性
下面采用非单调的Armijo线搜索来获得步长,以此来设计算法,得到算法2.1.
算法2.1
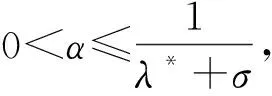
步骤0 选取x0=0,0
(2) 若
(3)
满足,则xk+1=u,转步骤2.
注2.1[k-M]+=max{k-M,0}.
(3) 置Lk=τLk,返回步骤1.
步骤2 若‖xk+1-xk‖≤,停止;否则令k=k+1,返回步骤1.
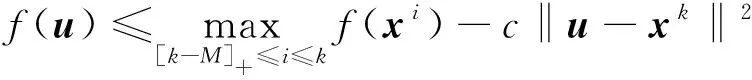


其中L是目标函数梯度的Lipschitz常数. 由投影算子的性质,
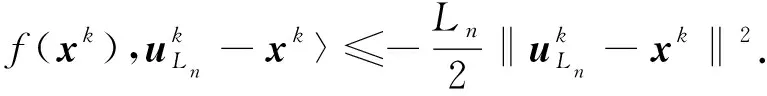
引理2.2设{xk}是由算法2.1生成的序列. 则有
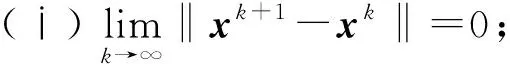
(ⅱ) {f(xk)}收敛.
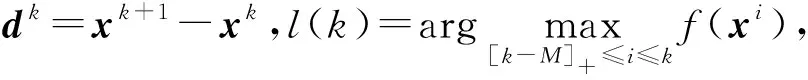
(4)
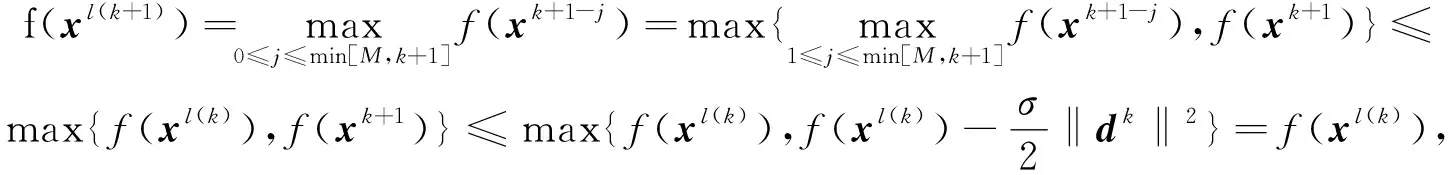
所以函数{f(xl(k))}是单调不增的.
又因为函数f(x)有界,不妨设
(5)
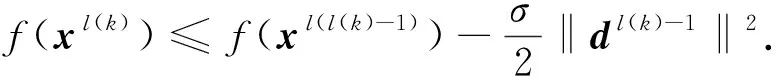
(6)
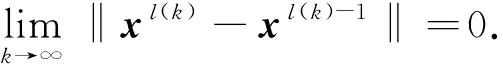
(7)
下面证明以下式子成立:
(8)
式(6)和式(7)证明了:当j=1时,上述两式成立. 由数学归纳法,只需证明对j(j≥1) 成立时,对j+1 也成立即可.

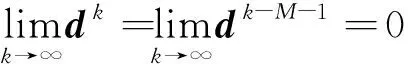
定理2.1设{xk}是由算法2.1生成的序列. 则{xk}的任何聚点都是α-稳定点.
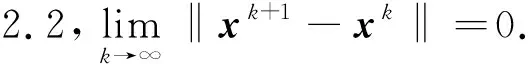
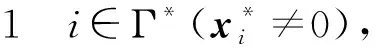
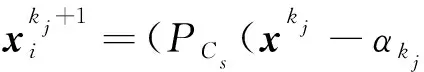
因为{αk}有下界,且下界大于零,两边取极限,则有
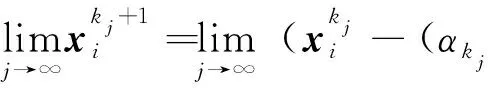
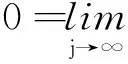
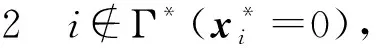


综上
这样,由引理1.2知,得到的聚点是α-稳定点.

