全同性粒子量子效应及应用*
秦玉娇, 王 宁
(①曲阜师范大学实验教学与设备管理中心,276825,山东省日照市;②广西师范大学-广西核物理与核技术重点实验室 ,541004,广西壮族自治区桂林市)
0 引 言
自普朗克提出量子概念以来,经过玻尔、玻恩与薛定谔等人的发展,量子力学体系不断得以完善. 20世纪早期,人们渐渐发现,假若原子的束缚电子数不是奇数而是偶数,则原子在化学上更为稳定. 里德伯在1914年建议,主量子数为n的电子层最多只能容纳 2n2个电子,但是他并不清楚为什么在表达式里会出现因数2. 泡利于1922年通过分析实验结果提出他的不相容原理:在量子力学里,所有同种微观粒子是不可分辨的,2个电子不能处于相同的量子态. 泡利在1925年的论文中并没有说明为什么自旋为半整数的费米子遵守泡利不相容原理[1].
全同性原理是泡利原理引申出来的,以算符和波函数知识原理为基础,从全同性原理的提出,全同性原理的应用和实验现象,说明全同性原理的重要性.
1 全同性原理的提出
内禀性质(质量、电荷、自旋、同位旋等)完全相同的粒子称为全同粒子. 与经典力学描述粒子运动用轨道不同,量子力学用波函数描述粒子的状态,粒子波函数以波包的形式逐渐扩散,当2个粒子的波包有重叠区域的时候,无法区分2个粒子,更无法编号,于是作为量子力学基本公设之一的全同性原理被提出,即当1个全同粒子体系中各粒子的波函数有重叠的时候,这些全同粒子是不可区别的,换言之,当波函数未重叠或距离较远时,是可以被区分的. 按照普朗克的说法[2],全同粒子具有相等性.
1.1 全同性原理与交换对称性
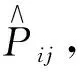
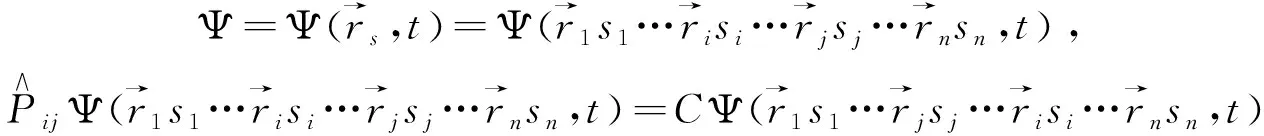
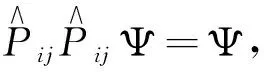
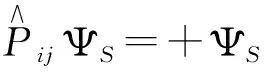
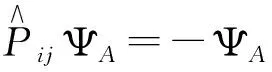
交换对称或反对称是全同粒子体系波函数固有的、特殊的性质,它决定了粒子所服从的统计. 实验表明,粒子的统计性与自旋有完全确定的关系,因此如果能知道统计分布,可以推导出粒子类型,为课题研究带来方便.
1.2 粒子统计性与自旋
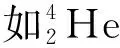
1.3 粒子统计性与时间演化
对于由N个全同粒子组成的体系,其哈密顿算符
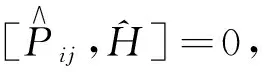
2 全同性原理在散射中的应用
2.1 散射原理
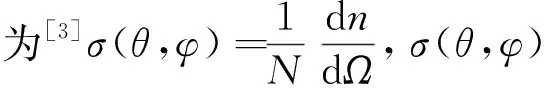
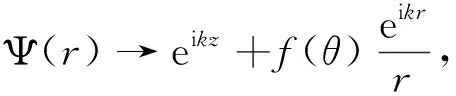
2.2 全同粒子散射
在重离子熔合过程中,需要探测器随时探测记录弾核或靶核的运动状态. 而对于全同性粒子,由于固有属性相同,探测器无法区分弹核或靶核. 研究较多的是在库仑势作用下,粒子的全同性与非全同性有所区别. 对于电子的运动,应包括自旋运动和轨道运动两部分. 为简便,对于全同性粒子,在不考虑自旋,只考虑空间相互作用,那么空间波函数满足对称性或空间反对称性,得到的散射截面分别可表示为
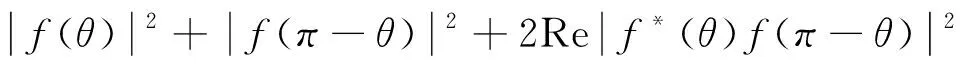
(1)
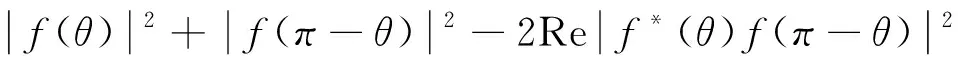
(2)
上两式前两项对应经典预期,后一项显示出量子波动性. 结合库仑散射公式,以α粒子为例,当其与重核碰撞,散射过程为卢瑟福散射,表达形式为(3),并由盖革-马斯顿实验证实
(3)
而对于自旋为零的情况下,α-α粒子散射满足空间对称,结合公式(1),其散射截面为
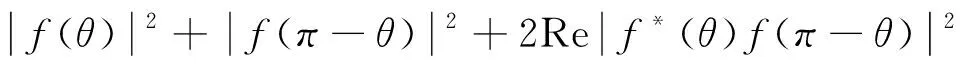
(4)
结合(3)与(4)发现,全同粒子散射与非全同粒子散射有较大的区别,全同粒子量子效应涵盖的信息较丰富. 因此对于较难合成的12C+12C体系,可能与全同粒子性有关.
当入射粒子自旋为1/2时,就不能单纯的使用卢瑟福散射公式,而是采用Mott(莫特)散射公式[4],假设入射粒子原子序数为Z,相对运动能量为E,其表达式可表示
(5)
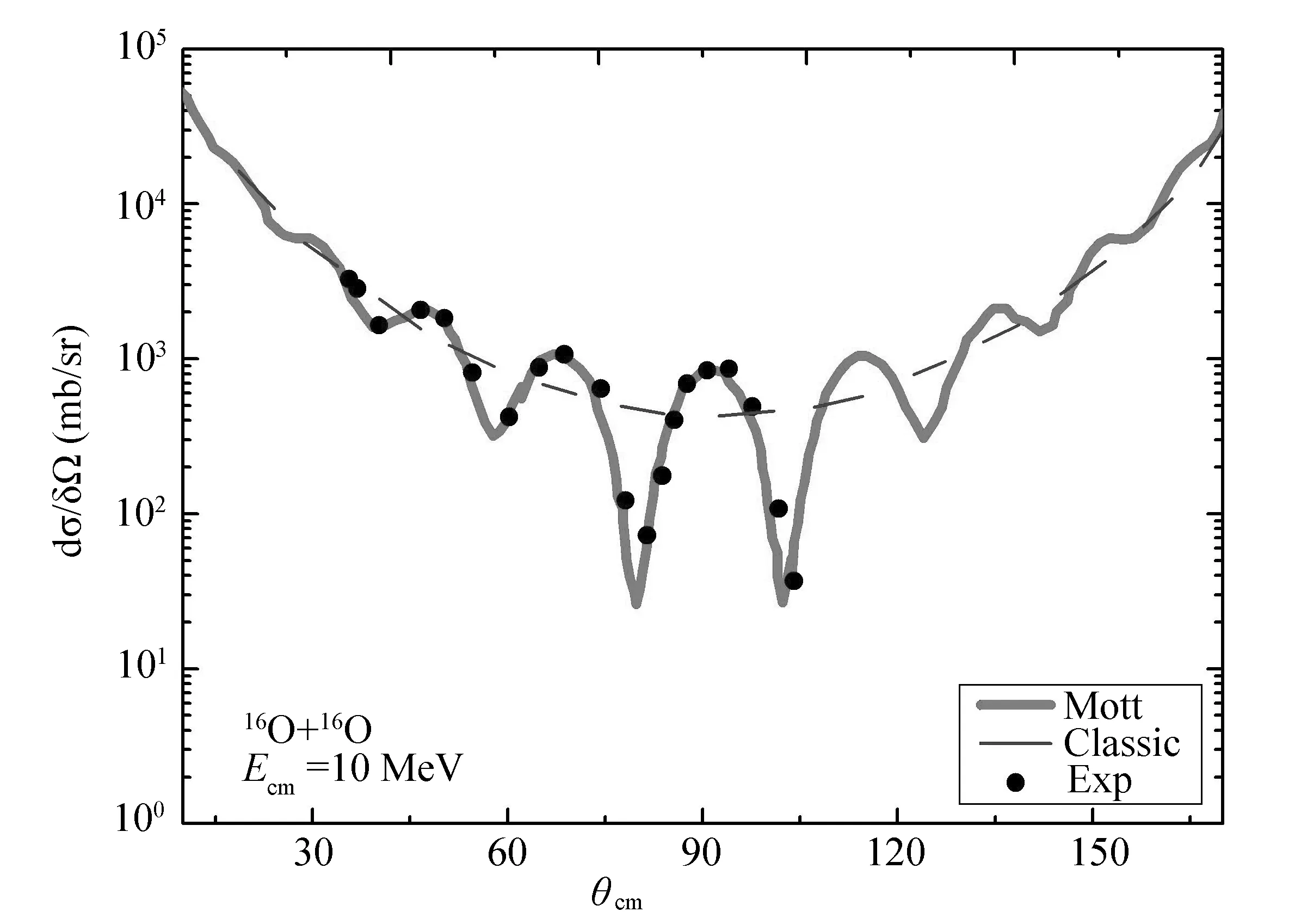
图1 Mott散射角分布
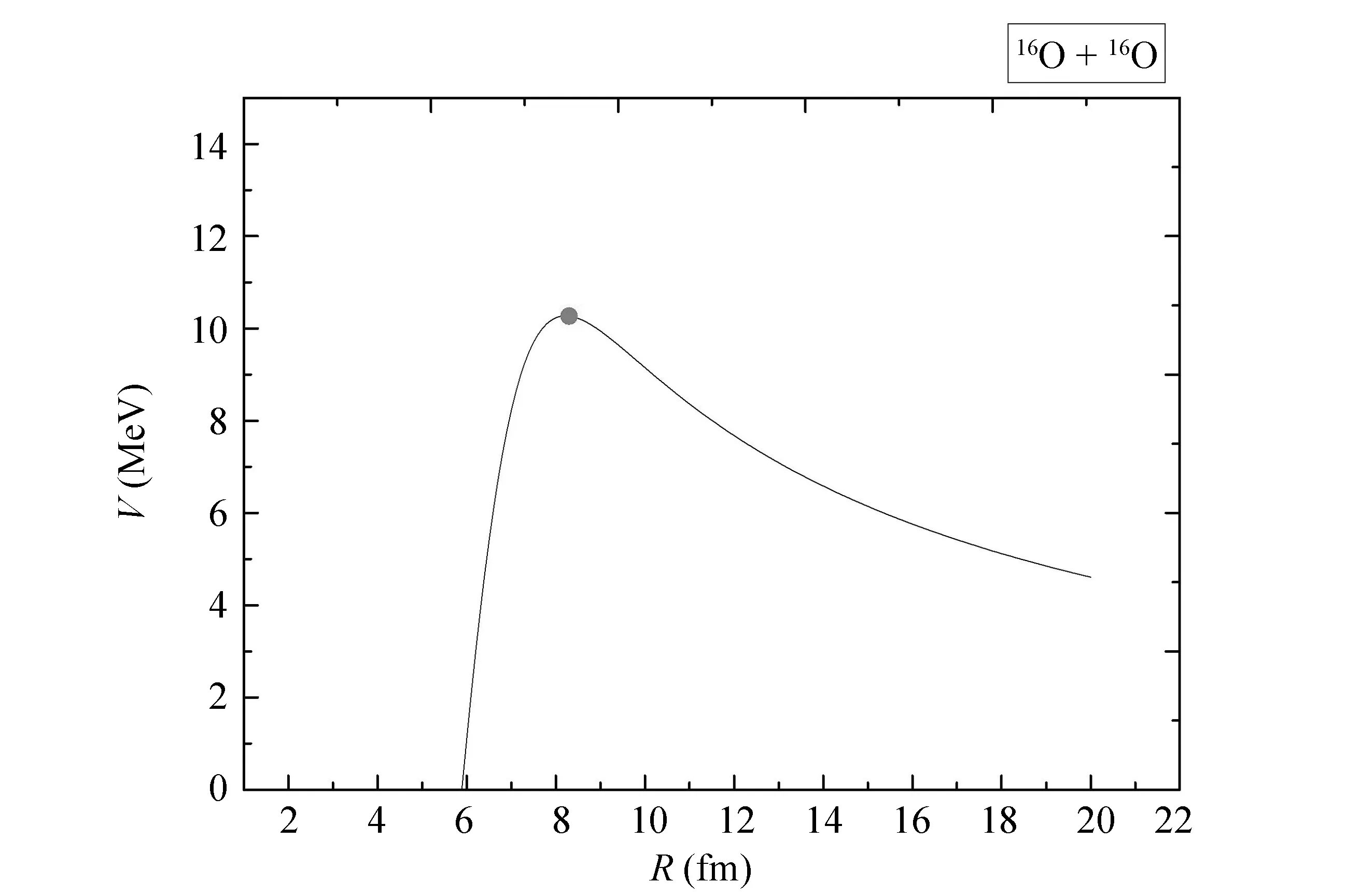
图2 16O+16O势垒分布
在公式(5)中,l表示原子核的自旋.
针对16O+16O体系,与经典相比,Mott散射可以很好再现实验数据,见图1[5],能够突出振荡,体现了量子效应.
通过将全同粒子散射与双缝干涉实验对比,王宁[6]等已发现对具有实验数据的对称体系碰撞,在散射角为90°附近会张开一定的角度Δθ,通过提取此角度可以得到势垒位置,这对于发现核子内部信息,提取势垒位置有较高的参考意义.
2.2.1 势垒位置确定

在此借助常见的重离子熔合反应势Bass80势[7],检验提取的位垒位置.
其中s=R-R1-R2,R表示熔合过程2原子核距离,R1和R2表示2核的半径,Z1和Z2分别代表原子序数.
当入射能量Ecm=10.5 MeV时,得到16O+16O体系势垒分布如图2.该处势垒高度VB=10.27±0.3(MeV),RB=8.2±0.42(fm),可见d与RB较接近,相比于传统的通过实验熔合截面提取位垒分布的理论模型,通过直接测量散射角度的方法计算位垒分布更简洁, 有较好的预言能力. 因此依据全同性粒子散射的角分布提取的最近距离对于检验模型理论的正确性有一定的参考价值,也有力证明了粒子的波动性.
2.2.2 位垒波动性解释
基于双缝干涉和单缝衍射的实验现象如图3,发现当双缝宽度a与缝间距b之间满足一定关系时,发现光屏上的明暗条纹并不是规律分布.会出现特定的缺级现象,缺级位置分布在b/a=n处.
因此,此处仍针对全同粒子的对称体系碰撞,当两核之间距离R与核子半径r也满足R/r=n(n为整数),应该有势分布的波动现象,此处针对40Ca+40Ca体系,在相同入射能量下采用不同的理论模型计算其在熔合过程中动力学势垒分布见图4,40Ca的原子核半径r=3.59(fm),标红对应位置R1≈3.67(fm),R2≈6.9,可见2核间距R1/r≈1,R2/r≈2,进一步显示出粒子波动的量子性.

图3 双缝干涉示意图 图4 40Ca+40Ca势垒分布
3 全同粒子交换能
由于全同粒子波函数满足的交换对称性与反对称性,使得空间波函数出现概率加倍或概率为0的情况,假设两全同粒子对称和反对称波函数为ψSA(r1,r2),那么
(6)
4 全同性原理在天体演化中的作用
对于较重的天体,从宏观上看当所受重力和压力不平衡时会存在塌缩现象,形成超密态的白矮星、中子星,从微观看是由于全同性粒子的存在和交换能的作用,使得玻色-爱因斯坦凝聚现象的产生,即在统计规律下大量粒子在接近绝对零度的温度环境中存在基态凝聚的现象,而在白矮星和中子星内部包含大量的中子或电子,内部温度T=107K,氦完全电离,这些中子的速率分布与自由电子在T=0 K时速率分布类似,因此会产生比较高的简并压强,这种压强即为费米压强. 设白矮星总质量为M,半径为R,则
M=(me+2mp)N≈2mpN,
(7)
(8)
产生的费米压强抵抗这种万有引力塌缩,而使得星体平衡. 简并压强表达式可表示为
(9)

综合表达式(8)(9)得到压强大小主要取决于N与V,这是费米-狄拉克统计在天体物理中的特别应用,对于探究星体演化、星体质量给出理论指导.
5 结 语
基于全同粒子及波函数特性,研究了全同性原理在散射、交换能以及天体演化中的的应用,全同粒子散射对于对称体系重粒子熔合,原子核裂变和极端垒下熔合机制的研究有较高的参考价值,基于双缝干涉和衍射图景,研究了对称体系熔合位垒分布波动现象,有力证明了熔合过程粒子表现的波动性,对于多种物理和化学统计稳定现象可给出合理解释.

