ATV模型的非线性多重网格法*

韩 粉， 杨奋林

(吉首大学数学与统计学院，416000，湖南省吉首市)

0 引 言

近年来，基于Lp范数的图像去噪模型[1-3]因能避免阶梯效应引起了众多学者的兴趣，此类模型算法的研究也成为了热点.考虑到梯度模不能有效区分图像边缘与斜坡，Chen设计了基于差分曲率的自适应全变分(adaptive total variation,ATV)模型[4]，并用显示梯度下降法求解此模型.显示梯度下降法采用负梯度方向为下降方向，原理简单且易于数值实现，但是由于算法的收敛需要的时间步长趋向于无穷小，导致了收敛速度缓慢.提高收敛速度的常见方法是对梯度下降方程采用隐式迭代或半隐式迭代.隐式梯度下降法能允许较大的时间步长且收敛速度快，但是算法的复杂度高.半隐式梯度下降法兼顾了显示梯度下降法与隐式梯度下降法的优点，既能允许较大的时间步长又能较快收敛，然而，虽然该方法前几次迭代误差会快速衰减，但是到解的附近时误差衰减缓慢.

为了加快ATV模型的求解速度，考虑到半隐式梯度下降法的收敛特点，拟用此方法设计光滑化方法，构造求解ATV模型的非线性多重网格法.

1 ATV模型

Chen设计的ATV模型[4]为

(1)

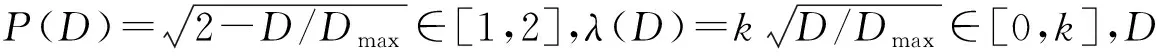
ATV模型不仅可以有效区分图像的边缘和陡峭的斜坡区域，而且能够在图像边缘和平坦区域自适应地选择合适的正则项，使得在有效去除噪声的同时兼顾保持边缘和避免阶梯效应.

(1)式的Euler-Lagrange方程为

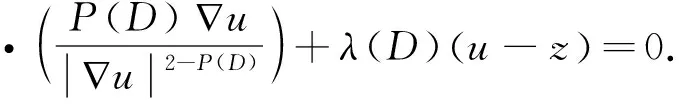
(2)

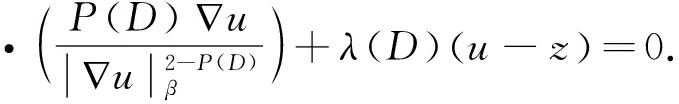
(3)

对(3)式的离散过程如下:

将图像域Ω=[0,n]×[0,n]剖分成n×n个小网格，令h表示沿x与y方向的网格步长，

(4)

则(3)式的离散方程组为

λi,j(ui,j-zi,j)=0，

整理得

(5)

其中

(6)

边界为

2.4 hsPDA组和nhsPDA组早产儿PDA导管直径情况 对hsPDA组及nhsPDA组早产儿PDA导管直径情况进行单因素分析：PDA导管直径1.5～3 mm与hsPDA相关联，两组差异有统计学意义(P<0.05)。PDA导管直径>3 mm与hsPDA无关联，两组差异无统计学意义(P>0.05)。见表4。

ui,0=ui,1,ui,n+1=ui,n,u0,j=u1,j,um+1,j=um,j.

(7)

记方程组(5)及边界(7)为

Nhu=λhz.

(8)

2 非线性多重网格法求解

若令时间步长t=1/10 s，仅使用半隐式梯度下降法求解(8)式，则前几次迭代误差会快速减小，然而随着迭代次数的增加，误差下降速率越来越缓慢.如图1所示，对像素为256×256、添加了标准差为10的噪声分布模型的Lena图使用半隐式梯度下降法后，第5次迭代相对误差小于5×10-4.

图1 Lena图相对误差下降曲线

非线性多重网格法被广泛地用于处理椭圆型方程组，现已具备了坚实的数学理论基础并在众多领域中取得了成功[8-10].该方法由前光滑、粗网格校正和后光滑组成，其基本思想是:先在细网格上通过前光滑求出近似解和误差，对误差和残量限制后进入套迭代，在最粗网格上求解残量方程得到误差，接着对误差进行插值，校正近似解并进行后光滑从而得到最终解.

考虑到非线性多重网格法[5-7]的光滑化方法不需要精确求解(8)式，只需要粗略地求出近似解，使误差经过几次前光滑或后光滑充分光滑即可，因而我们可以利用半隐式梯度下降法的前几次迭代误差会快速衰减的特点设计光滑化方法，构造求解(8)式的非线性多重网格法.在用非线性多重网格法求解(8)式前，先对网格进行标准粗化，即令h→2h，得到一系列粗网格上的图像域Ω2h,Ω4h,Ω8h,…,Ω2lh,l∈+.求解(8)式所用的网格间的转移算子为逐点限制算子逐点插值算子以及文献[11]中的full-weight限制算子与网格顶点的双线性插值算子，记它们为与所用的光滑化方法如算法1所示.

算法1光滑化方法：uh←S(uh,zh,Dh,t,iter)

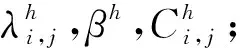
算法2非线性多重网格法：uh←NMG(uh,zh,Dh,k,β,t,v1,v2,iter)

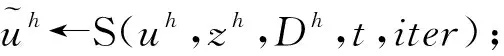
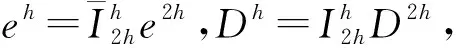
3 数值实验

选取像素为256×256的Cameraman图、像素为512×512的Lena图和Chili图作为测试图像检测不动点迭代(FP)法、半隐式梯度下降(SGD)法和非线性多重网格(NM)法的去噪效果.实验使用峰值信噪比(PSNR)和CPU计算时间定量分析这3种方法的性能，其中,PSNR越大表明去噪效果越好.

依次对Cameraman图、Lena图与Chili图添加标准差为10、10、20的随机噪声后，噪声图像的PSNR分别为22.544 8 dB，21.011 7 dB与20.430 3 dB.为了保证实验的公平性，合理的调整3种算法的参数使得每幅去噪后的图像的PSNR达到最大值.

表1展示了FP法、SGD法和NM法的去噪后的PSNR与CPU计算时间.由表1可知，FP法与SGD法去噪后的图像的PSNR相似，NM法的PSNR最大，约比SGD法的高1 dB；FP法的计算速度最慢，SGD法次之，NM法的计算速度最快，约为SGD法的2倍.

表1 3种算法去噪后的PSN和CPU计算时间

图2展示了对3幅噪声图使用FP法、SGD法和NM法的去噪效果.由图2可见，FP法与SGD法去噪后的图像有少量噪声残留，而NM法去噪后的图像更加清晰光滑.

(a) 原始图 (b) 噪声图 (c) FP法 (d) SGD法 (e) NM法

4 结 语

利用半隐式梯度下降法前几次迭代误差会快速衰减的特点，设计了光滑化方法，构造了求解ATV模型的非线性多重网格法.通过与FP法和SGD法的对照实验，表明新方法在去噪效果和收敛速度方面更好.为了进一步提高峰值信噪比和加快收敛速度，未来考虑从网格间转移算子的角度改进非线性多重网格法.