变质量力学系统的广义高斯原理及其对高阶非完整系统的推广1)
张 毅 陈欣雨
(苏州科技大学土木工程学院,江苏苏州 215011)
引言
高斯[1]于1829 年提出了一个微分变分原理,它是分析力学的普遍原理.陈滨[2]曾指出: “从力学概念上来说,把高斯原理作为基本原理似乎是最恰当的”.梅凤翔[3]认为“高斯原理可作为分析动力学的基础”.Udwadia 等[4]在他们的《分析力学》著作中以高斯原理作为出发点采用矩阵代数运算导出分析力学的基本方程及其对完整和非完整系统的应用,揭示了高斯原理在描述约束系统运动方面的广泛适用性.不同于d’Alembert-Lagrange 原理和Jourdain原理,高斯原理具有极值性质,可表示为拘束函数的高斯变分等于零[1].利用高斯最小拘束原理可以直接通过求函数极值的方法获得质点系的运动规律[5-6].因此,高斯原理在复杂系统的动力学建模以及近似计算等方面发挥其独特的作用.例如,机器人动力学[5]、多体系统动力学[6-14]、弹性杆动力学[15-18]以及混合动力学问题[19]等.梅凤翔等[20]对高斯原理的起源及其发展现状做了很好的综述.迄今,约束系统的高斯原理和最小拘束原理及其应用研究已有诸多成果[21-28].然而,尽管高斯原理在处理理想的一阶约束系统时是完备的[2],但是对于高阶约束系统,高斯原理及其极值问题仍是一个开放的课题.此外,在工程实际和自然界中存在大量变质量系统的实例[29-31],例如以喷射高速气流而实现高速运动的火箭、高空环境下工作的爬壁机器人、混凝土搅拌机以及喷淋系统等.近年来,在变质量系统的分析力学研究方面亦取得重要进展[32-38].本文将研究变质量力学系统的高斯原理.文中建立了变质量力学系统的高斯最小拘束原理,并通过定义变质量非完整系统修正的拘束函数,给出变质量非完整系统的高斯最小拘束原理;提出了变质量力学系统的广义高斯原理,通过定义广义拘束函数,建立了变质量力学系统的广义高斯最小拘束原理,并将方法推广到高阶非完整力学系统.
1 变质量力学系统的高斯原理
1.1 高斯原理
设变质量力学系统由N个质点构成,其位形由n个广义坐标qs确定.第i个质点的质量为mi=mi(qs,t),则Meщepcкий方程给出[39]

其中 δG(·) 表示高斯变分,即仅对加速度取变分,而坐标和速度不变[2].在高斯意义下,理想约束条件为
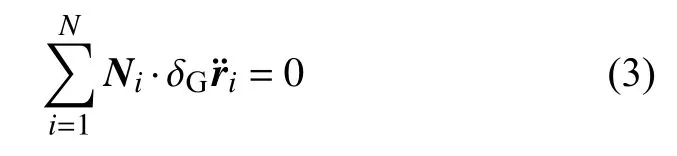
将式(3)代入方程(2),得
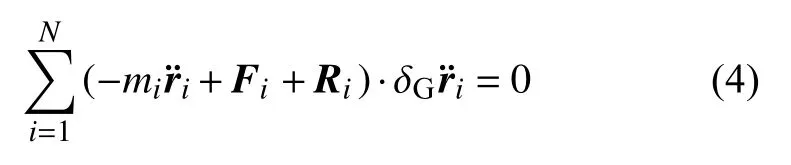
式(4)是变质量力学系统的高斯原理[39].
1.2 高斯最小拘束原理
高斯原理是建立在最小拘束概念的基础之上的.对于变质量力学系统,由于主动力Fi和反推力Ri不依赖于加速度,因此它们的高斯变分等于零.于是,原理(4)可改写为
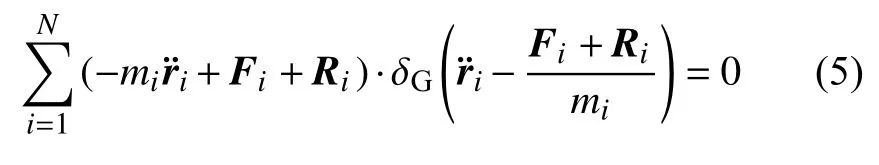
类似于常质量情形[1-2],定义变质量系统的拘束函数为
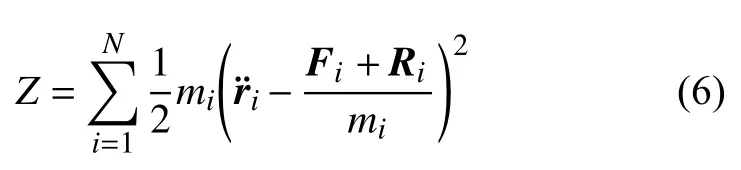
则式(5)成为

因此,式(7)表明: 对于具有双面理想约束的变质量力学系统,每一瞬时在其所有与约束相容的可能加速度之中,真实运动的加速度使拘束函数Z在高斯变分下取得极小值.因此,式(7)可称为变质量力学系统的高斯最小拘束原理.
如果系统中各质点的质量保持不变,则Ri==0,式(7) 给出经典的常质量情形下的高斯最小拘束原理[3].
将式(6)展开,得
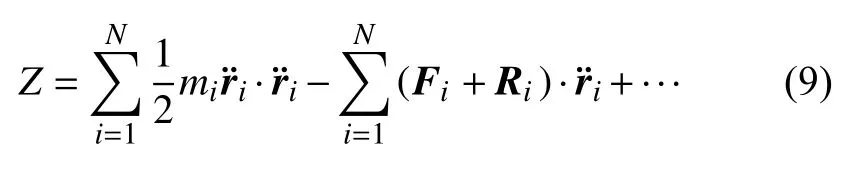
其中,省略号“···”表示与加速度无关的项.而
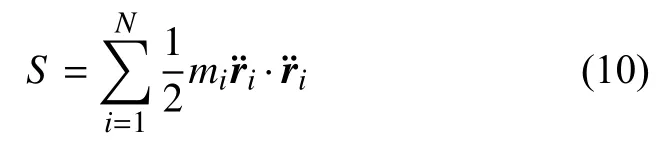
称为质点系的加速度能量[3].因此,拘束函数Z可表为
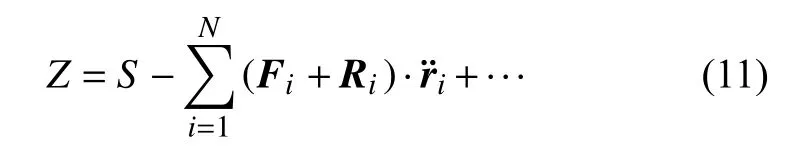
将点的矢径ri=ri(qs,t) 对时间t求二阶导数,得
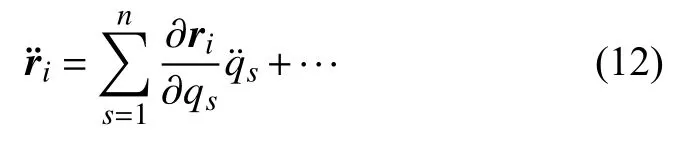
因此有

将式(11)求高斯变分,并考虑到式(13),得
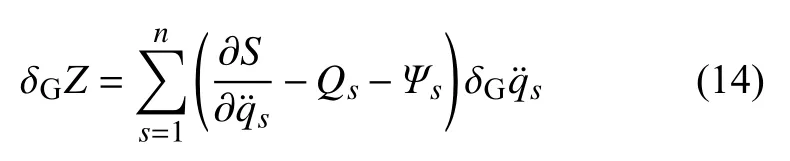
其中
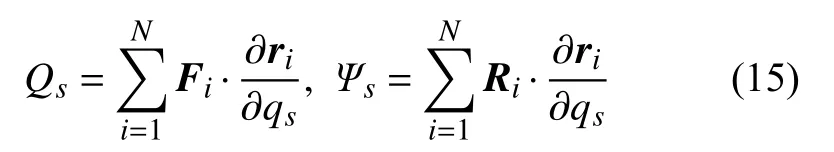
分别为质点系的广义力和广义反推力.于是,式(7)给出
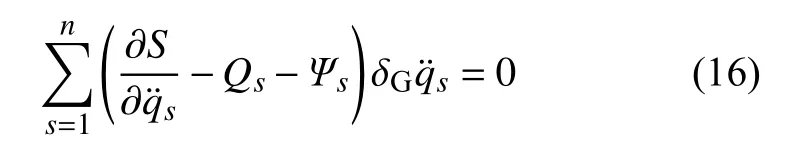
这是变质量力学系统高斯原理的Appell 形式[39].
1.3 高斯最小拘束原理对变质量二阶线性非完整系统的推广
假设系统受到理想二阶线性非完整约束
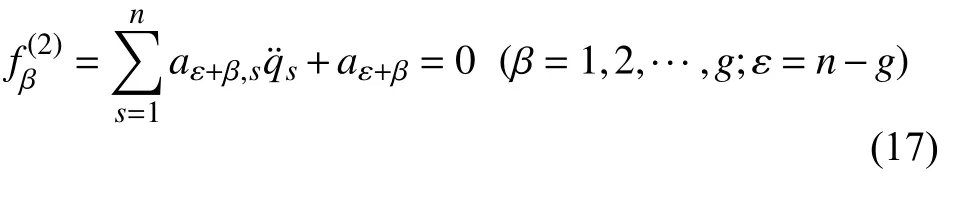
则约束加在加速度空间的虚位移上的限制为

其中aε+β,s和aε+β是广义坐标qs,广义速度和时间t的函数.
如果系统受到的是理想一阶非线性非完整约束
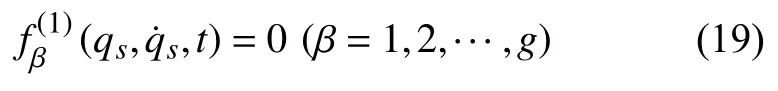
可将方程(19)求导,得
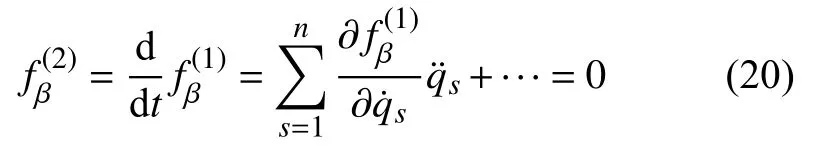
因此,比较式(17)和式(20),对于一阶非完整约束式(19),有
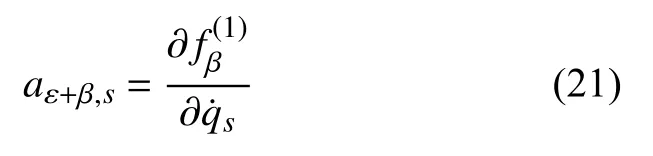
构造函数
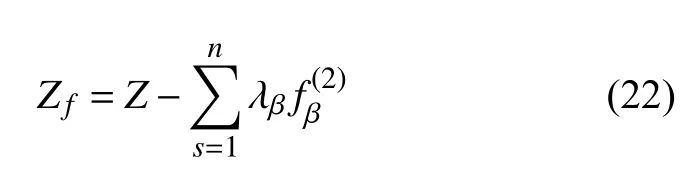
其中 λβ=λβ(qs,,t)是约束乘子.函数Zf可称为变质量非完整力学系统修正的拘束函数,等号右边第二项可视作由于存在非完整约束而对拘束Z的一个修正.将式(11)和式(17)代入式(22),得

容易证明

实际上,对式(23)求高斯变分,并注意到 λβ的高斯变分为零,我们得到
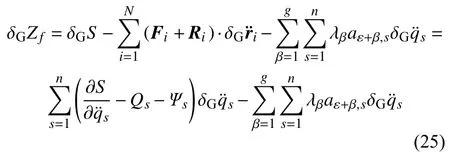
将式(16)和式(18)代入式(25),即得式(24).
类似于式(8),我们有
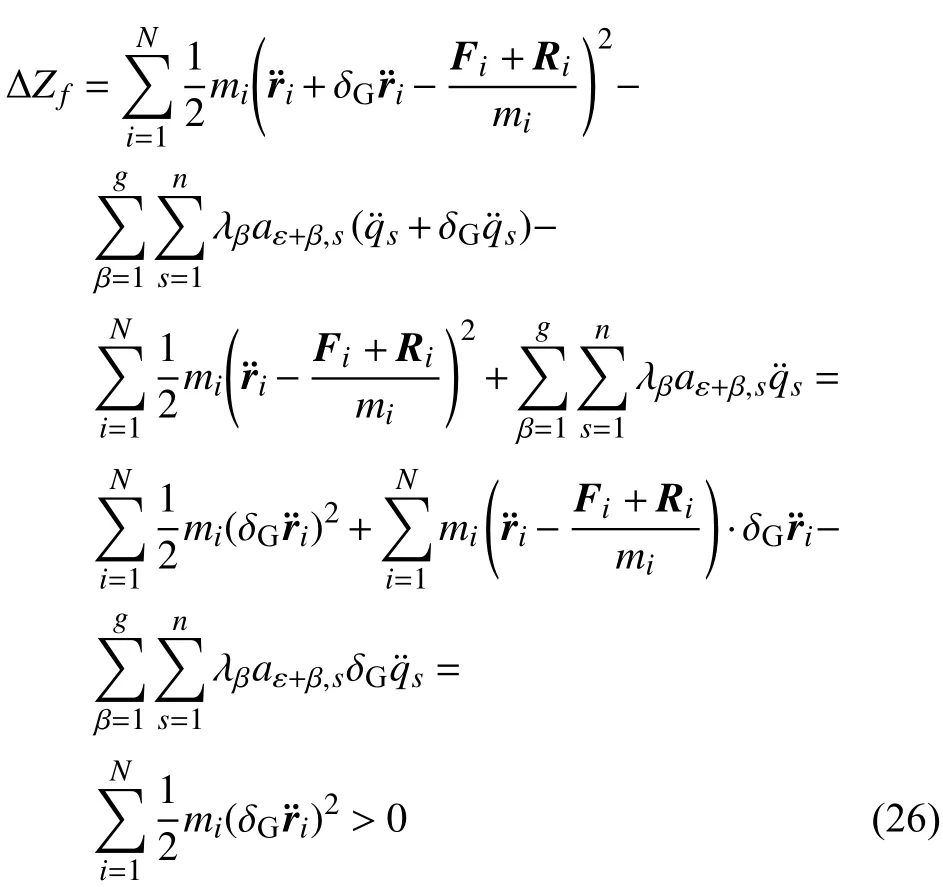
于是,式(24)表明: 对于具有双面理想约束的变质量二阶线性非完整力学系统,每一瞬时在其所有与约束相容的可能加速度之中,真实运动的加速度使修正的拘束函数Zf在高斯变分下取得极小值.式(24)可称为变质量二阶线性非完整力学系统的高斯最小拘束原理.
由式(25)和式(24)可表为
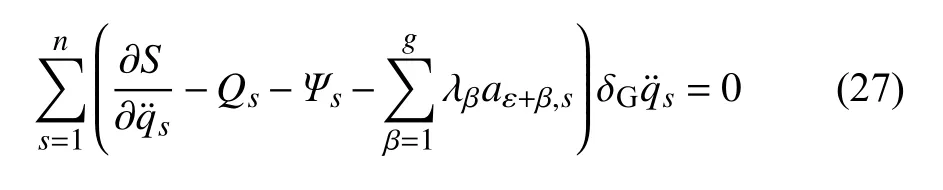
式(27)可称为变质量二阶线性非完整力学系统的高斯原理的Appell 形式.
2 变质量力学系统的广义高斯原理
2.1 广义高斯原理
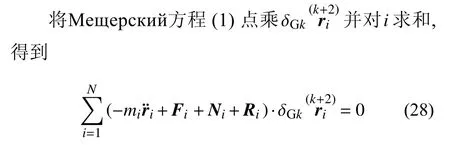
其中 δGk(·)可称为在k次加速度空间中高斯意义下的变分,或简称k次高斯变分,其变分规则为
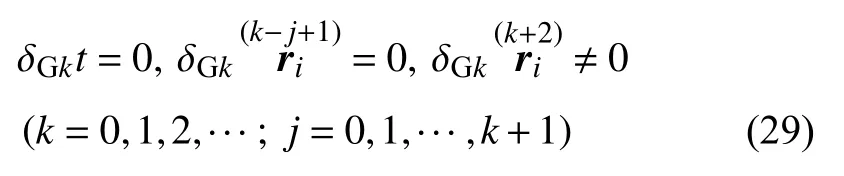
在广义坐标下的形式为
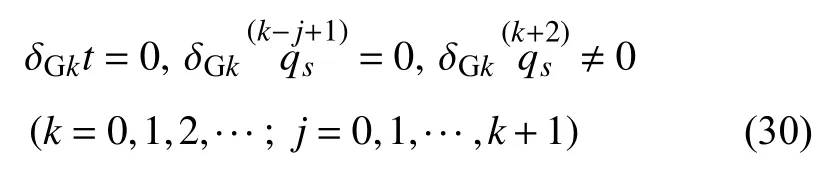
当k=0时,δGk(·) 成为经典的高斯变分.
在k次加速度空间,高斯意义下的理想约束条件为
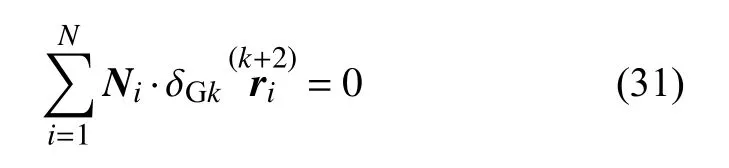
于是式(28)成为
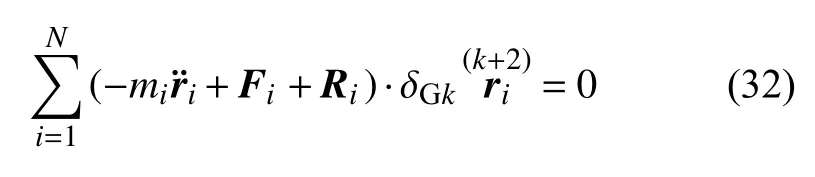
式(32)称为变质量力学系统的广义高斯原理,可表述为: 对于具有双面理想约束的变质量力学系统,在每一瞬时,真实运动不同于所有可能运动之处仅在于,真实运动使主动力、惯性力和反推力在k次加速度空间的任何虚位移上所做元功之和等于零.当k=0 时,式(32)退化为式(4).
若各质点的质量保持不变,则式(32)退化为
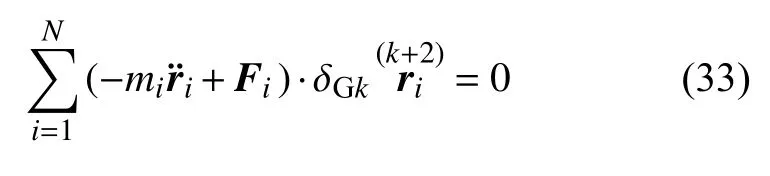
式(33)可称为常质量力学系统的广义高斯原理.
2.2 广义高斯最小拘束原理
将拘束函数(6)对时间t求k阶导数,并将其定义为广义拘束函数,即

于是式(32)成为

当k=0 时,式(36)成为式(7).
式(36)表明: 对于具有双面理想约束的变质量力学系统,在每一瞬时k次加速度空间所有与约束相容的可能加速度之中,真实运动的加速度使广义拘束函数Z~在k次高斯变分下取得极小值.式(36)可称为变质量力学系统的广义高斯最小拘束原理.
将矢径ri=ri(qs,t) 对时间t求k+2 阶导数,得
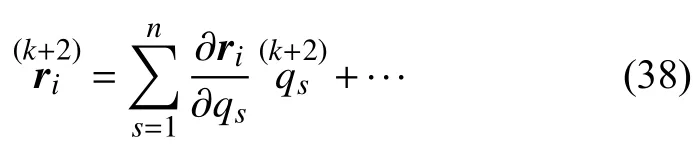
因此有
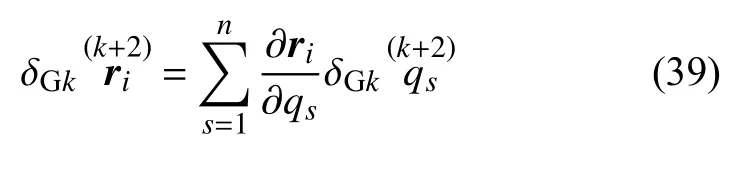
将加速度能量S对时间t求k阶导数,得到
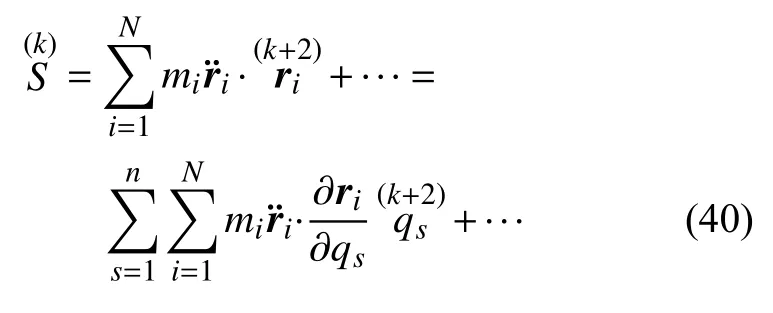
因此有
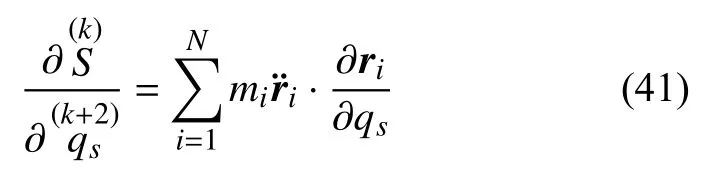
由式(39)、式(41)、式(35)和式(15),式(36)可表为Appell 形式
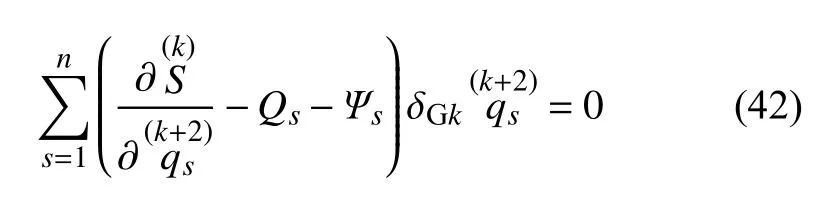
当k=0 时,原理(42)成为式(16).
若各质点的质量保持不变,则式(42)成为
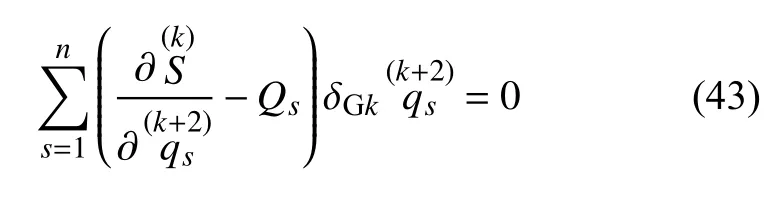
式(43)可称为常质量力学系统的广义高斯原理的Appell 形式.
2.3 广义高斯最小拘束原理对高阶非完整系统的推广
假设系统受有理想k+2 阶线性非完整约束
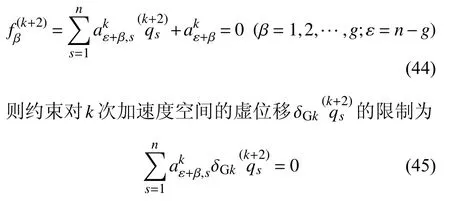

如果系统受到的是理想k+1 阶非线性非完整约束
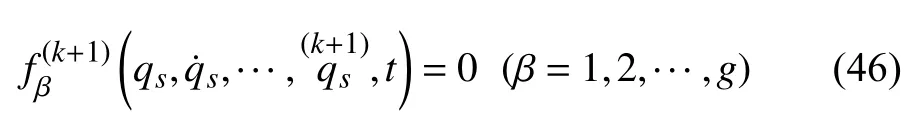
可将方程(46)求导,得
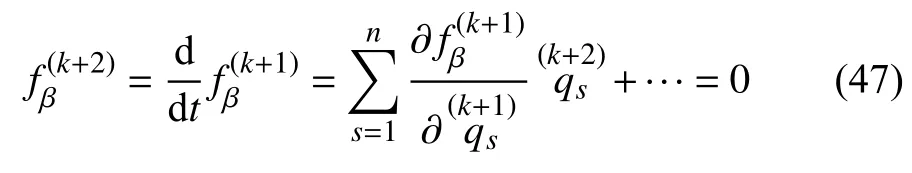
因此,比较式(44)和式(47),对于k+1 阶非线性非完整约束式(46),有
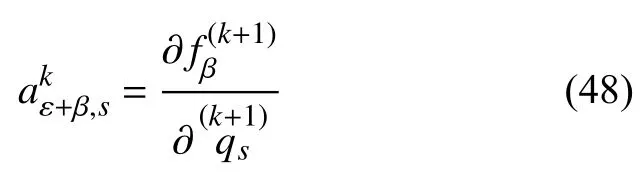
构造函数

将式(42)和式(45)代入式(51),得到

类似于式(37),我们有
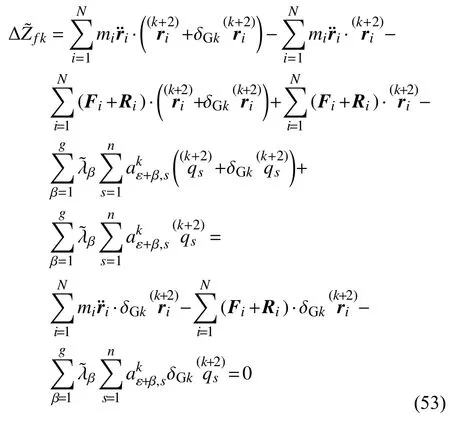
式(52)表明: 对于具有双面理想约束的变质量高阶非完整力学系统,在每一瞬时k次加速度空间所有与约束相容的可能加速度之中,真实运动的加速度使得广义拘束函数在k次高斯变分下取得极小值.式(52)可称为变质量高阶非完整力学系统的广义高斯最小拘束原理.
由式(51),式(52)也可表为
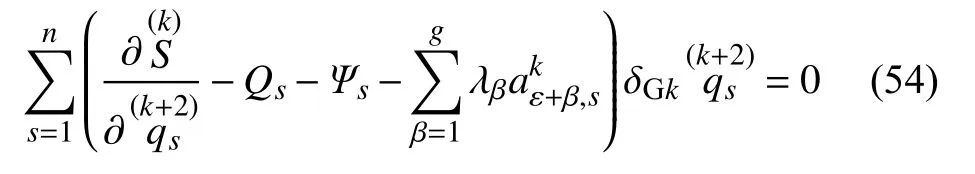
式(54)可称为变质量高阶非完整力学系统的广义高斯原理的Appell 形式.
3 算 例
例1.研究燃烧着的匀质圆球沿粗糙水平面的惯性运动.设球的初始半径为r0,密度为 ρ .试建立系统的运动微分方程.
解:设由于燃烧所引起的质量减少与球的表面积成比例,即[40]

取球心坐标x,y以及3 个Euler 角 ψ,θ,φ 为广义坐标,则球的加速度能可表为[40]

由于圆球沿水平面作惯性运动,且微粒分离的相对速度为零,因此广义力和广义反推力等于零.
圆球与粗糙水平面的接触点的速度等于零,即系统有2 个一阶非完整约束
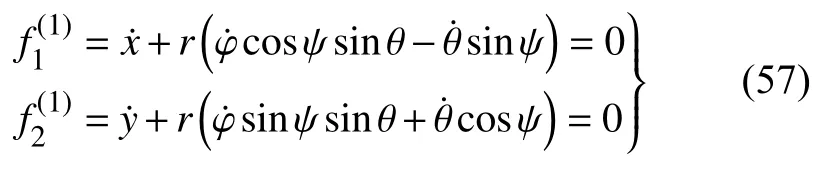
将式(57)对时间t求导数,得到
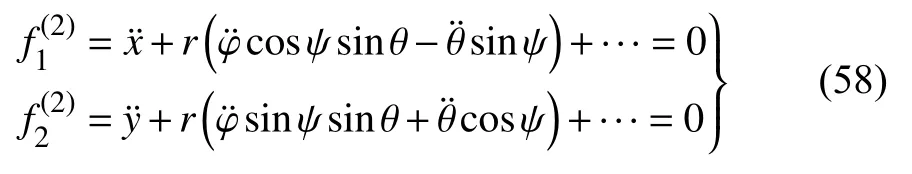
由本文给出的修正的拘束函数式(23),得到
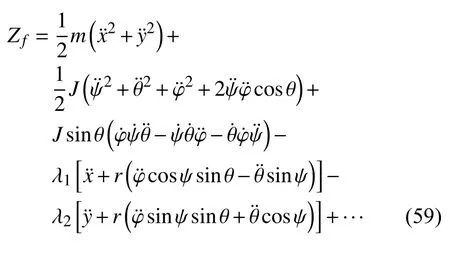
计算高斯变分 δGZf,并令其为零,得到
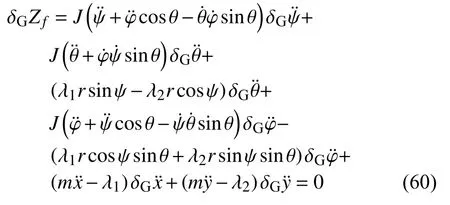
对于本问题,5 个广义坐标,2 个非完整约束,因此有3 个自由度.依据Lagrange 乘子法,由式(60)可得
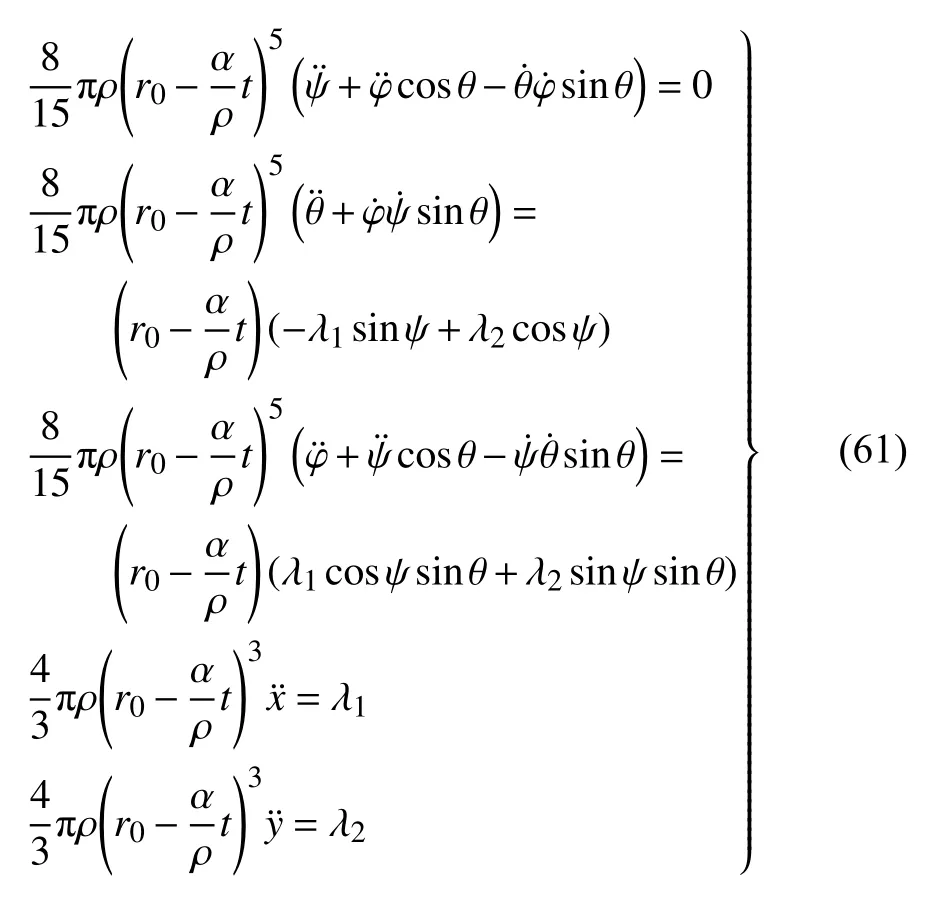
方程(61)是系统的运动微分方程,与文献[40]用Nielsen 方程给出的结果一致.
约束(58)对加速度空间的虚位移的限制为
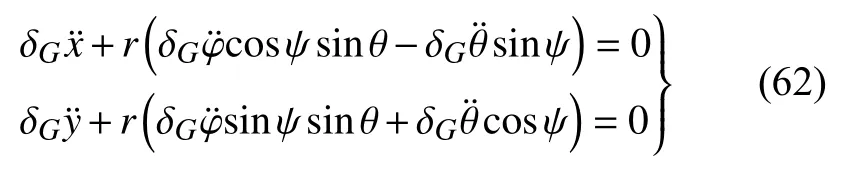
根据式(16),由式(56),可得
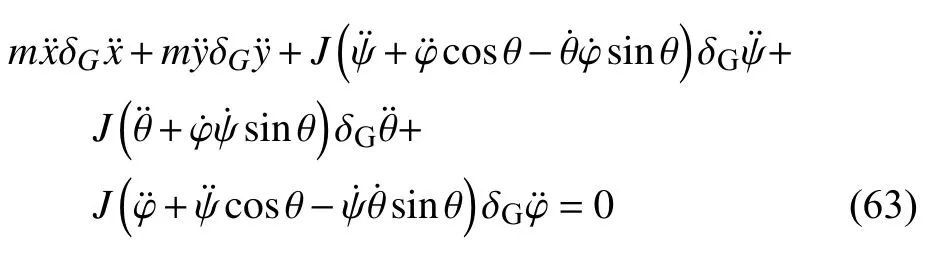
由式(59),系统的可能运动的拘束函数为
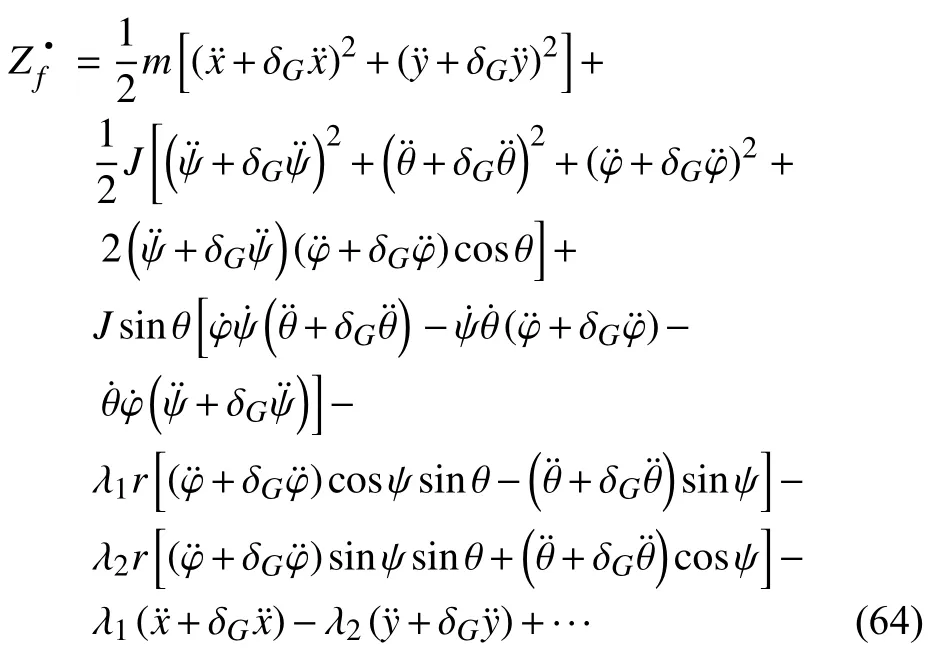
由式(64)和式(59),并利用式(62)和式(63),得到可能运动的拘束与真实运动的拘束Zf之差为
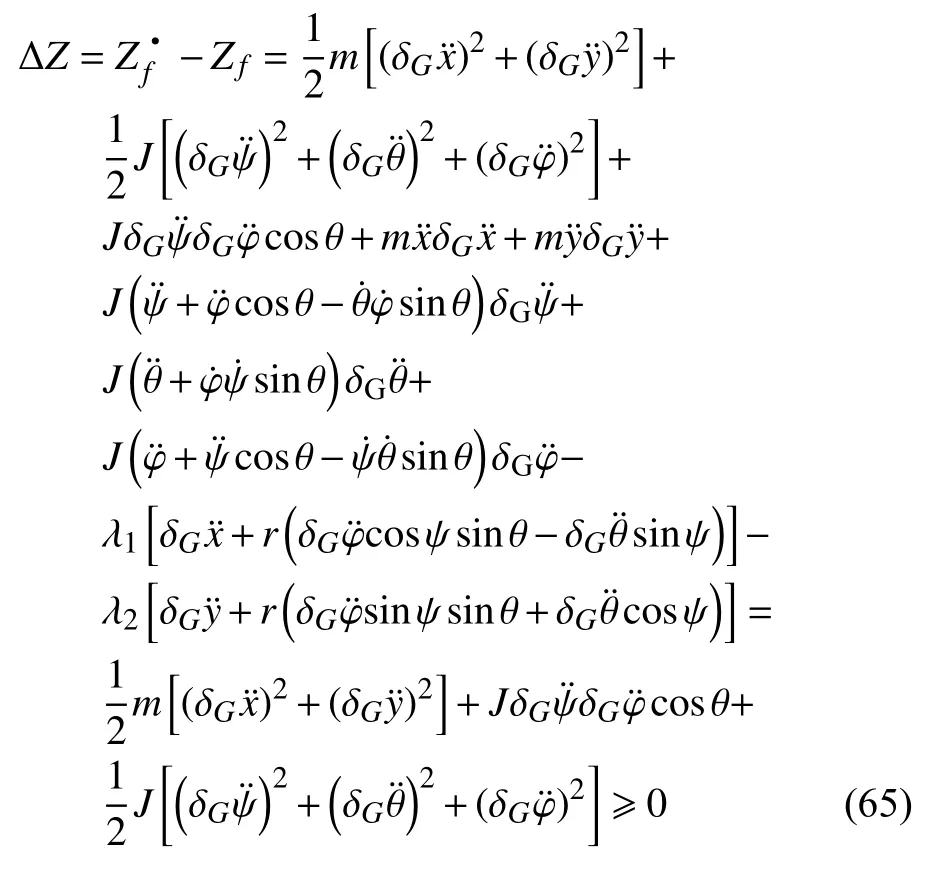
因此,真实运动的拘束函数Zf取得极小值.
例2.变质量Hamel 例[40].
质量为m=m(t) 的质点在力的作用下在空间中运动,它的运动受有理想三阶非完整约束
试建立质点的运动微分方程.
解:以x,y,z为广义坐标,质点的加速度能为
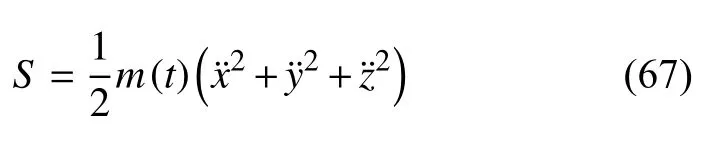
由式(11),拘束Z为

其中Q1,Q2,Q3是广义力,u1,u2,u3是质点分离或并入的微粒相对质点的速度u在三个坐标轴上的投影.
约束方程(66)可写成

因此,广义拘束函数(49)给出
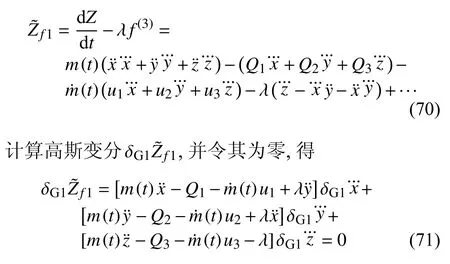
依据Lagrange 乘子法,由式(71)可得
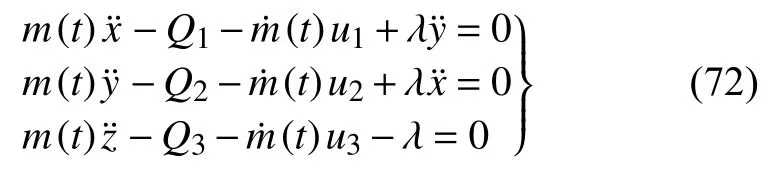
这是系统的运动微分方程.方程(72)与文献[40]用Nielsen 方程给出的结果一致.
4 结论
与d’Alembert 原理和Jourdain 原理不同,高斯原理是极值原理,由此可直接获得质点系的运动[5-7].而变质量系统在工程实际和自然界普遍存在,因此研究变质量力学系统的广义高斯原理及其最小拘束形式具有重要意义.
(1)建立了变质量力学系统的高斯最小拘束原理,构造了非完整系统修正的拘束函数,得到了变质量二阶线性和一阶非线性非完整力学系统的高斯最小拘束原理.

(2)提出了变质量力学系统任意阶情形的广义高斯原理,并通过对拘束函数求k阶导数定义k次加速度空间的广义拘束函数,建立了变质量力学系统广义高斯最小拘束原理.
(3)构建高阶非完整系统的广义拘束函数,建立了变质量高阶非完整力学系统的高斯最小拘束原理.

