可重构力学超材料的设计与波动特性研究1)

肖伯雅 杨 洮 冯亚菲 刘 宇 徐文帅 陈 猛,2) 姜 恒,3)王育人

* (中国科学院力学研究所微重力实验室,北京 100190)

† (中国科学院大学工程科学学院,北京 100049)

** (中国人民解放军92228 部队,北京 100072)

引言

力学超材料由于其超常的物理属性,如负泊松比[1-2]、剪切模量消隐[3]、负压缩性[4]、可调刚度[5-7]、轻质高强[8]等,结构往往具备良好的抗变形、耐疲劳或耐高压能力,在航空航天轻质高强结构[9-10]、隔振吸能结构[11-13]、深海耐压结构[14-15]等领域有着广泛的应用.其中具有可调刚度的可重构双稳态结构可以通过外加力场的方式主动调控整体结构的构型,这一独特属性给研究人员提供了极大的设计自由度,大大拓展了功能材料的设计空间,因此近年来双稳态结构受到科研人员的广泛关注.

弯曲梁模型作为典型的双稳态结构于2004 年由Qiu 等[16]提出,利用深反应离子刻蚀(DRIE)制备了微米级的双稳梁,进行了试验和仿真计算,其测试结果与仿真结果基本一致.起初双稳态梁结构主要应用于微机电系统(MEMS),Wu 等[17]利用双稳态梁结构设计制造出了微悬臂致动器,可以应用于低功率双稳态继电器中.Huang 等[18]通过双稳态梁结构与杠杆结构组成的双稳态装置,用来制作微机电系统中具有双稳性和推入推拉功能的设备.后续科研人员对双稳态梁结构也进行了力学方面的研究,Yang 等[19]利用热塑性聚氨酯弹性体橡胶(TPU)成功制备了弯曲梁双稳态结构,研究了结构几何参数对整体力学性能的影响.之后Darwish 等[20]将钢板作为骨架,用尼龙材料制备了弯曲梁可重构结构,研究了多成分材料结构稳态转变过程中的力学特性.Zhang 等[21]用PLA 材料作为骨架,将0.1 mm 厚的钢板加工成弯曲梁结构,两者合成的新型多稳态结构相比于之前的同类结构多了倾斜的稳态构型.Hua 等[22]研究了弯曲梁结构在隔振和吸能方面的性能,发现当拱高与曲梁厚度之比为3.6 时结构具备最优的隔振吸能性能.Chen 等[23]利用弯曲梁结构设计出了多层圆环式的多稳态结构,系统研究了几何参数对稳定状态的影响,提出了三层超材料结构实现多稳态功能的有效方法.Yang 等[24]设计制造了可编程的周期性排列一维多稳态圆柱结构,可以实现稳定且可重复使用的构型转变.

同时,带隙可主动调控的结构一直都是科研人员关注的热点,而弯曲梁双稳态模型的出现为主动调控提供了一条新途径,在此之前实现主动调控的方式普遍都是通过外加各种物理场的形式来改变特殊胞元材料的密度和模量来实现的.Chen 等[25]提出了基于压电材料以及电流变弹性体的主动弹性超材料,同时进行了理论分析和数值验证,可以用来设计目标带隙结构以及特殊的波导装置.Xia 等[26]利用声学传输线法(ATLM)研究了温度对声学超材料产生带隙的影响,结果发现温度变化对结构的色散特性具有显著影响,为主动控制声学超材料的设计提供了新的方法.Zhang 等[27]通过在环氧树脂杆上周期地布置含有负电容的压电分流单元,构造了压电声子晶体杆结构,通过理论和仿真计算证明通过改变不同谐振频率的压电分流单元的个数,获得多个局域共振带隙,增强带隙可调谐性.在弯曲梁双稳态结构提出之后,大量的研究集中在构型转变对结构色散特性的影响上.Meaud 等[28]研究了弯曲梁双稳态结构不同构型下的色散关系,仿真结果表明两种构型下结构的色散特性发生了改变,该结构可以应用于声学开关.Tan 等[29]提出了一种基于屈曲的可编程负刚度超材料,通过横向约束实现了结构构型的转变,结果表明稳态转换可以调控弹性波的传播,并指出在主动调控声学超材料方面引入形状记忆材料值得尝试.Liu 等[30]研究了周期性双稳态结构的非线性弹性响应,特别是冲击波响应方面,结果表明结构一定程度上可以衰减冲击波的强度,可以用于精密设备的保护.Hu 等[31]利用形状记忆材料(SMP)制备了弯曲梁双稳态结构,结构无需外加物理场的激发就可以实现构型的自主转变,同时系统地研究了模型的色散关系.针对不同构型的弯曲梁双稳态结构色散特性研究基本都局限于二维的平面构型之中,而二维的可重构结构在外力驱动调控之下由于其端部缺乏约束以及平面厚度较窄等因素,结构往往会发生横向变形和面内弯曲,导致达不到稳态转变的变形要求.Hua 等[32]设计出了圆柱式的空间多稳态结构,探讨了多稳态结构作为吸能结构的应用前景并研究了几何参数对结构吸能性能的影响.Giri 等[33]也对圆柱式多稳态结构进行了研究,主要分析了多层可重构结构中单层几何参数的设置对整体构型转变顺序的影响,同时也对其吸能性能进行了对比.圆柱式空间可重构结构的提出解决了以往二维平面可重构结构容易产生多余变形的问题,周期性排列的平面可重构结构可以相互为对方提供端部约束.但是针对三维空间构型的可重构结构的研究集中在其力学性能方面,特别是结构的吸能性能,而对其色散特性的研究工作进行得很少.

因此,本文设计了基于弯曲梁结构的六角空间可重构模型,研究其构型转变过程中的力学特性以及不同构型形式下的色散特性.第一节构建中心受压直梁模型,从理论出发探明可重构结构构型转变的基理,并设计了六角的空间可重构结构;第二节介绍了标准拉伸试验以及结构力学性能及声学性能方面的仿真计算,并进行了相应的讨论分析;第三节总结本文的研究成果.本工作采用数值仿真方法,研究了六角空间双稳态结构的力学特性与色散特性,以期为后续的进一步研究提供参考数据.

1 理论分析及结构设计

1.1 双稳态机制研究

基于弯曲梁可重构机制进行理论分析,建立中心受压、两端固定的弯曲梁模型,探明稳态转变的内在机理,弯曲梁模型如图1 所示.

图1 双稳态屈曲梁模型Fig.1 Bistable buckling beam model

梁的基本微分方程为

式中,E为材料的杨氏模量,I=bt3/12 为梁的横截面惯性矩,w为梁的挠度,p为梁的轴向力.其满足的几何条件为

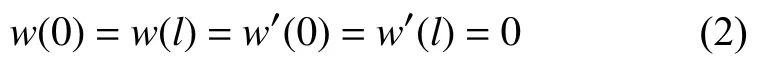
其通解为

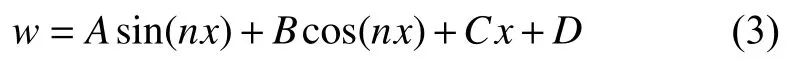
最终求得挠曲线方程的两类解.第一类为

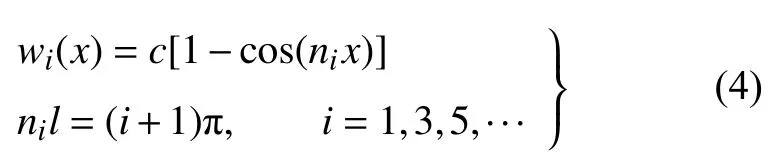
第二类为

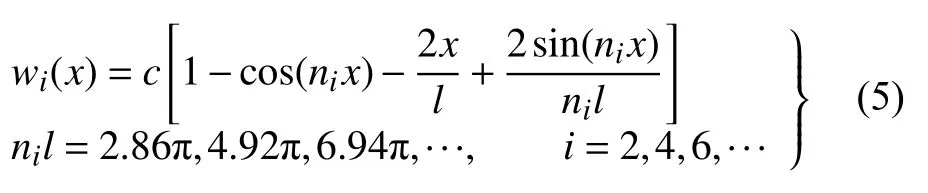
式中c为待定常数.

曲梁的初始形状为

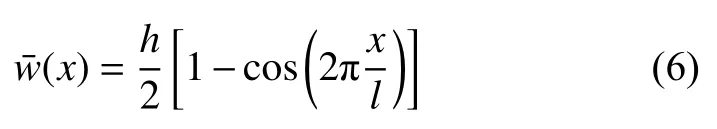
变形过程中轴向变形为dp,则变形过程中曲梁的真实长度为

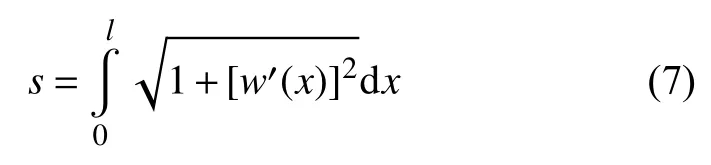
曲梁在受到力f作用变形时,挠曲线可表示为式(4)和式(5)中解的叠加,即

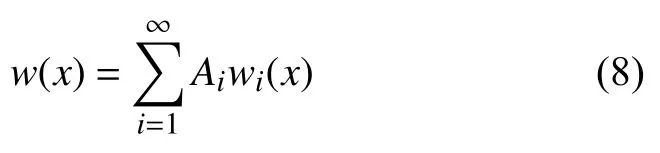
式中,Ai为叠加各项的系数,曲梁中点的位移d可表示为

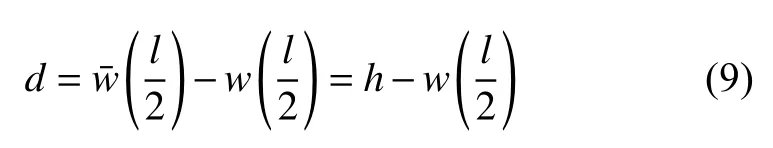
根据胡克定律,轴向力为

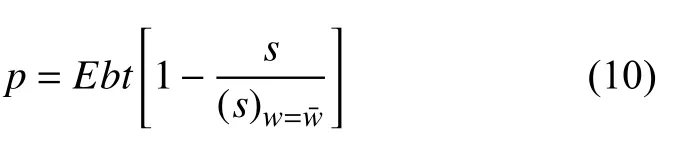
曲梁的轴向变形为dp,在变形过程中由于轴向力压缩产生的压缩应变能为

由于弯曲产生的应变能为

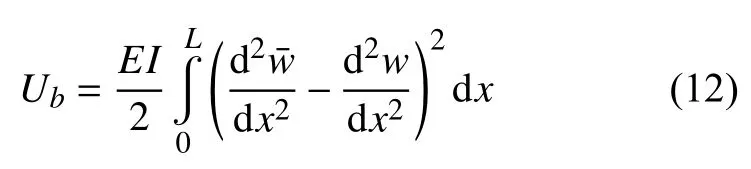
由外力f做功引起的势能变化为

系统的总能量表达式为

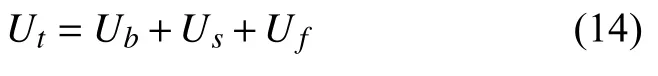
令 ∂Ut=0 ,由 ∂(Ai)|i=1,5,9,···=0解得各项的系数Ai

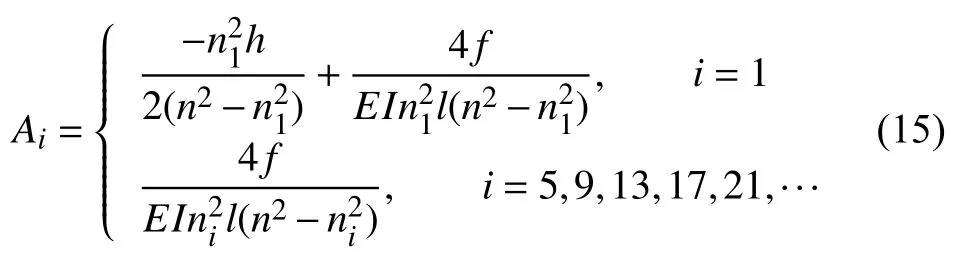
当i=2,3,4,6,7,··· 时,有

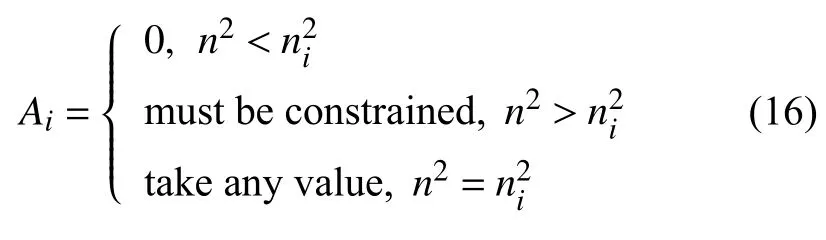
在变形过程中轴向力只能连续变化,因此第一种形式的力-位移关系是

由于梁的变形主要取决于前三阶屈曲模态,联立式(9)、式(15)和式(17)并忽略高阶模态(即Ai取0),解得

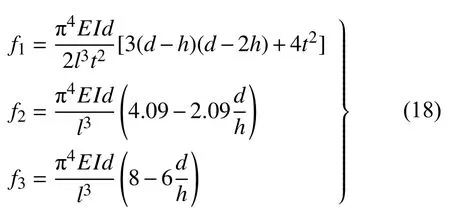
定义拱高厚度比Q=h/t,当Q取值不同时,力-位移曲线也会发生相应变化,如图2 所示.

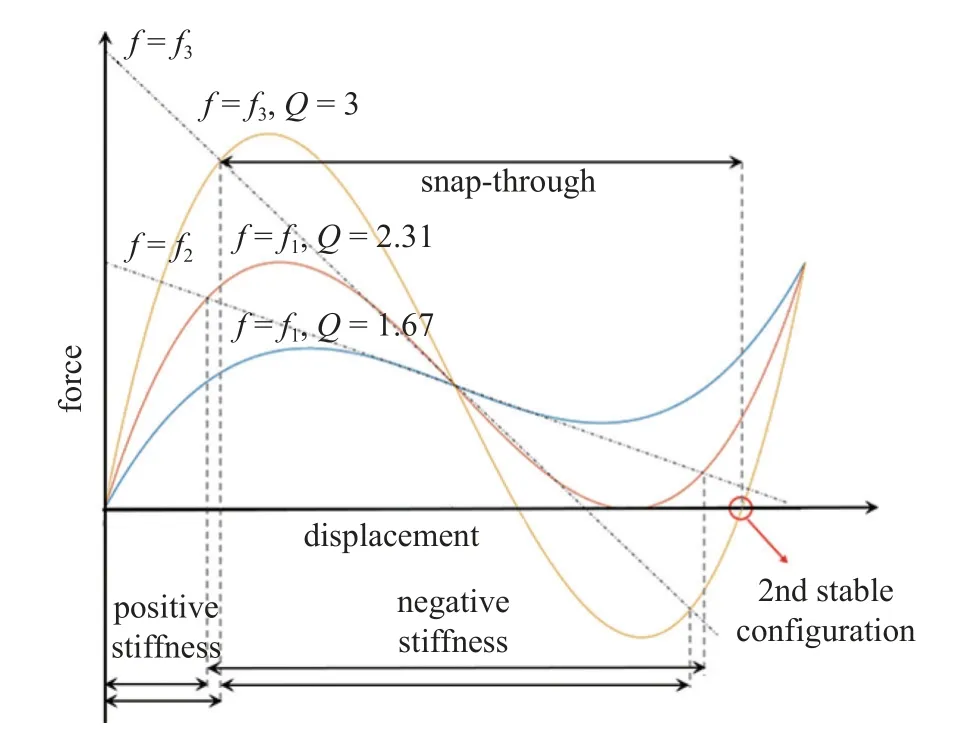
图2 弯曲梁的不同力-位移特性Fig.2 Different force-displacement behaviors

由力-位移曲线图可以看出,当Q达到第二阶屈曲变形的临界值2.31 时,力-位移曲线此时正好与x轴相切,Q大于2.31 的情况下,梁的变形情况由第三阶屈曲模态决定,比如Q=3 时,变形过程力出现负值,表明结构此时已经具备了双稳态特性.在发生由第二阶屈曲模态和第三阶屈曲模态所决定的变形过程中结构具备明显的正刚度阶段以及负刚度阶段,特别是在Q=3 的情况下,其负刚度阶段即为结构发生突弹跳变(snap-through)的过程,在图2 中红圈标注处,当结构力值再次为0 时,此时结构的势能达到另一个极低点,意味着结构此时转变为另一个稳定的构型.

1.2 六角型模式转换结构设计

外力作用下单个二维的可重构结构在变形的过程中往往会发生面内弯曲,而且最大承载力也比较小,这些问题限制了模式转换功能性材料的应用范围.因此,为了保证整体结构变形的稳定性,提高结构的承载峰值力,基于二维的可重构结构单胞设计了六角型的模式转换结构,结构的具体几何参数如图3(a)所示,曲梁的跨长为l,拱高为h,自身厚度为t,上下框架结构的宽度均为a,结构整体厚度为b,通过SolidWorks 得到的整体架构如图3(b)所示.

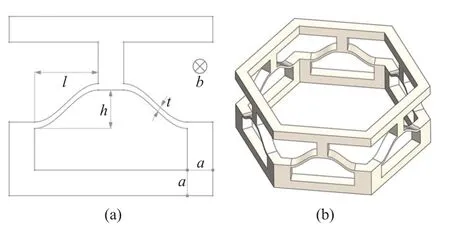
图3 六角型结构示意图Fig.3 Hexagonal structure

2 标准拉伸试验与数值仿真

2.1 标准拉伸试验

选用万华化学公司热塑性聚氨酯弹性体橡胶(TPU)作为制备双稳态结构的打印材料.TPU 材料的弹性模量可以通过单轴拉伸实验测得,参考GB/T 528—2009 设计了单轴拉伸试件,试件的几何尺寸如图4 所示.

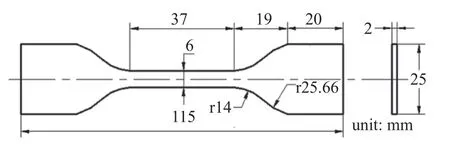
图4 基于GB/T 528—2009 的拉伸试样的尺寸Fig.4 Dimensions of tensile specimen based on GB/T 528—2009

为获得材料的力学参数进行了标准拉伸试验,拉伸的速度设为20 mm/min,采用引伸计记录单轴拉伸过程中标定段的位移,最终测得试样的平均弹性模量为145.2 MPa,泊松比为0.46.图5 为测试照片.

图5 标准拉伸测试Fig.5 Standard tensile test

2.2 结构力学性能数值仿真分析

通过双稳态机制的理论分析得知: 弯曲梁单胞的几何参数(弯曲梁的厚度t、拱高h)对结构的力学性能起着决定性作用,为探明六角型结构几何参数对其整体力学性能的影响,采用控制变量方法,设定t=1 mm,b=4 mm,l=10 mm,h从2 mm 到9 mm,步长为1;a为1 mm 到5 mm,步长为0.5.利用ABAQUS/Explicit 研究不同几何参数下结构变形过程中的力学行为.仿真过程中通过在模型上表面耦合点施加位移载荷的方式实现整体结构的变形,同时在模型底部施加固定约束(如图6 所示).依照标准拉伸测试测得数据,采用 neo-Hookean 超弹性模型对材料本构进行拟合,网格划分选用8 节点线性减缩积分实体单元(C3D8R).

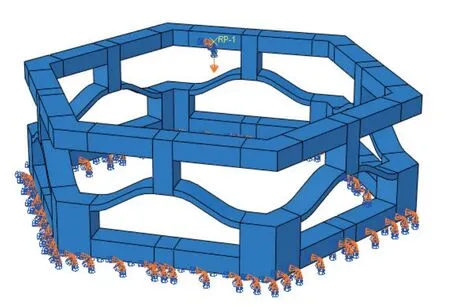
图6 ABAQUS 仿真示意图Fig.6 ABAQUS simulation schematic diagram

对不同几何参数六角型结构进行系统化的仿真分析,得到了两者之间对应关系的相图(图7).

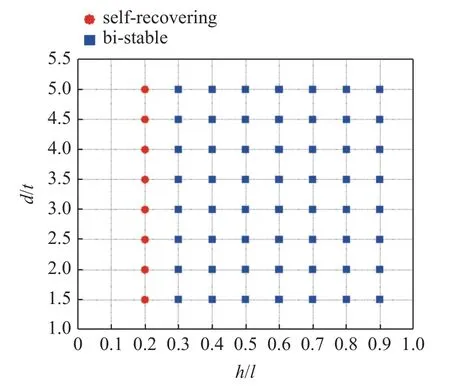
图7 几何参数与力学性能相图Fig.7 Phase diagram of geometric parameters and mechanical properties

结果显示当曲梁自身宽度t固定为1 mm,跨长l固定为10 mm,其拱高h与曲梁跨度l比值比较小如0.2 时,随着下压位移的增加结构呈现出负刚度特性,但作用力始终为正值,说明结构此时具备自恢复特性;而当两者比值达到0.3 后,随着下压位移的增加结构也呈现出负刚度特性,不同的是作用力出现了负值的情况,说明结构具备双稳态特性.通过几何参数与力学性能之间关系的研究分析,可以根据目标性能设计出构型合理的可重构超材料结构.

2.3 结构色散关系数值仿真分析

通过上述力学性能数值仿真分析得知具备双稳态特性的结构可以实现可控变形的能力,图8 展示了六角型空间结构的构型转变行为,而其构型的改变会导致色散特性出现变化,为了研究构型改变对色散特性的具体影响情况,利用有限元数值仿真对双稳态结构进行了色散关系分析,在上下表面施加floquet 周期性边界条件,对结构竖直方向(z方向)色散特性进行数值计算,得到不同构型下结构的色散曲线.图9 和图10 分别给出了a=2 mm,h=4 mm 情况下拉伸和压缩两种构型下的色散关系曲线.

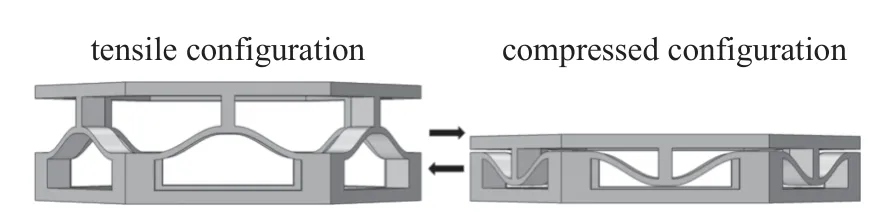
图8 几何构型转变Fig.8 The geometric configuration switching

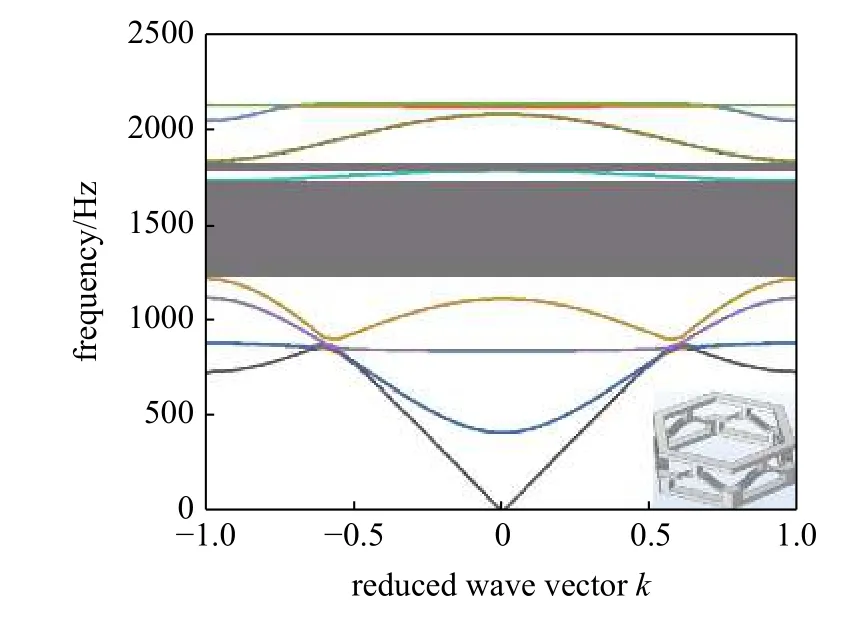
图9 拉伸构型下的色散关系曲线Fig.9 Dispersion relationship curve in stretched configuration

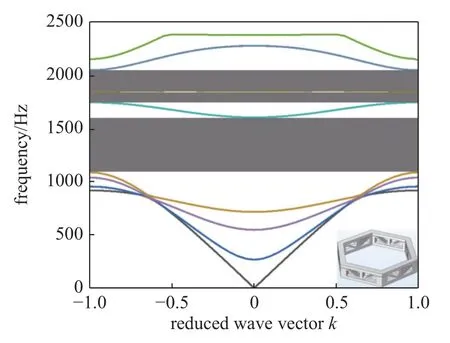
图10 压缩构型下的色散关系曲线Fig.10 Dispersion relationship curve in compressed configuration

结果显示在拉伸构型下结构在计算频率范围内形成了两个完全带隙,分别位于1224.29～1740.16 Hz,1794.16～1842.44 Hz.其中第一带隙位于第六支与第七支色散曲线之间,第二带隙位于第七支与第八支色散曲线之间.而压缩构型下在计算频率范围内则产生了三个带隙,分别位于1087.22～1603.46 Hz,1745.19～1846.91 Hz 和1850.53～2047.68 Hz.其中第一带隙介于第六支与第七支色散曲线之间,第二带隙介于第七支与第八支色散曲线之间,第三带隙介于第九支与第十支色散曲线之间.可以看出结构构型从拉伸转变为压缩的过程中,结构的第一带隙向低频方向移动,压缩构型下的第二带隙相比于拉伸情况下禁带频率范围有所增加,另外由于构型的转变导致结构的晶格常数发生了变化,从而改变了其色散模式,在压缩构型的情况下产生了新的第三带隙.

仿真结果初步说明可以通过结构构型的调整来改变结构的波动特性,实现对波的主动控制.此外拉伸构型下两个带隙中心频率对应的波长分别为0.282 m,0.198 m.而拉伸构型下晶格尺寸为0.018 m,说明结构可以在亚波长尺度下形成带隙,可以推断出这些带隙是由局域共振机制引起的.为了进一步验证六角型双稳态结构的带隙形成机制,对其截至频率处的振动模态进行了研究分析,如图11 所示,从左至右依次给出了拉伸构型下两个带隙截至频率处的振动模态图,可以看出在第一带隙的振动模态主要表现为上下质量块的振动,而在第二带隙的振动模态图中可以看到框架结构保持静止而单胞的中间连接部分在振动,结合之前对中心频率处波长的计算数据可以判定拉伸构型下的第一带隙是由于上下框架结构作为质量块振动引起的局域共振,而第二带隙则是由于弯曲梁部分振动引起的局域共振.同时构建了两种构型的动力学特性分析模型以进行频率响应(frequency response)计算,如图12 所示两者的动力学特性分析模型均为单胞沿z轴周期性排布形成的,阵列数量为10.将模型中底部单胞下表面的边界定义为激励位置,施加沿z轴正向的指定加速度,加速度数值为0.1 mm/s2,并在此边界定义积分条件作为频响计算的初始值.同样将模型端部第一个单胞的下表面作为响应位置,定义积分条件作为频响计算的响应值.

图11 模态振型Fig.11 Modal diagram

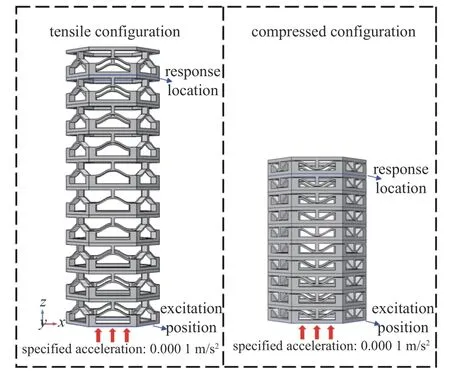
图12 色散特性分析模型Fig.12 Dispersion characteristic analysis model

得到的结果如图13 所示,频响计算更为直观地展现了结构构型改变对自身色散特性带来的变化,从拉伸构型到压缩构型的转变过程中,带隙是朝着低频方向移动的.

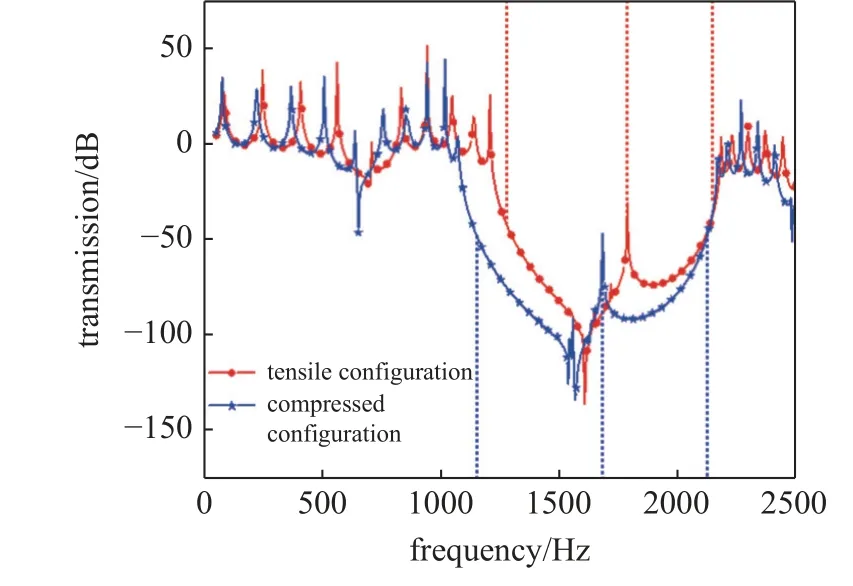
图13 频响曲线Fig.13 Frequency response curve

另外,对其他不同几何参数的结构也进行了相应的带隙计算分析,通过柱状图的形式展示了带隙随着几何参数的变化情况,如图14～图17 所示.

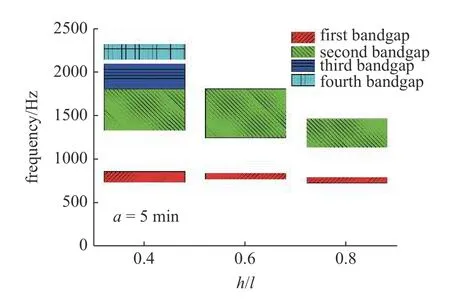
图14 拉伸构型下带隙变化柱状图Fig.14 Histogram of band gap change in tensile configuration

图14 为t=1 mm,a=5 mm,l=10 mm 情况下,结构在拉伸构型下产生的带隙随着拱高h的变化示意图,在h=4 mm 即h/l=0.4 时结构产生了四个带隙,分别位于744.86～867.38 Hz,1336.86～1815.21 Hz,1820.92～2106.35 Hz 以及2148.52～2325.64 Hz 处;当h为6 mm 即h/l=0.6 时,结构仅产生了两个带隙,分别位于777.95～852.12 Hz,1255.36～1814.53 Hz处;当h为8 mm 即h/l为0.8 时,结构产生了两个带隙,位于735.93～803.74 Hz,1145.05～1468.66 Hz 处.可以看出在拉伸构型下,随着拱高h的增加,结构的带隙总体是朝着低频移动的,而且h为4 mm 时结构在1800 Hz 之上产生的两个带隙随着h的增加消失了.图15 为t=1 mm,a=5 mm,l=10 mm 情况下,结构在压缩构型下产生的带隙随着拱高h的变化示意图,可以看出随着拱高h的增加,带隙数量逐渐减少,当h为8 mm 时结构仅产生了一个带隙.

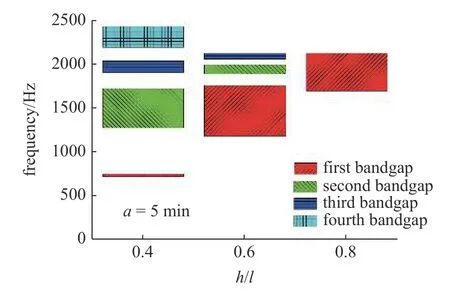
图15 压缩构型下带隙变化柱状图Fig.15 Histogram of band gap change in compressed configuration

图16 给出了t=1 mm,h=6 mm,l=10 mm 的情况下,结构在拉伸构型下产生的带隙随着框架宽度a的变化示意图.当a为2 mm 即a/t=2 时结构产生了一个带隙,位于1254.93～1665.67 Hz 处;当a为3 mm 即a/t=3 时结构也产生了一个带隙,位于1216.04～1772.81 Hz 处;当a为4 mm 即a/t=4 时结构产生的带隙位于1270.88～1836.05 Hz 处;当a为5 mm 即a/t=5 时结构产生了两个带隙,其中第一带隙位于777.95～852.12 Hz,第二带隙位于1255.36～1814.53 Hz 处.总体来看框架宽度对结构的带隙的影响作用甚微,除了在a=5 mm 的情况下产生了一个新带隙之外,其他情况下带隙的位置和带宽变换均不大.图17 给出了t=1 mm,h=6 mm,l=10 mm 的情况下,结构在压缩构型下产生的带隙随着框架宽度a的变化示意图.可以看出与拉伸构型相同,框架宽度a对结构带隙的影响不大,随着a的持续增加,带隙总体是朝着高频移动的,但移动幅度也很有限.

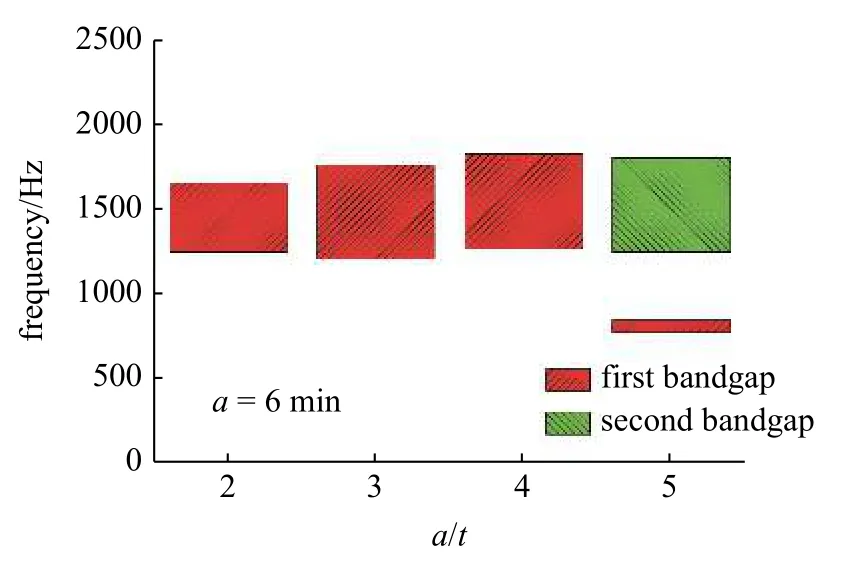
图16 拉伸构型下带隙变化柱状图Fig.16 Histogram of band gap change in tensile configuration

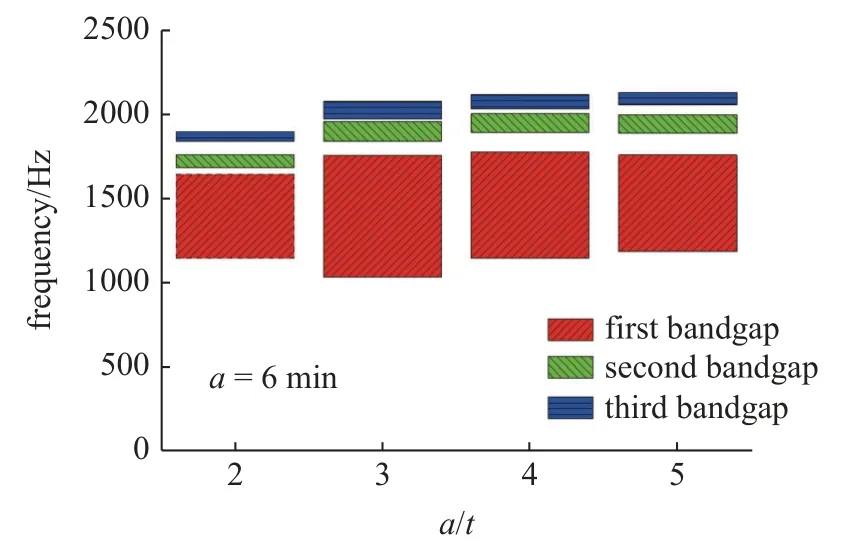
图17 压缩构型下带隙变化柱状图Fig.17 Histogram of band gap change in compressed configuration

结构构型转换及几何参数的变化对色散关系产生的影响证明,可以通过改变具备双稳态特性结构的构型来主动调控波的传输特性,另一方面也可以根据目的带隙来逆向设计合理几何参数的双稳态结构.

3 结论

本文基于弯曲梁双稳态结构设计了六角型可重构结构,并利用有限元数值仿真进行了力学性能与色散特性分析.首先研究了六角型可重构结构几何参数对其整体力学性能的影响,得到了具备自恢复、双稳态特性的具体结构几何参数;之后在具备双稳态特性结构的基础上进行了两种构型下的色散关系分析,研究构型变化对结构色散关系的影响并进行了相应的频率响应计算.得到的结论可以总结如下.

(1) 通过研究几何参数对结构力学性能的影响,得到了具备不同力学性能的结构几何参数,在弯曲梁自身宽度t为1 mm 且跨度l为10 mm 的基础上,当h/l大于等于0.3 时即h取值大于等于3 mm 时结构即呈现双稳态特性,而h取值为2 mm 时结构则呈现自恢复特性.

(2) 具备双稳态特性的结构在两种构型下的色散曲线发生明显变化,在t=1 mm,a=2 mm,h=4 mm,l=10 mm 的情况下,其压缩构型下的带隙相比于拉伸构型下,具备明显的朝向低频移动趋势.两种构型几何特征的改变导致其晶格常数出现差异,进而影响到结构整体的色散特性,导致带隙的位置、范围以及数量均发生变化.

(3) 通过对六角型可重构结构力学性能和色散特性的分析,初步证明可以通过调整结构的几何参数实现对整体力学性能的主动设计和色散特性的主动调控,可以根据应用需求设计合适的结构构型.