高阶色散下双耦合微腔中克尔光频梳的稳定性和非线性动力学分析*

许凡 赵妍 吴宇航 王文驰 金雪莹

(合肥工业大学仪器科学与光电工程学院,测量理论与精密仪器安徽省重点实验室,合肥 230009)

在考虑光学微腔中高阶色散效应的情况下,以耦合非线性薛定谔方程为理论模型,研究了高阶色散作用下双耦合微腔内克尔光频梳的稳定性和非线性动力学,并讨论了各阶色散参数对腔内光场演化和光谱特性的影响.理论分析结果表明,三阶色散的加入使得参量空间的稳定域扩大,周期性变化的呼吸孤子态和混沌态转变为稳定的亮孤子态.此外,各高阶色散项及其组合对光频梳的光谱特性包括最大失谐、腔内脉冲峰值功率、色散波频谱位置等有显著影响.具体地,三阶色散和正四阶色散能够展宽光谱,增强色散波;而负四阶色散抑制色散波产生,得到对称的孤子频率梳;五阶色散可以调控光孤子的漂移方向和速度.理论研究结果对于双耦合微腔实验中的色散调控及设计、稳定性研究具有重要价值.

1 引言

基于光学微腔的克尔光频梳凭借其跨倍频程宽光谱、高重复频率、低功耗和高集成度等优点,在光钟[1]、高速通信[2]、超快距离测量[3]、双光梳光谱[4]等领域具有广泛的应用价值.回音壁模式光学微腔因其具有超高品质因子(Q值)和极小模式体积,使得腔内具有极高的能量密度,从而能够在低阈值下激发级联四波混频效应,将泵浦光场转移到邻近的模式中,形成一系列宽带的梳状光谱[5].目前,国内外很多研究小组开展了关于微腔光频梳的研究,已经对腔内不同状态的光场进行了理论和实验上的验证,如孤子态、图灵环态、呼吸孤子态和混沌态等[6-8].其中,时域孤子的稳定产生取决于克尔非线性与色散、增益与损耗之间的双平衡[9].具体来说,克尔非线性效应不仅使腔内产生了新的频率分量,还会使光场出现啁啾,而脉冲宽度保持不变.微腔内色散的存在会使得脉冲出现时域展宽现象,但不会产生新的频率分量.当色散和克尔非线性效应造成的时域啁啾相互抵消时,形成了一个平衡,这使脉冲形状不会随时间发生改变.参量增益为泵浦的激励能量,而损耗包含腔内线性损耗、能量耦合损耗等各种形式损耗.在增益和损耗作用下,腔内能量随着演化时间更迭最终达到平稳状态,这形成了又一个平衡,其决定了腔内峰值功率.当克尔微腔中同时满足以上两个平衡条件时,腔内会形成耗散稳态单孤子.单孤子态对应的高相干度的平滑包络光频梳,对于精密光谱、低相位噪声微波产生具有重要意义.此外,研究发现,双耦合微腔中可以产生耗散性孤子,并表现出单腔所不具有的非线性现象[10],如超模孤子的产生和孤子跳跃.其中,对于超模孤子而言,在对称超级模和反对称超级模中光孤子的形成差异较大.并且在耦合微腔系统中,横模耦合导致的模式反交叠得到明显抑制[11].在跨倍频程克尔光频梳的研究中,当二阶色散接近于微腔器件零色散点附近时,高阶色散将对光场演化起到主导作用,其影响不能被忽略.高阶色散的存在影响腔内光孤子演化和光谱特性,一般可通过调控微腔几何形状 (如调控微环腔横截面的长宽比) 从而控制高阶色散的大小.Kippenberg 等[9]发现调控微腔色散能够调节调制不稳定态的增益,从而优化光频梳光谱.Brasch 等[12]通过在近零色散点泵浦可以产生高效的切伦科夫辐射,进而展宽光频梳光谱.Parra-Rivas 等[13]利用三阶色散稳定克尔光频梳.Okawachi 等[14]研究了四阶色散对于光频梳光谱带宽的影响.Cherenkov 等[15]研究了孤子与色散波之间的相互作用,证明了色散波的形成会导致孤子光谱包络的移动,其产生有利于将光频梳的扩大至正色散区.

针对微腔内光孤子产生过程中能量转化效率低的问题,Xue 等[16]提出了一种新型的双耦合微腔结构,通过双微腔耦合的方式,能够打破传统单个微腔的转化效率极限,实现近100%的泵浦-光孤子的能量转换效率.此外,双耦合微腔与单个微腔相比具有更多的可调参数和稳定的光场[17].目前,关于双耦合光学微腔的研究工作还比较局限.已有学者研究了微腔中的混沌现象[18],讨论了双耦合微腔内的光谱特性以及可调谐参数的影响[19],但是对于双耦合微腔内的研究,没有考虑到高阶色散的影响.关于三阶色散以及更高阶色散对于耦合微腔内克尔光频梳工作状态的激发和稳定性的影响,缺乏相关详细研究.

本文以双耦合微腔结构内的耦合非线性薛定谔方程为理论模型,详细研究了在耦合微腔中不同阶高阶色散及其组合对于克尔光频梳的稳定性、光场演化以及光谱特性的影响.理论研究表明,三阶色散项使得参量空间的稳定域扩大,能够抑制克尔光频梳的不稳定态,如呼吸孤子、混沌态,形成稳定的单孤子态.讨论了高阶色散的稳定机制.高阶色散会影响克尔光频梳的光谱特性和光谱包络形态,三阶色散和正四阶色散项可以激发并增强色散波,而负四阶色散项会抑制色散波的产生.有趣的是,五阶色散项可调控光孤子的漂移方向及速度.因此,为得到精确的克尔光频梳包络,应该考虑高阶色散的影响.最后,研究了泵浦功率对于色散波辐射频率的影响.

2 理论模型与计算方法

本文所研究的回音壁模式双微腔耦合系统如图1 所示,该结构包含两个耦合的微腔,其中一个微腔能够支持克尔孤子,称为孤子腔;另一个微腔用于传递泵浦光能量至孤子腔,称为泵浦腔.泵浦光经波导耦合到泵浦腔中,两个微腔之间通过倏逝场耦合,耦合强度通过两微腔的耦合间距控制,最终光场从孤子腔的下路耦合端口(D)输出[19].孤子腔和泵浦腔中的光场分别用E1和E2表示,则两个微腔中的光场可以用耦合非线性薛定谔方程[16]来描述,其中包含高阶色散项:

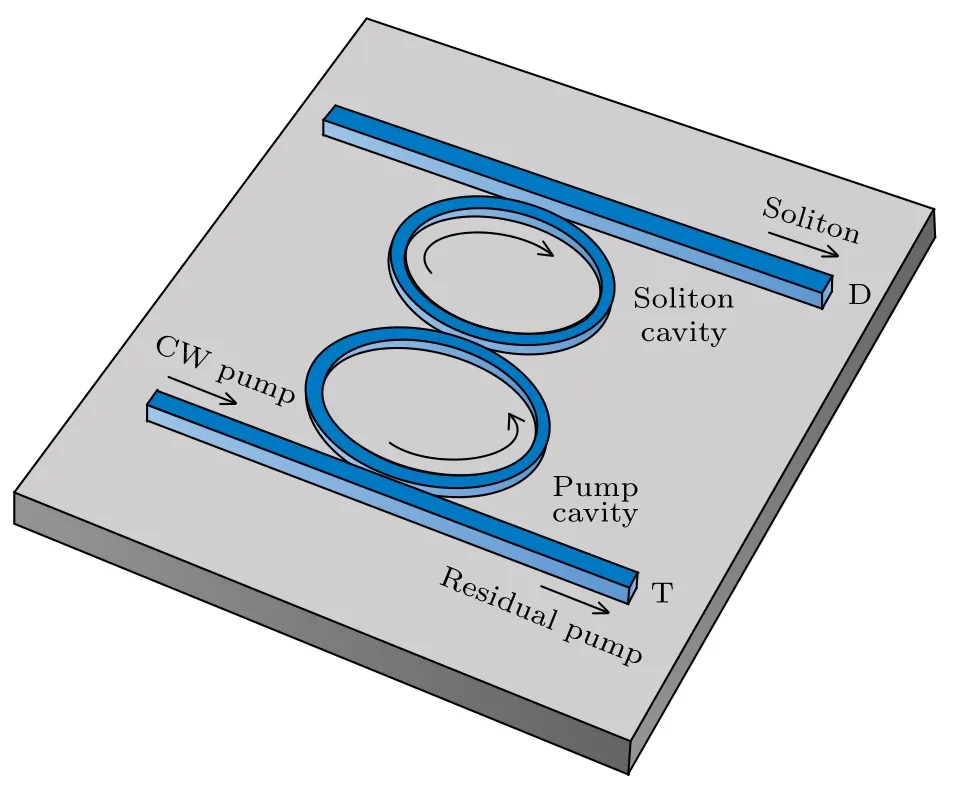
图1 双耦合光学微腔结构Fig.1.Structure of dual-coupled optical microcavities.

透射端口(T)和下路耦合端口(D)的输出光场可以表示为

这里,z表示光在微腔中传播的距离;τ是光场传播的快时间,对应于微腔的角位置;αi1和αi2是微腔内单位长度的本征损耗;αc1和αc2是微腔内单位长度的耦合损耗,αc1=θ1/(2L),αc2=θ2/(2L),其中θ1和θ2分别代表两个微腔与输出波导和输入波导之间的耦合系数;δ1和δ2为两个微腔的谐振频率和泵浦频率之间的失谐;kp,kd分别为孤子腔和泵浦腔单位长度的耦合效率,κp=,κd=;L是孤子腔的腔长;Δk′为群速度失配;k1m和k2m分别表示微腔1 和微腔2 的m阶色散系数;γ1和γ2为非线性系数,与微腔的材料有关;κ12=κ21=,θ12=θ21为两个微腔之间的耦合系数;Pin为泵浦光的功率,Ein=.光在微腔内循环一周的时间用tR表示,微腔的自由光谱范围 (FSR) 定义为νFSR=1/tR,表示微腔光频梳梳齿之间的间隔.采用相对色散系数d13,d14,d15分别表示孤子腔的三阶、四阶、五阶色散,其表达式为[20]

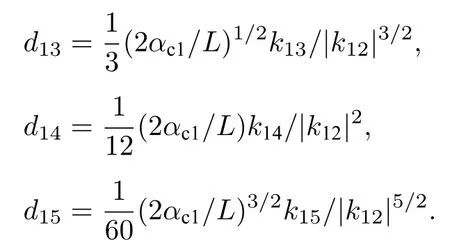
采用分步傅里叶算法[21]求解耦合非线性薛定谔方程(1)和(2),模型计算时间长度为tR1=5 ps,tR1表示光在孤子腔内循环一周的时间,通过选择取样点数为27,单步传输时间为tR1/128,得到两个微腔内光场分布和光谱随时间的演化,在接近60000tR后光场会呈稳定状态.结合(3)式和(4)式可以得到耦合微环腔D 端口的输出光场以及T 端口的透射谱.具体地,求解时将方程分解为线性项、非线性项和泵浦项,将泵浦项合并入线性项,在频域求解;在时域求解非线性项.

3 理论结果与分析

3.1 各阶色散对孤子的稳定性分析

以Si 为基底的Si3N4双耦合微腔的各项参数设为:γ1=γ2=1 m—1·W—1,δ2=8.089 m—1,Δk′=1.282×10—10s·m—1,θ1=9.114×10—3,θ2=1.063×10—2,θ12=θ21=3.038×10—3,k12=—100 ps2/km,k22=100 ps2/km,L=1.499 mm.此外,耦合的两个微腔的FSR 分别为:νFSR1=200 GHz,νFSR2=192.6 GHz;失谐参量δ1,2=2π·Δf1,2/(νFSR1,2L),其中Δf1,2为泵浦与两个微腔谐振频率之间的频率失谐量,可以通过调节泵浦光频率或调节光学微腔谐振频率来调控Δf1,2,后者可以采用热调谐[22]或机械调谐方法[23]实现.孤子腔(腔1)设为反常色散,能够支持孤子态光场;而泵浦腔(腔2)设为正常色散从而抑制调制不稳定性,为孤子腔提供能量支持.腔内初始光场由调制不稳定性产生,因此可设定其符合高斯分布.由(4)式可知,双耦合微腔结构中克尔孤子在孤子腔内产生和输出,而泵浦腔仅用于提供孤子腔的泵浦能量,因此本文重点讨论孤子腔内的光场分布和光谱特性.

首先研究三阶色散对光场的稳定作用.图2(a)和图3(a)分别展示了仅考虑二阶色散(d13=0)时,D 端口输出光场呈现的呼吸孤子和混沌状态的时域演化图,对应的光谱图如图2(c)和图3(c)所示.两种状态仅泵浦功率和失谐参数不同,仿真参数具体为: 呼吸孤子δ1=95 m—1,Pin=14 W,k12=—100 ps2/km;混沌状态δ1=110 m—1,Pin=160 W,k12=—100 ps2/km.从图2(a)可看出,仅包含二阶色散时,光场呈现随时间周期性振荡的呼吸孤子状态;当三阶色散足够大(d13=—0.0537)时,呼吸孤子状态转变为稳定的孤子态 (图2(b)).类似地,如图3(a)和图3(b)所示,当仅包含二阶色散时,输出光场呈混沌状态;当三阶色散相对系数d13=—0.0537 时,光场由混沌状态转变为稳定孤子态.这表明,当三阶色散足够大时,微腔的动态不稳定性得到完全抑制,使得输出光场由不稳定的时域振荡态或混沌态转变为稳定的孤子态.由图2(d)和图3(d)可以看出,尽管孤子的位置存在等速的时域漂移,但其梳状光谱始终保持稳定.三阶色散的加入破坏了腔内的反射对称性(τ→-τ),从而导致光场在时域和光谱上的不对称性,而这种不对称性是产生孤子时域漂移的原因[13,24].此外还可以看出,孤子频梳的载波包络中心相对于泵浦频率产生了一定的偏移,这是由色散波产生的光谱反冲导致的[25,26].

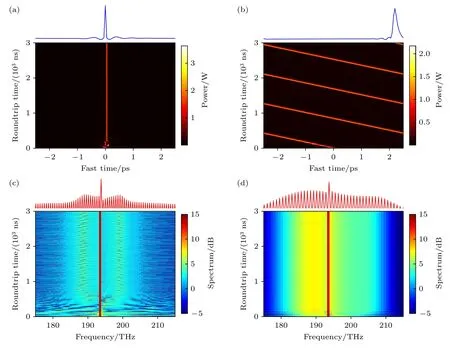
图2 三阶色散对孤子腔内周期振荡的呼吸孤子态的影响 (a),(c) 仅包含二阶色散时呼吸孤子态的(a)时域演化图和(c)光谱演化图;(b),(d) 当加入三阶色散后,腔内呈现的稳定单孤子态的(b)时域演化图和(d)光谱演化图.子图顶部为t=3000 ns 时对应的时域光场/光谱分布Fig.2.Effect of third-order dispersion on periodically oscillating breathing soliton states in a soliton cavity: (a),(c) Without thirdorder dispersion,the evolution of the temporal intensity profile (a) of breathers states and the corresponding comb spectrum (c);(b),(d) with third-order dispersion,the evolution of the temporal intensity profile (b) of soliton state and the corresponding comb spectrum (d).Temporal profile/comb spectrum at t=3000 ns are shown on the top of each panel.

为了验证三阶色散对腔内光场稳定作用的普适性,分析了针对不同三阶色散值腔内光场在整个参量空间(δ1,Pin)中的稳定性,结果如图4 所示.(1)式齐次稳态解定义为E1h(homogeneous steady state,HSS),P1h=|E1h|2,由(5)式计算得到:

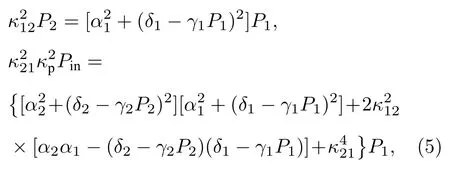
其中,P1=|E1|2,P2=|E2|2,α1=αi1+αc1,α2=αi2+αc2.当失谐量δ1＞时,腔内光场呈现双稳态,稳态解存在域可由(5)式推出[16],如图4中绿色虚线区域所示,可以看出HSS 存在域与三阶色散相对系数(d13)无关.在稳态解存在域HSS中会出现稳定孤子域、时域振荡域和混沌域这3 种状态[27],在图4 中用蓝色实线表示,整个孤子存在域随三阶色散值的增加呈缩小趋势,蓝色实线外为连续波(continuous wave,CW)状态.区域I 对应稳定的孤子态;区域II 对应随时间周期振荡变化的呼吸孤子态;增加失谐,腔内孤子时间演化导致混沌态的产生,即为区域III.图4 展示了三阶色散大小与3 种孤子存在状态及其稳定性的关系,其中k12=—80 ps2/km.当不考虑三阶色散项的情况下,这3 种状态在参量空间的分布较为均匀;随着三阶色散的增加,混沌域III 不断缩小且向失谐更大处移动,呼吸孤子域II 也逐渐缩小,并向功率更大处移动,而稳定孤子域I 不断扩大.当三阶色散系数增大至d13=—0.0938 时,时域振荡域和孤子域只有在δ1＞16 GHz,Pin＞4.5 W 很小的参量空间范围内才存在.这证实了图2 和图3 中三阶色散对于腔内孤子和梳状光谱的稳定作用在整个参量空间(δ1,Pin)中是有效的.

图3 三阶色散对混沌态的影响 (a),(c) 仅包含二阶色散时,腔内呈现振荡的呼吸孤子态(a)的时域演化和(c)光谱演化图;(b),(d) 当加入三阶色散后,腔内呈现的稳定单孤子态的(b)时域演化图和(d)光谱演化图.子图顶部为t=3000 ns 时对应的时域光场/光谱分布Fig.3.Effect of third-order dispersion on chaos: (a),(c) Without third-order dispersion,the evolution of the temporal intensity profile (a) of chaos states and the corresponding comb spectrum (c);(b),(d) with third-order dispersion,the evolution of the temporal intensity profile (b) of soliton state and the corresponding comb spectrum (d).Temporal profile/comb spectrum at t=3000 ns are shown on the top of each panel.

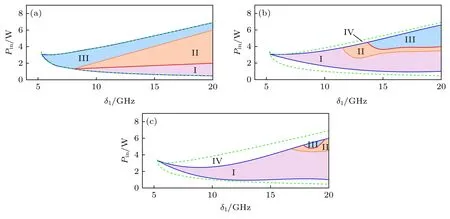
图4 三阶色散系数对光场稳定性和孤子存在状态的影响 (a) d13=0;(b) d13=—0.0563;(c) d13=—0.0938.I,稳定孤子域(包含单孤子态和双孤子态);II,时域振荡域(呼吸孤子态);III,混沌域;Ⅳ,连续波域Fig.4.Influence of different third-order dispersion coefficients on the stability region and soliton state: (a) d13=0;(b) d13=—0.0563;(c) d13=—0.0938.I,stable soliton region (including single soliton and multi soliton);II,time domain oscillation domain(breathers soliton);III,chaotic domain;Ⅳ,continuous wave domain.

3.2 各阶色散及其组合对光谱特性的影响

高阶色散的存在会导致色散波的产生,从而造成光频梳的频谱特性发生变化,并且影响腔内孤子峰值功率.这部分研究不同阶色散及其组合对光频梳光谱特性参数的影响.首先研究三阶色散对腔内光场产生的影响,具体的仿真参数为δ1=120 m—1,Pin=10 W,k12=—20 ps2/km,d13=—0.7506.其中,图5(a)和图5(c)分别展示了腔内光场分布和时域演化,图5(b)和图5(d)展示了腔内光谱和光谱演化图.从图5(a)可以看出,相较于仅考虑二阶色散的情况,三阶色散的存在使得孤子的时域形状变成非对称形态,一端带有振荡的辐射尾,孤子发生时域漂移,其传播速度改变.这种扰动的孤子态对应非对称的克尔光谱,如图5(b)和图5(d)所示,在孤子载波频率的蓝端约8.512 THz 处产生了一个光谱包络的极大值点,即色散波,该色散波对应于克尔光频梳功率和相位的跳变,是三阶色散诱导切伦科夫辐射的结果.色散波的光谱位置wd可以通过相位匹配条件计算得到,后文将展开讨论.

其次,研究四阶色散对耦合双环系统内光场分布和光谱特性的影响.在三阶色散的基础上,设置参量d13=—0.7506,d14=3.8×10—3(正四阶色散)/d14=—3.8×10—3(负四阶色散),并给出了正/负四阶色散的仿真结果,分别见图6 和图7.比较图5(b)与图6(b),可以发现包含正四阶色散项的梳状光谱色散波更加明显,功率得到了加强,正四阶色散的存在增强了色散波.而负四阶色散的情况则有所不同,与图5(b)相比较,图7(b)中的色散波受到了明显的抑制,表明负四阶色散能够抑制色散波的产生.同时,比较图5(c)和图6(c)可以看出,图6(c)所展示的腔内孤子漂移速度更慢.这可能是因为正四阶色散的存在改变了色散波的角频率,从而导致孤子漂移速度减小[28].需要注意的是,正四阶色散同时增强了光谱的长波长和短波长分量,提高了光频梳的带宽.另一方面,可以利用四阶色散改善孤子腔内克尔光频梳的光谱,从而得到更符合实际的克尔光频梳光谱包络.

图5 三阶色散对耦合微环腔内光场分布和光谱演化的影响 (a) t=5000 ns 时腔内的光场分布;(b) t=5000 ns 时腔内光谱图;(c) 孤子的时域演化图;(d) 孤子的光谱演化图Fig.5.Influence of third-order dispersion on the optical field and spectrum of coupled micro-ring resonators: (a) Optical field distribution in the cavity at t=5000 ns;(b) intracavity optical spectrum at t=5000 ns;(c) temporal evolution of solitons;(d) optical spectrum evolution of solitons.

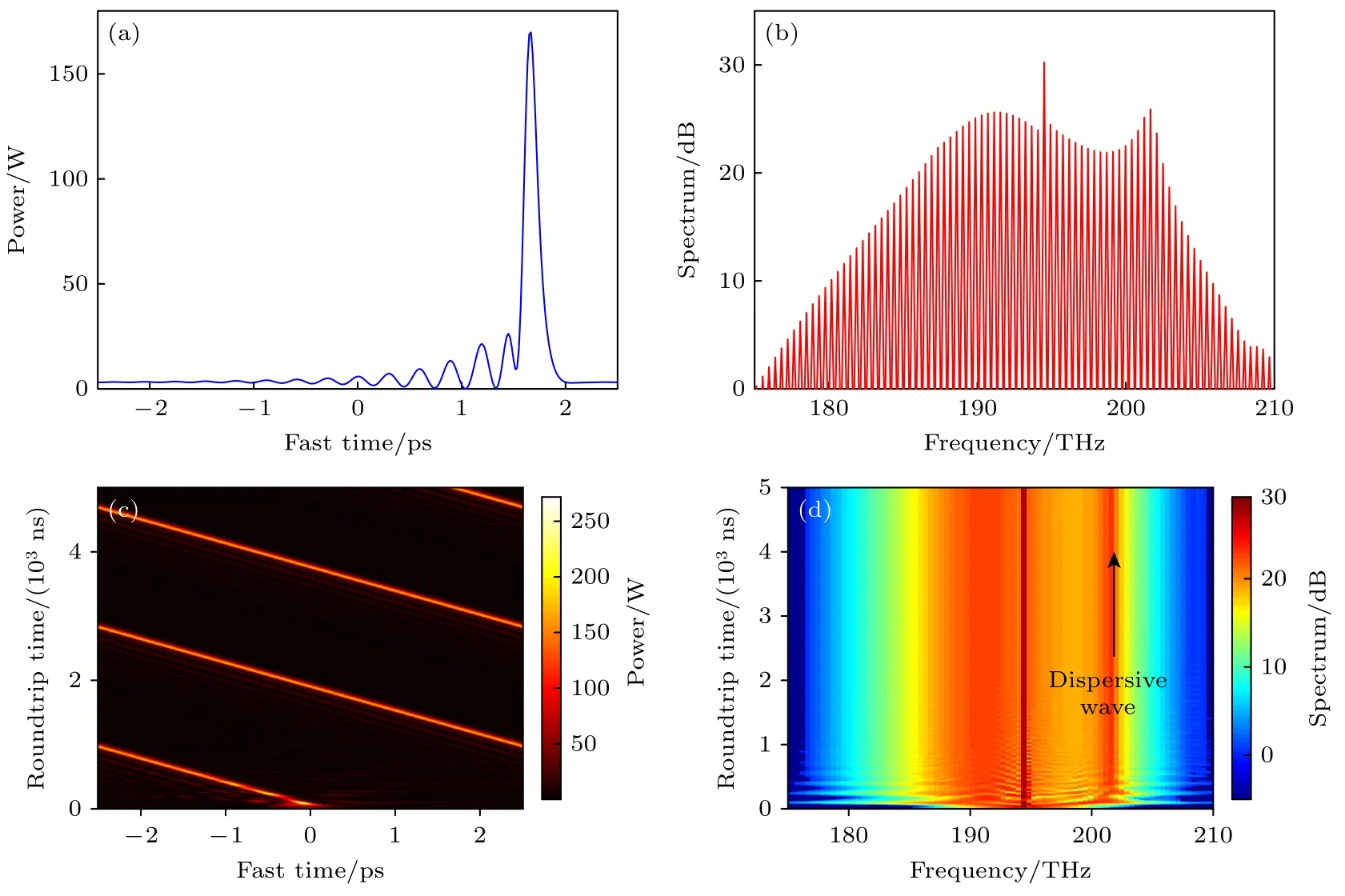
图6 正四阶色散对耦合微腔光频梳的色散波增强作用 (a) t=5000 ns,腔内的光场分布;(b) t=5000 ns,腔内光谱图;(c) 孤子的时域演化图;(d) 孤子的光谱演化图Fig.6.Impact of positive fourth-order dispersion on comb in coupled microcavities: (a) Optical field distribution in the cavity at t=5000 ns;(b) intracavity optical spectrum at t=5000 ns;(c) temporal evolution of solitons;(d) optical spectrum evolution of solitons.

图7 负四阶色散对梳状光谱色散波的抑制作用 (a) t=5000 ns,腔内的光场分布;(b) t=5000 ns,腔内光谱图;(c) 孤子的时域演化图;(d) 孤子的光谱演化图Fig.7.Suppression of dispersion waves of comb spectrum by negative fourth-order dispersion: (a) Optical field distribution in the cavity at t=5000 ns;(b) intracavity optical spectrum at t=5000 ns;(c) temporal evolution of solitons;(d) optical spectrum evolution of solitons.

图8 展示了五阶色散对双耦合微环腔内光场及光谱演化的影响,在负四阶色散的基础上,设置参量d15=7.6108×10—4.可见,五阶色散改变了孤子的漂移方向,与仅考虑三阶色散和四阶色散的情况相比,漂移速度变慢.值得注意的是正五阶色散能在孤子载波频率的红端产生色散波,如图8(b)和图8(d)所示.进一步,我们发现五阶色散参数的变化能够调控微腔孤子漂移的方向和速度,如图9所示,仿真参数为δ1=120 m—1,Pin=10 W,k12=—20 ps2/km,d13=—0.7506,d14=—3.8×10—3.为了定量表示孤子漂移速度的改变,本文定义孤子漂移速度V为光孤子脉冲在腔内位置的变化量与光场演化时间的比值,并研究腔内孤子漂移速度随五阶色散参数变化的定量关系.图10 展示了三阶色散和四阶色散相对系数保持不变的情况下,五阶色散相对系数d15从3.0443×10—4(图9(a))增大到4.5665×10—4(图9(c))的过程中,腔内孤子漂移方向的变化情况以及漂移速度大小的改变情况.从图10 可看出,当d15从3.0443×10—4逐渐增长到3.6532×10—4时,孤子漂移方向向左,漂移速度大小逐渐减缓;当d15=3.6532×10—4时,孤子几乎不发生漂移,其漂移速度十分接近0.d15从3.6532×10—4增长到4.5665×10—4过程中,孤子漂移速度逐渐变快并且漂移方向改变为向右漂移.这意味着我们可以通过控制微腔五阶色散的大小调控光孤子漂移的速度和方向,比如在三阶色散较大的情况下,通过调控五阶色散大小能够产生不发生时域漂移的孤子.这一结果对于腔内孤子的漂移方向、漂移速度以及孤子时域位置的精确调控有潜在价值.

图8 五阶色散对耦合微腔光频梳的影响 (a) t=5000 ns 时腔内的光场分布;(b) t=5000 ns 时腔内光谱图;(c) 孤子的时域演化图;(d) 孤子的光谱演化图Fig.8.Impact of positive fifth-order dispersion on comb in coupled microcavities: (a) Intracavity field distribution in the cavity at t=5000 ns;(b) intracavity optical spectrum at t=5000 ns;(c) temporal evolution of solitons;(d) optical spectrum evolution of solitons.

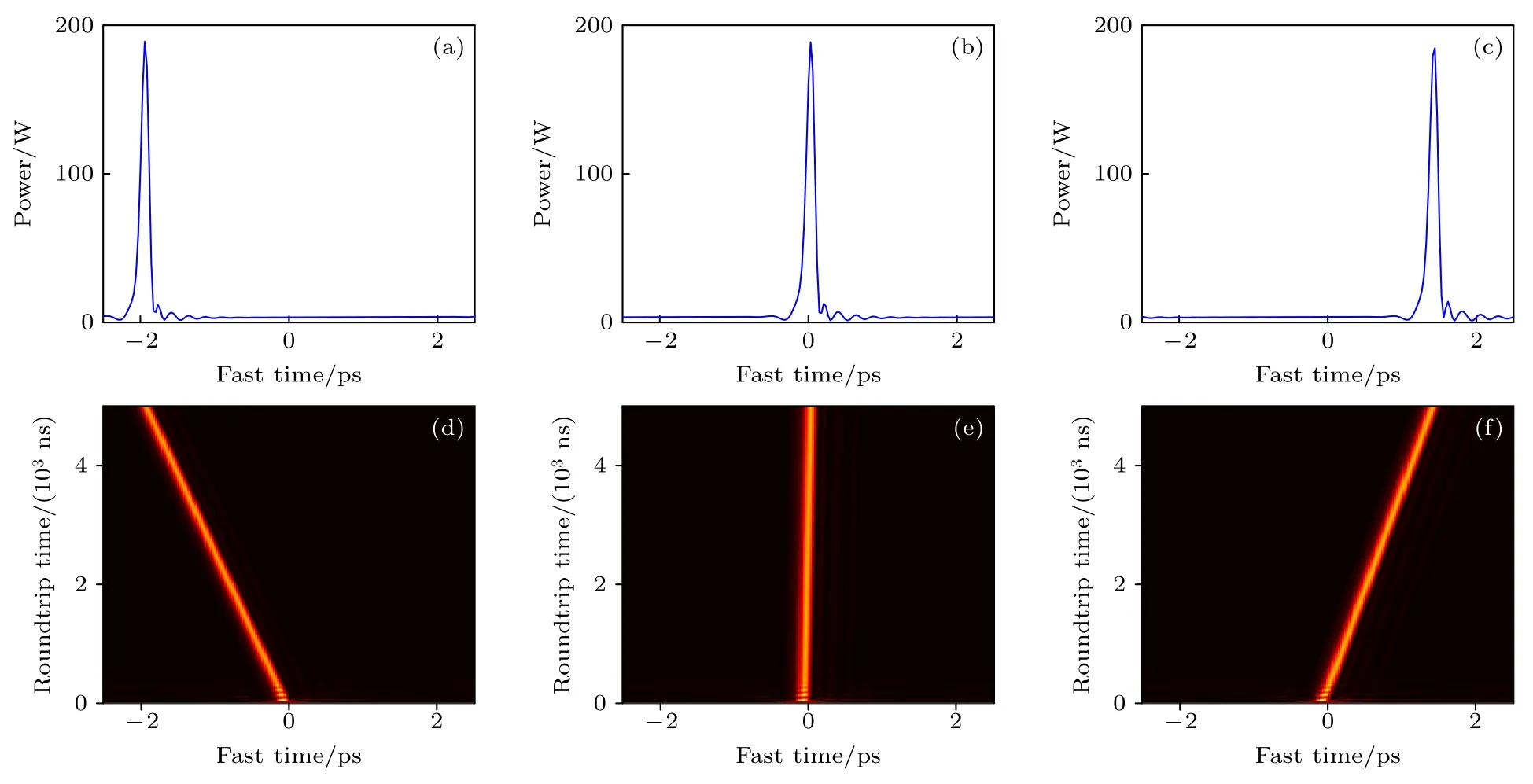
图9 五阶色散对孤子漂移方向的控制作用 (a)—(c) t=5000 ns 时,d15=3.0443×10—4 (a),3.6532×10—4 (b),4.5665×10—4 (c)条件下腔内光场分布;(d)—(f) 与图(a)—(c)对应的时域演化图和孤子漂移Fig.9.Control of soliton drift direction by fifth-order dispersion: (a)—(c) Intracavity field distribution of soliton at t=5000 ns and d15=(a) 3.0443×10—4,(b) 3.6532×10—4,(c) 4.5665×10—4;(d)—(f) corresponding temporal evolution and soliton drift of panel (a)—(c).

图10 五阶色散相对系数d15 对孤子漂移速度的影响Fig.10.Effect of the fifth-order dispersion relative coefficient d15 on the soliton drift velocity.

考虑到在三阶色散作用下腔内光梳能够激发色散波,使得腔内孤子发生漂移如图5(b)和图5(c)所示,分析了三阶色散和五阶色散使得孤子发生漂移的情形,并对比了两种色散的作用.图5 中三阶色散使得孤子向左漂移,在仿真过程中,尚未观察到调控三阶色散使得孤子向右漂移的现象,这与单腔耦合系统的结果不同,可能是由双微腔模式耦合导致的自发对称性破缺导致的结果.而图9 中五阶色散对于孤子漂移的调控可以使得孤子向左、向右甚至不发生漂移,这种调控作用是建立在三阶色散基础上,其适用在形状等因素限制下使得三阶色散值无法发生较大改变时的情形.在微腔孤子时域演化方面,三阶色散和五阶色散均能够对孤子漂移造成影响.但三阶色散对孤子漂移的影响程度大于五阶色散,因此五阶色散可以适用于三阶色散值不能大幅改变情况下精细调控孤子的漂移方向与速度.此外,对于腔内光频梳演化而言,三阶色散的存在能够扩大其稳定域,使得呼吸子与混沌稳定为孤子状态.在频率域,负三阶色散的引入,会诱导切伦科夫辐射打破局部结构的对称性,再激发色散波.而正五阶色散的加入可以改变色散波的位置.总体来说,所有的高阶色散共同修饰了色散曲线包络并直接导致了不同色散波位置,最终影响了频率梳的光谱包络.

在实际微腔系统中,通常的情况是二阶色散和四阶色散并存,因此接下来研究二阶色散与四阶色散的竞争作用对光频梳光谱的影响,仿真参数为δ1=120 m—1,Pin=10 W,k12=—60 ps2/km,d14=—2.817×10—6.图11(a)—(c)展示了仅包含负二阶色散的情况下孤子腔内的光场、梳状光谱及时域演化图,图11(d)—(f)展示了仅包含负四阶色散的情况,而图11(g)和图11(h)展示了二阶色散和四阶色散共同作用的情况.可以看出,对于上述3 种群速色散情况均可以观察到稳定的锁模克尔光频梳.通过监测脉冲在腔内振荡数万圈后保持其形状不变确认其实现锁模态,即腔内光场脉冲的宽度和峰值功率不随时间振荡,且光谱保持稳定(见图11(c),(f),(i)).二阶色散和四阶色散的竞争产生了功率相近、频谱包络不同的克尔光梳.由于采用了负四阶色散,和正四阶色散不同,它会抑制色散波产生和频率漂移,从而得到对称的克尔孤子频梳.负二阶色散对应的光谱大约在60 THz 频谱范围内梳齿功率较为一致,梳齿功率随波长变化不大,呈现“平顶”光谱,如图11(b)所示;而负四阶色散产生的光谱随着其远离泵浦频率功率衰减较严重,表现出“鼓形”光谱如图11(e)所示;当两种色散成分共存时,由于二阶色散和四阶色散的竞争效应,产生光谱包络如图11(h)所示,相比于图11(e),其幅度值大小明显下降,幅度变化趋势较接近“鼓形”光谱,不同于图11(b)所呈现的“平顶”光谱.

图11 二阶色散与四阶色散的竞争作用对光梳光谱的影响 (a)—(c) 仅含有二阶色散时腔内光场(a)、光谱(b)和时域(c)演化图;(d)—(f) 仅含有四阶色散时腔内光场(d)、光谱(e)和时域(f)演化图;(g)—(i) 二阶和四阶共同作用下腔内光场(g)、光谱(h)和时域(i)演化图Fig.11.Influence of the competition between second-order and fourth-order dispersion on comb spectra: (a)—(c) Intracavity optical field (a),spectrum (b) and time domain (c) with second-order dispersion;(d)—(f) intracavity optical field (d),spectrum (e) and time domain (f) with fourth-order dispersion;(g)—(i) intracavity optical field (g),spectrum (h) and time domain (i) with second-order and fourth-order dispersion.

根据前面的分析,各高阶色散对孤子腔内光频梳的色散波频谱位置、色散波强度有不同影响,而在实际微腔系统中通常是各阶色散组合的情况,因此下面研究不同阶高阶色散项组合对于光频梳光谱特性的影响.图12 展示了高阶色散组合情况下,在最大泵浦失谐处的相位匹配曲线和腔内梳状光谱.这里我们利用相位匹配参数Δδ来表征光频梳的生成,

其中,γ为泵浦模式的线宽,P1s为腔1 内孤子的峰值功率,wd为色散波频率,ws为孤子的载波频率.(6)式的相位匹配条件与高阶色散作用下色散波的产生过程相对应,因为孤子受到高阶色散作用下,会将一部分能量转移到特定频率的色散波中,这个特定频率由相位匹配条件决定,该相位匹配条件要求色散波与孤子的相速度相同.图12(a)和图12(c)分别展示了考虑二阶、三阶和四阶色散的相位匹配曲线和对应的梳状光谱,参数设为:δ1=120 m—1,Pin=10 W,k12=—20 ps2/km,d13=—0.0113,d14=2.535×10—5.可以看出,图12(a)中的相位匹配点与图12(c)中色散波形成的频谱位置匹配良好.在这3 阶色散的共同作用下,在载波频率的蓝端产生了较强的色散波,可能源于正四阶色散对色散波的增强作用.图12(b)和图12(d)展示了考虑二阶到五阶色散时的相位匹配曲线,这里采用负四阶色散,参数设为:d13=—0.1126,d14=—8.4502×10—7,d15=4.5665×10—5(其余参数保持不变).同样地,其相位匹配点与色散波的产生频谱位置匹配.与仅考虑二阶、三阶和四阶色散情况不同的是,其色散波产生于载波频率的红端.根据图8 的结果和讨论,正五阶色散会在孤子载频的红端产生色散波,其远离载波频率,且功率低[29],因此此处激发的色散波在光梳载波频率的红端[30].这表明考虑d14和d15等高阶色散项对于宽光谱光频梳的光谱特性,特别是色散波的频谱位置有重要影响.

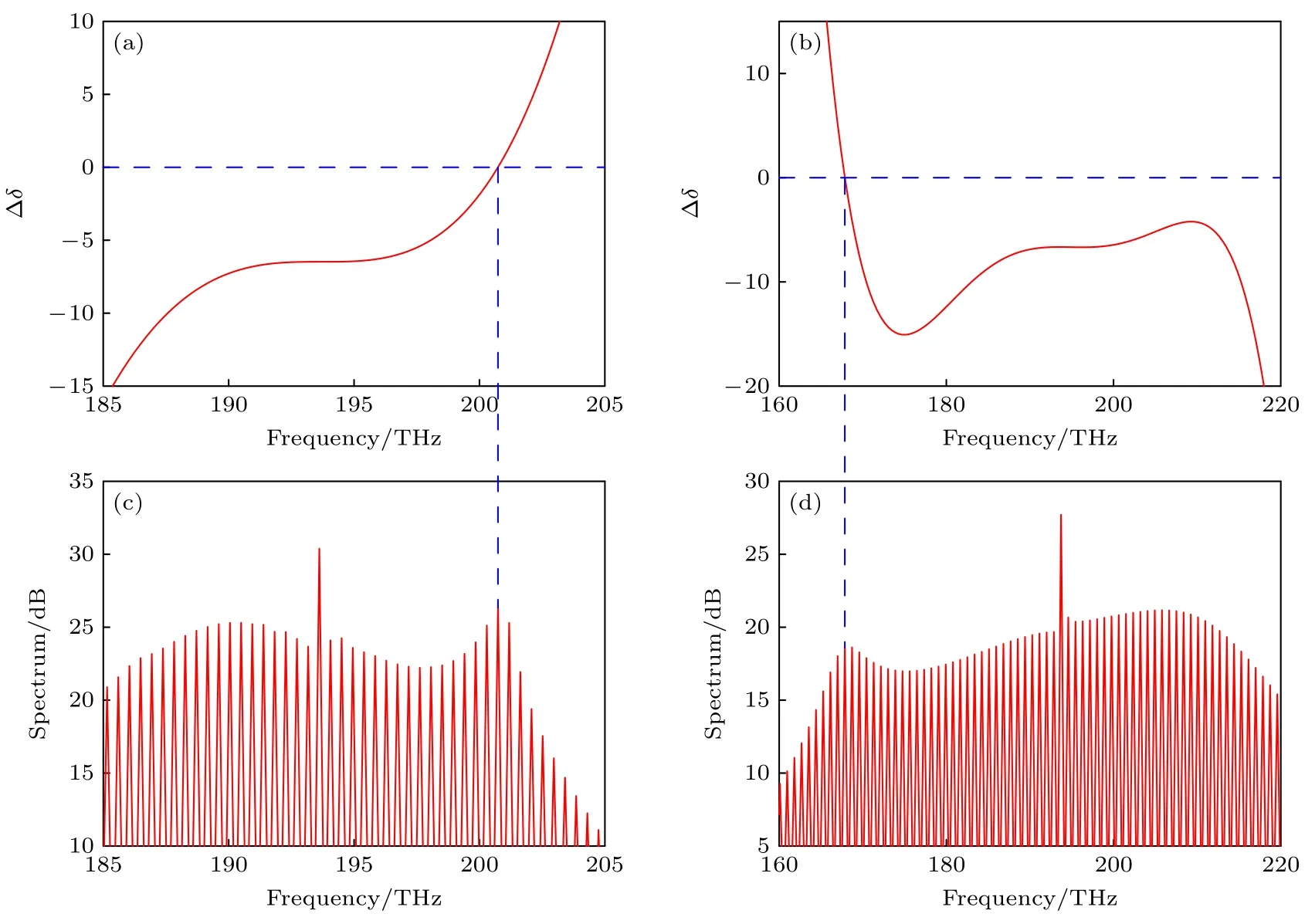
图12 各高阶色散组合对光频梳光谱的影响 (a) 包含二阶、三阶和四阶色散的相位匹配曲线;(b) 包含二阶到五阶色散的相位匹配曲线;(c),(d)与(a),(b)色散波位置对应的光谱图Fig.12.Influence of combined high-order dispersion on spectral characteristics: (a) Phase matching curve of second,third and fourth order dispersion;(b) phase matching curve of 2nd—5th order dispersion;(c),(d) spectrogram corresponding to dispersion wave position in (a),(b).

3.3 高阶色散对光谱特性的影响

接下来,定量分析高阶色散对光频梳光谱特性参数的影响.图13 展示了考虑二阶和三阶色散以及考虑二阶、三阶和四阶色散两种情况下孤子最大失谐δmax和腔内峰值功率与泵浦功率Pin之间的关系,色散参数设为:k12=—80 ps2/km,d13=—0.1876,d14=3.1688×10—4.通过对Pin与该功率下稳定孤子态的最大失谐δmax进行线性拟合,可以看出,δmax随Pin的增加呈线性增加,且在包含四阶色散项以及不包含四阶色散项这两种情况下都能很好地满足线性关系,如图13(a)和图13(b)所示;图13(c)和图13(d)展示了腔内孤子峰值功率P1s与Pin的关系.可以发现,当Pin＜300 W 时,其随Pin的增加基本呈线性增长趋势;而当Pin＞300 W 后,图13(c)中腔内峰值功率增加变缓,并逐渐趋于平稳,并偏离拟合直线.在四阶色散的作用下,尽管当Pin较低时,图13(d)腔内峰值功率(226 W)比图13(c) (225 W)略高,但随着输入Pin的增大,在Pin=375 W 时,图13(d)腔内峰值功率(235.5 W)却要低于图13(c)中腔内峰值功率(237.0 W).这可能因为输入Pin被转换成孤子和色散波的能量,当Pin增大时,辐射的色散波功率也增大,且色散波功率与孤子功率的比例增大,使得孤子的峰值功率低于理想的预测值,这解释了图13(c)和图13(d)中腔内峰值功率曲线随着Pin的增大斜率逐渐变小.此外,正四阶色散会增强色散波,造成色散波功率与孤子功率的比例相比仅考虑二阶和三阶色散的情况进一步增大,从而使得图13(d)中的腔内峰值功率曲线斜率总体上要小于图13(d)中腔内峰值功率曲线斜率,这也是源于色散波对光频梳光谱产生的影响.

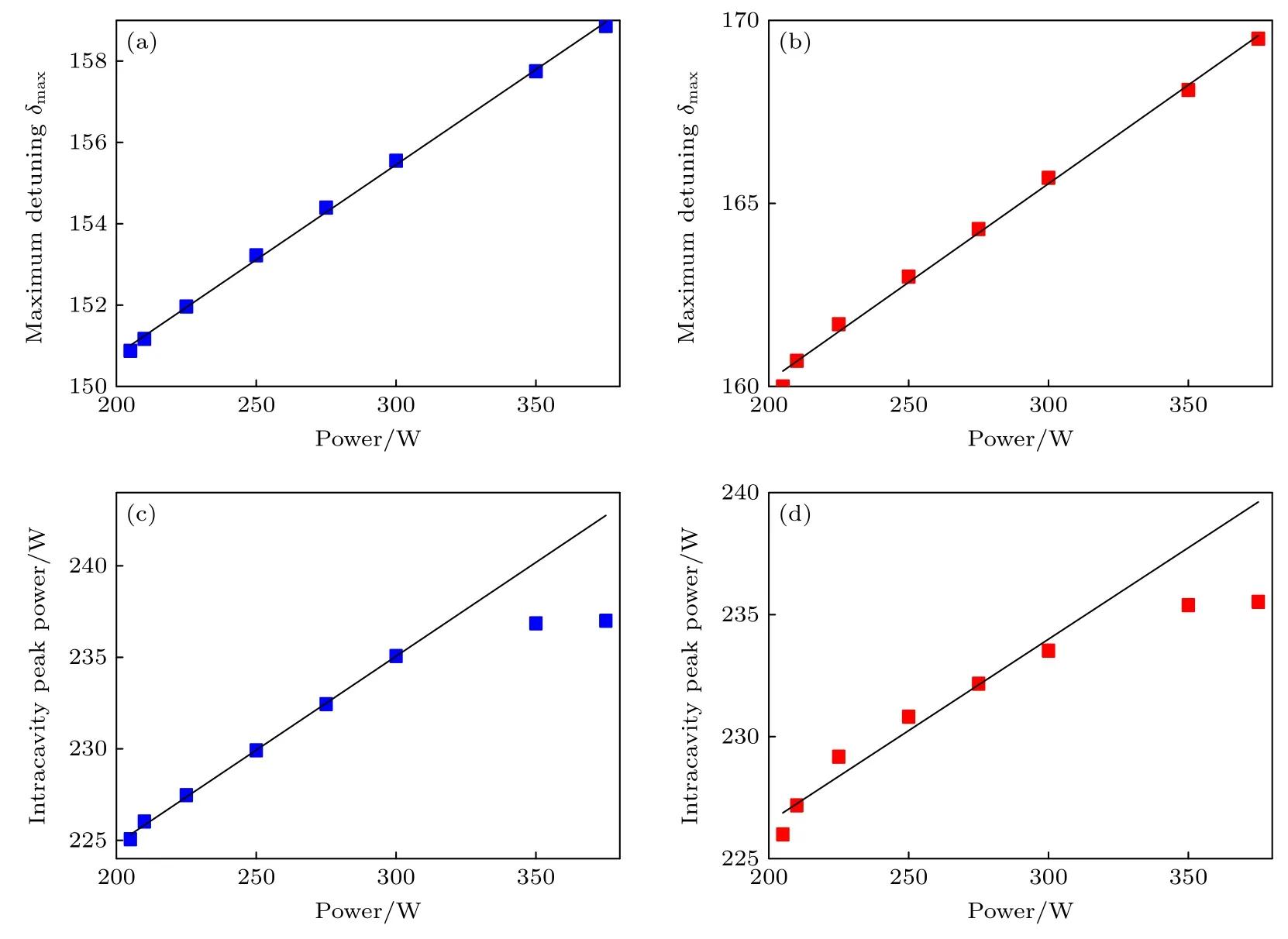
图13 各阶色散组合对光谱特性的影响 (a) 包含二阶和三阶色散时δmax 与Pin 的关系;(b) 包含二阶、三阶和四阶色散时δmax 与Pin 的关系;(c) 包含二阶和三阶色散时腔内峰值功率与Pin 的关系;(d) 包含二阶、三阶和四阶色散时腔内峰值功率与Pin 的关系Fig.13.Effect of various dispersion combinations on spectral characteristics: (a) Relationship between δmax and Pin with second and third order dispersion;(b) relationship between δmax and Pin with second,third and fourth order dispersion;(c) relationship between peak power in cavity and with second and third order dispersion;(d) relationship between peak power in cavity and Pin with second,third and fourth order dispersion.

最后讨论泵浦功率对色散波位置的影响.在单个微腔内,由高阶色散诱导的切伦科夫辐射引起了光谱中色散波的产生,其频谱位置与泵浦功率有关[19],下面证明这一效应在耦合微腔系统中也存在,并研究频移大小与高阶色散项的关系.图14(a)展示了考虑二阶和三阶色散、二阶到四阶色散和二阶到五阶色散情况下仿真得到的色散波频谱位置随泵浦功率的移动.分别对不同情况下仿真得到的色散波位置进行线性拟合(仿真色散参数设为d13=—0.7506,d14=5.1×10—3),得到如图14(a)所示的红色(二阶和三阶)、蓝色(二阶到四阶)和黑色直线(二阶到五阶).从图14(a)可知,随着Pin的增加,色散波频率wd向长波长方向移动,这一趋势也可以从(6)式中看出.在仅考虑二阶和三阶色散情况下,随Pin的增加,色散波频谱位置的减小并不明显;加入四阶色散项后,由于正四阶色散对色散波的促进作用,色散波频谱位置产生了较大的移动,如图蓝线所示,当Pin从5 W 增加到34 W 时,wd从203.8 THz 移动到192.5 THz;而在二阶到五阶色散存在的情况下,色散波的频谱位置随Pin增加产生了更大的频移,当Pin从7 W 增加到32 W 时,wd从167.9 THz 移动到154.8 THz.仿真结果表明,色散波频谱位置随Pin的增加向长波长方向移动,且频移大小与高阶色散项的阶数有关.此外,随着Pin的增加色散波的功率也在增加,并且色散波功率的增加使得光频梳包络的中心偏离Pin约3.5 THz (图14(c)),这种现象称为“光谱反冲”[31].光谱反冲现象可以通过孤子动量理解,孤子动量相当于整个光频梳的质心,,是频率wm处的光谱分量幅值,m是相对于泵浦模式的模式数.在不考虑拉曼效应引起孤子自频移的情况下,稳态光频梳的孤子动量等于零[32,33].因为色散波仅产生于光频梳光谱的一侧(蓝端或红端),光谱质心偏离零点,因此在其作用下,整个光谱包络会向色散波产生的反向频移,以补偿色散波对于孤子动量的影响.“光谱反冲”现象在色散波较弱的情况下变弱,如图14(b)所示.

图14 (a) 随Pin 的增加,不同高阶色散组合情况下wd 的变化;(b) Pin=5 W 和(c) 15 W 时,包含二阶到四阶色散情况下的腔内梳状谱Fig.14.(a) Under the condition of different orders of high-order dispersion,the variation of wd with the increase of Pin;(b),(c) the intracavity comb spectrum with 2nd—4th order dispersion at (b) Pin=5 W and (c) 15 W.

4 讨论与总结

本文在包含高阶色散项的耦合非线性薛定谔方程的基础上,研究了高阶色散对双耦合微环腔中克尔光频梳的稳定性及其光谱特性参数的影响.研究结果表明,高阶色散的加入使得参量空间的稳定域扩大,三阶色散使得孤子不稳定性被抑制,腔内的呼吸孤子态和混沌态转变为稳定的孤子态.随着三阶色散的增大,稳态解存在域中的混沌域不断缩小且向失谐更大处移动,呼吸孤子域也逐渐缩小,并向功率更大处移动,而稳定孤子域不断扩大.另一方面,高阶色散的作用使得孤子腔内产生色散波,不同阶色散对于色散波的频谱位置、强度大小产生影响,导致光频梳光谱特性发生变化.三阶色散和正四阶色散项可以诱导切伦科夫辐射,在光谱蓝端产生增强的色散波;而负四阶色散项会抑制色散波的产生,得到较对称的孤子频梳;五阶色散能够控制孤子的漂移方向及速度,且色散波产生于光谱的红端.色散波的产生进一步影响泵浦功率转换成的色散波功率与孤子功率的比例,对梳状光谱结构包括最大失谐、腔内脉冲峰值功率产生影响.此外,高阶色散项的组合使得色散波频谱位置产生频移,频移大小随泵浦功率的增加而增加,且与高阶色散项的阶数有关.对比单腔结构,在双微腔结构使得了泵浦-孤子转换效率得到了巨大的提升,同时,腔内高阶色散的影响使得参量空间稳定域增大,不稳定性得到了抑制,双耦合微腔结构在更大的参数空间域中实现了稳定孤子态.并且对于色散波位置而言,改变泵浦功率,双耦合微腔中激发色散波的频域位置变化范围要比单微腔更宽.高阶色散作用下,双耦合微腔内孤子动力学的研究对于调控孤子的形成和色散波的频谱位置有较大的意义.这些结果将为基于耦合微环微腔光频梳的光钟、超快精密测量等相关应用开辟新的可能性.