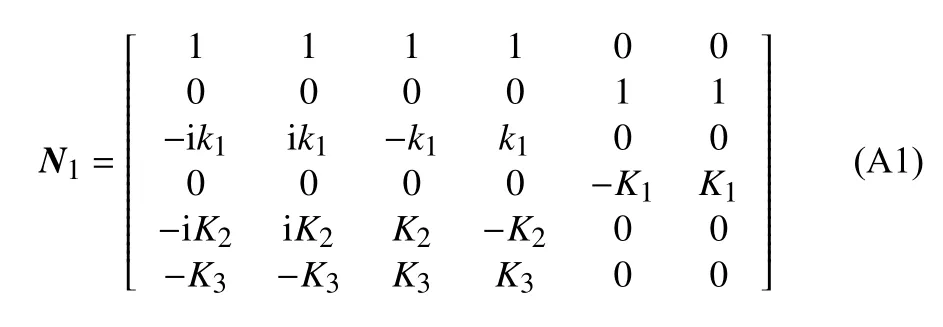弯曲波彩虹捕获效应及其在能量俘获中的应用1)
王芳隆 沈一舟 徐艳龙 周生喜 杨智春
(西北工业大学航空学院,西安 710072)
引言
在力学领域,结构中的弹性波是一个非常重要的研究对象,相关研究成果可以促进结构健康监测、振动控制以及能量俘获等领域的发展[1].近些年来,可以实现波传播超常操控的人工结构,如超材料(metamaterials)[2-4]、声子晶体(phononic crystals)[5-6]和声学黑洞(acoustic black holes)[7-10]等,得到了广大研究者的关注.此外,由Tsakmakidis等[11]于2007 年在电磁波领域首次提出的彩虹捕获(rainbow trapping)结构也推广到了弹性波领域.弹性波彩虹捕获结构是一种梯度结构,也有学者将其称为啁啾声子晶体(chirped phononic crystals)[12-13],其元胞的参数沿着波传播方向梯度变化.不同频率的弹性波在此种结构中传播时会在相应的不同位置停止向前传播,这是弹性波彩虹捕获效应的空间分频现象.在弹性波停止向前传播的区域,波场能量明显高于其他区域,这是弹性波彩虹捕获效应的波场能量增强现象.
2015 年,Xu 等[14-15]先通过有限元仿真研究了瑞利波的彩虹捕获效应,又通过传递矩阵法理论研究了水平剪切波(SH 波)的彩虹捕获效应.这是弹性波彩虹捕获效应最早的研究成果.同一年,Zhao 等[16]研究了结构梁中兰姆波的彩虹捕获效应.2017 年,Tian 等[12]通过有限元仿真和实验研究了具有梯度槽的板中的兰姆波彩虹捕获效应.Li 等[17]通过电磁波和声波领域中常用的高阶波导模式理论(highorder waveguide modal theory)研究了SH 波的彩虹捕获效应.
从2020 年开始,部分学者将能量俘获与弹性波彩虹捕获效应结合起来,以期探索出弹性波能量俘获的新方法[18-23].英国帝国理工学院的Craster 课题组[18-22,24-28]自2016 年以来在弹性波彩虹捕获效应领域开展了系统的研究工作,在利用彩虹捕获效应进行能量俘获方面取得了一定的成果[18-22].2020 年,Ponti 等[18-19]通过在基体上添加高度梯度变化的谐振杆构建了一个用于能量俘获的彩虹捕获结构.他们将十字形的压电层合梁放置在谐振杆的顶端,通过谐振杆将基体中的弹性波转化为压电层合梁的振动,从而实现对薄梁中的A0 兰姆波和半无限体中的表面波的能量俘获.通过数值仿真和实验,他们证明了此结构相较于没有梯度谐振杆的结构具有更好的能量俘获效果,这是彩虹捕获结构在能量俘获中应用的首次成功尝试.Chaplain 等[20]通过非对称的梯度元胞提出了彩虹反射的概念,解释了其与彩虹捕获的区别,并将它们应用在压电能量俘获研究中.结果表明,彩虹捕获结构相对于彩虹反射结构可以俘获更多的弹性波能量.同一年,Chaplain 等[21]将梯度结构与拓扑绝缘体领域的SSH (Su-Schrieffer-Heeger)模型结合,研究了其彩虹捕获效应,并将其应用于压电能量俘获研究.2021 年,De Ponti[22]发表的专著Graded Elastic Metamaterials for Energy Harvesting,系统地总结了近些年波操控结构在能量俘获领域的研究现状,并着重介绍了2020 年以来利用彩虹捕获结构进行能量俘获的研究工作.
作为弹性波操控领域一个正在兴起的研究方向,国内外关于弹性波彩虹捕获效应的研究才刚刚起步.一方面,弹性波彩虹捕获效应的产生机理还有待进一步揭示.另一方面,彩虹捕获结构的能量俘获效果随入射波频率的变化规律还没有深入研究.本工作通过所设计的梯度结构梁,研究了弯曲波彩虹捕获效应及其在压电能量俘获中的应用.在第1 节中,通过传递矩阵法获得了梯度结构梁元胞能带结构解析解,并利用解析解从波数和群速度变化的角度揭示了弯曲波彩虹捕获效应的产生机理;第2 节通过有限元仿真和实验验证了弯曲波彩虹捕获效应的空间分频现象和波场能量增强现象;第3 节通过有限元多物理场耦合仿真和实验,研究了粘贴PVDF压电薄膜的梯度结构梁相对于均匀梁的弯曲波能量俘获效果及其随入射波频率的变化规律;第4 节对全文进行了总结.
1 梯度结构梁元胞能带结构分析
1.1 梯度结构梁
本文设计的梯度结构梁,由1 个基梁和16 个在基梁上垂直布置的立柱组成,如图1(a)所示.立柱的高度从左到右依次递增,第1 个立柱的高度为H1=6.0 mm,第n个立柱的高度为Hn=H1+(n-1)h,增量h为0.4 mm.基梁的厚度T和立柱的厚度b都是2 mm;基梁和立柱的宽度都是20 mm;梯度结构梁的晶格常数D是12 mm.材料选用光敏树脂,其力学性能参数根据Shen 等[29]提出的方法测得: 弹性模量Y为2.067 8 GPa,密度ρ为1110 kg/m3.
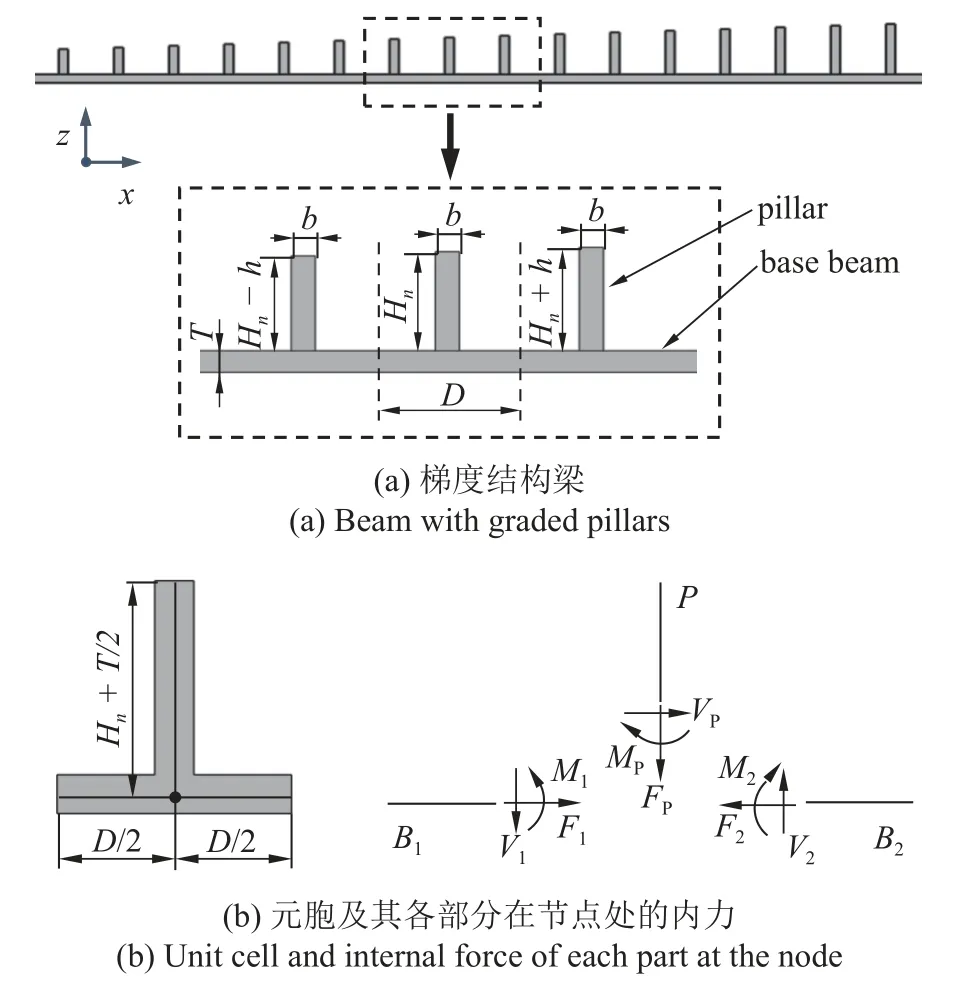
图1 梯度结构梁及其元胞Fig.1 Beam with graded pillars and its unit cell
1.2 元胞能带结构的解析模型
基于Cao 等[30]的研究,本文通过传递矩阵法建立梯度结构梁元胞能带结构的解析模型.后面将以能带结构为工具分析弯曲波彩虹捕获效应的产生机理,并预测弯曲波彩虹捕获效应在梯度结构梁中的发生位置和相应的频带.
任取梯度结构梁的一个元胞,并用中性轴将其简化,如图1(b)左图所示.简化后的立柱的长度为Hn+T/2.在立柱与基梁的连接结点处,可以将元胞分为两个基梁部分B1和B2和一个立柱部分P.图1(b)右图也表示出了三部分在节点处的内力.
由于基梁和立柱的相互作用,元胞中同时存在弯曲波和纵波.基于弹性波导理论[1],梁中的弯曲波和纵波的控制方程分别为
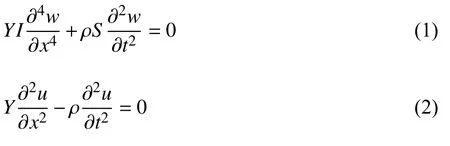
式中,Y为弹性模量;I为截面惯性矩;ρ为密度;S为截面积;w为横向位移,即挠度;u为轴向位移.
对应于元胞的三部分B1,B2和P,方程(1)和方程(2)的通解分别可以表示为

通解的复系数可以表示成一个向量,称为系数向量

对于元胞的任一部分的任一截面上都存在六个物理量,它们分别是: 挠度w,轴向位移u,转角 φ,轴力F,剪力V和弯矩M.可以将它们表示成一个向量,称为状态向量
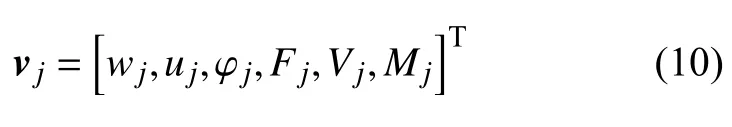
根据材料力学中梁的同一截面上位移与内力之间的关系,可以得出元胞同一部分的同一截面上状态向量与系数向量之间的关系
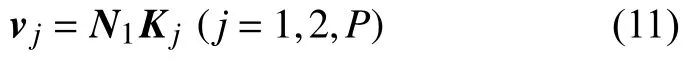
式中,N1为元胞同一部分的同一截面上状态向量和系数向量的传递矩阵[30].
在同一时刻,元胞的同一基梁部分(B1或B2)的左端面与右端面相差D/2 的传播距离,它们的状态向量之间仅相差由D/2 确定的相位因子.所以右端面的状态向量可以通过左端面系数向量表示
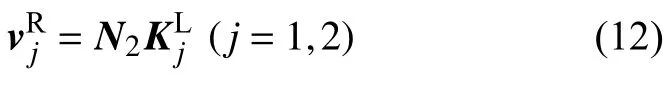
式中,N2为和之间的相位差传递矩阵[30];上标R 和L 分别表示B1或B2的左端面和右端面.
由B1,B2和P在节点处的内力平衡条件和连续性条件以及P在自由端的内力边界条件,可以得到复合系数向量K2P与B1右端面系数向量之间的关系

传递矩阵N1,N2和N3的具体形式详见本文附录,推导过程可以在参考文献[30]中找到.
联立方程式(11)、式(12)和式(14),可以得到B1左端面状态向量和B2右端面状态向量之间的关系
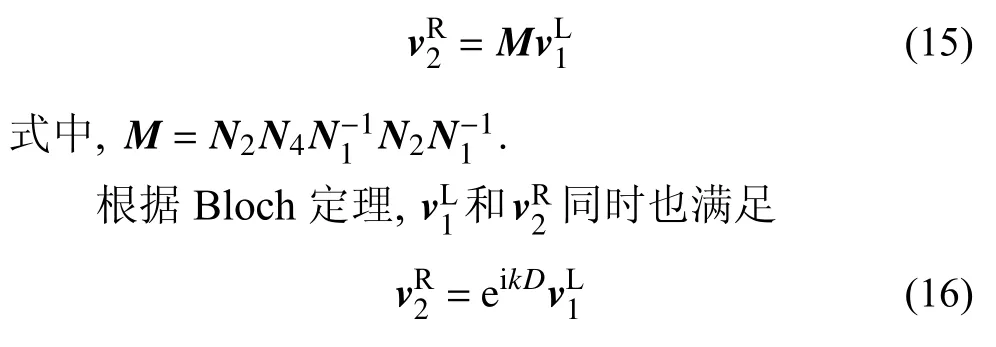
式中,k为Bloch 波数.
联立方程式(15)和式(16),可以得到特征方程
式中,E为六阶单位矩阵.
通过求解方程(17),可以得到在元胞中传播的弹性波的频率f和波数k之间的关系曲线,即色散曲线.这些色散曲线构成元胞的能带结构图.
1.3 弯曲波彩虹捕获效应机理
本文将16 个元胞在第一布里渊区[-π/D,π/D]内的一阶色散曲线解析解绘制在图2 中.各元胞的一阶色散曲线解析解由黑色曲线表示(其中第14 个元胞的一阶色散曲线解析解用绿色曲线表示).元胞的立柱高度越大,其一阶色散曲线就越低.以第1 个元胞为例来验证一阶色散曲线传递矩阵法解析解的精度,图中蓝色三角形点代表第1 个元胞的一阶色散曲线有限元梁单元解.可以看出,传递矩阵法解析解与有限元法梁单元解完全重合.为了描述弯曲波在梯度结构梁中传播时波数的变化过程,图中也绘制出了用灰色实线表示的均匀梁中弯曲波的色散曲线,以及用黑色水平虚线表示的等频率线,此等频率线代表待分析的入射波的频率.
在图2 的Ⅱ区域中,频率为水平黑色虚线的弯曲波在均匀梁中以红色实心圆点所表示的波数传播.弯曲波从均匀梁传进梯度结构梁后,遇到的立柱的高度越来越大,其波数沿着红色箭头逐渐从立柱高度较小的元胞的色散曲线所对应的波数转移到立柱高度较大的元胞的色散曲线所对应的波数,模式也逐渐从均匀梁中的弯曲波模式转变为元胞中的伪弯曲波模式[12].在这个过程中,其群速度越来越小.水平黑色虚线与第14 个元胞的色散曲线(图中绿色曲线)相切于红色空心圆点.此时弯曲波的群速度在第14 个元胞处变成了0,将这个切点称为零群速度点.由于波动量的守恒,弯曲波最终会在达到零群速度的元胞处反射回入射端.在反射时,波数k将会变为k-2π/D,即波数k将从π/D变为-π/D.这时候Ⅱ区域中的红色空心圆点转变成了Ⅰ区域中的红色空心圆点.在反射后,弯曲波遇到的立柱的高度越来越小,其波数,群速度以及模式的变化过程与入射时相反.在传出梯度结构梁后,弯曲波在均匀梁中反向传播.

图2 弯曲波彩虹捕获效应的产生机理Fig.2 Generation mechanism of rainbow trapping of flexural waves
通过以上分析可知,不同频率的弯曲波对应的达到零群速度的元胞不同,所以发生反射的位置不同.频率越低,对应元胞的立柱越高,发生反射的位置越靠后.于是,不同频率的弯曲波在沿着立柱高度增加的方向传播时,会在不同的元胞位置附近停止向前传播并发生反射.这是弯曲波彩虹捕获效应空间分频现象的产生原因.在发生反射的位置,弯曲波的群速度为0,所以其能量会在此处产生累积,另外,由于入射波和反射波的叠加,会使得发生反射的地方的波场能量明显高于其他区域.这是弯曲波彩虹捕获效应波场能量增强现象的产生原因.
为了将弯曲波频率与彩虹捕获效应发生的位置对应起来,把图2 中第n个元胞的零群速度点所对应的频率(简称为零群速度点频率)fn列在表1中.由于频率f满足fn+1<f<fn的弯曲波都会在第n个元胞位置附近发生彩虹捕获效应,所以为了方便进行有限元仿真和实验,选取fn和fn+1的中间频率fnn+1作为后面仿真和实验的弯曲波频率.
表1 元胞的零群速度点频率 fn和两相邻元胞零群速度点频率的中间频率Table 1 Zero group velocity point frequency fn of unit cells and intermediate frequency of zero group velocity point frequencies of two adjacent unit cells
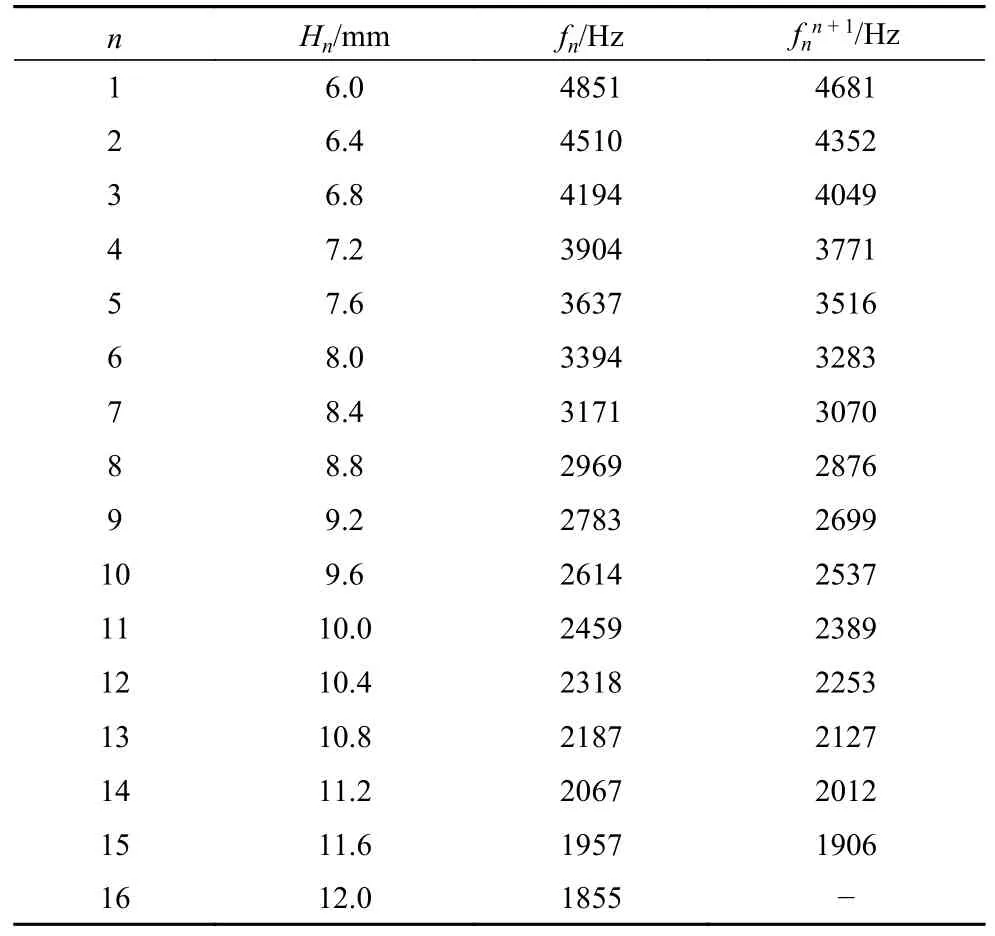
表1 元胞的零群速度点频率 fn和两相邻元胞零群速度点频率的中间频率Table 1 Zero group velocity point frequency fn of unit cells and intermediate frequency of zero group velocity point frequencies of two adjacent unit cells
2 弯曲波彩虹捕获效应
2.1 有限元仿真
基于前面所阐述的机理,本文在有限元软件COMSOL Multiphysics 中进行仿真分析,验证弯曲波彩虹捕获效应的空间分频现象和波场能量增强现象.
2.1.1 频域仿真
频域仿真模型如图3 所示.线源用于产生弯曲波.完美匹配层PML 用于吸收弯曲波,避免其在边界发生反射.

图3 频域有限元仿真模型(单位: mm)Fig.3 Finite element simulation model in frequency domain (unit: mm)
图4(a) 展示了弯曲波在基梁中的挠度幅值场(|w|).图中标出了梯度结构梁中部分立柱的位置.可以明显地看出空间分频现象: 不同频率的弯曲波传播到对应的元胞位置后,其挠度幅值分别迅速减小至零,即停止向前传播.除了空间分频现象,彩虹捕获效应还包含波场能量增强现象.图4(b)展示了基梁中的x向正应变(简称为正应变)场(|ε|).可以看出,在弯曲波停止向前传播的地方,能量得到了显著增强.

图4 弯曲波彩虹捕获效应Fig.4 Rainbow trapping of flexural waves

图4 弯曲波彩虹捕获效应(续)Fig.4 Rainbow trapping of flexural waves (continued)
2.1.2 时域仿真
本部分将通过时域仿真,模拟弯曲波在梯度结构梁中的传播过程,并验证波场能量增强现象的产生机理.由于时域仿真中没有PML,所以通过增加结构的整体长度,并让仿真时间小于弯曲波传播到边界所需的时间,来避免弯曲波在边界的反射.仿真中在线源处施加的位移载荷为5-cycle tone burst 函数,其时域表达式为
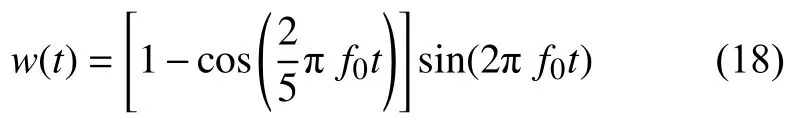
式中,f0为5-cycle tone burst 函数的中心频率.
图5展示了f0为2876 Hz 的弯曲波在梯度结构梁中的传播过程.以0.2t0(t0=1/f0)为时间步长截取相应时域仿真结果的基梁正应变云图,并将云图按时间的先后顺序进行组合就得到了图5.可以看出弯曲波的反射和波场能量增强现象.

图5 f0 为2876 Hz 的弯曲波在梯度结构梁中的传播过程Fig.5 Propagation of flexural waves with center frequency f0 of 2876 Hz in beam with graded pillars
在f0为2876 Hz 的时域仿真结果中,提取了梁中如图6(a)所示的4 个点处的正应变时间历程.由于反射,点1、点2 和点3 的时间历程中都有两个波包,如图6(b)所示,绿框内是入射波,蓝框内是反射波.点4 位于第8 和第9 个立柱中间,此处是2876 Hz的弯曲波停止向前传播的位置.在此处入射波和反射波完全叠加成了一个波包.所以入射波和反射波的叠加是产生波场能量增强现象的一个重要原因.然而,入射波波包的最大峰峰值为3.68,反射波波包的最大峰峰值为2.29.点4 处叠加波的最大峰峰值为7.80,为点1 处入射波和反射波波包的最大峰峰值之和的1.31 倍.这说明弯曲波彩虹捕获效应的波场能量增强现象并不只是由入射波和反射波的叠加导致的.弯曲波在点4 处群速度的减小使得弯曲波能量在此处产生了累积,如前面机理分析部分阐述,这是产生波场能量增强现象的另一个重要原因.
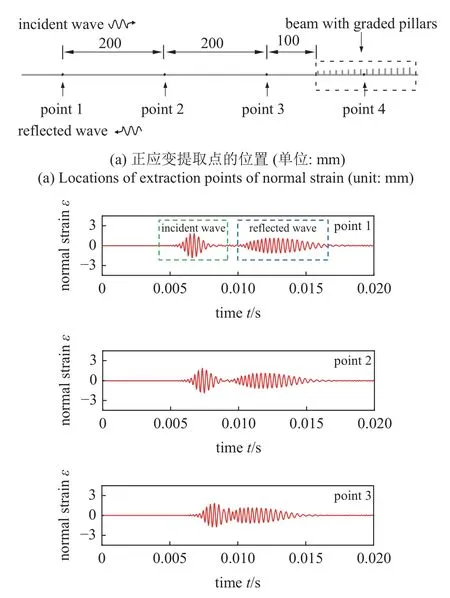
图6 波场能量增强现象的产生机理验证Fig.6 Generation mechanism of wave field energy enhancement
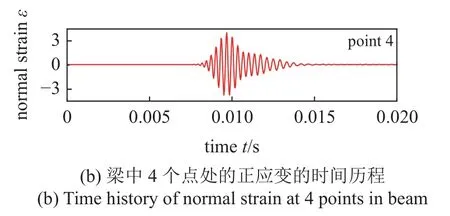
图6 波场能量增强现象的产生机理验证(续)Fig.6 Generation mechanism of wave field energy enhancement (continued)
2.2 彩虹捕获效应实验
本文实验中所用的实验件如图7(a)所示.在实验件两端粘贴蓝丁胶吸收弯曲波,避免其在边界产生反射.使用的仪器为激光多普勒测振系统PSV400和功率放大器HVPA05.图7(b)展示了实验设备.具有相应频率的激励信号由电脑产生,经过功率放大器后传给粘贴在实验件上的压电片(在后面的图和正文中用PZT 表示)来产生相应频率的弯曲波.用PSV400 的激光头扫描实验件背面各点,以获得弯曲波在实验件中的传播情况.在实验中,PZT 激励频率与频域仿真频率保持一致.

图7 弯曲波彩虹捕获效应实验设置Fig.7 Experiment setting for rainbow trapping of flexural waves
PSV400 可测量的物理量只包括位移和速度,无法测量实验件中的应变分布.本文通过材料力学[31]中的相关知识对实验测得的基梁表面的挠度数据进行处理,来间接得到基梁表面正应变的分布情况.梁在发生小挠度弯曲时,梁表面正应变与挠度之间的关系为

式中,z0为梁表面到中性层的距离.
图8(a)展示了基梁表面挠度的频域实验云图.图8(b)是根据式(19)对图8(a)中的数据进行二阶数值微分后得到的基梁表面正应变云图.与图4 相比,图8 在1906 Hz 时第10 个元胞附近,3070 Hz,3771 Hz,4352 Hz 时最右端附近也有波场能量增强现象.这是实验数据误差和数据处理方法共同导致的假象,而非物理上真实的波场能量增强现象——受实验环境的影响,在这几个位置测得的挠度大于其周围位置,进而又导致此处挠度的二阶数值微分也大于其周围位置.除此之外,实验结果可以验证弯曲波彩虹捕获效应的空间分频现象和波场能量增强现象.
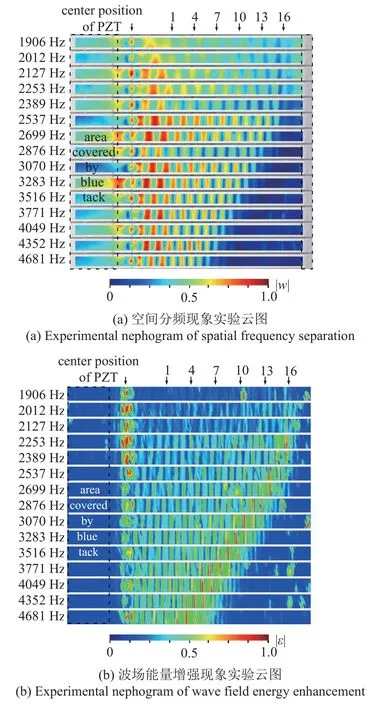
图8 弯曲波彩虹捕获效应实验结果Fig.8 Experimental results of rainbow trapping of flexural waves
3 基于彩虹捕获效应的压电能量俘获
3.1 有限元仿真
本部分将利用弯曲波彩虹捕获效应的波场能量增强现象进行压电能量俘获研究.如图9(a)所示,将每两个立柱之间的基梁部分作为一个单元,定量评估梯度结构梁相对于均匀梁的能量俘获效果及其随入射波频率的变化规律.通过COMSOL 进行的固体力学-压电-电路多物理场耦合仿真示意图如图9(b)所示.压电材料使用COMSOL 材料库压电模块中的PVDF,其厚度设置为0.11 mm.将外接电路中的电阻R设1×108Ω,其两端的电压可以认为是PVDF 的开路输出电压.使用和分别表示粘贴在梯度结构梁和均匀梁中第n个单元处的PVDF 的输出电压.为了定量比较和的相对大小,定义二者之比为电压比
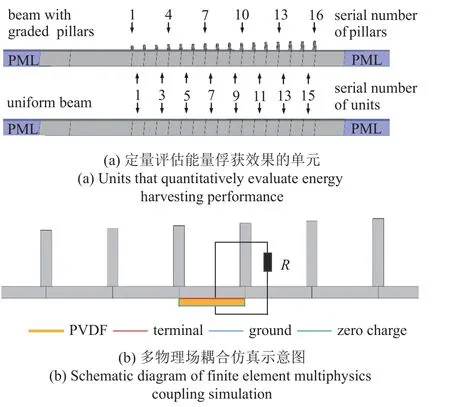
图9 能量俘获有限元仿真模型Fig.9 Finite element simulation model of energy harvesting

图10展示了梯度结构梁相对于均匀梁的第n(n=1,3,…,15)个单元的电压比与弯曲波频率的关系.图中灰色区域代表在第n个单元附近发生彩虹捕获效应的弯曲波频带,其边界为各个元胞的零群速度点频率.由于第n个单元位于第n和第n+1个立柱之间,频率f满足f<fn+1的弯曲波都可以几乎不衰减地传播到此处.此时在立柱的多重散射作用下,入射波和反射波的叠加会导致稍大于1;频率f满足fn+1<f<fn的弯曲波将会在第n个元胞附近发生彩虹捕获效应.此时由于波场能量增强现象,将达到最大值,最大值在2 左右.这说明,发生弯曲波彩虹捕获效应时,梯度结构梁上PVDF 的输出电压约为对应均匀梁的2 倍;频率f满足fn<f的弯曲波在传播到此处之前就会迅速减小,将趋于零.

图10 各单元处电压比与弯曲波频率的关系Fig.10 Relationship between voltage ratio at each unit and flexural wave frequency
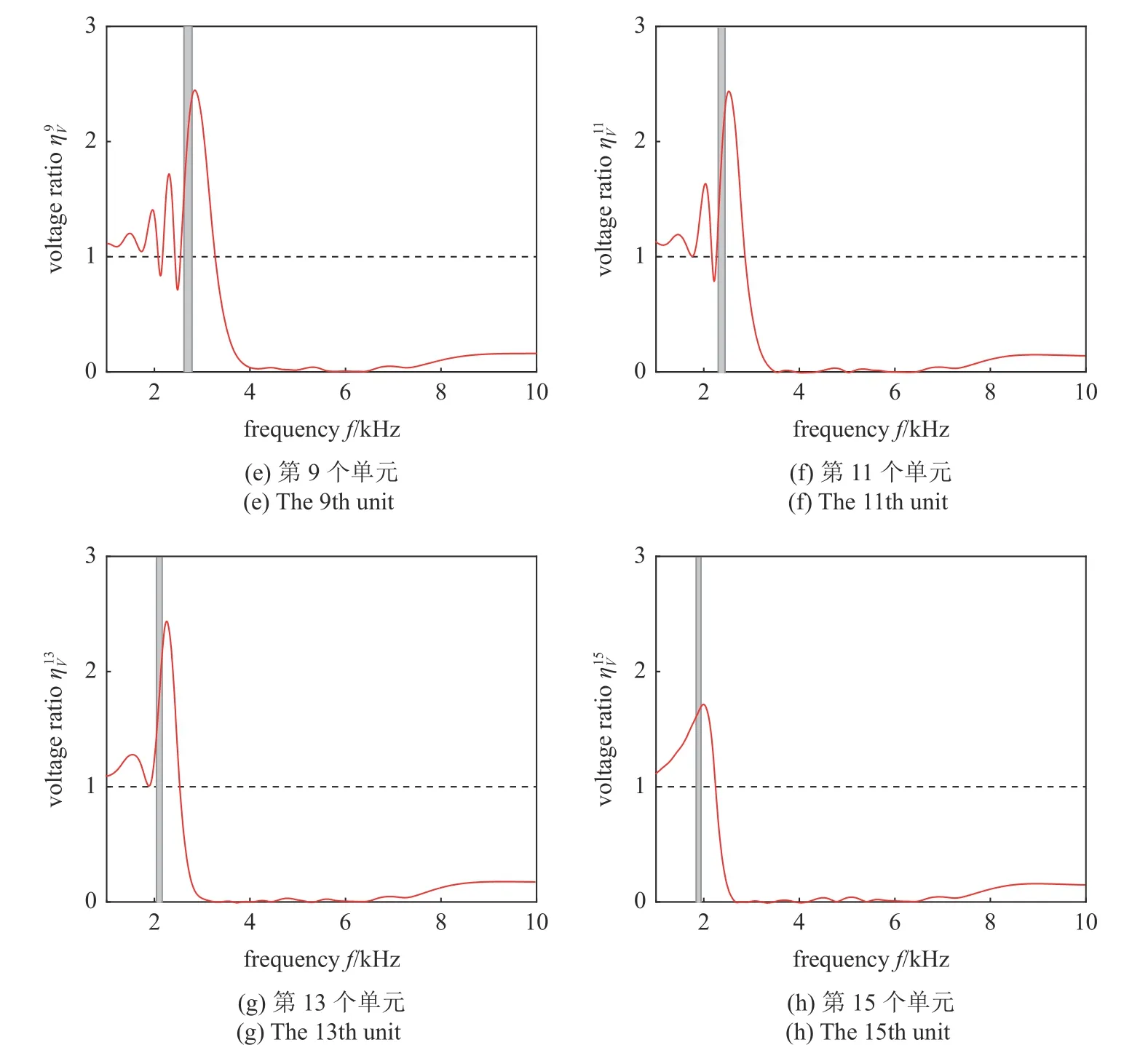
图10 各单元处电压比与弯曲波频率的关系(续)Fig.10 Relationship between voltage ratio at each unit and flexural wave frequency (continued)
3.2 弯曲波能量俘获实验
本文用于弯曲波能量俘获实验的梯度结构梁和均匀梁实验件,以及实验现场如图11 所示.在两个实验件的表面各粘贴三片PVDF,粘贴位置分别对应仿真模型的第1,8 和15 个单元.PVDF 的参数如表2 所示.
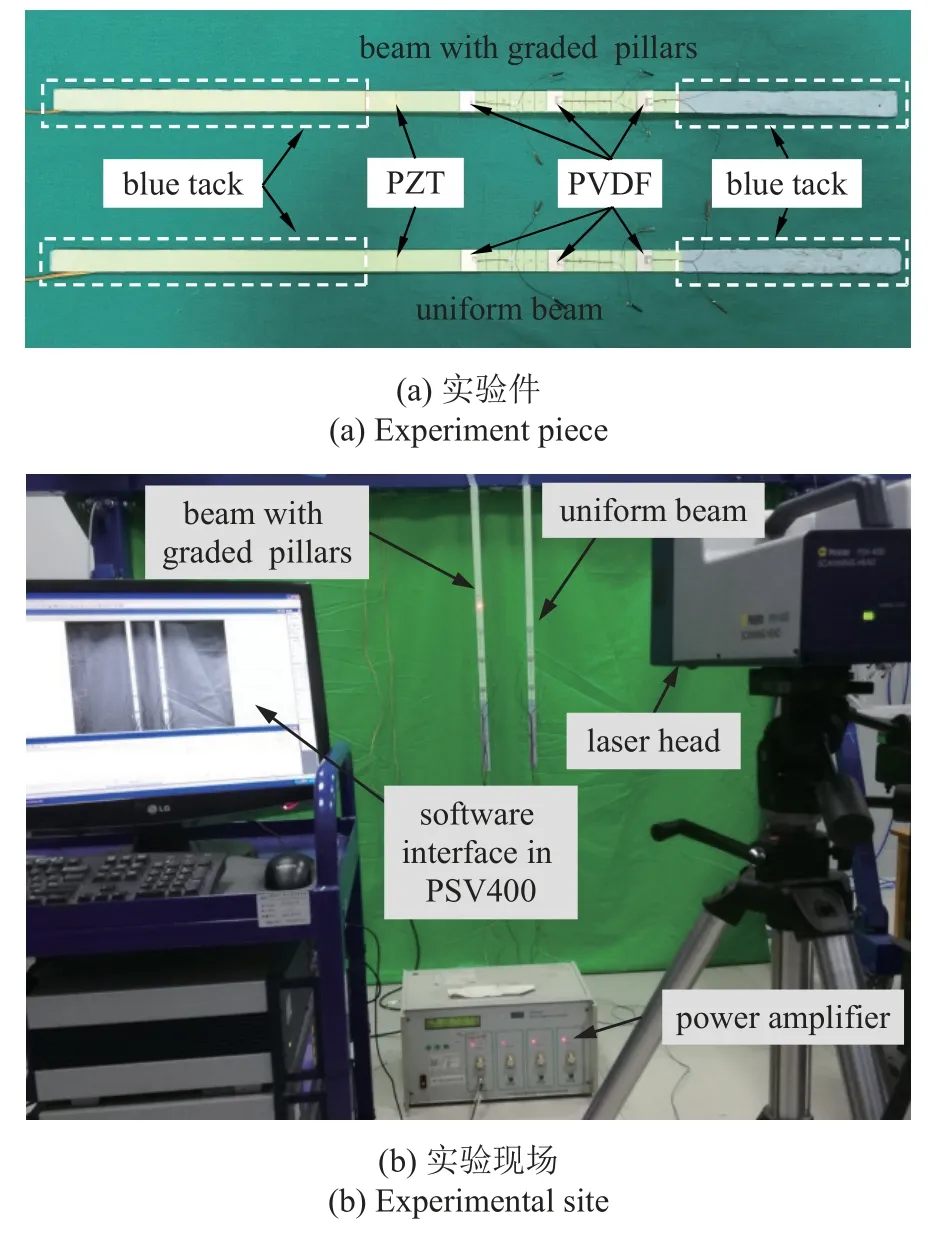
图11 弯曲波能量俘获实验设置Fig.11 Experiment setting for flexural wave energy harvesting

表2 PVDF 的参数Table 2 Parameters of PVDF
在实验中,施加给PZT 的是相同电压幅值的5-cycle tone burst 时域激励信号.图12(a)、图13(a)和图14(a) 分别展示了在f0为4681 Hz,2876 Hz 和1906 Hz 的时域信号激励下梯度结构梁和均匀梁PZT 激励点处的位移.图中标出了位移的最大峰峰值.可以看出,给不同的PZT 施加完全相同的电压信号,激发的弯曲波强度会有差异: 梯度结构梁上的PZT 产生的弯曲波比均匀梁上的PZT 产生的弯曲波要弱.这是制造工艺的限制所导致的.
由前面的分析可知,PZT 产生的三束弯曲波将分别在第1、第8 和第15 个单元处停止向前传播并产生波场能量增强现象.图12(b)展示了粘贴在第1 个单元处的PVDF 在f0为4681 Hz 的弯曲波激励下的输出电压.图13(b)展示了粘贴在第8 个单元处的PVDF 在f0为2876 Hz 的弯曲波激励下的输出电压.图14(b)展示了粘贴在第15 个单元处的PVDF在f0为1906 Hz 的弯曲波激励下的输出电压.图中标出了输出电压的最大峰峰值.通过对比可知,尽管梯度结构梁中的弯曲波强度比均匀梁中的弱,但是粘贴在前者表面的PVDF 的输出电压仍然更高.

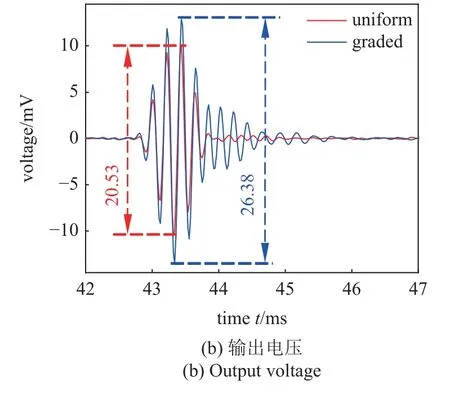
图12 f0 为4681 Hz 的弯曲波在第1 个单元处的能量俘获实验Fig.12 Energy harvesting from flexural wave with center frequency of 4681 Hz at the 1st unit
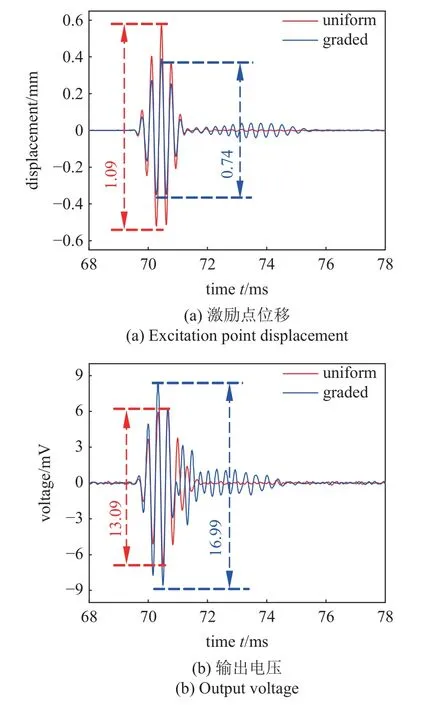
图13 f0 为2253 Hz 的弯曲波在第8 个单元处的能量俘获实验Fig.13 Energy harvesting from flexural wave with center frequency of 2253 Hz at the 8th unit
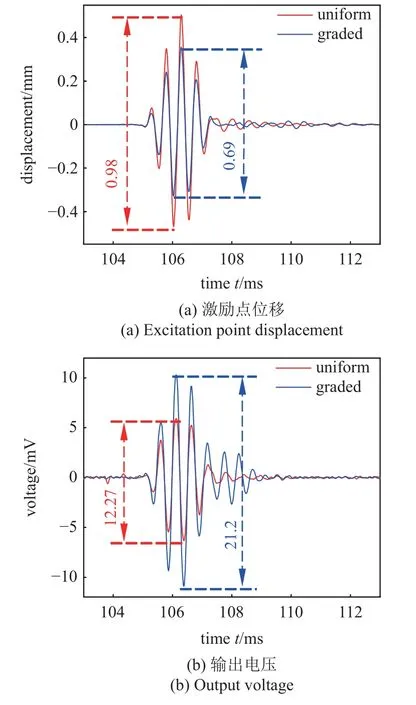
图14 f0 为1906 Hz 的弯曲波在第15 个单元处的能量俘获实验Fig.14 Energy harvesting from flexural wave with center frequency of 1906 Hz at the 15th unit
为了定量比较梯度结构梁相对于均匀梁的俘能优势,本文用输出电压的最大峰峰值除以对应激励点位移的最大峰峰值,将输出电压进行归一化处理.表3 展示了梯度结构梁与均匀梁俘能效果,粘贴在梯度结构梁上的PVDF 的归一化电压输出率约为均匀梁对应位置处的2 倍.这与前面通过仿真得到的结论一致.

表3 梯度结构梁与均匀梁俘能效果Table 3 Energy harvesting performance of beam with graded pillars and uniform beam
4 结论
本文通过所设计的梯度结构梁,系统地研究了弯曲波彩虹捕获效应及其在压电能量俘获中的应用.首先,利用梯度结构梁元胞能带结构的解析解,分析了弯曲波彩虹捕获效应的产生机理: 不同频率的弯曲波在不同的元胞附近达到零群速度后被反射,导致了空间分频现象;弯曲波群速度的减小使得弯曲波能量在相应的元胞附近产生累积,以及入射波和反射波的叠加,导致了波场能量增强现象.其次,通过有限元仿真和实验验证了弯曲波彩虹捕获效应的空间分频现象和波场能量增强现象.最后,通过有限元多物理场耦合仿真和实验,研究了粘贴PVDF压电薄膜的梯度结构梁相对于均匀梁的弯曲波能量俘获效果.结果表明,在弯曲波彩虹捕获效应发生频带内,梯度结构梁上的PVDF 压电薄膜的输出电压约为均匀梁相应位置处PVDF 压电薄膜的输出电压的2 倍.在未来的工作中,对彩虹捕获效应的研究将从物理现象和工程应用两个方面开展.对于前者,将探索梯度结构中弯曲波模式和纵波模式耦合的彩虹捕获效应.对于后者,将利用彩虹捕获结构进行基于空间分频现象的弹性波滤波器的研发,以及基于波场能量增强现象的工程结构减振、弯曲波吸收和声辐射抑制研究.
数据可用性声明
支撑本研究的科学数据已在中国科学院科学数据银行ScienceDB 平台公开发布,访问地址为http://doi.org/10.57760/sciencedb.j00140.00001或http://cstr.cn/31253.11.sciencedb.j00140.00001.
附录
传递矩阵的具体形式如下