基于SHAP-RF 框架的越野车辆路面识别算法研究1)

赵 健 刘彦辰 朱 冰 李 扬 李雅欣 孔德成 姜泓屹

(吉林大学汽车仿真与控制国家重点实验室,长春 130022)

引言

尽管随着经济科技水平的发展,城市和乡村的路面铺装率都得到了提升[1],但非结构化道路依然大量存在,一些特殊任务例如野外救援、军事运输等都需要车辆在非结构化道路上有良好的行驶性能[2].在结构化道路上,路面平整、附着良好,路面环境相对单一而稳定,车辆能够顺利行驶;而在越野环境中,路面情况复杂多变,不同类别路面的软硬程度、附着条件、材质都具有明显的不同,如果车辆能够感知到当前所处路面的状态,就能对底盘各控制子系统参数进行适当的调整,以获得更好的通过性、平顺性与操纵稳定性等[3-8].

路面类型识别方法大体可以分为基于视觉的识别[9-11]与基于车辆动力学特征[12-13]的识别两大类,此外还有基于图像和车辆动力学信息的多传感器融合识别方法[14-17].对基于车辆动力学特征的识别方法而言,路面识别结果不会受到光照等外界复杂环境因素影响,同时由于分类模型本身就隐含了车辆与路面的相互作用机理,其识别结果对车辆控制也更具有应用价值;而多传感器融合的方法虽然能够在考虑前方路面的纹理和颜色信息的同时,兼顾车轮与地面间的相互作用机理,但受限于多传感器融合方法的“木桶效应”,车辆动力学方法的识别精度仍然对融合精度有较大影响.

但是越野路面特征复杂多变,而车辆与不同类型的路面的作用机理难以准确描述,因此近年来学者们开始采用数据驱动的方法,利用机器学习算法对非线性问题进行拟合.Brooks 等[18]采集了车轮的振动信号,然后从频域的角度对信号分析并提取出了车轮振动的功率谱密度特征,利用线性判别分析法实现了土路与沙地等路面的识别.Sadhukhan等[19]搭建了包括惯性导航系统、声呐系统与轮速编码器的车辆行驶数据采集平台,以车辆驶过由4 种路面组成的混合路面时的垂向加速度信号作为基础,提取信号的频域特征,并将这些特征输入到神经网络中,实现了路面的识别.杨帆等[20-21]采集了试验车在不同路面下行驶时车轮垂向力的信号,并对信号进行特征提取,利用支持向量机实现路面的分类.薛开等[22]在车轮架上安装了传声器和加速度计,采集车辆在各种路面上的振动信号,基于k-近邻法实现了路面的分类.武维祥[23]通过从车辆CAN 总线得到的信号估计车辆的轮速波动量与滚动阻力,然后以轮速波动量与滚动阻力作为输入,分别采用模糊规则与随机森林完成了软路面的识别.

虽然上述基于机器学习的路面分类模型表现优秀,但其结构复杂的特点使得人们难以清晰理解模型做出决策的过程,人们一般把这些模型当作“黑盒”来处理[24],也就难以理解模型输入对输出的作用机制,若能对黑盒的路面分类模型加以解释,并针对模型解释结果对分类模型加以改进,可以使模型更加易于理解,提升模型的可靠性,实现路面类型的准确识别.在机器学习中,可解释性定义为对模型内部机制的理解以及对模型输出结果的理解[25].Zeiler等[26]提出了一种新颖的CNN 隐层可视化技术,从信息提供性方面入手,通过特征可视化查看精度变化,将隐层转化成人类可以理解的有实际含义的图像,从而了解CNN 学习到怎样的特征.Hinton 等[27]提出了一种知识蒸馏方法,通过训练单一的相对较小的网络来模拟原始复杂网络或集成网络模型的预测概率来提炼复杂网络的知识,并且证明单一网络能达到与复杂网络几乎同样的性能.Lundberg 等[28]将博弈论与模型解释联系起来,提出了SHAP(Shapley additive explanation)解释法,该方法是构建一个线性可加模型并将特征归因化,通过SHAP值来反应出一个特征对模型输出的影响的大小.Khaleel 等[29]提出一种文本解释性的伪真值生成方法,并以之为基准对6 种模型解释方法进行评价,最终表明(layer-wise relevance propagation,LRP)对深度文本分类器的解释性能更佳.全文君[24]提出了一种基于标准化数据挖掘过程(CRISP-DM)的可解释性研究框架与一种原始数据理解流程,并结合认知理论,提出了一种基于人分类学习的黑盒模型解释法(HCLI).杨晔民等[30]设计了可视分析系统FORESTVis,这套分析系统包括多个可视化组件,利用该系统可以直观地了解随机森林的结构特点和工作流程与机理,并对人们评估模型的性能提供了便利.

针对目前基于车辆动力学特征的路面识别方法存在的输入特征过多、可解释性不足的问题,本文从模型解释的角度提出SHAP-RF 路面识别算法设计框架.采集车辆在压实土路、沙地、良好沥青路与冰雪路上的行驶数据,并设计3 个次级行驶特征特征的计算方法,进而进行信号的时域和频域统计特征计算;基于全部特征建立高维随机森林路面识别模型,采用SHAP-RF 路面识别算法设计框架,解释分析高维模型中输入特征对分类结果的影响并进行有效的特征筛选,据此重新构建基于随机森林的降维路面分类模型,以期在使用较少分类特征的情况下保证车辆行驶路面类别的有效识别.

1 数据采集和特征计算

1.1 车辆行驶数据采集

采用图1 所示的数据采集系统,试验车上安装了RT3000 惯导系统、罗技Pro-C920 高清摄像头、CAN 总线收发分析工具VN1630 A 和上位机.其中,试验车为某款全尺寸SUV,搭载丰富的传感器与电控系统,通过CAN 总线与VN1630 A 进行信号传输;RT3000 惯导系统用于车辆运动数据的采集与对照;摄像头对车辆行驶过程进行记录,为后续的数据标记与处理提供便利.

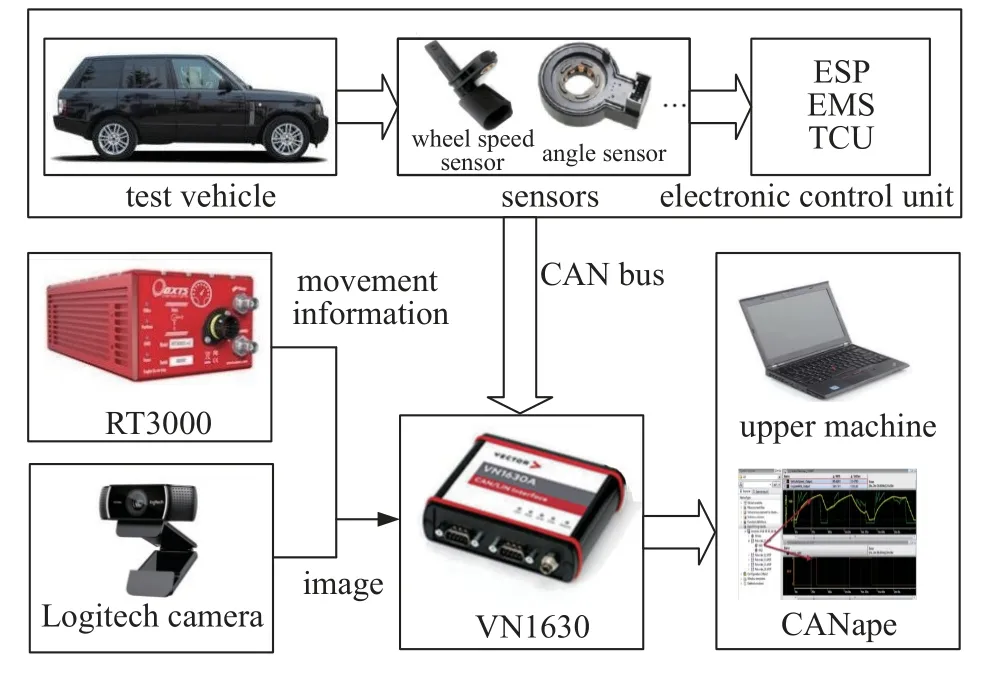
图1 数据采集系统示意图Fig.1 Data acquisition system

图2 4 种典型路面Fig.2 Four typical road surfaces

数据采集系统采集的主要信号如表1 所示.本文所设计的算法需要识别压实土路、沙地、良好沥青路与冰雪路4 种典型路面,如图2 所示,在保证通过性的情况下,对4 种路面分别选取试验工况进行数据采集,为避免偶然因素造成数据集的污染,每种工况下都尽可能进行多次试验以保证获取足够的有效数据.

表1 采集的主要信号Table 1 Part of the collected signal

1.2 次级行驶特征计算

数据采集系统直接采集的每一种原始数据所体现的车辆在不同路面上行驶特征的直观性不强,且各个原始数据之间也存在一定程度的耦合,因而有必要进行次级行驶特征的计算.本文考虑到算法识别的路面类别中存在软硬程度和路面轮廓的差异,对车辆行驶阻力和车身振动会产生不同程度的影响,因此设计了车辆滚动阻力Ff、轮速波动量Δ和垂向加速度系数acoe3 个次级行驶特征的计算方法.

1.2.1 车辆滚动阻力Ff

汽车在不同路面行驶时受到的道路阻力有明显差别,在沙地等松软土壤上行驶时的道路阻力远大于硬路面,这一阻力可以作为路面识别的重要依据.

在车辆直线行驶时,受到的阻力由加速阻力、坡度阻力、空气阻力和滚动阻力4 部分构成[31],车辆的纵向受力如图3 所示.

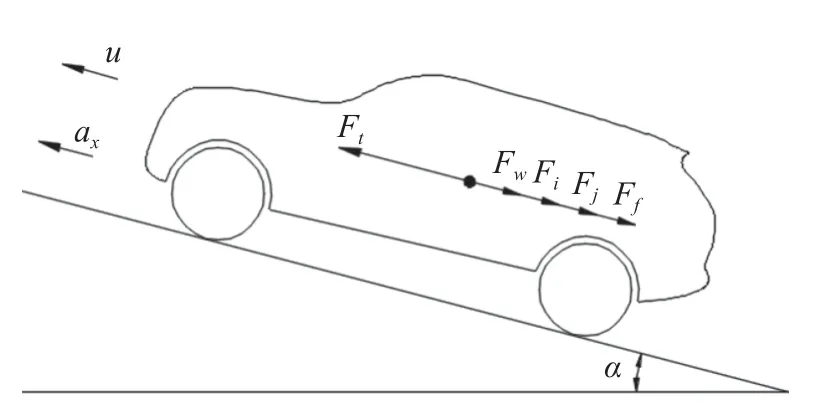
图3 车辆纵向受力示意图Fig.3 Diagram of longitudinal force on vehicle

根据车辆的受力情况,可以得到驱动力-行驶阻力平衡方程

式中,Ft为发动机输出的扭矩传递到车轮后所产生的驱动力,Ff为车轮在路面滚动时产生的阻力,Fw为空气作用于车身上产生的空气阻力,Fj为在加速时克服惯性产生的加速阻力.

根据式(1),可计算车辆的滚动阻力为

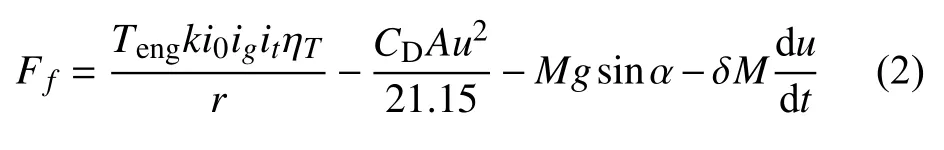
式中,Teng为发动机输出的扭矩,可以通过发动机的EMS 系统获取,k为液力变矩器的变矩系数,i0为主减速器的传动比,ig为变速器的传动比,it为分动器的传动比,ηT为整个传动系统的传动效率,其大小会随着液力变矩器的速比发生变化,r为车轮的滚动半径;CD为汽车的风阻系数,A为汽车在正面的投影面积的大小,u为车辆的行驶速度;M为整车的质量,α为道路的坡度角;δ为旋转质量换算系数.

由于车辆的平动加速阻力和坡度阻力理论上并不相关,而车辆搭载的加速度传感器测量车辆行驶方向的加速度时会将两者耦合,即

因此为了计算方便,将滚动阻力的计算公式转换为以下形式

式中，ax_car为车辆搭载的加速度传感器测量的车辆行驶方向的加速度.

此外,为了消除滚动阻力的抖动,真实地反映道路的滚动阻力,对滚动阻力Ff进行滤波处理,得到滤波后的滚动阻力Ff_flt,计算良好沥青路面上的如图4 所示.

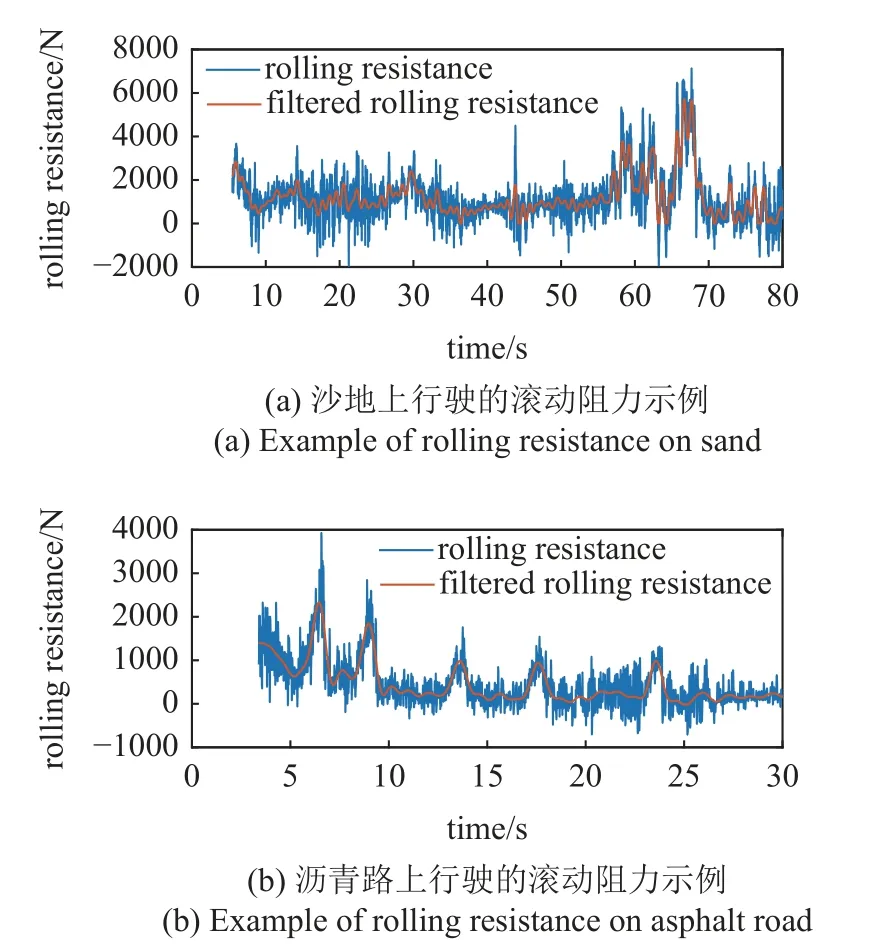
图4 滚动阻力计算结果示例Fig.4 Example of rolling resistance

1.2.2 轮速波动量Δ

当车辆行驶在各种不平整的地面上时,轮速会产生较大波动,而当车辆在沙地或附着系数比较小的路面上行驶时,由于土壤的表层破坏或者车轮到达附着极限,车轮也会抖动甚至是打滑,如图5 所示.因此将四个车轮的轮速波动量作为识别的依据.

在计算轮速波动量时,还需要考虑车辆转向造成的左右侧车轮轮速差异,如图5 中局部放大部分所示,为消除这种轮速差异,采用图6 所示的阿克曼转向几何模型对轮速进行修正.

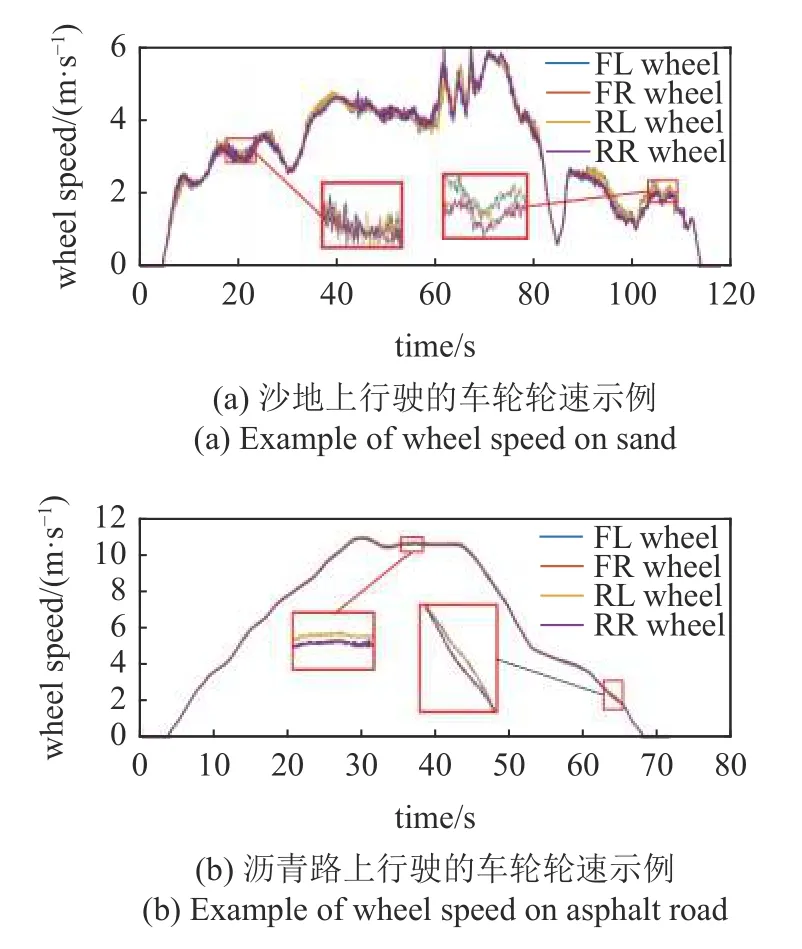
图5 不同路面上的车轮轮速示例Fig.5 Example of wheel speed on different road

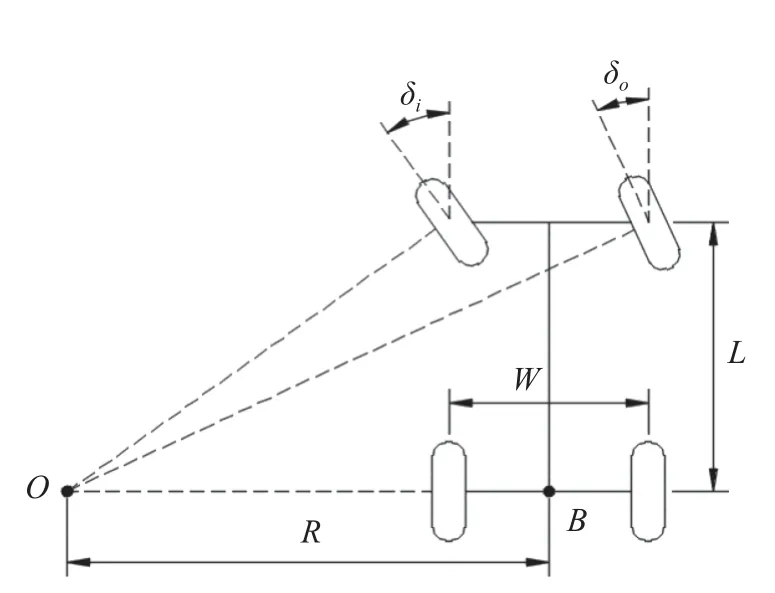
图6 阿克曼转向几何模型Fig.6 Ackermann steering geometry

将每个车轮的轮速转换成车辆后轴中心B点处的速度

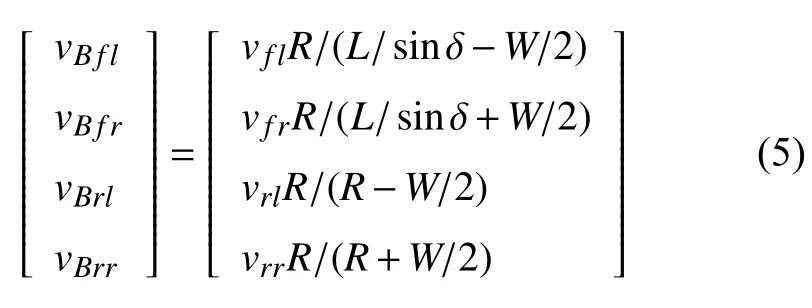
式中vBfl,vBfr,vBrl,vBrr分别为汽车的左前轮、右前轮、左后轮、右后轮轮速等效至车辆后轴中心处的值,vfl,vfr,vrl,vrr分别为汽车的左前轮、右前轮、左后轮、右后轮的轮速,R为汽车后轴中心B点处对应的转弯半径,W为轮距,L为轴距,δ为车轮的转向角,忽略内外侧车轮转向角差异.

定义轮速波动量计算式为

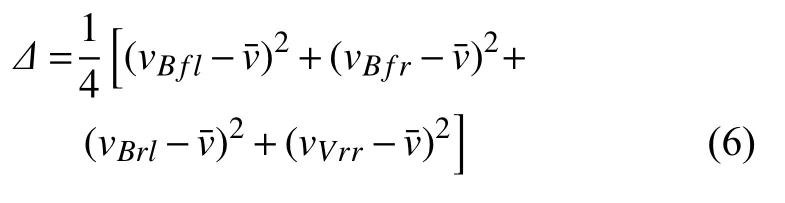
图7 不同路面上的轮速波动量示例Fig.7 Example of wheel speed fluctuation on different road surfaces

1.2.3 垂向加速度系数acoe

路面在垂直方向上的高度变化是路面振动激励的主要成分,路面轮廓输入可以用傅里叶级数表示为无数个正弦波的叠加形式[32],即

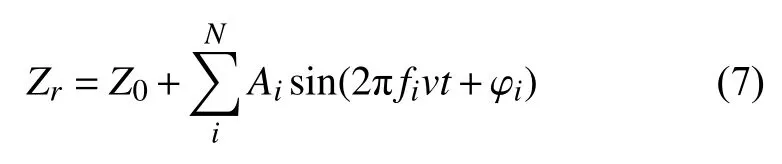
式中，Zr是地面轮廓的高度,fi是空间频率,Ai和φi是空间频率为fi的正弦波分量的幅值和相位偏移,v是行驶速度,t为时间.

将式(7)对时间t进行两次微分后可以得到

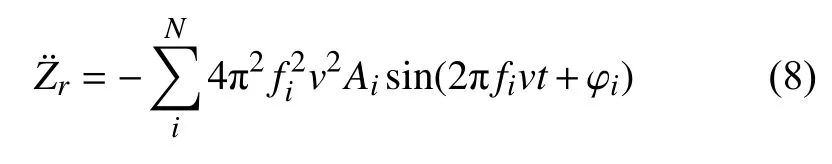
由式(8)可知,路面激励下车辆垂向加速度响应受到车辆行驶速度的影响,本文定义一个新的特征垂向加速度系数acoe来消除车速对车辆垂向加速度的影响,acoe定义式为

式中，az为车身的垂向加速度,n为一个常数,在同一种路面下n的取值应当使acoe的波动程度与车速的相关程度最小,n的取值通过试验数据计算获得.良好沥青路面上车辆行驶数据共46 段,每段数据长度不小于30 s,包括车速范围2～ 100 km/h,采用如下步骤获取n的值:

(1)将各数据段中的垂向加速度数据不重叠地划分成每128 帧一组;

(2)对n的不同取值,计算每组数据中垂向加速度系数标准差σacoe与车速的均值vmean;

(3)计算n的不同取值下,σacoe与vmean的相关系数,相关系数最接近0 时,acoe的波动程度与车速的相关性最小,此时n的值作为最终取值.

σacoe与vmean的相关系数随n值变化曲线如图8所示,最终取n=0.4,并计算垂向加速度系数示例如图9 所示,可以看出与垂向加速度相比,其波动程度与车速的相关性明显减小.

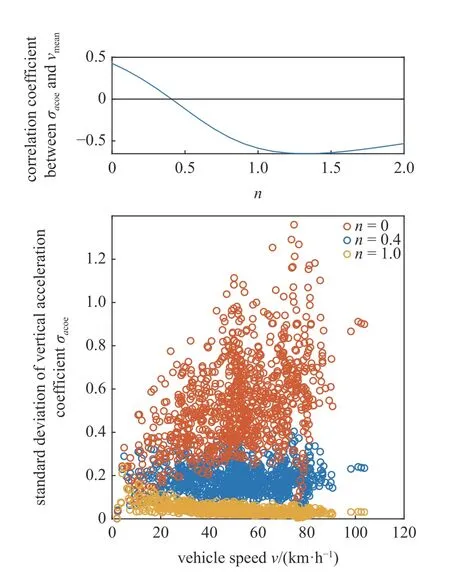
图8 相关系数随n值变化情况Fig.8 Correlation coefficients with different nvalues

图9 垂向加速度系数计算示例Fig.9 Example of vertical acceleration coefficient

2 SHAP-RF 路面识别算法设计框架

2.1 架构设计

基于机器学习算法设计路面分类器,特征选择的合理性对算法的分类效果有决定性的影响.通常情况下,基于数据的时域和频域统计计算可以获得大量特征.然而使用大量特征会增加机器学习算法的复杂度,容易导致过拟合现象,分类模型的泛化能力变差,因此需要对数据特征进行降维.本文所设计的SHAP-RF 路面识别算法框架,采用RF 方法设计路面分类器,并用SHAP 模型解释方法实现降维操作.相比常用的数据降维方法,例如主成分分析(principal component analysis,PCA) 和因子分析(factor analysis,FA),采用的SHAP 模型解释方法不对特征进行变换,同时能够获得特征的重要性和对路面类别输出的影响情况,从而为高维RF 模型的降维提供指导.

本文所设计的SHAP-RF 路面识别算法框架如图10 所示.首先进行数据的时域和频域统计特征计算,获得大量待筛选特征;随后采用随机森林算法设计了一个采用全部待筛选特征的高维路面识别模型,基于SHAP 解释法对高维模型进行解释,分析各特征对准确识别结果的贡献度和依赖度;以此为基础缩减高维模型的输入特征维度,完成降维随机森林路面识别模型的设计.

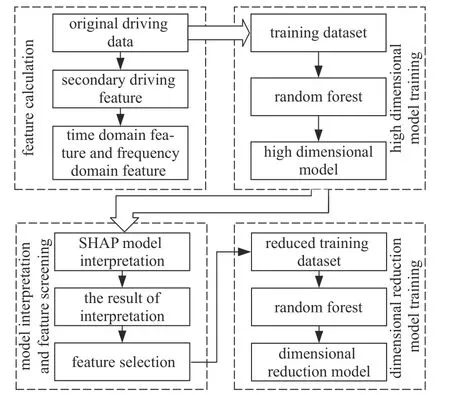
图10 SHAP-RF 路面识别算法设计框架Fig.10 SHAP-RF road identification algorithm design framework

2.2 时域特征和频域特征计算

除了行驶特征本身的数值以外,行驶特征在一段时间内的波动情况也与路面类型有关,因此对行驶特征数据进行时域特征与频域特征的提取,包括四轮轮速vfl,vfr,vrl,vrr,车身垂向加速度az和3 个次级行驶特征Ff,Δ和acoe.其中,4 个车轮的轮速在时间上的变化受到车辆加速与减速动作的影响,因此只对4 个车轮轮速的频域特征进行提取,不提取时域特征.具体步骤如下.

(1)行驶条件判断: 由于车辆速度较小的时候,受信号采集精度限制,行驶特征参数变化异常,因此进行特征计算时,只对车速大于2 km/h 的数据进行计算.

(2)采用线性插值的方法,将传感器数据的采样频率进行同步.

(3)提取包括当前时刻在内的长度为128 的时间序列信号.

(4)提取时间序列信号的时域特征和频域特征.

最后,获得由行驶特征原始值(包括车身垂向加速度az和3 个次级行驶特征Ff,Δ和acoe)、行驶特征滤波值(滤波后的滚动阻力Ff_flt)以及行驶特征时域特征和频域特征组成的共105 个路面识别特征,如表2 所示.

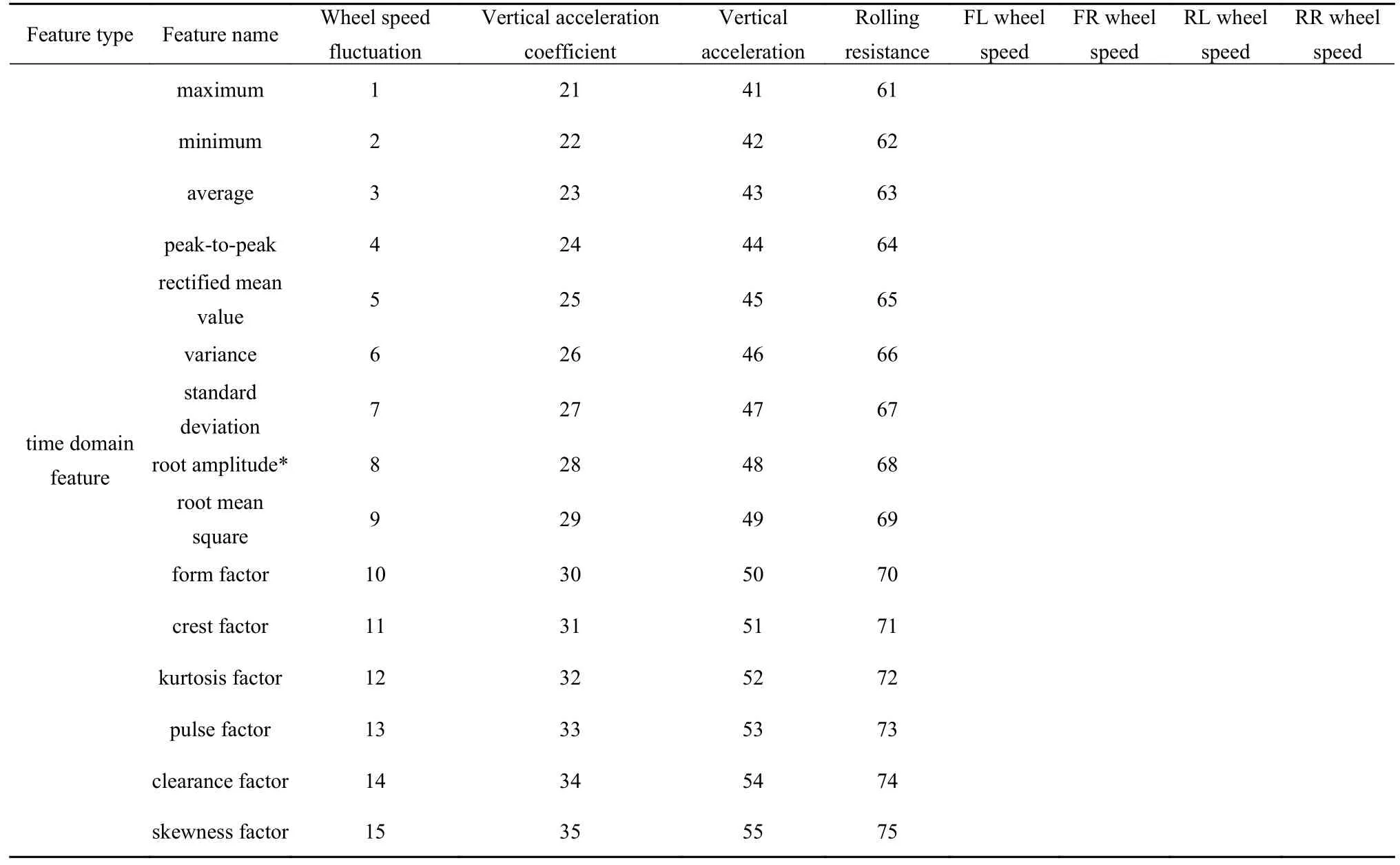
表2 特征编号列表Table 2 List of feature numbers

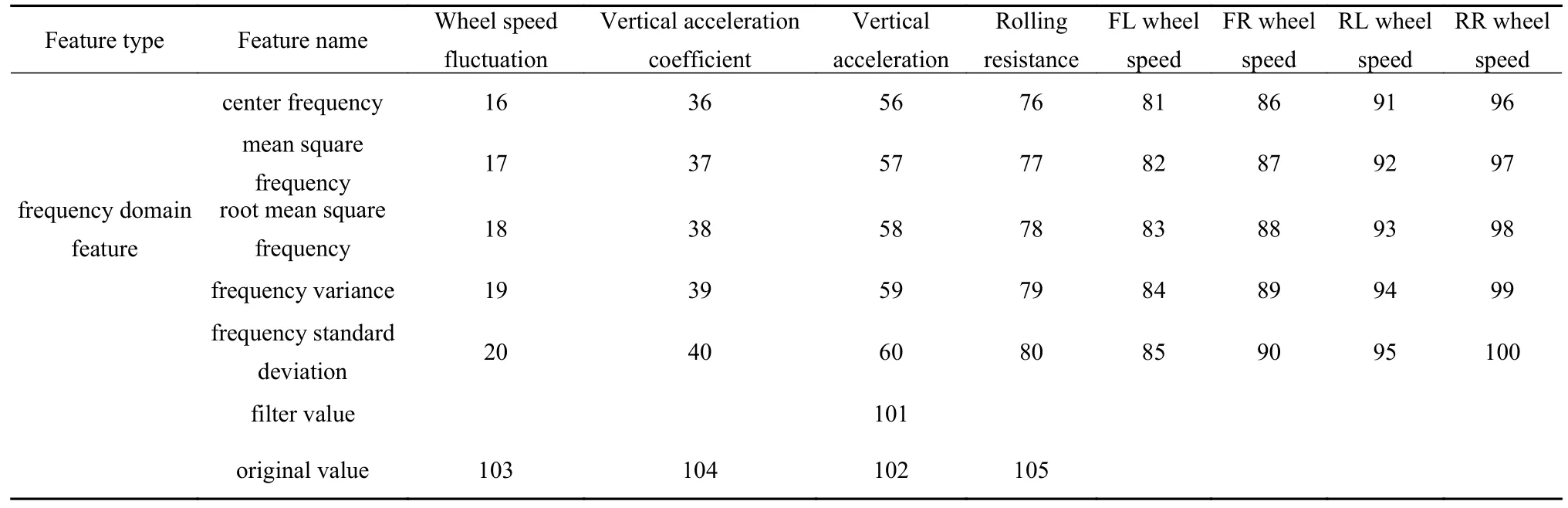
续表 2

2.3 基于SHAP 解释法的模型改进

2.3.1 高维随机森林路面识别模型设计

随机森林(RF)是基于决策树的集成模型,通过随机森林可以实现多种路面识别,相比更加复杂的机器学习算法,其结构相对简单,模型解释的难度与计算量低.本文基于随机森林算法构建路面识别模型,采用105 个特征进行高维路面识别模型训练,选取决策树棵数为100,信息纯度计算标准为gini,对树的生长不做限制,随机森林算法的流程图如图11所示.

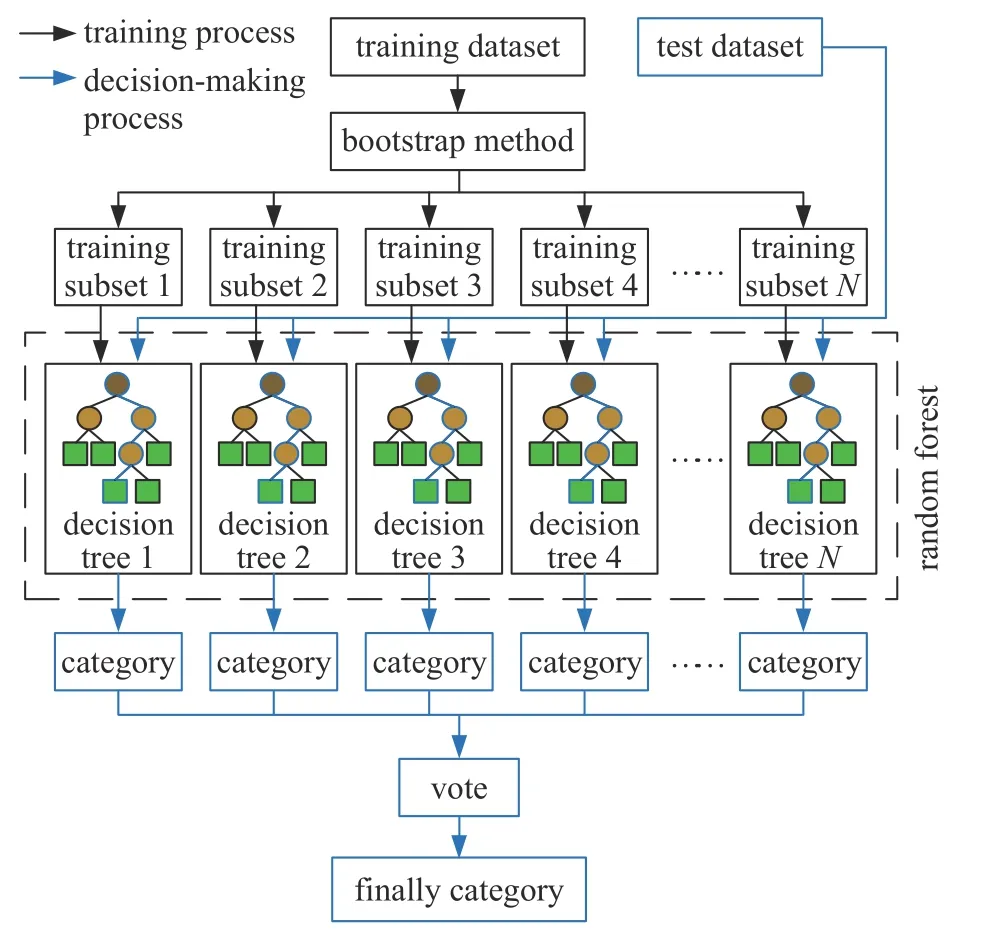
图11 随机森林算法流程图Fig.11 Flow chart of random forest algorithm

2.3.2 基于SHAP 解释法的特征筛选

SHAP 解释法参考合作博弈的分析方法,特征筛选步骤如下.

(1)对所有被解释样本,计算每个特征对路面识别的贡献,即SHAP 值,计算式为

式中,M为特征的个数,F为所有的特征的集合,f为被解释的模型,f(S)=E[f(x) |xS],xi为一个被解释的特征向量实例,为特征向量中的第i个特征,S为F{}的子集,φi为第i个特征的SHAP 值.

(2)统计所有被解释样本的特征的SHAP 值绝对值的均值.

(3)选取对输出贡献较大的特征作为降维路面识别算法的输入.

与基于随机森林算法的高维和降维路面识别模型相对应,采用TreeSHAP,即基于树模型的SHAP 值简化计算方法[33],利用节点走向与节点中样本的比重来计算特征贡献.E[f(x) |xS]的计算流程如图12 所示,图中j为节点索引,dj为在节点j中被利用的特征索引,w为节点的权重,vj为节点取值,aj,bj为节点j的子节点,r为节点中的样本数目.

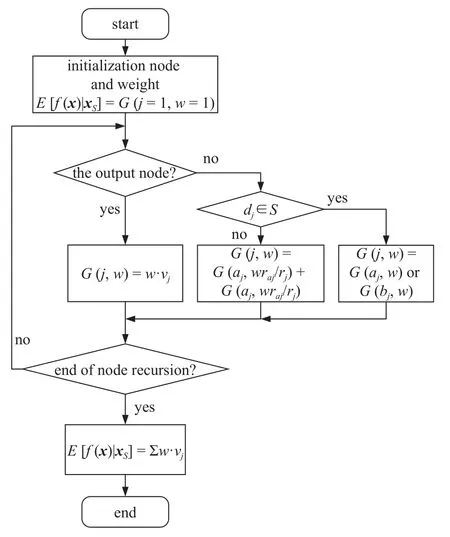
图12 E[f(x) | xS]计算流程Fig.12 Calculation process of E[f(x) | xS]

对全部样本的解释结果如图13 所示,从解释结果来看,车辆的滚动阻力的时域特征(63,61,62,65,69 号特征)对模型输出的贡献最大,轮速波动量的频域信息(18,17,16 号特征)的贡献度次之,垂向加速度系数(29,40,27,25,26,39,21 号特征)与垂向加速度(59,41,60 号特征)的统计信息的贡献相对较小.解释结果可以验证次级行驶特征轮速波动量的有效性,此外,对比发现垂向加速度系数的贡献远比垂向加速度大,再次验证了垂向加速度系数这一特征的有效性.

图13 对全部样本的解释结果Fig.13 Interpretation results for all samples

由于本文研究的分类问题是属于多分类问题,为了更清晰的观察特征对于一类的识别结果的贡献,在指定路面类别下对所有样本的解释结果进行输出,得到的解释结果用散点图表示如图14 所示.以SHAP 值等于0 为分界线,点分布在右侧表示该特征取值会增高对应路面类型的预测概率,反之则会降低对应路面类型的预测概率,增高/降低的程度随SHAP 值绝对值的增大而增大.

图14 指定路面类别的SHAP 解释结果Fig.14 SHAP interpretation results for specific road categories

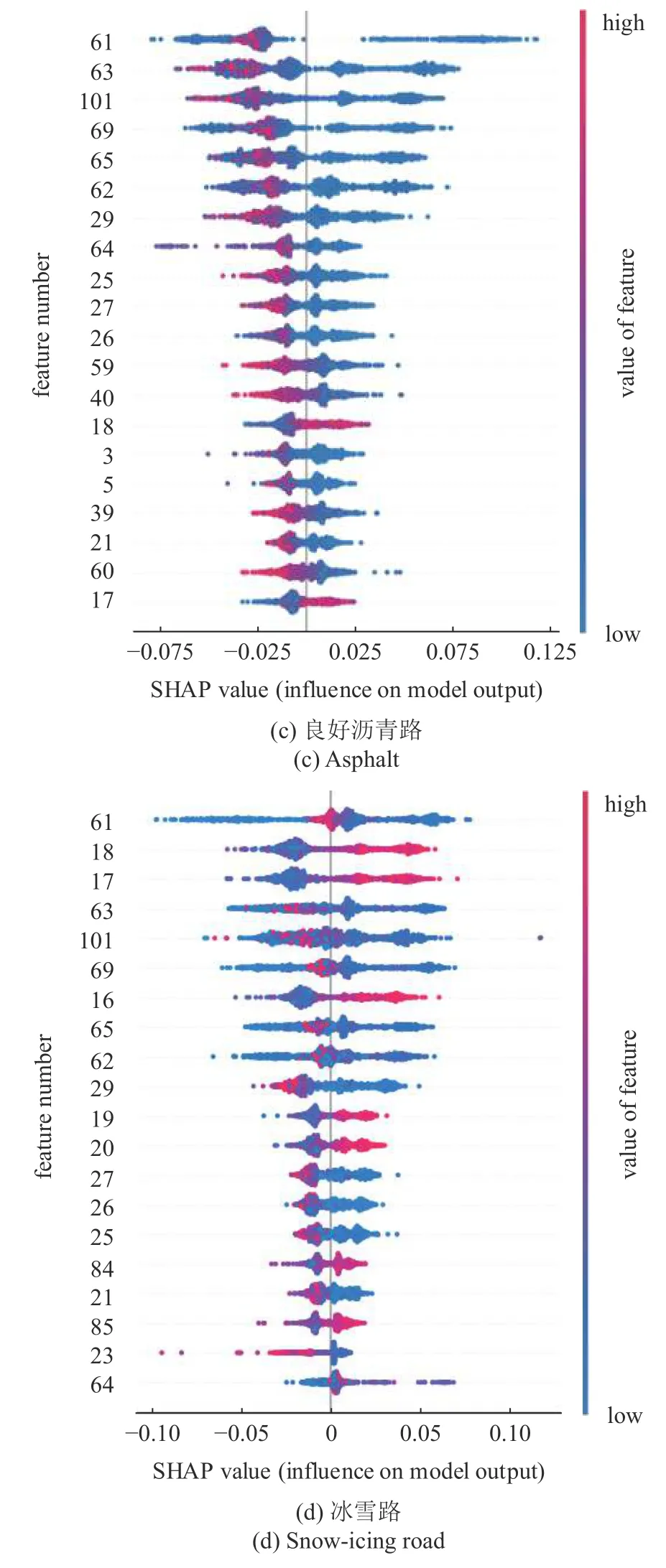
图14 指定路面类别的SHAP 解释结果(续)Fig.14 SHAP interpretation results for specific road categories(continued)

为了探寻特征之间的相互影响,利用SHAP 相互作用指标φi,j来寻找影响因素,φi,j的计算式为

式中i与j为被解释的特征且i≠j,δij的计算式为

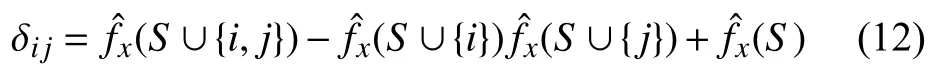
对所有的特征进行 φi,j计算便可以得到一个维度为M×M的矩阵,其中数值最大的数对应的位置代表这两个特征的相互影响最大.

对某一特征进行具体分析，以土路类别识别中29 号特征（加速度系数均方根）的表现为例。图15 为考虑29 号特征与40 号特征（垂向加速度系数频率标准差）相互作用的部分依赖图。从整体上看，29 号特征的SHAP 值随着29 号特征值增大而增大，29 号特征值时小于0.1 时，SHAP 值为负，模型预测结果为土路的概率减小，29 号特征值大于0.1 时则会增大模型预测结果为土路的概率。另一方面，40 号特征的取值也会影响29 号特征的SHAP 值，即影响29 号特征对模型正确分类的贡献。图15 中样本点的颜色表达40 号特征不同数值，偏红表示40 号特征数值较大，偏蓝表示40 号特征数值较小。由图可见，在29 号特征值小于0.08 时，29 号特征的SHAP 值随40 号特征取值的增大而减小，对模型正确分类的负面影响增加，在29 号特征值大于0.08 时，29 号特征的SHAP 值随40 号特征取值的增大而增大，即提高模型正确识别为土路的可能性。

图15 考虑相互作用的部分依赖图Fig.15 Partial dependency diagram that consider interactions

对模型输出影响较大的前20 个特征中，许多特征之间都存在相互作用的关系，在构建路面识别模型时应当对这些特征予以考虑；而对于对模型输出影响不大的特征则进行剔除。本文最终选取对模型整体输出影响排在前20 的特征 (63,61,101,62,65,69,29,18,17,16,40,59,27,25,26,41,39,60,21,3) 作为主要特征，由这些特征组成精简特征向量，作为路面识别的依据。

2.3.3 随机森林路边识别模型改进

以筛选后的20 个特征作为输入,训练降维的随机森林路面识别模型.根据随机森林分类器在测试集上的准确率最高的原则,选取决策树棵数为100,信息纯度计算标准为gini,树的最大深度为13,最小叶节点数为3,进行模型的训练.

3 算法测试与结果分析

从采集的车辆行驶数据中得到20 000 个样本,对压实土路、沙地、良好沥青路和冰雪路4 种路面,每种路面包含的样本数量均为5000 个,对样本集进行随机抽样,抽取10 000 个样本作为训练集,10 000 个样本作为测试集.以精确率和召回率对算法进行评价,其中精确率评价算法的虚报程度,召回率则评价算法的漏报程度.高维路面识别模型在测试集上的分类结果评价如表3 所示.将样本集内不同路面的特征向量输入到降维路面识别模型中,定义压实土路、沙地、良好沥青路与冰雪路对应模型的输出的值分别为1,2,3 和4,得到的输出结果如图16所示.降维路面识别模型在测试集上的分类结果评价如表4 所示.

图16 降维路面识别模型的识别结果Fig.16 Recognition results of dimension reduction road identification model

表3 高维路面识别模型评价Table 3 Evaluation of full-dimension road identification model

表3 中,高维路面识别模型能够达到较高的识别精度,表明其对数据中的信息充分利用,能够支撑后续模型解释的进行,对比表3 和表4,由于特征减少,采用筛选后的特征训练的降维路面识别模型识别精度稍有下降,但下降幅度小,对各种路面的识别精确率和召回率普遍在96%以上,下降幅度相对较大的冰雪路识别精确率和良好沥青路识别召回率的下降幅度也不超过3.2%,即降维路面识别模型依然保持较高的识别精度,表明文本采用的SHAP 模型解释方法能够有效筛选对路面识别有重要作用的特征,本文基于SHAP-RF 框架设计的路面识别算法能够在使用较少分类特征的情况下保证车辆行驶路面类别的有效识别.

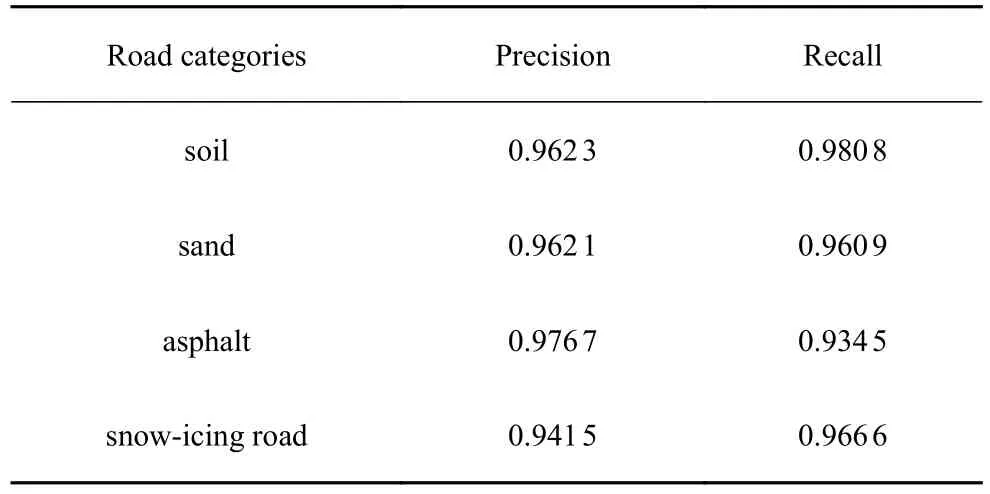
表4 降维路面识别模型评价Table 4 Evaluation of dimension reduction road identification model

对降维路面识别模型再次进行SHAP 解释,得到的解释结果如图17 所示.对比图14 所示的高维模型解释结果,相同的特征在降维路面识别模型与高维路面识别模型中的SHAP 值分布相似,特征的相关性与之前的解释结果基本一致,表明SHAP解释法对特征筛选有效且整体解释较为清晰,再次验证了本文提出的SHAP-RF 框架的有效性.

图17 路面识别模型的SHAP 解释结果Fig.17 SHAP interpretation results of road recognition model

4 总结

提出了一种SHAP-RF 路面识别框架,以实车行驶数据为基础进行特征计算和提取,训练高维路面识别模型,采用SHAP 解释法对高维路面识别模型进行解释,获取特征对模型预测结果的贡献及影响,然后根据特征对模型影响的大小进行特征筛选,形成精简特征向量,基于随机森林算法训练降维路面识别模型,通过仿真和数据回放测试验证了算法的有效性,最终的结果表明:

(1)采用的次级行驶特征: 滚动阻力、轮速波动量和垂向加速度系数在的随机森林路面识别模型中起到重要作用,表明这3 个特征与路面类别间的强大关联性,同时也证明了提出的轮速波动量和垂向加速度系数的有效性.

(2)设计的SHAP-RF 路面识别算法设计框架,能够在使用较少特征的情况下保证算法识别的准确率,基于该框架设计的降维路面识别模型在测试集上的测试结果表明,模型在4 种路面上的识别精确率和召回率普遍在96%以上,而冰雪路识别精确率和良好沥青路识别召回率分别为94.15%和93.45%,相对于高维路面识别模型的下降幅度不超过3.2%,表明降维的路面识别模型保留了原始特征中大部分的信息,证明了模型解释的有效性,同时证明算法具有较高的识别精度.

(3)路面识别模型测试结果是基于随机采样的离线测试样本进行的,虽然达到了较高的识别精度,但对于车辆主动控制而言,算法的实时运行中可能产生的识别结果跳变也会对车辆控制产生一些影响,因此未来的研究工作中应加强路面识别模型对于时序数据的处理,提高分类性能.