基于机器学习的间接式胎压监测算法研究

于 璐，唐 亮*，魏凌涛，刘子俊

（1.北京林业大学 工学院，北京100091，中国； 2.清华大学 车辆与运载学院，北京100084，中国）

据交通管理部门统计（2017 年），高速公路发生的交通事故中，42%意外交通事故和70%的重大交通事故均由爆胎造成。事故发生时，车速越快，死亡率越高，当车辆时速达140 km/h 时，死亡率接近100%。胎压监测系统（tire pressure monitoring system, TPMS）是一种实时监测轮胎压力在异常出现时进行报警的系统，其在预防爆胎事故中起着至关重要的作用。中国继美国、欧盟、韩国之后，于2020 年1 月1 号开始执行乘用车强制安装胎压监测系统的法规，对胎压监测系统的发展起到了推动性的作用。

目前轮胎压力监测系统主要分为2 类：直接式轮胎压力监测系统（direct TPMS, DTPMS）和间接式轮胎压力监测系统（indirect TPMS, ITPMS）。直接式轮胎压力监测系统虽然有较为准确的优点，但是因为需要额外安装压力传感器，使其成本较高。间接式轮胎压力监测系统不需要加装任何设备，通过汽车制动防抱死系统（anti-lock brake system, ABS）内的轮速传感器获得轮速信号，完成一系列算法即可实现轮胎压力的监测，因此得到了更为广泛的应用。

间接式胎压监测有2 种较为经典的方法: 半径法和频率法。半径法的原理一种为通过轮胎半径值[1]、轮胎相对半径[2]、有效滚动半径[3]、ABS 轮速传感器发出的脉冲数[4]等与胎压的关系实时监测轮胎压力的变化；另一种为通过估计单位里程当量齿数[5]、比较千米脉冲数以及轮速的累积值[6]直接估计轮胎压力的数值。频率法的研究过程相对固定，首先建立轮胎振动模型，其次消除轮速传感器误差，然后重构轮速信号以及进行Fourier 变换，最后估计共振频率并进行欠压判断。频率法研究的创新点主要在于用不同的方法解决以上问题。其中消除轮速传感器误差使用到了Kalman 滤波[7]和弹性反向传播 (back propagation, BP)神经网络[8]等方法；轮速信号的重构和共振频率的估计通常使用插值法和经典谱估计法[9]。

机器学习在目标识别、故障诊断以及寿命预测等方面有着较为广泛的应用[10]。Bayesian 估计是一种基于统计学理论的常见的机器学习方法，主要应用在数据挖掘、故障诊断以及疾病预测模型等方面。近年来，在汽车领域也开始了一些应用，比如：基于Bayesian估计的环境车辆感知[11]，采用的Bayesian 优化方法对轨迹跟踪模型预测控制器的参数进行了优化[12]，基于Bayesian 网络的列控车载设备故障诊断[13]等。除了Bayesian 估计之外，还有一些其他的机器学习方法也被广泛应用。深度卷积神经网络用于检测切割轮的缺陷[14]，深度置信网络（deep belief networks, DBN）、深度Boltzmann 机（deep Boltzmann machine, DBM）、卷积神经网络（convolutional neural networks, CNN）和循环神经网络（recurrent neural network, RNN）用于机器的寿命预测和健康检测[15]，模糊决策树算法对癌症数据进行分类[16]。

本文将机器学习应用于间接式胎压监测系统，提出了一种新的轮胎压力监测方法。首先建立轮胎刚性环模型，在理论上证明了轮胎压力的变化会引起共振频率的偏移；然后对轮速信号进行预处理，使用最小二乘法（recursive least square, RLS）消除轮速传感器误差[17]，利用插值法重采样将轮速信号均匀化，利用Fourier 变换将时域轮速信号转化成频率域，并提取时域及频率域轮速信号的特征；最后进行轮胎压力状态估计，利用决策树剔除有问题的轮速信号，通过Bayesian 分类器估计轮胎压力状态。

1 轮胎振动模型的建立

参考文献[18]将轮胎模型简化为如图1 所示的四自由度弹簧阻尼系统，其中x和z分别表示水平和垂向位移，φ表示周向旋转角度，cx、cφ、ct和cs分别表示水平、周向、胎面和悬架阻尼。这些参数将用于轮胎振动模型仿真，具体定义及数值如表1 所示。

图1 轮胎振动模型

表1 轮胎振动模型仿真参数

车轮由轮辋和胎体2 个部分组成，假设轮胎的轮辋是刚体，形状不会因载荷产生变化，假设胎体是柔性的，在与路面接触的过程中产生形变。对轮辋和胎体进行动力学分析。

轮辋平移：

轮辋旋转：

带束环平移：

带束环旋转：

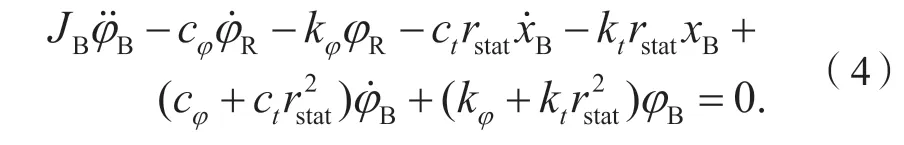
其中：xR和xB分别表示轮辋和带束环的位移，φR和φB分别表示轮辋和带束环的旋转角度。

选择X= [xRφRxBφB]T为状态空间矩阵，故可以将式（1）—（4）改写成状态空间函数，如式（5）所示。

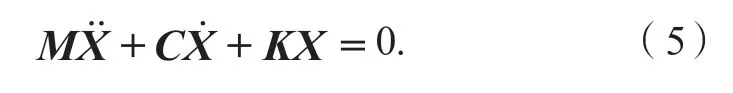
M和K分别为质量和刚度矩阵，如式 （6）、 （7）所示。

则固有频率fegi为：

将表1 参数代入到式中，计算得到刚性环轮胎模型的共振频率（f）为39.22、73.87、110.33、125.03 Hz。轮胎压力下降时轮胎刚度会减小，这里假设由于胎压的降低刚度减小5%，此时的共振频率分别为38.23、72、107.54、121.86 Hz。因此，轮胎压力的改变会导致其共振频率产生偏移，利用共振频率能够有效监测轮胎压力的变化。

图2所示是理想状态下轮速信号的幅频特性曲线，其中40 Hz 左右的共振峰由于欠压左移了约2.5 Hz，而15 Hz 左右的共振峰并没有因为欠压发生偏移，因此本文将利用40 Hz 左右的共振峰作为欠压判断的依据之一。

图2 理想状态下轮速信号的幅频特性曲线

2 轮速信号的预处理

基于机器学习的间接式胎压监测系统框架（如图3 所示），该方法包括轮速信号预处理和轮胎压力状态估计2 个部分。在轮速信号的预处理部分中，通过最小二乘法(RLS)估计轮速传感器误差，计算准确轮速，通过插值法重构轮速信号使其均匀化，将时域的轮速信号通过Fourier 变换转换到频率域，在时域和频率域上进行轮速信号特征的提取。在轮胎压力状态估计部分中，通过决策树剔除有问题的轮速信号，然后利用Bayesian 分类器判断轮胎压力状态。

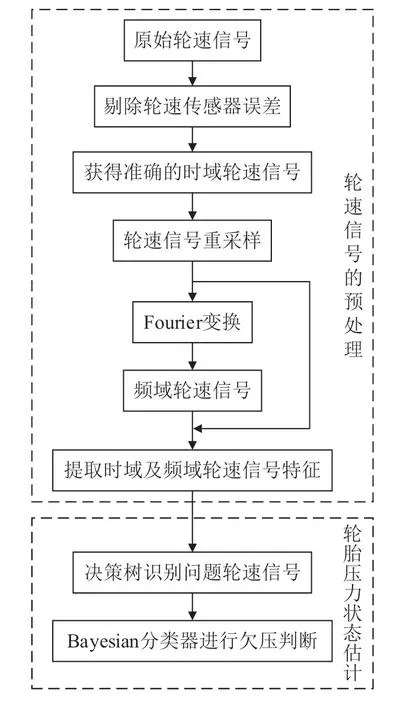
图3 基于机器学习的间接式胎压监测系统框架

显然，在实现胎压监测的过程中，轮速信号贯穿始终，所以准确地获取轮速信号尤为重要。轮速传感器由于其制造工艺和磨损的原因，使得传感器齿圈两齿之间的实际角度和理论角度存在偏差。为了减小因角度误差产生的影响，本文将利用RLS 法消除轮速传感器误差。

试验车驱动形式为前驱，试验过程中分别以30～70 km/h 的速度在平坦和颠簸路面上行驶，通过制动防抱死系统（ABS）分别采集左前轮正常胎压和欠压时的轮速信号。正常胎压为车型制造商推荐压力0.25 MPa，另根据乘用车轮胎气压监测系统的性能要求和试验方法（GB 26149-2017）将欠压时的压力设置为推荐胎压的75%，即0.19 MPa。

2.1 最小二乘法(RLS)消除轮速传感器误差

图4为处理时域轮速信号示意图，假设轮速传感器齿圈有Nt个齿，传感器总共采集到了齿圈旋转k圈的轮速信号。假设Δti(k)为轮速传感器齿圈旋转第k圈经过第i个齿的时间间隔，θi(k)为该齿的真实弧度，此时的旋转角速度如式(9)所示。图5 为轮速传感器误差示意图，理论上各齿应均匀分布于齿圈之上，相邻两齿弧度θ0可由式（10）计算得到。但由于制造误差让相邻两齿的弧度存在一个Δθi(k)的偏差，此时相邻两齿的真实弧度为θi(k)可由式（11）计算得到。

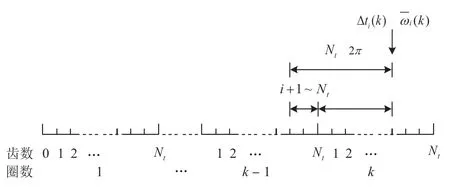
图4 时域轮速信号示意图

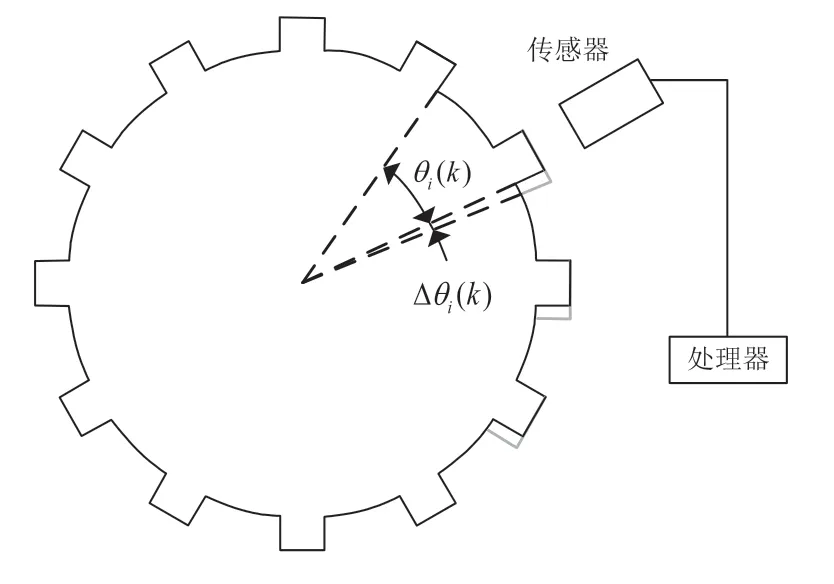
图5 轮速传感器误差示意图

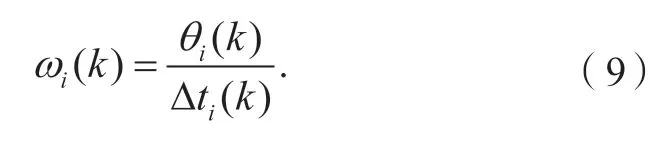
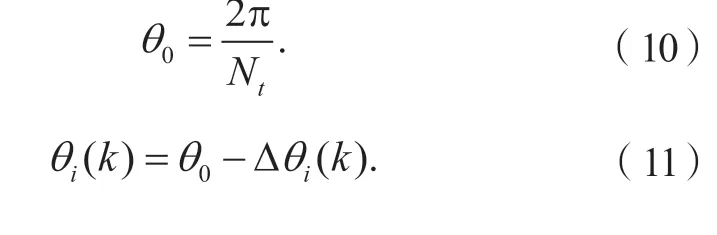
如图4 所示，第i个齿从第k-1 圈扫过传感器到第k圈再次扫过传感器正好旋转360°，经过Nt个齿。将齿圈第i个齿从k-1 圈转到第k圈的平均角速度近似为第i个齿在第k圈时的瞬时速度ωˉi(k)，如式（12）所示。此时，相邻两齿的真实弧度可通过式（13）计算得到。

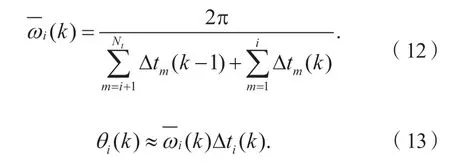
本文利用递归RLS 法消除制造误差，RLS 过程可以表示成算式（14）和式（15），其中分别是第i个齿在第k圈和第k-1 圈的误差估计值，p(k)是递归因子，为齿圈误差估计值与齿圈误差测量值之差。

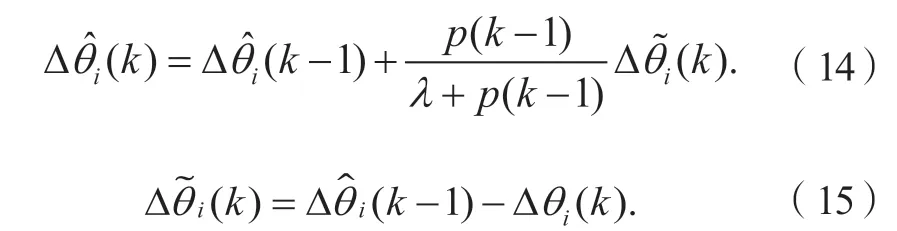
递归因子p(k)计算过程如式（16）所示，其中p(k)的初始值p(1) = 1，λ为遗忘因子且λ∈(0,1]。

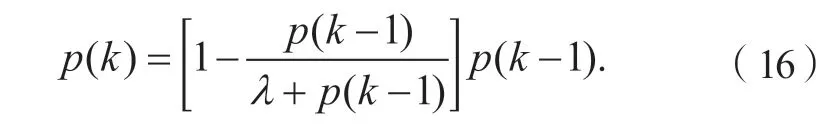
处理每组轮速信号的时候均进行一次误差的标定。标定原则为将每转一圈估算的齿的误差累加后取均值，如式（17）所示。

图6为轮速传感器误差估计的结果。图6a 为误差网格曲面图，x轴为齿数，y轴为轮速传感器齿圈旋转的圈数，z轴每圈齿轮误差估计结果。图6b 是图6a 的递归结果，即齿圈误差估计的最终结果。

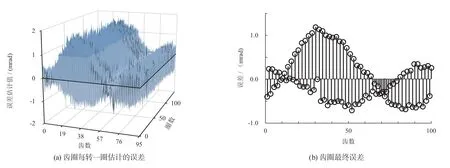
图6 轮速传感器齿圈误差估计结果

计算出轮速传感器制造误差之后，可以通过式（18）得到消除误差后的精确旋转速度，其中Δθi为最终的制造误差。由于轮速信号是通过轮速传感器上升沿激励得到的，所以此时的轮速信号在时域上是不均匀的，需要通过线性插值法将其重采样，获得时域上分布均匀的轮速信号。根据Nyquist 定理，采样频率超过目标频率[0,100] Hz 最高频率的2 倍即可，这里为了重采样之后轮速信号尽量不失真，选择了2 000 Hz 的采样频率。

由于后续需要在时域和频率轮速信号上分别进行特征的提取，所以时域的轮速信号需要进行Fourier 变换，而离散Fourier 变换对数据长度是有要求的，将轮速信号按7.5 s 的长度截断，既保证了进行Fourier 变换结果不失真又在现有数据基础分得尽可能多的组。

2.2 提取时域、频域轮速信号特征

利用机器学习实现间接式胎压监测需要对轮速信号进行特征提取。本文将提取23 个特征，包括2 个时域轮速信号特征、12 个原始频域轮速信号特征和9个平滑频域轮速信号特征。其中时域轮速信号 （如图7所示）已经得到，频域轮速信号（如图8 所示）需要将时域轮速信号进行高通滤波、Fourier 变换以及平滑处理后得到。

如图7 所示是4 种典型的时域轮速信号，包括正常轮速信号和分别存在速度过低、抖动过大和周期性噪声的问题轮速信号。

图8是4 种典型轮速信号的频谱图。图7a 为正常的时域轮速信号，均值为51 km/h，在0.5 km/h波动范围；图8a 为正常轮速信号的频谱图，可以看出3 个分别在15、42、58 Hz 附近的共振峰，这3 个共振峰正是在第1 部分提到的刚性环轮胎模型的共振峰。图7b 是一种典型的不适合做间接式胎压监测的轮速信号，其轮速过低且每隔一定时间发生一次突变；图8b 为图7b 的频谱图，频域轮速信号在40 Hz 左右没有波峰，所以不适合用于间接式胎压监测。图7c 为抖动过大的轮速信号，波动幅度接近0.8 km/h，这部分轮速信号是由于车辆行驶于颠簸路面上所造成的；图8c 的峰值在3 个特征频率附近没有图8a 明显，因此这类轮速信号也不适合用于间接式胎压监测。图7d 的轮速信号在红框处出现明显的周期性噪声，这部分噪声是由于没有完全剔除轮速传感器误差所造成的；图8d 在40 Hz 左右没有共振峰，故这种轮速信号不适合用于间接式胎压监测。综上所述，不适合进行间接式胎压监测的轮速信号包括速度太低的轮速信号、抖动过大的轮速信号和存在周期噪声的轮速信号。

从图7 和图8 可以看出，正常轮速信号和问题轮速信号可以通过时域轮速信号波动的大小和频域轮速信号的形状区分出来。由于共振峰值与轮胎压力相关，所以可以通过提取时域轮速信号的波动以及频域轮速信号的形状特征来进行轮胎压力的识别。本文提取了时域及频域轮速信号的23 个特征，包括时域轮速信号均值u和轮速波动的均方根ΔvRMS，原始频域轮速信号的前6 个共振峰的共振频率fR和峰值振幅AR，平滑频域轮速信号前3 个共振峰的共振频率fS、峰值AS和峰宽δfSw。

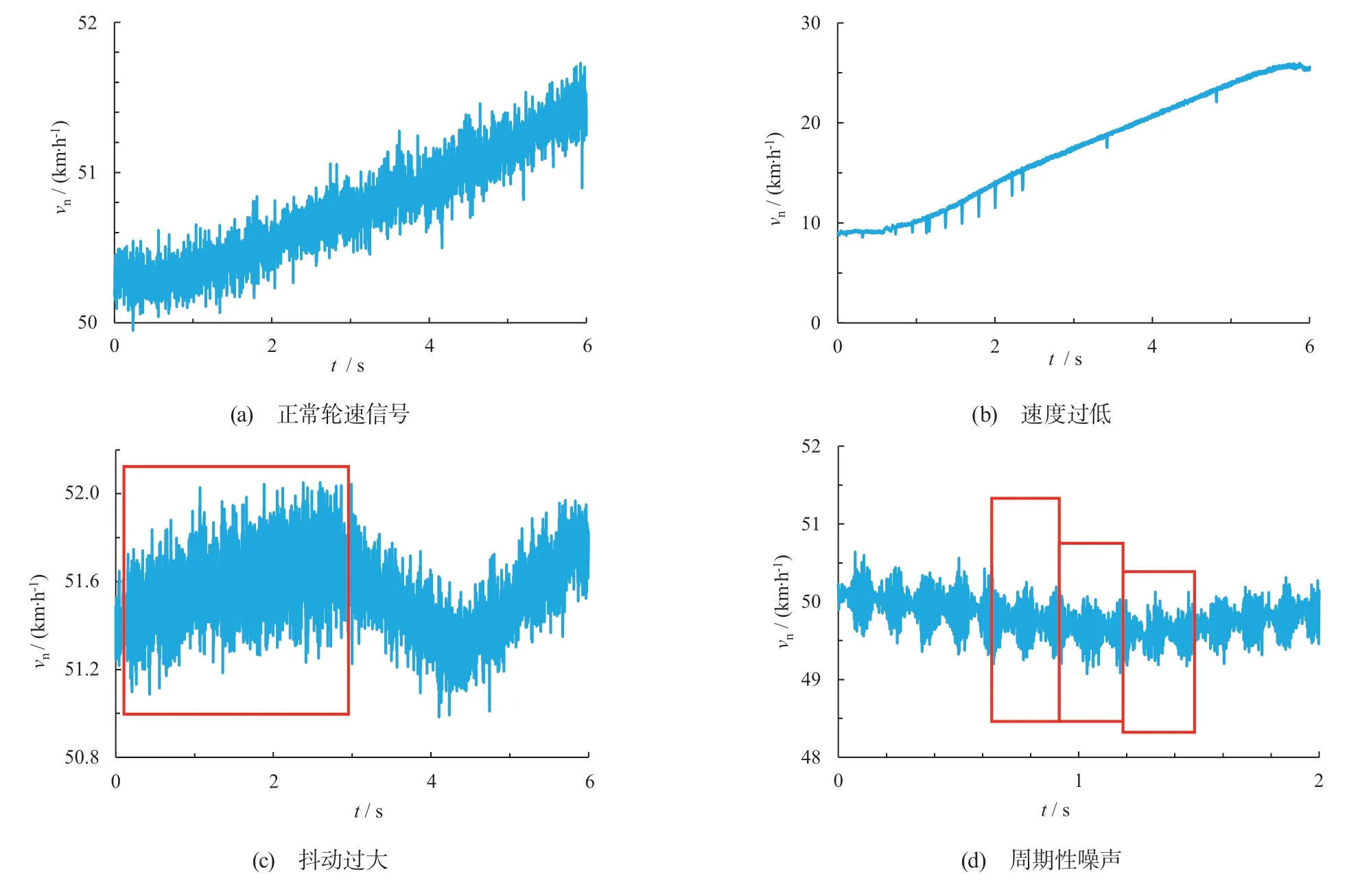
图7 典型时域轮速信号

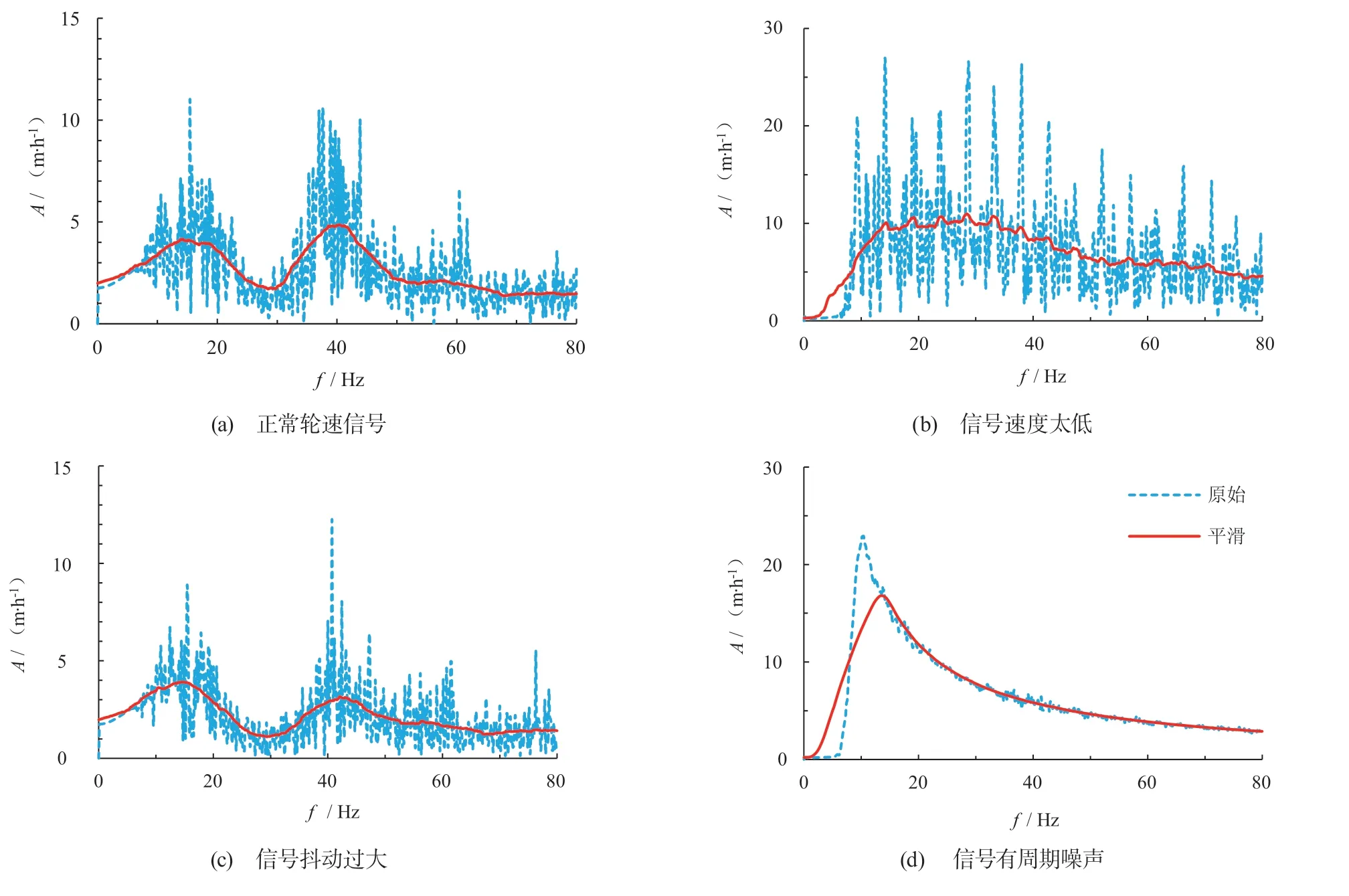
图8 典型时域轮速信号的频谱图

图9 为轮胎压力正常和欠压25%的轮速信号的原始频谱图，提取前6 个共振峰fR和AR作为该频谱图的特征，其中共振峰值是6 个间隔大于15 Hz 的共振频率所对应的振幅。以图9 正常胎压的前3 个共振峰为例，振幅分别为AR(1)= 16.2 m/h、AR(2)= 17.0 m/h、AR(3)= 8.5 m/h，共振频率分别为fR(1) = 14 Hz、fR(2) =38.43 Hz、fR(3) = 78.57 Hz。

图9 原始频域轮速信号

图10为图9 平滑后的频域轮速信号，取前3 个共振峰的共振频率fS、峰值AS和峰宽δfSw作为该频谱图的特征。

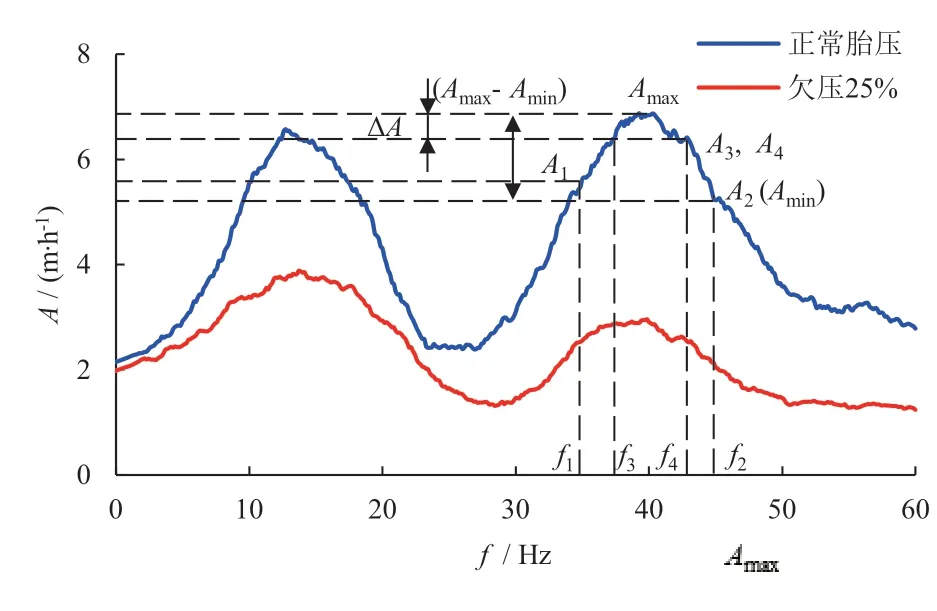
图10 平滑频域轮速信号

以40 Hz 左右的共振峰为例，假设[f1,f2]是一个包含期望频率40 Hz 的区间，Amin和Amax是期望区间内共振峰峰值的最小值和最大值，ΔA和共振频率fS如式（19）和式（20）所示，共振峰值AS为区间[f1,f2]内的最大振幅Amax，峰宽δfSw如式（21）所示。如果在区间[f1,f2]内没有找到期望的共振频率，那么此时的fS、AS以及δfSw均为0。为了对应轮胎振动模型的3 个固有频率，需要分别在[10, 20] Hz、[35, 45] Hz、[75,90] Hz 区间内提取共振峰的共振频率fS、峰值AS和峰宽δfSw。

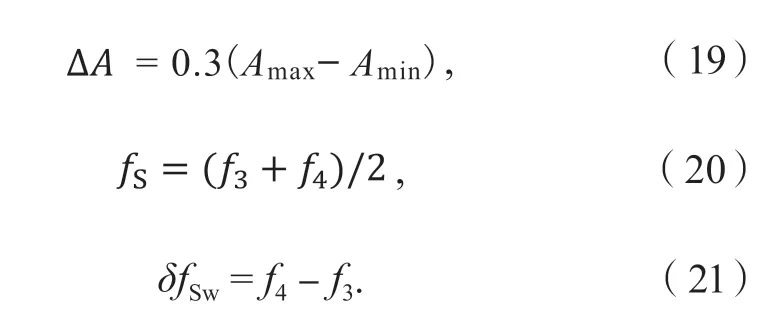
3 轮胎压力状态估计

本文对已获得的3 000 组数据分别进行时域和频域特征提取，并训练出一个可以将所有数据分为适合进行胎压监测的正常轮速信号和不适合进行胎压监测的问题轮速信号的决策树。正常轮速信号包括正常胎压采集的轮速信号和欠压25%采集的轮速信号。利用正常轮速信号训练Bayesian 分类器进而识别压力状态。

3.1 决策树剔除问题轮速信号

决策树具有预测速度快以及易于理解的优点。本文利用决策树将轮速信号分为2 类：其一是正常轮速信号，其二是不适合用于间接式胎压监测的问题轮速信号，其中问题轮速信号为第2 节提到的轮速过低、抖动过大和存在周期性噪声时采集的轮速信号。

在MATLAB Classification Learner 工具箱中，用3 000 个样本训练一个最大分裂数为15 的决策树，将这些样本分为5 组进行交叉验证，训练结果的准确率为98.9%。利用提取的时域及频域轮速信号特征训练的决策树示意图如图11 所示，其中圆圈表示正常轮速信号，三角表示问题轮速信号。

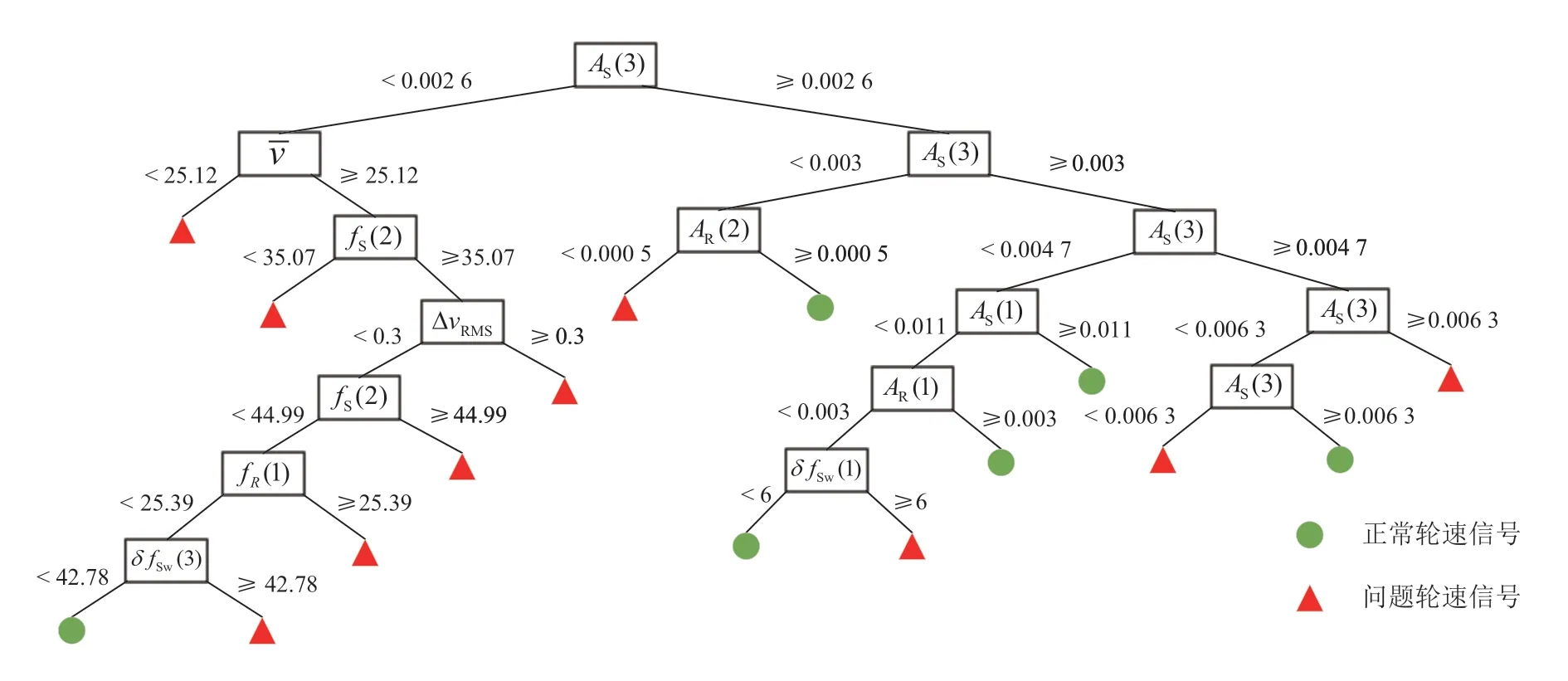
图11 决策树训练结果

根据决策树训练结果可以看出：区分正常轮速信号和问题轮速信号的主要依据为：

1） 原始频域轮速信号和平滑后的频域轮速信号的共振频率和峰值在一定的范围内，且形状接近正常胎压时的理想频域曲线；

2） 时域轮速信号不应该太小；

3） 时域轮速信号波动的均方根不应该太大。

车辆在行驶过程中，转弯、急加减速和行驶于颠簸路面时采集的轮速信号可能出现“问题轮速信号”的情况，但实际行驶过程中不会长时间处于这类工况，所以在实车应用过程中，选择在采集到这部分轮速信号的时关闭间接式胎压监测系统，防止误报。

3.2 Bayesian 分类器进行轮胎压力状态估计

由于采集的轮速信号对应的压力状态已知并且只分为正常胎压和欠压25% 这2 种，符合进行Bayesian 估计的先决条件，故本文决定采用此方法进行轮胎压力的识别。

首先，利用最大似然估计方法估计先验概率，假设样本总数为N，样本类型为Y，样本有Ck= (k= 1,2)，则不同压力状态的先验概率P为：

然后，建立最小误差率Bayesian 分类器。

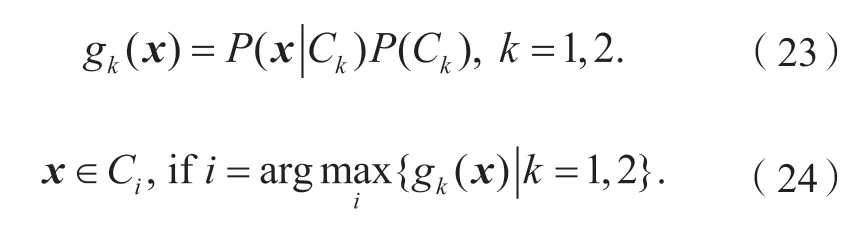
若样本x为d维向量，第k类样本的均值为mk，协方差为Sk，则其服从多元Gaussian 分布的条件概率密度为：

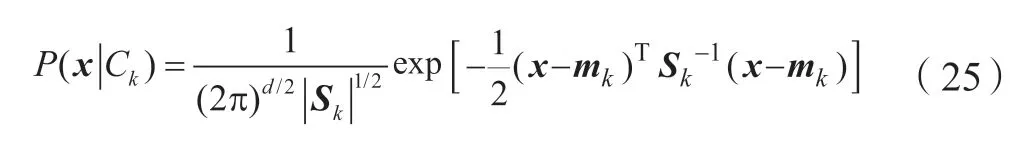
上式中|Sk|是Sk的行列式函数，T 是转置符号，Sk-1是Sk的逆矩阵。

如图12 所示为Bayesian 分类器算法流程图，利用最大似然估计方法估计先验概率，选正常轮速信号中的50%作为训练集剩余50%为测试集，依照压力状态将测试集中的特征分为正常胎压的特征和欠压25%的特征，利用Gaussian 分布计算条件概率密度，建立最小误差Bayesian 分类器，将测试集特征输入Bayesian 分类器，输出为此特征对应的压力状态：正常胎压或者欠压25%，根据预测结果计算Bayesian 分类器预测的准确度，预测准确度=预测正确的数量/总数量。

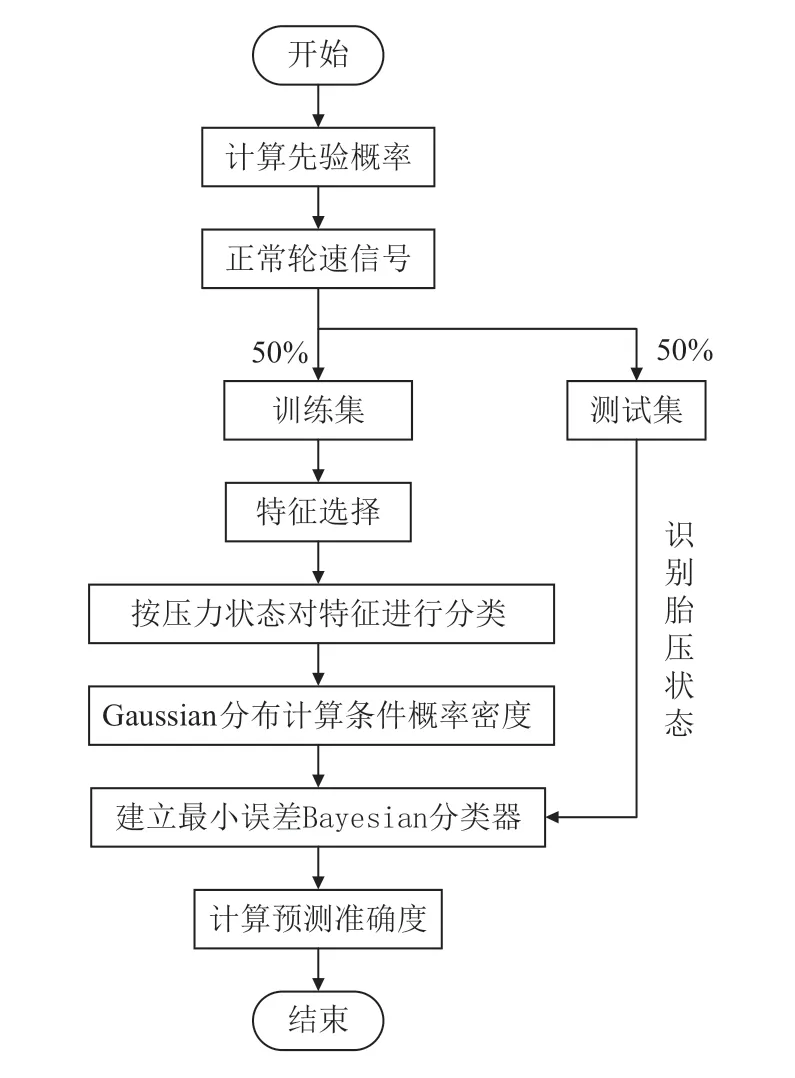
图12 Bayesian 分类器算法流程图

3.3 轮胎压力状态识别准确率

如图13 所示，通过2 个混淆矩阵对比2 种基于机器学习的间接式胎压监测方法的识别准确率，其中1 代表轮胎压力正常，2 代表轮胎欠压25%，3 代表问题轮速信号。一种方法是直接使用Bayesian 分类器识别轮胎压力状态，如图13a 所示混淆矩阵输出2 种压力状态，正常胎压和欠压25%，此时Bayesian 分类器识别准确率为60.8%，漏报比率为5.5%，误报比率为52.4%。另外一种方法是先利用决策树将轮速信号分为1 463 个正常轮速信号和1 537 个问题轮速信号，决策树的准确率为98.9%，然后依据正常轮速信号利用Bayesian 分类器识别轮胎压力状态，准确率为96.36%，与直接使用Bayesian 分类器相比，该方法的准确率更高。图13b 所示为当混淆矩阵输出正常胎压、欠压25%和问题轮速信号3 种类别时，识别准确率为91.6%，漏报比率为13.5%，误报比率为6.8%。

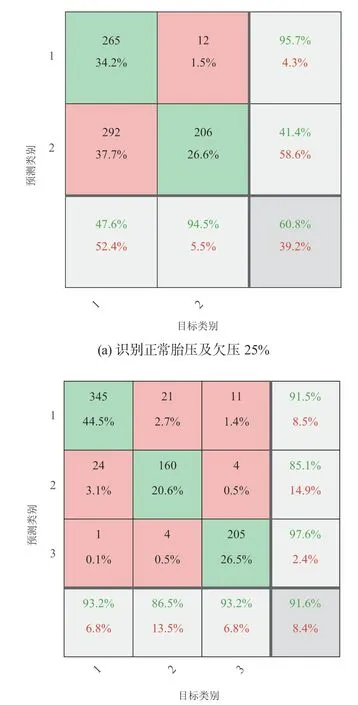
图13 利用Bayesian 分类器识别胎压力状态的结果

4 结 论

本文基于机器学习提出一种将决策树和Bayesian分类器结合在一起的间接式胎压监测方法，通过实车采集的轮速信号验证了算法的有效性。该方法与直接式胎压监测系统以及只使用Bayesian 分类器进行间接式胎压监测相比，成本较低且准确率更高，其准确率可达96.36%。