基于SSI-PSO 的汽车碰撞试验时序数据处理与分类方法

李 晗，刘 钊，朱 平

（1.上海交通大学 机械与动力工程学院，上海 200240，中国；2.上海交通大学 设计学院，上海 200240，中国）

假人响应曲线是汽车碰撞试验中从试验假人传感器采集得到的多组时序数据，是反映汽车安全性的重要数据。在进行汽车碰撞安全试验时，通常在每个试验假人上布置50～70 处传感器，以测量和记录碰撞发生时刻后300 ms 内各处的力、力矩、加速度、位移等信息，每组数据即具备时序、多变量、高维度等特性。基于安全法规和标准，汽车安全性评价和乘员损伤指标即通过假人响应曲线的峰值、累计值等信息计算。假人响应曲线中蕴含了大量信息，在工程开发过程中，同样会参考历史记录中相似的曲线波形，以评估当前乘员约束系统的设计状态、获取设计的参考信息。

然而，在面向工程应用开发的汽车碰撞安全数据统计和分析过程中发现，假人曲线数据存在一定量的位置信息不一致（标注错误）、试验工况标注缺失（标注缺失）等数据质量问题。这些问题在单次的工程开发过程中不会造成直接的影响；然而在基于数据挖掘的分析和应用过程中，则影响后续工程指标的提取和结论判定，亟需有效的数据治理方法。

在对汽车碰撞试验假人响应曲线进行数据挖掘与知识发现的过程中，特征的选择、参数的调整、模型的构造等问题可以转化为优化问题，数据模型的训练本身即为参数优化问题，因此优化算法是数据挖掘的重要的驱动工具[1-3]。启发式群智能类优化算法基于自组织的结构在优化过程中积累数据，并从数据中学习经验和知识以指导自身的优化搜索行为，是广义的机器学习方法[4]。智能优化算法在解决上述优化问题中取得了一定的效果，过早收敛而陷入局部最优解的问题仍阻碍着其进一步的应用[4-5]。

本文针对汽车碰撞安全试验假人曲线分类问题，基于社会蜘蛛粒子群优化算法，研究面向智能优化算法的优化问题转换和构造方法，提出优化驱动的碰撞试验多变量时序数据特征选择和分类方法，并利用汽车碰撞试验采集的曲线数据进行方法的测试和验证。

1 假人曲线数据分类问题描述

某公司通过汽车安全试验累积了大量假人响应数据，其中部分驾驶员假人头部、副驾驶侧假人头部的加速度响应曲线如图1 所示。其中：ax、ay、az为假人头部的3 向加速度。该数据集还包括：头、颈、胸、股骨、髌骨、胫骨等部位的位移、速度、加速度等信息，技术规范[6]规定的如何处理试验曲线并计算工程指标。

图1 汽车安全试验假人头部碰撞响应曲线数据（部分）

该公司的汽车安全试验假人碰撞响应曲线数据的部分统计信息如表1 所示。其中，曲线名称与曲线编号是各组曲线数据中均有标注的信息，记录来自试验过程的不同来源。曲线编号即根据曲线名称编译得到。

表1表明：实际数据集中存在着曲线编号与曲线名称不一致的情况，即存在同一个曲线名称对应多个曲线编号，或同一个曲线编号对应多个曲线名称。针对表1 所列举的统计信息，在曲线名称正确的前提下，根据曲线编号规则可以明确地指出在3 组曲线名称对应计数较少的曲线编号标注错误，其分别是由标注错位置、方向、位置导致的。而针对单一的曲线数据，则无法直接判断正确的标注应当遵从曲线名称或者曲线编号。

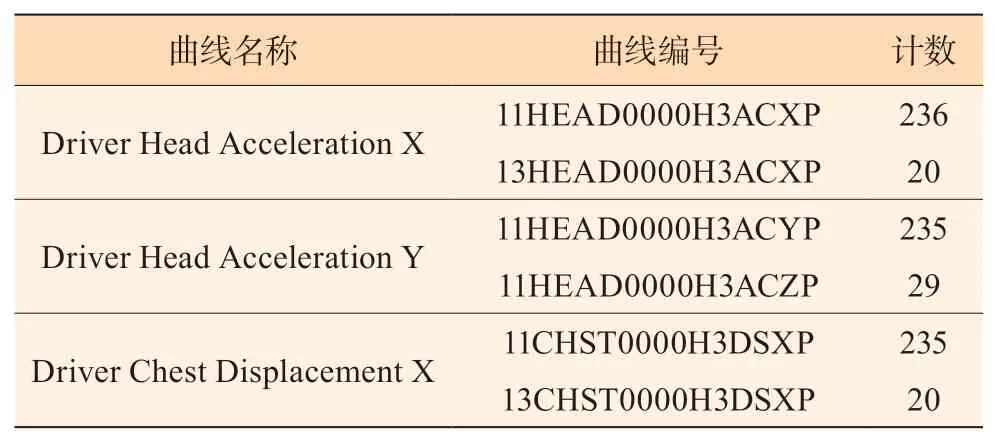
表1 汽车安全试验假人碰撞响应曲线数据统计信息（部分）

这些问题通常是由于试验人员操作不规范、失误、疏忽，数据遗漏等原因造成成套假人曲线的测量位置、工况缺失或标注错误等问题。例如在进行台架试验时，基于特定目的或仅需做单侧假人试验，而在进行传感器接入和配置时未全部设置正确。在这种情况下试验仍然是有效的，工程师亦能从试验结果中判断实际情况并获取有效信息；然而，在后续进行数据挖掘时，则需要发现并纠正此类数据标注问题，避免数据类别错误影响后续工程指标的提取和判断。

针对假人曲线数据存在的多种标注问题，需要建立有效的分类模型加以治理。由于假人曲线数据采集自多条通道，每条通道即包含3 000 个样本点，故属多变量高维时序数据，计算成本较高。一方面，基于技术规范对损伤指标进行提取，该种数据降维方法舍弃了大量的数据特征，数据差异较小，难以有效地建立区分数据采集位置、工况等信息的分类模型；另一方面，由于数据的强非线性和差异性，直接基于单一类别曲线亦难以建立精确的分类模型。

为实现对汽车碰撞安全试验假人曲线数据的缺失类别标注和错误标注检测、降低高维数据下的计算开销，需要研究有效的多变量时序数据特征处理和分类方法，利用多通道传感器采集的多变量时序数据构造特征处理问题和分类问题，并基于有效的优化算法进行求解。

2 社会蜘蛛粒子群优化算法

2.1 标准粒子群优化算法

根据启发式智能优化算法比喻（metaphor）来源的不同，可分为4 类：生物遗传类算法、物理法则类算法、群智能类算法、直接启发类算法（或称为人类活动启发的算法）。根据比喻义来源的分类法通常难以反映算法的机理，而根据算法核心迭代公式进行推导，可重新分为2 类：1) 直接搜索类算法，这类算法通常含有速度的概念，如中心力优化算法[7]、引力搜索算法[8]、粒子群优化算法[9]、人工蜂群算法[10]、蜻蜓算法[11]等；2)迭代选择类算法，这类算法在每步迭代后会对新产生的种群进行比较和选择，如遗传算法[12]、差分进化算法[13]、和弦搜索算法等[14]。

粒子群优化算法（particle swarm optimization，PSO）因其相对的易用性和有效性，被视为代表性的群智能优化算法，其通过模仿鸟类的捕食行为设计的算法迭代格式。针对最小化问题，有：

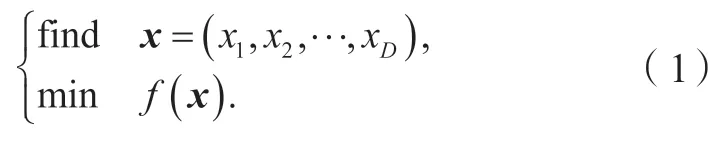
其中：x是D维设计变量，f(x)是优化目标函数。

粒子群优化算法构造了NP个粒子对公式(1)所示的D维问题进行迭代求解。以xi(t)和vi(t)分别表示第i个粒子在第t迭代步的位置和速度。位置即当前粒子对应的候选解，速度是当前粒子下一步寻优的移动方向，两者均为D维向量。pi(t)第i个粒子截止到第t迭代步所搜索到的个体最优解，g(t)是全部NP个粒子截止到第t迭代步所搜索到的全局最优解。适应度是比较粒子优劣的标准，通常直接利用目标函数构造适应度。

对于t+1 时刻的第i个粒子，位置更新公式为：

其中：xd,i和vd,i分别为xi和vi的第d维分量；速度更新公式为：

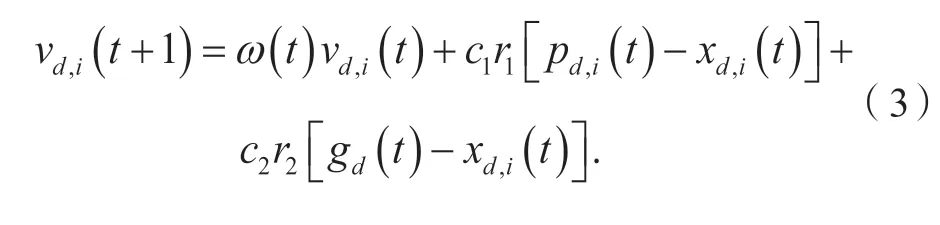
其中：pd,i和gd分别为pi和g的第d维分量；ω是惯性系数，通常随迭代过程由0.9 线性递减至0.1；c1和c2是两项对应的个体认知系数和社会认知系数，通常在[1,2]区间取值；r1和r2是[0, 1]区间均匀分布的随机数。

2.2 基于动态子种群的优化性能改进

粒子群优化算法的优化能力主要受限于其过早收敛现象。面向工程优化问题的特殊性，本研究基于一种改进的粒子群算法——社会蜘蛛粒子群算法（social spider inspired particle swarm optimization，SSI-PSO）[15]，通过设计新的种群结构和混合迭代策略增强算法的全局探索能力和局部搜索能力。基于标准粒子群算法框架，SSI-PSO 算法通过模仿社会蜘蛛（social spider）群落的个体间行为[16-17]，将全部粒子随机地划分为F 粒子（female particle）和M 粒子（male particle），各子种群策略具体如下。

2.2.1 F 粒子

F 粒子关注优化过程中的全局探索能力，由正F（positive female，PF）粒子和负F（negative female, NF）粒子组成。在每一轮迭代中，F 粒子随机地划分为PF粒子和NF 粒子，这2 类粒子适应度的优劣亦是随机的。

PF 粒子采用标准的速度更新公式，如式(4)所示。因为PF 粒子是从种群中随机选取的，所以避免了全部粒子均为高适应度或者低适应度等弱化多样性的情形。因此，PF 粒子是充分利用标准粒子群算法优势的基础。

其中：变量定义与式(3)相同。

NF 粒子的速度更新公式如式(5)所示。NF 粒子与PF 粒子处于相同状态时，倾向于向相反方向移动。考虑到实际优化问题通常是复杂且多峰的，NF 粒子的策略也有利于增加种群的多样性。同时，因为NF 粒子不再被个体最优解和全局最优解所吸引，过早收敛于局部最优解的问题亦可以在一定程度上缓解，进而更可能发现潜在的更优解。

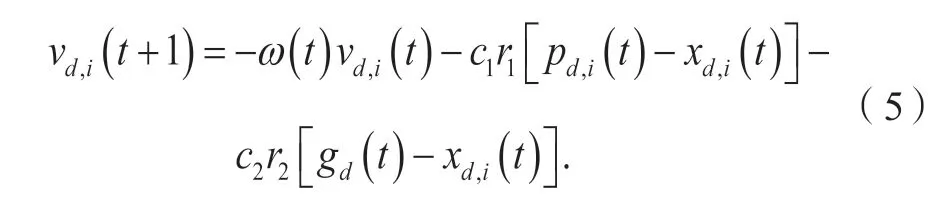
其中：变量定义与式(3)相同。

2.2.2 M 粒子

M 粒子关注优化过程中的局部搜索能力，由支配性M（dominant male, DM）粒子和非支配性M（nondominant male, NM）粒子组成。与F粒子随机划分不同，在每一轮迭代中先对M 粒子进行适应度排序，适应度高的为DM 粒子，适应度低的为NM 粒子。

尽管在算法设计过程中不希望过早地收敛于局部最优解，但一般认为最终的全局最优解可能在局部最优解附近。因此，具有较高适应度的DM 粒子采用局部搜索策略，其修改后的速度更新公式为

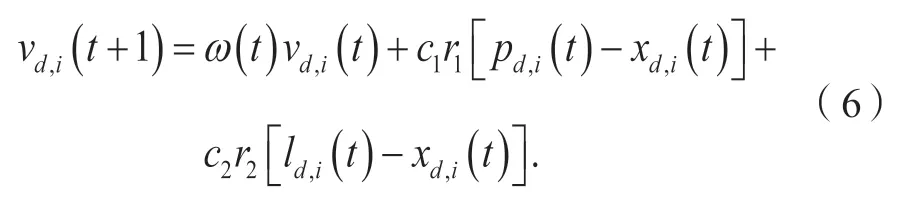
其中：变量定义与公式(3)相同。此外，利用第i个粒子当前的局部最优解li(t)替代了全局最优解g(t)。局部最优解是从距离当前粒子最近的LR×NP个个体最优解确定的。LR是预设的局部搜索范围，在确定局部的搜索范围后，距离为确定候选个体最优解后，从中选择适应度最好的候选个体最优解作为当前粒子的局部最优解。局部最优解的更新公式为

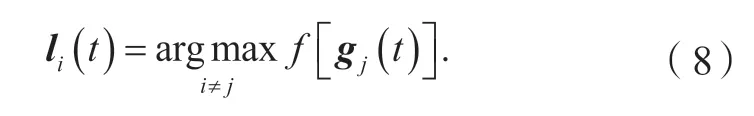
NM 粒子即适应度较低的M 粒子，其在迭代过程中向着当前最优解移动，以期潜在的提升和发现。其速度更新公式为

其中：变量定义与式(3)相同。

本研究所基于的SSI-PSO 算法流程如图2 所示。

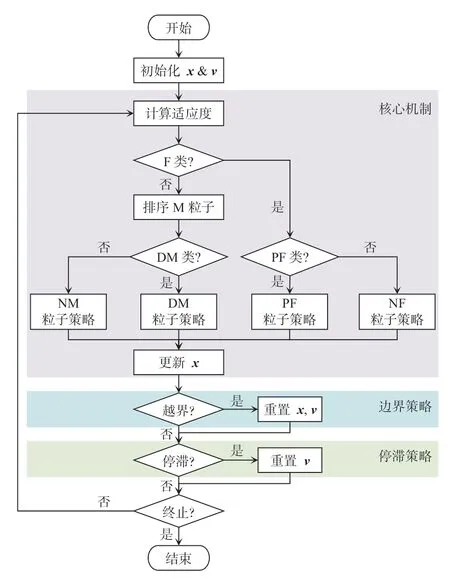
图2 SSI-PSO 算法流程

2.3 优化算法性能验证

为验证SSI-PSO 算法的有效性，选取9 个广泛使用的启发式优化算法作为对比，包括：人工蜂群算法（ABC）、蜻蜓算法（DA）、差分进化算法（DE）、遗传算法（GA）、引力搜索算法（GSA）、和旋搜索算法（HS）、标准粒子群算法（PSO）、蜘蛛搜索算法（SSO）[18]。测试函数是2017 年进化计算大会（2017 Congress on Evolutionary Computation, CEC 2017）提出的无约束函数，测试函数的维度D分别设置为30、50 和100，变量取值限制在[-100, 100]区间。SSI-PSO 算法所使用的粒子数量NP为40，速度更新公式的c1和c2分别设置为1.25 和1.75，惯性系数ω随迭代过程从0.9 线性下降到0.1。对比算法的粒子数同样设置为40，其他参数设置采用其文献推荐的默认值[8-14,18]。每轮测试中，限制目标函数评估次数为问题维度D的10 000 倍。以保证结果的可比性，每组测试重复50 次以获取稳定的结果度量和统计信息。

测试结束后，依次对每个问题下各个算法50 次求解的最小目标值的均值和标准差进行递减排序，将排序序号作为对应方法的得分，即排名越靠后、数值越小、结果越好。为更加直观地展示算法的性能差异，将同一项目中各函数下的分数相加，绘制于得分图上。得分即优化算法寻优结果的绝对好坏。

图3为在CEC 2017 测试函数上，SSI-PSO 算法与其他9 种优化算法的性能表现的对比。显然SSI-PSO算法（图3 中标记为SSI）在各个维度上均取得了最高总分，其寻优能力满足下一步的数据处理问题的应用。

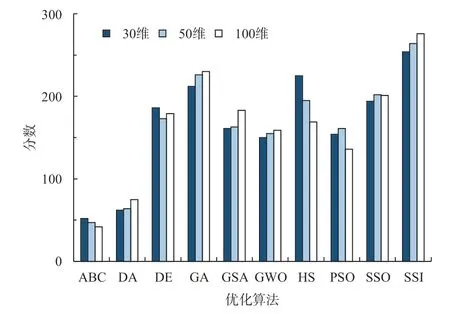
图3 SSI-PSO 算法与其他9 种优化算法对比

3 假人曲线数据处理方法

针对汽车碰撞安全试验假人曲线数据的分类问题，基于SSI-PSO 优化算法，本文提出一种优化驱动的曲线数据特征处理与分类模型构建方法。该方法包含2 个阶段：第1 阶段利用优化算法进行假人曲线数据的特征处理；第2 阶段利用优化算法进行浅层神经网络的曲线分类模型构造。

3.1 基于优化的碰撞曲线数据特征处理

不同于从单一设备长期采集且同一变量所有数据在时间上连续的信号类时序数据，汽车安全试验假人曲线仅在试验测量范围内（即碰撞发生时刻后的300 ms 内）是连续的，且大量采集的多通道数据是并列、独立且等长度的，即为高维、多变量问题。

3.1.1 选择设计变量

数据模型所耗费的计算资源通常与数据维度正相关，即高维数据耗费的计算资源相对较高。而由于假人响应数据时序采集的特性，可通过对每类曲线数据进行重采样而达到降维的目的，以提高计算效率[19-20]；同时，由于每类曲线以同等的信息密度记录了不同的工程信息，而这些信息在实际研发过程中被不同程度地参考，则可通过配置每类曲线的权重的方式强化反映关键信息的曲线在决策模型训练中的占比，进而提高模型精度。因此，本研究所提出方法将时序数据的重采样数量、多变量数据的各曲线权重构造为优化变量，通过对单次试验同一个假人采集得到的多个类别曲线进行不同密度的采样、加权和拼接，将多变量时序数据构造为一般的单变量结构化数据。

对于曲线数据集C中的样本为

其中：函数stack(·)表示通过顺序拼接操作扩充一维向量。给定向量M= {m1,m2, … ,mp}和N= {n1,n2,… ,nq}，若

则

其中：c'和xw分别表示一条重采样后的曲线数据和其对应的合并权重。曲线c'依据设计变量xs对原始曲线c重采样得

其中：函数resample(·)表示重采样过程。

3.1.2 定义优化目标

本方法中优化的目的是确定最佳的曲线数据预处理方法，具体到优化算法定义中，优化目标为多个基础分类器的混合折交叉验证分类精度，其构造方式如图4 所示。其中：基础分类器选择决策树（decision tree，DT）、K 近邻分类器（K-nearest neighbor，KNN）和支持向量机分类器（support vector classifier，SVC）等3类监督学习方法[21-22]。

图4 基于混合交叉验证分类精度构造目标函数

该优化目标的定义使得进行曲线特征处理的同时进行模型构建，可以归类为广义的包裹式特征选择过程。分类性能的度量指标为预测精度：

其中：ŷi是第i个样本对应的预测标签；yi是第i个样本的真实标签；nsam是样本数量；I(x)是指标函数：

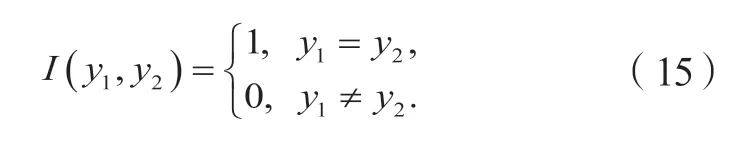
3.1.3 构造优化问题

所提出方法不需要构造特殊的约束函数，而是直接约束优化变量中对应曲线采样点数量的部分为整数，同时约束采样点数量和权重的上下限。最终，构造优化问题如下：

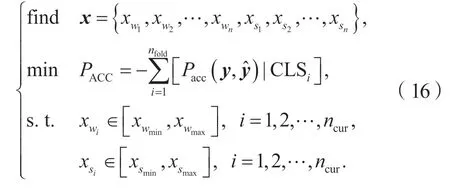
其中：nfold是交叉验证次数；ncur是曲线的类别数； CLS为基于混合交叉验证训练分类器：

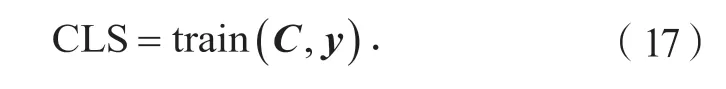
其中：函数train(·)表示模型训练过程；C是曲线数据；y是曲线数据对应的类别标注。

3.2 基于浅层神经网络的曲线分类模型构造

神经网络（neural networks，NN）模型由一系列的非线性数学模型组成，适用于多种响应预测和分类任务，其高度灵活的理论性质使之成为通用近似器[23-24]。在神经网络模型的各感知层中，首层（第0 层）被定义为输入层，末层被定义为输出层，其他层为隐藏层。每个感知层由神经元组成，各个神经元接收前一层输入的信息，并向后一层传送信号，即净激活值（输出）。第l层的净激活值zl为：

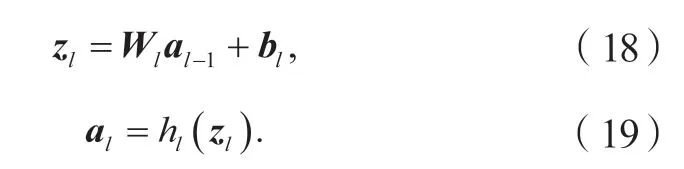
其中：al为第l层的激活值；a0即输入数据x；bl为自l–1 层到l层的偏置；Wl为自l–1 层到l层的权值矩阵；hl(·)为l层的激活函数。

随着神经网络模型训练方法的发展，具有少量隐藏层的浅层神经网络（shallow neural network，SNN）即能取得较好的拟合效果，并更为适合处理较小规模数据的问题。因此，本研究利用浅层神经网络构建分类器。尽管浅层神经网络模型的参数相较于深度神经网络模型大大减少，但仍需要对模型结构进行设计，以避免不合适的神经网络结构制约其分类性能。

3.2.1 选择设计变量

输入数据和输出数据的结构确定后，神经网络的结构由隐藏层的层数和每层的神经元数量决定，因此将隐藏层层数和神经元个数作为设计对象。由于优化算法需要在固定的变量空间内搜索，为方便计算，以nl维向量xn表示设计变量。其中nl为隐藏层层数的上限，xn在每个维度上的分量即为对应隐藏层上神经元的个数。在迭代过程中，若某个维度的分量小于设定阈值后，则在构建神经网络模型过程中删除该层，即实现了隐藏层层数的设计。

3.2.2 定义优化目标函数

基于设计变量的信息构建神经网络模型，以所构建的神经网络模型对测试样本的交叉验证精度为优化目标。选择S 形函数（或称sigmoid 函数）作为隐藏层和输出层的激活函数，并将函数值域转换到[-1,1]，以便于模型训练：

在神经网络模型的训练过程中，选则交叉熵（cross entropy，CE）作为损失函数：

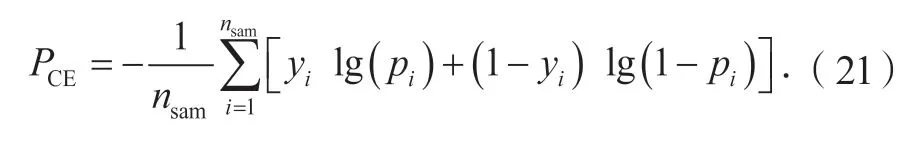
其中：yi是第i个样本的标签（正类为1，负类为0）；pi是对第i个样本预测为正类的概率；nsam是样本数量。

3.2.3 构造优化问题

所提出方法不需要构造特殊的约束函数，而是直接约束优化变量为整数，同时约束设计变量的上下限。最终，构造优化问题如下：

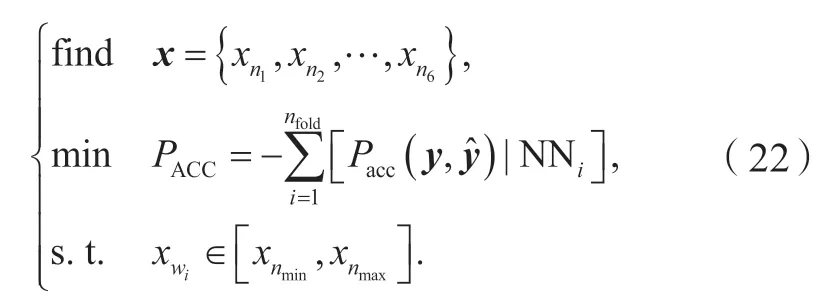
其中：nfold是交叉验证次数； NN 为神经网络模型。

3.3 本文方法流程及步骤

本文所提出的两阶段方法流程如图5 所示。

图5 本文方法流程图

步骤如下：

阶段1 将假人曲线数据各类别曲线的采样数量和曲线权重作为设计变量，最大化当前构造数据训练基础分类器分类混合交叉验证精度为优化目标，利用SSI-PSO 算法进行采样数量和曲线权重的寻优计算。

阶段2 获取最优化的采样数量和曲线权重，将多变量时序数据构造为降低维度的单变量时序数据，基于SSI-PSO 优化算法构造神经网络结构，进而训练浅层神经网络，以进一步提高模型精度。

4 碰撞试验假人响应曲线数据集应用

为充分阐释本文所提出两阶段方法的特性并验证其有效性，本节基于某公司整车碰撞试验数据进行对比分析。试验数据包括对整车碰撞试验中从第50 百分位假人采集得到的315 组试验数据，每组曲线包含23条响应曲线，即头部加速度ax、ay、az，颈部力Fx、Fz及力矩My，胸部变形Dches，左、右大腿压缩力Fz，左、右膝关节滑动位移Dknee，左、右小腿上、下胫骨力Fz及力矩Mx、My。每条曲线以0.1 ms 间隔采集自碰撞开始后的300 ms，即3 000 个数据点。每组数据的标注为其测量位置，即分类整组曲线采集自前排驾驶员侧假人或前排副驾驶员侧假人。

4.1 特征处理策略对比分析

4.1.1 采样范围对比分析

在优化过程中，适度缩减设计变量的可行域有利于提高优化算法的搜索效率；此外，在本方法中，曲线采样这一设计变量同时影响分类模型的规模，适度缩减设计域同样有利于降低分类模型的建模开销。为对比分析采样量的影响，从区间[3,3000]中离散地选取3、10、30、150、300、600、900、1 500、1 800、2 000、2 400、3 000 等12 个采样水平，即控制曲线的采样率在0.1%～100%范围内。随后，基于3.1.2 节所提出的混合交叉验证方法构造目标函数，选择决策树、支持向量机和k 近邻分类器作为基础分类器，并测试其分类精度。

训练数据集和测试数据集的样本划分为4:1，每组测试重复10 次以获取稳定的统计结果。为直观地展示不同采样点下所建立模型的预测精度Pacc及其波动情况，基于重复测试结果绘制统计图，如图6 所示。图6 中横坐标为不同的采样率Rsam，纵坐标为对应数据所建立的模型分类准确度和单次计算时间。

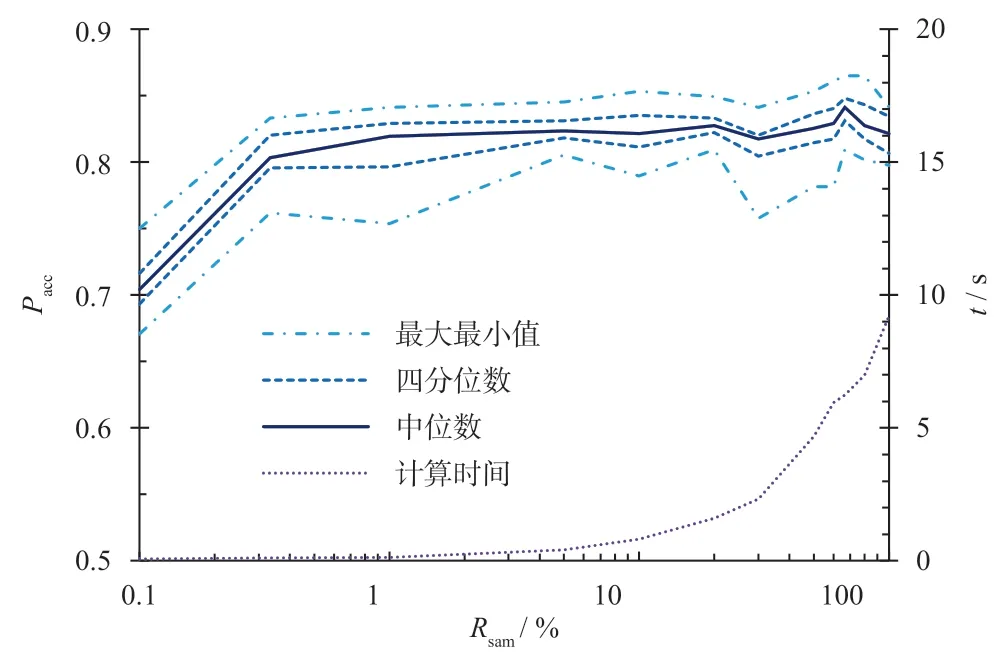
图6 不同采样点的基础分类器混合交叉验证精度

由计算结果分析可得，各组测试所得到的基础分类器混合交叉验证精度整体上与采样点的数量呈现正相关性，并具有一定的波动性。当采样点过少时 （如0.1%采样率），则无法训练得到有效的分类模型。此外，训练分类模型所花费的时间随采样点的增加而上升得更为明显；而模型的分类精度并未得到显著提升，因此优化调整曲线数据的样本点数量是可行的。

根据计算结果，30 至600 采样点的区间范围内即在显著降低计算时间的前提下维持一定的模型精度。由于未对数据特征做进一步处理，此时模型精度的绝对水平和波动情况均未达到应用要求，而在后续优化问题设置中，可将[30, 600]作为优化变量区间。

4.1.2 优化参数设置

利用SSI-PSO 算法进行优化设计，同时设置两组对照试验用以分析本文所提出方法的特性，各优化问题的粒子数和迭代次数均设置为100，即函数评估次数为104。为同时优化样本数据中23 条曲线的采样数量和合并权重，故优化问题的维度为46。此外，3 组测试的区别如下：

测试1 固定采样数量为300，在[-1, 1]范围内优化曲线权重；

测试2 固定曲线权重为1，在[10, 600]范围内优化采样数量；

测试3 按测试1、2 的范围同时优化曲线权重和采样数量。

4.1.3 优化结果与分析

各组试验重复测试10 次，并提取统计信息，其结果如表2 所示。

表2 特征优化问题的计算结果

由测试结果可得：在利用SSI-PSO 算法对样本曲线数据的采样数量和合并权重进行优化后，平均采样率接近，即均有效降低数据维度的同时可提高分类模型的混合交叉验证精度；单独优化采样数量或合并权重后的分类模型精度相近，而本研究所提出的同时优化策略进一步提高了模型分类精度。

4.2 分类模型建立对比分析

4.2.1 建模方法分析

本节首先对不同的神经网络结构进行测试，包括1至4 层不等的隐藏层数量，以及每层隐藏层中10 至40个不等的神经元数量。为直观地展示不同方法及不同神经网络模型结构所建立模型的精度Pacc及其波动情况，基于重复测试结果绘制箱线图，如图7 所示。

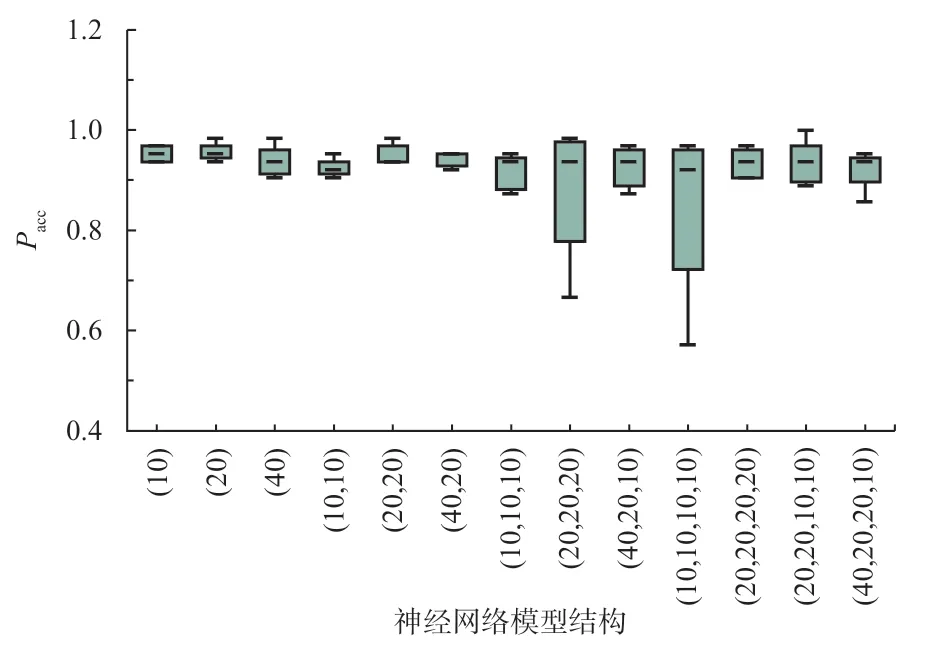
图7 不同分类器的分类精度

图7 中，以数组的形式表示不同的神经网络模型结构，括号内数组长度表示隐藏层数量，数值表示对应隐藏层神经元数量。由测试结果可得：小规模的浅层神经网络经过充分的训练过程即可得到较高精度；另一方面，由于训练样本相对于特征数量是有限的，引入过多的神经元后，同样不利于模型精度的提升。因此，两阶段分类模型中的浅层神经网络模型结构基于后续的优化策略确定，以减少经验设计的影响。

4.2.2 优化过程分析

利用SSI-PSO 算法进行优化设计，粒子数设置为40，迭代次数设置为100。此外，变量维度设置为6，即允许的最大隐藏层数量为6 层。计算优化目标时，所接受的最小神经元数量为10，即某维度变量小于10 时则删除该层；若全部维度小于10，则设定为单隐藏层10 个神经元。设计变量的采样范围为[–20, 80]，下界小于可接受最小神经元数量，通过此策略控制可行域趋向于较小规模的神经网络结构。

在迭代优化过程中，提取全局最优解在迭代路径上的关键点。因为全局最优解总是随迭代过程提升或持平的，因此将全局最优解对应的神经网络性能表现Pacc作为横坐标、将全局最优解对应的神经网络神经元总数Nneu作为纵坐标，并以不同符号区分全局最优解对应的神经网络隐藏层层数，绘制于图8。

图8 优化过程的历史全局最优解

在初始化阶段，由于粒子分布较为广泛、均匀，所对应的神经网络隐藏层数量亦多；随着迭代进程的继续，隐藏层层数和神经元个数均有所下降，这一趋势符合对浅层神经网络性能的预期。最终，优化过程收敛在单隐藏层26 个神经元的神经网络结构中。

4.2.3 结果对比

基于4.1 节针对曲线采样数量和合并权重的3 组测试的优化结果重新处理样本数据，进而训练包含26 个隐神经元的单隐藏层的浅层神经网络模型（OptNN）。此外，选择决策树分类器（DT）、K 近邻分类器（KNN）和支持向量机分类器（SVM）作为测试的对照组。为直观地展示基于不同测试优化结果所建立模型的精度及其波动情况，基于重复测试结果绘制箱线图，如图9所示。

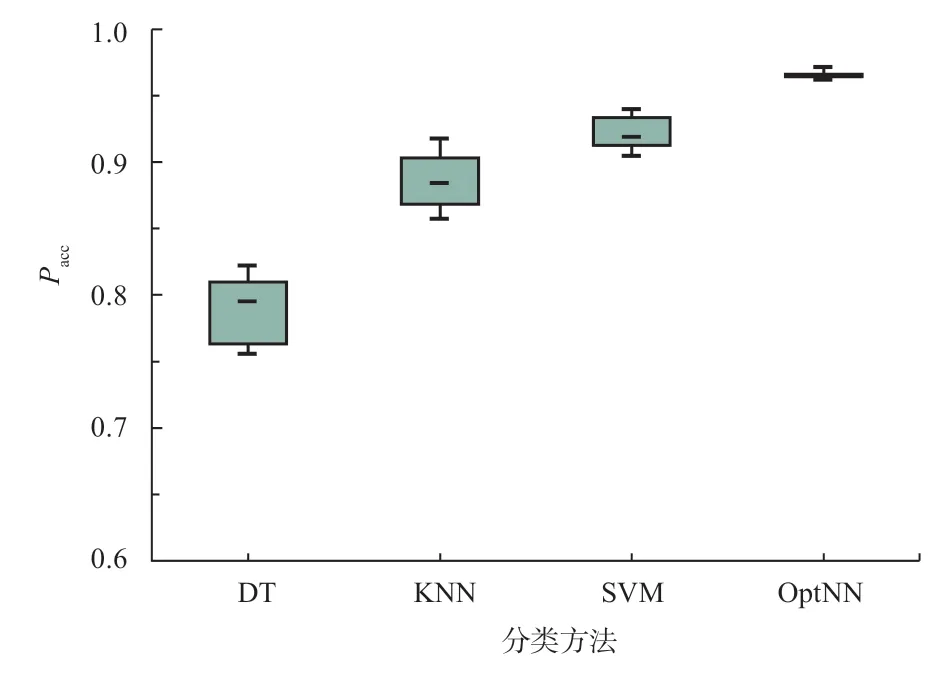
图9 基于最优采样和加权特征处理的模型分类精度

由测试结果可得：相对于决策树的 （0.790 ±0.022）、K 近邻分类器的（0.886 ± 0.019）和支持向量机的（0.922 ± 0.011），基于最优采样和加权特征处理建立的两阶段分类模型取得了最高的分类精度（0.965± 0.003）；同时，该结果的波动性较小，即保持了较高的稳定性。对比前序测试的结果，同时优化采样点和权重的策略优势延续到了第2 阶段模型构建中，使得分类精度得到了进一步的提升。对比未经特征处理和模型结构优化的分类模型精度，本研究所提出方法的分类精度从82.1%提升至96.5%，相对提升17.5%。

综上所述，本文所提出的两步式方法在碰撞试验假人多变量时序数据分类问题上是有效的。

5 结 论

本文针对汽车碰撞安全试验假人响应曲线数据存在的标注错误和缺失问题，提出优化驱动的两阶段碰撞试验多变量时序数据特征选择和分类方法，本文方法采用2 阶段策略：

在第1 阶段中，将采样密度和曲线权重作为设计变量，通过混合交叉验证精度构造目标函数，以优化的方式同时对曲线数据进行转换和特征选择（降维）；

在第2 阶段中，将用于构建分类模型的神经网络结构中的隐藏层数量和神经元个数作为设计变量，以优化的方式获取最佳结构设计。利用汽车碰撞试验数据进行测试和验证。

结果表明：本文方法可获得面向假人曲线数据分类的最佳特征组合方式与神经网络结构，其中假人响应曲线分类任务适合选用较小规模的浅层神经网络模型；基于本文方法，假人曲线分类模型性能提升17.5%、精度达到96.5%。从而，实现了对碰撞试验假人响应曲线标注信息的有效分类。