两级式半主动磁流变抗冲击座椅悬架系统设计与仿真

亓 昌，徐 博，余 洁，杨 姝，2，3*

（1.大连理工大学 汽车工程学院，大连 116024，中国；2.汽车安全与节能国家重点实验室(清华大学)，北京，100084，中国；3.大连理工大学宁波研究院，宁波，315016，中国）

地雷和简易爆炸装置(improvised explosive device,IED)产生的爆炸冲击载荷是军用车辆和特种车辆乘员安全的主要威胁。随着车辆底部防护结构性能的不断提升，车底爆炸导致的乘员致死率大幅下降；但与此同时，车底刚度的提高导致爆炸冲击载荷下地板加速度过大，容易造成乘员下肢损伤。这是目前车辆抗爆设计中亟待解决的难题[1]。

抗冲击座椅是降低车底爆炸载荷下乘员伤害的重要部件，其性能设计对于车辆抗地雷安全至为重要[2]。抗冲击座椅是乘员与车体之间的主要接触途径，也是爆炸冲击载荷传递路径中的重要环节。抗冲击座椅通常独立设计，通过溃缩装置衰减冲击能量，以减小传递到人体的载荷。研究表明，一个具有大工作行程和足够弹性的抗冲击座椅能减少冲击脉冲峰值60%以上[3]。在车底爆炸冲击下，乘员下肢是主要受伤部位之一；车体底板在爆炸载荷下的高速变形破损会导致乘员脚部和小腿的严重损伤。为此，将脚垫整合到座椅上，使乘员脚部尽量远离爆炸源是目前的主要设计思路。但另一方面，安装在座椅上的脚垫隔断了人体与车体底板间的接触，而由路面激励产生的车身振动，经过轮胎、悬架和座椅后传递给乘员，易引起人体垂向共振，影响乘坐舒适性[4-5]。因此，抗冲击座椅的设计需要兼顾车辆的防护性和平顺性，属于多学科设计问题。

目前，国内外针对车辆抗冲击座椅的研究主要集中在爆炸载荷下座椅悬架系统的防护性能设计，对座椅的平顺性研究较少[6]。CHENG Ming 等[7]研究表明，乘员盆骨加速度峰值直接受座椅悬架性能的影响，并提出使用座椅跌落试验平台替代爆炸试验对抗冲击座椅进行性能分析以降低难度。DONG Yanpeng 和LÜ Zhenhua[8]提出一种带有多级非线性悬架的抗冲击座椅，并研究了悬架刚度系数和阻尼系数对座椅抗冲击性能的影响。魏然等[9]研究了某防护型车辆受爆炸冲击时的乘员损伤，以乘员小腿、颈部力矩为目标函数，建立了车底结构及座椅系统设计的优化模型。

针对座椅悬架刚度和阻尼的设计能有效提升座椅的抗冲击性能，并在一定程度上改善其平顺性。然而，抗冲击座椅的平顺性和抗爆性对其悬架性能的要求并不相同，甚至相互冲突。平顺性要求低刚度和低阻尼特性的座椅悬架，以减小路面激励产生的车身振动；而抗爆性则要求高刚度和高阻尼特性的座椅悬架，以尽可能多地衰减冲击波传递至人体的能量，降低乘员的受伤风险。目前，被动式抗冲击座椅悬架的线性或弱非线性刚度和阻尼特性决定了其只能满足抗冲击座椅特定工况或单一目标性能，难以同时满足对抗爆性和平顺性的不同要求。

近年来，智能材料技术的发展催生了一种采用磁流变液的可控式减振器。因其具有响应快、动态范围大、可靠性高、能耗小、结构简单、适应性强[10]等优点，在车辆抗冲击座椅上应用潜力很大。CHOI Young-Tai和N. M. Wereley[11]针对抗冲击座椅悬架设计了半主动非线性最优控制算法，同时用于振动和冲击控制。BAI Xianxu 等[12]开发了磁流变半主动座椅悬架系统的混合控制器，并针对振动和冲击的不同目标设计了相应的控制策略。上述控制算法和策略均试图在同一缓冲装置上同时实现减振与缓冲，这对于装置本身的控制精度和响应速度要求很高，实现难度大。

本文提出一种面向军用车辆和特种车辆的两级式半主动抗冲击座椅悬架概念设计。具体思路为：将座椅悬架系统分为两级，第一级设置带有减振控制策略的磁流变阻尼减振器，用于减小车体传递至人体的振动；第二级设置带有软着陆控制策略的磁流变阻尼减振器，用于缓解座椅受到的垂向强冲击载荷。

1 问题描述

为了研究两级式半主动车辆抗冲击座椅的抗爆性和平顺性，一般需要建立包含车辆轮胎、悬架和车身结构的整车动力学仿真模型。在徐博[13]所建立的9 自由度整车动力学模型基础上，建立了包含4 自由度集中参数人体模型和半主动座椅悬架系统模型的“人体—座椅”动力学仿真模型，并仿真计算了：正弦激励载荷下座椅的有效振幅传递率、随机不平路面激励下的乘员头部加速度响应、半正弦脉冲激励下的乘员头部加速度响应。

通过分析低频正弦波激励下的座椅有效幅值传递率，在频域上评估抗冲击座椅的减振性能；使用随机不平路面激励模拟实际路面激励，以乘员头部加速度均方根值为评价指标，评估座椅悬架在不平路面激励下的减振性能；使用半正弦脉冲激励模拟相同严酷等级的爆炸冲击波载荷，以乘员头部加速度峰值作为评价指标，评估软着陆控制对座椅悬架系统缓冲性能的影响。

2 系统模型建立

2.1 两级式座椅悬架模型

受文献[8]中建立的多级非线性座椅悬架系统设计启发，本文提出了两级式半主动抗冲击座椅悬架系统概念模型。该悬架系统分为独立的2 级，每一级均包含一个弹性元件和一个磁流变阻尼减振器。其中，第1级称为“减振级”，设有线性低刚度弹性元件和以平顺性控制为目标的磁流变减振器，随着车辆行驶而启用，主要用于减小不平路面造成的椅面振动；第2 级为“缓冲级”，设有高刚度弹性元件和以抗爆炸冲击为目标的阻尼减振器；在座椅悬架动行程达到阈值时(座椅面与地板之间相对位移x≥d1)启用，充分利用座椅悬架的大行程、高刚度和可调式阻尼特性，尽可能多地吸收车底的冲击能量，减少传递至人体的载荷，达到乘员“软着陆”的目的。如图1 所示。

图1 两级式半主动抗冲击座椅悬架系统模型

2.2 四自由度人体模型

为了获得不同载荷下的人体响应和量化损伤值，需要建立人体力学模型。集中参数模型能以较低的计算成本快速预测车辆受垂向载荷时人体各部分的动力学响应。本文采用图2 所示的四自由度人体集中参数模型[14]评估座椅的抗冲击和平顺性能。其中：m、k、c、z为质量、刚度、阻尼、位移。该模型包括骨盆、内脏、上身躯干和头部4 部分；各部分之间通过简化的线性刚度和阻尼单元相连；各部分m、k、c参数见表1。根据Newton 第二定律，四自由度人体模型的动力学方程可描述为：

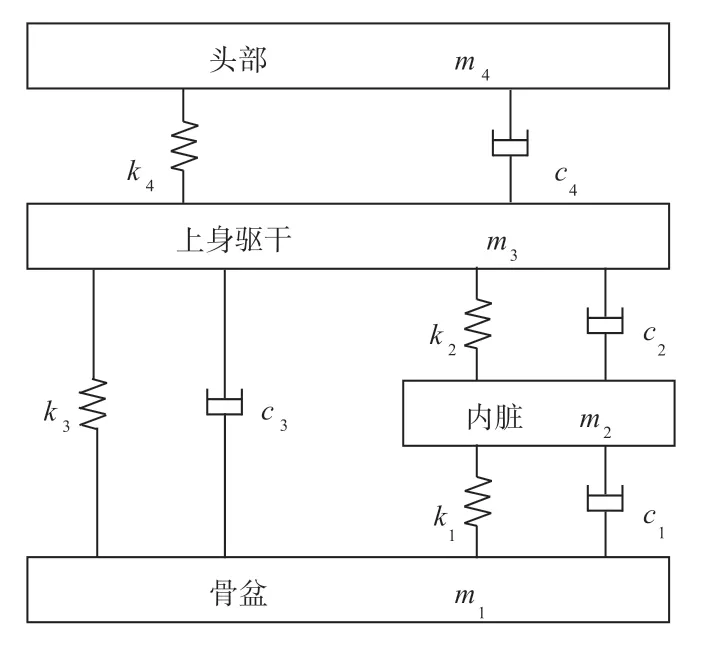
图2 四自由度集中参数人体模型

表1 四自由度人体模型参数[13]

其中，Z= [z1,z2,z3,z4]T为由各部分位移变量组成的位移向量；m、K、C分别代表模型的质量矩阵、刚度系数矩阵、阻尼系数矩阵；F1、F2分别代表座椅悬架产生的弹性力Fk的集合和阻尼力Fc的集合，可表示为：

在垂向载荷作用下，对四自由度人体模型进行验证。根据垂直跌落试验[15]，座椅受到的垂向冲击载荷可近似表达为半正弦加速度脉冲：

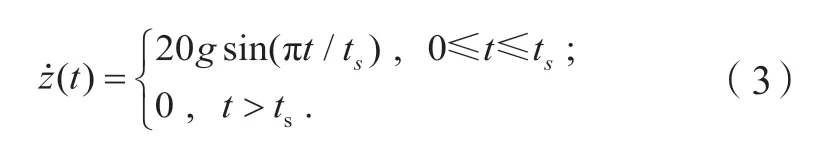
其中，脉冲激励持续时间ts为50 ms。

利用Simulink 建立仿真模型，计算得到冲击载荷下乘员头部加速度时程曲线，可以看出，仿真与实验数据之间存在一定误差，这是由于集中参数模型忽略了乘员坐姿和约束情况。但总体来看，四自由度集中参数人体模型可以较好地预测垂向冲击载荷下乘员头部的动力学响应特性，可用于本文提出的抗冲击座椅悬架系统的性能评估，如图3 所示。

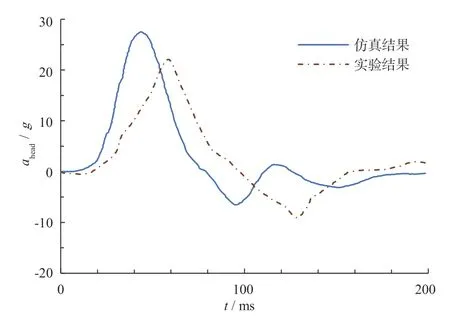
图3 垂向冲击载荷下的人体头部加速度响应

2.3 磁流变阻尼器模型

磁流变阻尼器是一种利用磁流变液的滞回特性实现阻尼力精确控制的新型阻尼器。磁流变液主要优点包括：黏度变化范围大且可逆；响应迅速，易于实现实时控制；工作温度范围宽，稳定性好，可以在-50～150℃正常工作[16]。对阻尼力的精确拟合、预测和跟踪是实现其控制的前提。由于磁流变液的磁滞非线性特性，采用理论推导难以准确全面地描述磁流变阻尼器的力学特性；以激励频率、振幅、速度和控制电流等为输入变量建立参数化模型，进而通过力学特性试验完成参数识别。

综合考虑爆炸冲击载荷对“缓冲级”阻尼力控制精度和计算效率的要求，建立抗冲击座椅悬架磁流变阻尼器的Hysteretic 数学模型[17]。该模型是一种易与控制系统集成的滞后阻尼器模型，由磁滞元件、线性阻尼及线性刚度组成，具有耐温性和响应迅速的特点。此外，该阻尼器建模准确，能成功实现理想的控制性能，其阻尼力可近似表达为：

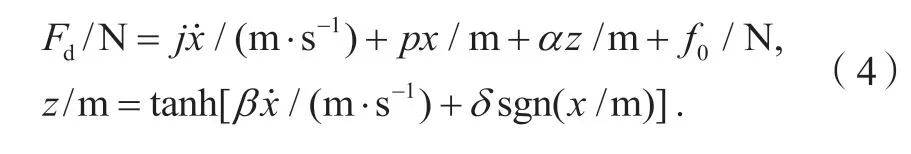
其中：j为阻尼拟合系数，p为刚度拟合系数，α为缩放因子，f0为模型整体的偏置力，δ和β为形状因子。δ取为定值，其余4 个参数为：

磁流变阻尼器外特性试验数据[17]，采用Matlab的lsqnonlin 函数辨识得到不同电流和速度情况下的6个参考值j、p、α、f0、δ、β，利用最小二乘法拟合得到仿真模型参数，如表2 所示。

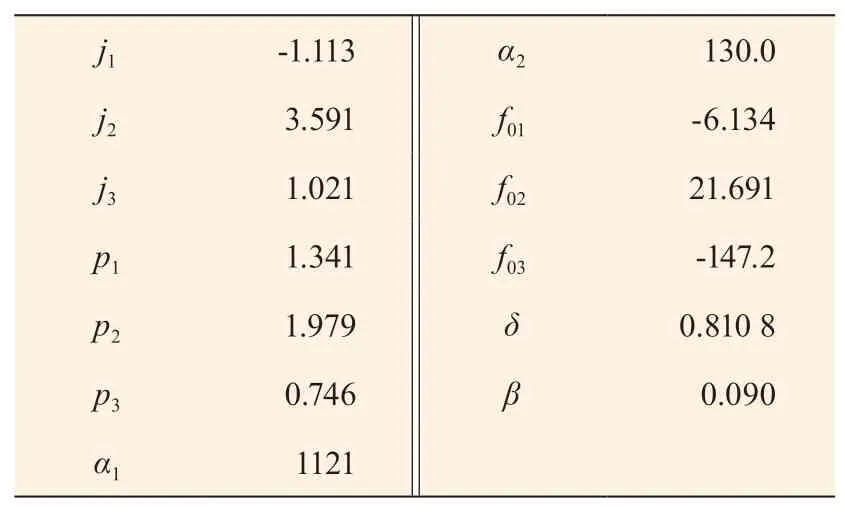
表2 磁流变阻尼器模型参数

为了验证仿真模型精度，将1 A 电流下仿真与试验得到的阻尼器力学特性数据进行对比，可以看出，阻尼器仿真模型最大预测误差不超过5%，满足精度要求，如图4 所示。

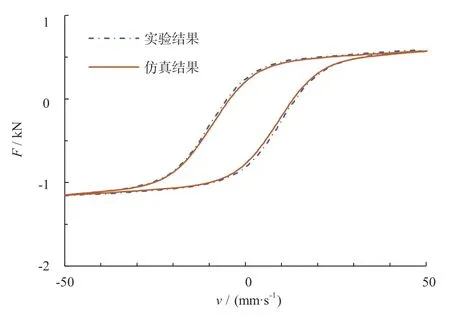
图4 1 A 电流下的磁流变阻尼器力学特性曲线

3 磁流变阻尼控制策略分析

半主动抗冲击座椅悬架系统由悬架骨架、弹性元件、磁流变阻尼器、控制器、电流驱动器以及各类传感器组成。通过安装于座椅面上的传感器实时监测座椅运动状态，由控制器计算得到期望阻尼力，经过磁流变阻尼器逆模型计算得到控制电流，进而通过电流驱动器驱动阻尼器实现阻尼力控制，其工作原理如图5所示。

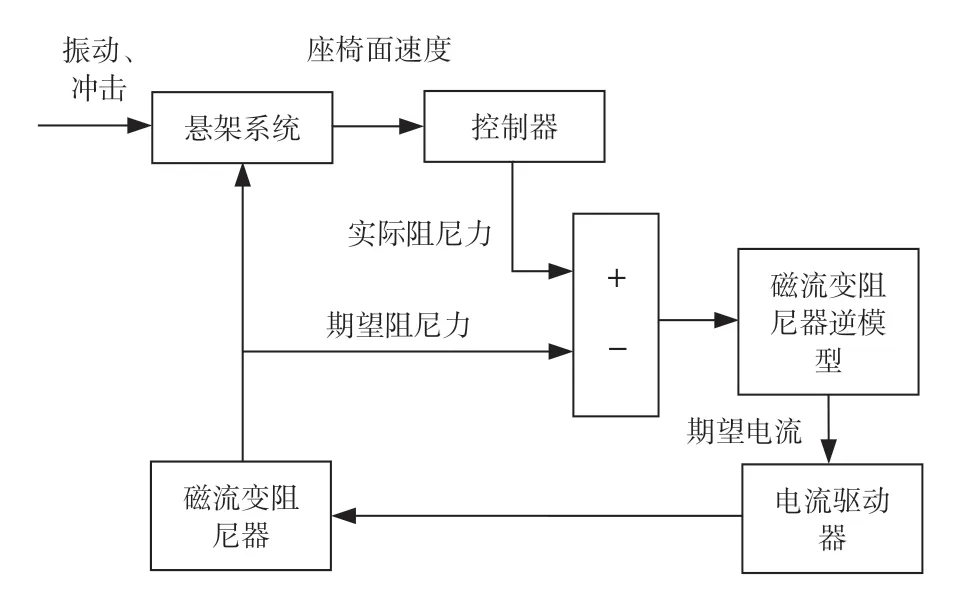
图5 磁流变阻尼力控制原理

在振动控制中，不需要考虑悬架行程对减振效果的影响，减振目标包括： 1) 降低座椅的整体固有频率，以避开人体各部位敏感频率带； 2) 减小驾驶室地板与座椅面之间的振动传递率，以满足舒适性要求。考虑到阻尼器结构的复杂性，且为了满足控制精度和计算速度要求，采用天棚控制和比例 积分 微分算法(proportion integration differentiation, PID)控制作为座椅悬架系统的第一级（即减振级）控制策略。抗冲击控制目标在于充分利用座椅悬架的可变形行程，尽可能多地吸收车底冲击能量，降低对人体的冲击伤害。为此，采用软着陆控制作为座椅悬架系统的第二级 （即缓冲级）控制策略。

3.1 天棚控制策略

天棚控制[18]是目前半主动悬架振动控制的主要策略，核心思想为控制阻尼器开闭以减小座椅面与车体地板之间的相对运动速度，其阻尼力可表示为

其中：żs为车体地板的垂向速度，ż0为座椅面的垂向速度。当座椅面与地板之间的相对速度与地板速度方向相同时，阻尼器开始工作，控制电流取最大值Imax，阻尼力FMR等于天棚控制力Fsky= -żs(żs-ż0)；反之，阻尼器停止工作，控制电流和阻尼力均为零。系统工作时只需在零电流和最大电流之间切换，无需进行复杂的逆模型求解，提高了响应速度。

3.2 PID 控制策略

PID 算法控制在悬架控制中应用较为广泛，PID控制器以座椅面速度与零值的偏差作为反馈，通过控制器计算得到当前座椅运动状态下所期望的阻尼力，并根据阻尼器输出力范围，得到可提供的理想阻尼力，再通过磁流变阻尼器逆模型计算出期望电流，由电流驱动器驱动减振器产生相应的阻尼力以抑制座椅振动。

3.3 软着陆控制策略

Wereley 等人[19]基于单自由度落锤系统，提出了一种能充分利用阻尼器活塞缓冲行程的软着陆控制策略，其核心思想为控制活塞行至行程末端时速度为零，即最大程度地利用阻尼器可用行程，使得落锤以基本恒定的减速度减速至0，达到软着陆的目的。

本文参考落锤冲击缓冲系统，给出“缓冲级”软着陆控制策略的一种具体实现方法。如图6 所示，通过实时采集座椅面与车体地板之间的相对位移zs、相对速度żs以及阻尼器剩余可用行程SMERA，计算得到软着陆所期望的加速度值ad；根据座椅面上一时刻的加速度以及实际输出的阻尼力，计算出系统当前需要的期望阻尼力；经阻尼力跟踪系统计算得到期望励磁电流，最后通过电流驱动器驱动阻尼器产生相应的阻尼力，使座椅面以期望的加速度下落。软着陆控制策略可表达为：

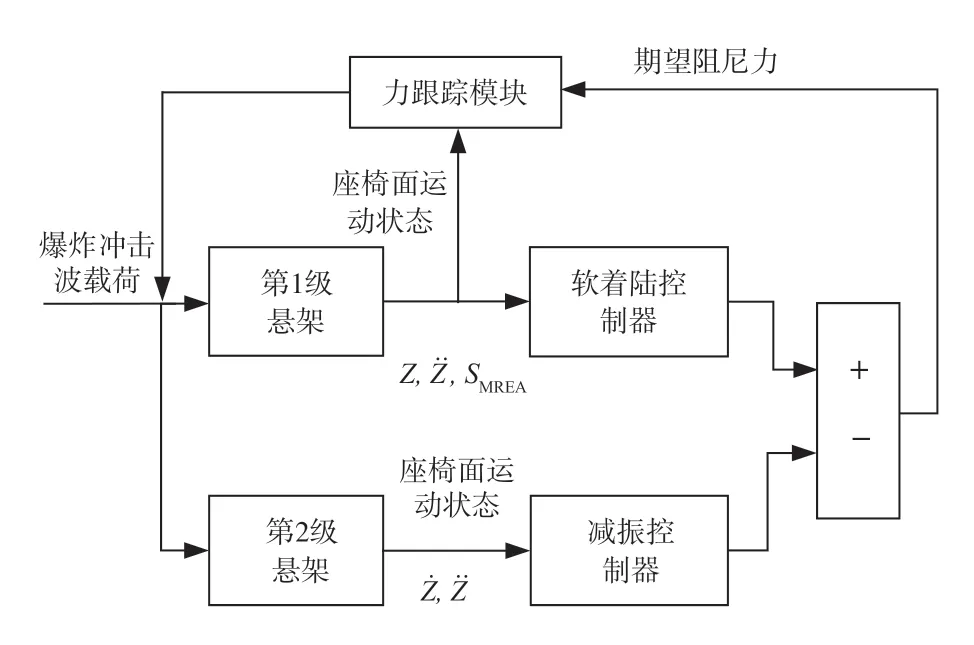
图6 软着陆控制原理

其中： ΔF为期望加速度ad与实际加速度s所需合外力之差；Fexp为控制系统的期望输出阻尼力；Freal为阻尼器实际输出阻尼力。

4 仿真结果分析

4.1 正弦激励载荷下的仿真结果

座椅有效振幅传递率(seat effective amplitude trans missibility, SEAT)是目前座椅减振性能的主要评价指标[20]，其表达式为：

其中：Gxx(f)表示频率f下的座椅面加速度功率谱密度，Gww(f)为频率f下的座椅地板加速度功率密度谱，Wk为标准ISO2631、根据人体对不同频率的敏感程度给出的频率权重。

为了评估座椅有效振幅传递率，基于Simulink 仿真平台，利用人体-座椅模型进行正弦激励载荷下的系统频响分析，频率范围0～10 Hz，频率步长0.25 Hz。仿真获得被动座椅悬架、天棚控制及PID 控制下的座椅有效振幅传递率与输入频率关系如图7 所示。最大有效振幅传递率及其对应的固有频率列于表3。

图7 被动悬架及不同控制策略下座椅有效传递率

表3 3 种悬架的座椅最大有效振幅传递率和固有频率

如图7 所示：高频振动对乘员乘坐舒适性影响不大，3 种座椅悬架的减振效果差别很小；而座椅有效振幅传递率在人体垂向振动敏感频率区间2～4 Hz 内达到峰值，容易产生共振；与被动悬架相比，采用半主动控制悬架的座椅固有频率和有效振幅传递率均有所下降，减振效果更好。其中，天棚控制策略下半主动悬架最大传递率为5.12，相比被动悬架下降了18.7 %；PID 控制策略下半主动悬架最大传递率为5.08，相比被动悬架下降了19.4%。

4.2 路面激励载荷下的仿真结果

车辆正常行驶时受到的路面激励主要源自道路高程的不平度。当车速恒定时，路面不平度服从零均值的Gauss 概率分布，是以时间为参数的随机过程。本文通过随机路面的滤波白噪声建立时速40 km/h下的B 级路面时域模型，其数学表达式为

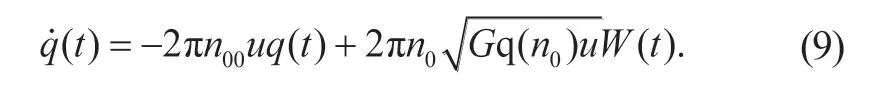
其中，n00为下截止空间频率，取0.011 m-1；Gq(n0)为路面不平度系数，单位为m3；n0为参考空间频率，n0=0.1 m-1；W(t)为均值为零的Gauss 白噪声；q(t)为路面随机高程位移，单位为m。

将车辆以40 km/h 的速度行驶在B 级路面上所产生的振动时域信号作为人体-座椅模型激励信号，仿真得到乘员头部加速度时域响应，如图8a 所示。以10 s内的乘员头部加速度均方根(RMS)值作为评价指标，对3 种座椅悬架的减振效果进行评估；3 种座椅悬架对应的乘员头部加速度RMS 值频域响应fRMS如图8b 所示，其最大值列于表4。

表4 3 种座椅悬架的乘员头部加速度均方根最大值

图8 B 级路面激励下乘员头部加速度仿真结果

仿真结果表明：相比被动悬架，半主动座椅悬架能够大幅度降低共振区频段的乘员头部加速度值，且PID 控制效果要优于天棚控制。在随机B级路面激励下，天棚控制悬架对应的乘员头部加速度RMS 值相比被动悬架下降了32.9%；PID 控制悬架对应的乘员头部加速度RMS 值相比被动悬架下降了35.6%，减振效果更为明显。

4.3 爆炸冲击载荷下的仿真结果

为了评价座椅的抗爆炸冲击性能，美军及北约开展了大量的座椅跌落试验，其载荷可近似表示为峰值200g的半正弦加速度脉冲[21]，相应的数学表达式为：

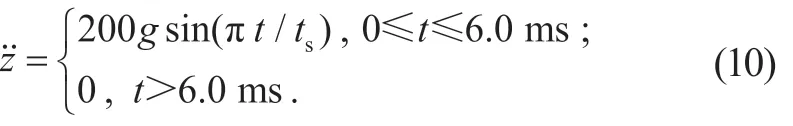
以式(10)表示的爆炸冲击载荷加速度脉冲作为输入，采用本文建立的人体-座椅联合仿真模型，获得被动座椅悬架和采用“软着陆”控制策略的半主动座椅悬架下的人体头部加速度时程曲线对比，如图9 所示。

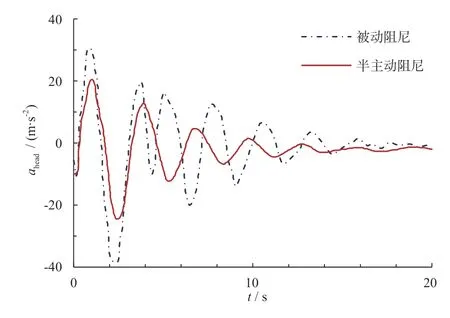
图9 爆炸冲击载荷下乘员头部加速度仿真结果

通过人体头部加速度峰值评估抗冲击座椅的抗爆性。被动座椅悬架下的加速度峰值为40g，两级式半主动座椅悬架加速度峰值为23g，使用半主动座椅悬架头部加速度峰值降低了42.5%。

5 结论

提出了一种面向军用和特种车辆的两级式半主动抗冲击座椅悬架的概念设计，建立了磁流变阻尼器的Hysteretic 力学模型，利用振动测试台测得的阻尼器外特性数据，辨识了模型中对应的系数。基于数值模型，仿真分析了天棚控制和PID 控制下座椅的平顺性和加入软着陆控制后座椅的抗爆性。结果表明：

与被动座椅悬架相比，在标准B 级路面下，加入半主动控制后座椅悬架系统固有频率和加速度均方根值相比被动座椅悬架下降明显，座椅舒适度得到了有效提升；采用软着陆控制策略的半主动座椅悬架系统“缓冲级”能充分利用悬架动行程，有效避免了爆炸载荷下乘员的受伤风险。

此外，两级悬架各自独立，可根据不同需求设计相应的磁流变阻尼器控制策略，具有较大的工程应用潜力。