具有时滞的帕金森模型的振荡动力学分析1)
陈国泰 郑艳红 易 丹 曾巧云
(福建师范大学数学与统计学院,福州 350117)
(福建师范大学福建省分析数学及应用重点实验室,福州 350117)
(福建师范大学福建省应用数学中心,福州 350117)
引言
帕金森病(Parkinson’s disease,PD)是一种神经性大脑疾病,其症状包括静止性震颤、运动迟缓、肌强直和姿势步态障碍等[1-2].据统计,全球约有800 万人患有帕金森病,其中65 岁以上人群的帕金森患病率约为1%~3%[3].我国庞大的人口基数之下,人口老龄化的问题凸显,已知的PD 患者和潜在的患病数给社会带来了一定的挑战.
有研究表明,PD 的主要病理特征是由大脑黑质致密部中多巴胺能神经元的大量退化导致的[4].黑质致密部的变性进一步影响了整个基底神经节—丘脑—皮质(basal ganglia-thalamic-cortex,BGTC)环路的神经元集群活动,特别是基底神经节(BG)中的丘脑底核(subthalamic nucleus,STN)和苍白球(globus pallidus,GP)神经元集群表现出异常同步的β 频段(13~35 Hz)振荡[5].由于病理性的β 振荡动力学的机制尚不明确,因此需要进行更多的研究来探索帕金森病异常β 振荡产生的机制.
国内外许多学者利用神经元模型探索了BGTC环路中产生β 振荡的起源问题[6-11].Holgado 等[12]认为帕金森病的振荡行为起源于STN 与苍白球外侧(globus pallidus externa,GPe)两个神经元集群之间的相互作用.他们通过对系统稳定性进行分岔分析发现当突触连接强度增加时,可诱导STN-GPe 回路中异常同步β 振荡的产生,并发生Hopf 分岔,使系统在健康和帕金森病这两个状态之间转换.Hu 等[13-14]建立了一个两STN 神经元集群的STN-GPe 网络模型,进一步拓展了STN-GPe 神经回路,使得模型更加完善.此外,还有学者认为,除了STN-GPe 环路,在BG 之外的皮质(cortex,CTX)对病理性的β 振荡也具有重要的调节作用[15-19].Pavlides 等[20]基于CTX 和STN-GPe 环路在PD 中产生β 振荡的重要作用,提出了CTX-STN-GPe 模型,其中,皮质分为兴奋性和抑制性两个神经元集群[20],通过此模型成功地重现了Nambu 等[21]的实验结果.另外,突触连接的强度总在神经元活动中起着重要的作用[22-24],例如阻断兴奋性突触传递能够减少神经元的放电活动.有研究表明,帕金森病中多巴胺能神经元的缺失可能会影响树突的兴奋性[25].刘晨[26]基于CTXSTN-GPe 回路建立了一个双振荡神经群模型,探讨了由多巴胺耗尽引起的突触连接的变化对回路中各个神经元集群的影响.
许多学者在研究丘脑底核和苍白球环路时,并未明确区分苍白球外侧(GPe)和苍白球内侧(globus pallidus-interna,GPi),而是将两者视为整体.Plenz等[27]通过观察基底神经节的振荡特性,发现STN,GPe 以及GPi 之间复杂的交互关系能够诱导振荡的产生.GPi 作为基底神经节的输出核团,在皮层和丘脑之间的信号传递过程中发挥着关键的作用,Pavlides 等[20]提出的CTX-STN-GPe 生理学共振模型尚未考虑苍白球内部之间的关联,而仅仅关注了苍白球与其外部神经元集群的联系.因此,本文将GPi 考虑进去,建立更加完善的皮质-丘脑底核-苍白球外侧-苍白球内侧模型(Cortex-STN-GPe-GPi),这更具有生理意义.并在第二节具体研究了与GPi 有关的参数对其产生振荡的影响.该模型有助于对基底神经节重要输出核团GPi 的研究,有助于理解PD 的致病机理.
最近许多学者的研究更进一步强调了突触传输时滞和不同神经元集群之间的突触连接强度会引起异常β 振荡的产生[13,23,28],陈亚倩等[29]通过皮质-基底神经节模型研究了病理性β 振荡的产生与抑制机理,发现突触传输时滞的增加能够导致系统发生超临界Hopf 分岔.此外,研究还发现,不同神经元集群的突触连接强度会引起β 振荡的产生.例如,从STN 到GPe 的强兴奋连接能够诱导GPe 产生β 振荡.以上研究表明,突触传输时滞和不同神经元集群之间的突触连接强度在PD 患者的健康状态和帕金森病状态之间起到了积极的调节作用.
因此,本文主要分为三个部分: 首先,使用突触传递时滞作为分岔参数,通过分岔理论分析了病理性β 振荡的Hopf 分岔产生机制;其次,通过数值模拟阐述了突触传输时滞和突触连接强度能够诱导异常β 振荡的产生;最后,研究与GPi 有关的参数对其产生振荡的影响.希望本文的研究结果能够对帕金森病的治疗方法提供一些参考.
1 模型与方法
1.1 模型描述
基于Pavlides 等[20]提出的CTX-STN-GPe 模型,本文构造了图1 的CTX-STN-GPe-GPi 生理学共振模型.模型由两部分神经回路组成,其中,第一部分为CTX 的兴奋性神经元集群(excitatory pyramidal neuron,E)和抑制性神经元集群(inhibitory pyramidal neurons,I),第二部分为STN-GPe-GPi 组成的神经回路.此外,E 通过神经元轴突将兴奋性谷氨酸能传递到STN 神经元集群,进一步地,STN 将兴奋信号传入GPe 和GPi,同时 STN 还接收到 GPe 的抑制性GABA 能输入.纹状体(striatum,STR) 将抑制性GABA 能传给GPe 和GPi,同时GPi 也接受来自GPe 的抑制信号.
图1 所示的模型由式(1)描述其动力学行为
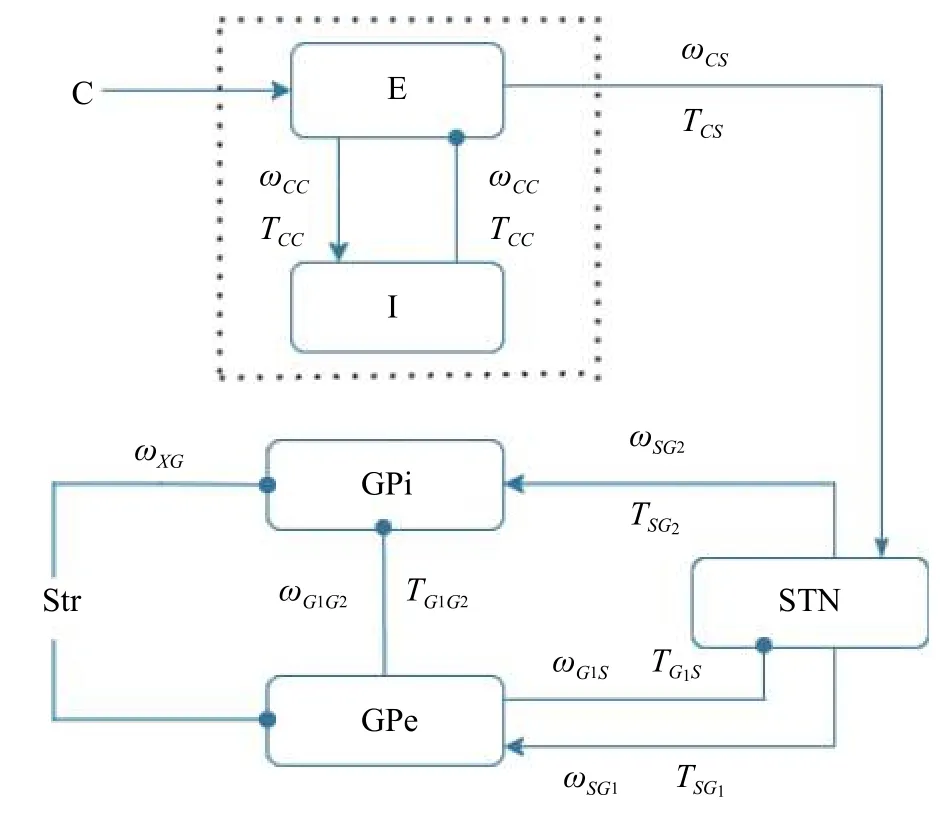
图1 皮质-丘脑底核-苍白球外侧-苍白球内侧共振模型示意图Fig.1 The schematic diagram of Cortex-STN-GPe-GPi
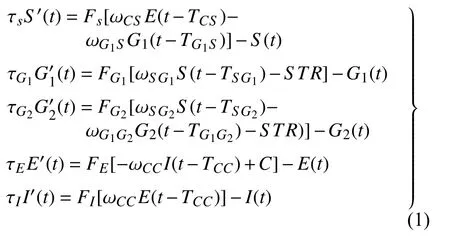
其中S(t),G1(t),G2(t),E(t)和I(t) 分别表示STN,GPe,GPi,皮质兴奋性神经元集群和抑制性神经元集群的放电率.τi(i=S,G1,G2,E,I)表示神经元集群i的膜时间常数.Tij和 ωij分别表示神经元集群i和j之间的突触传递时滞和连接强度.C表示对E 的兴奋性输入常量,STR表示纹状体的外界输入.
FX(X=S,G1,G2,E,I)表示激活函数,满足下式[30]

其中,BX,MX为每个神经元集群的基础放电率和最大放电率.激活函数以及激活函数导数的图像如图2所示.本文中的所有参数,除突触传递时滞和突触连接权重之外,都列在表1 中,更多细节可以在参考文献[20,31-32]中查阅.
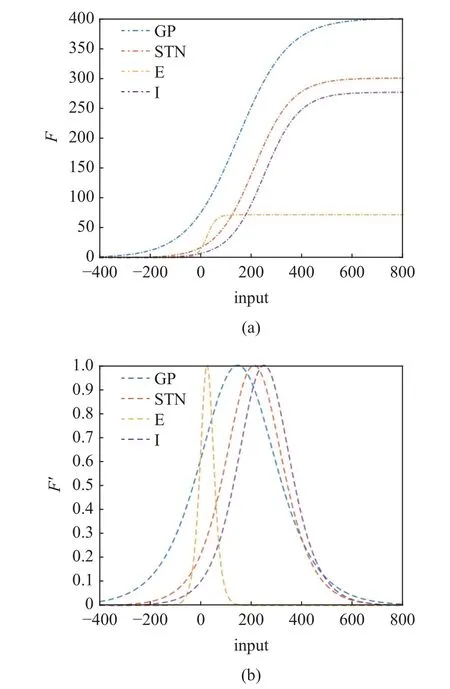
图2 (a) 激活函数曲线图和(b) 激活函数导数曲线图Fig.2 (a) Curves of the activation functions and (b) derivatives curves for activation functions
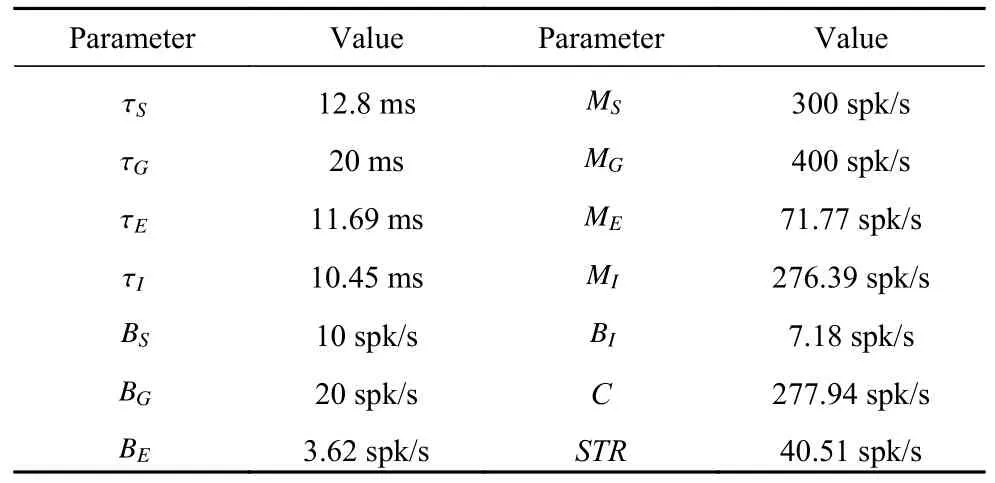
表1 本文参数表Table 1 The parameter values used in this paper
1.2 Hopf 分岔的存在性
由于该模型的复杂性,为了简化,假设膜时间常数和突触传递时滞都相同,记为 τ和T,令 τ=10 ms.因此,可以得到如下动力学公式

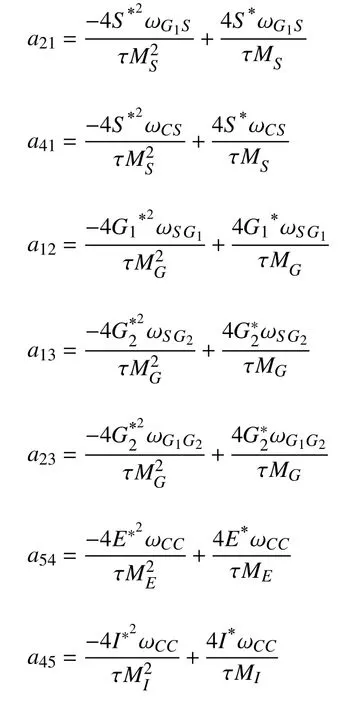
所以系统(3)所对应的特征方程为
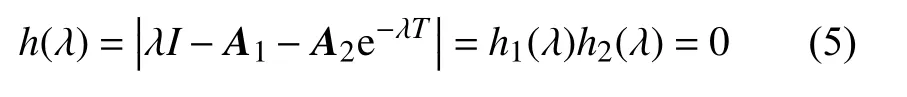
其中
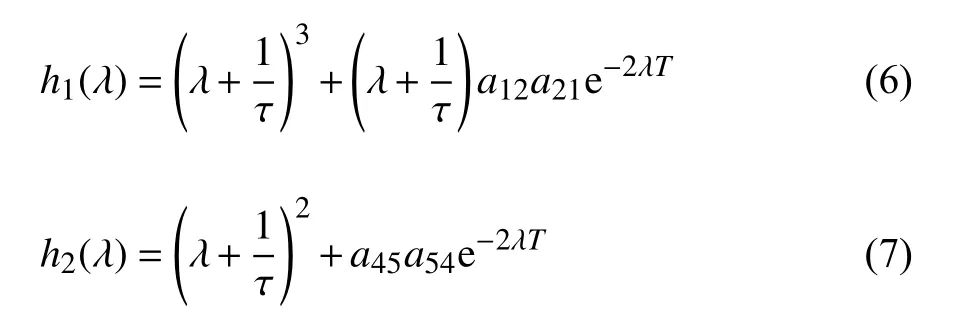
下面根据T值的不同分两种情况讨论.
情形1:T=0
当T=0 时,式(5)可化为
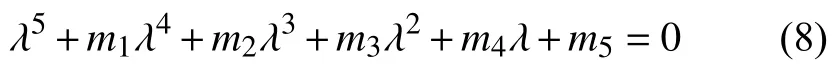
其中
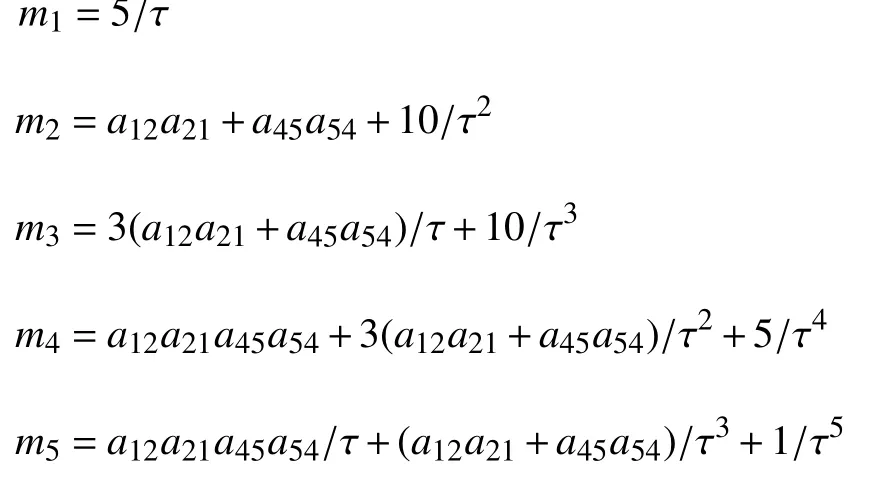
由Routh-Hurwitz 判据[33]可得
定理1.1系统(3)在平衡点P处是局部渐进稳定的,当且仅当式(8)的所有根具有负实部,即式(8)的系数满足下列条件

另一方面,如果式(5) 有一对复共轭纯虚根λ=±iω(ω >0),则系统(3) 在平衡点处的稳定性会发生变化,并在某些条件下会从原点处分岔出一系列小振幅的周期解,即在平衡点处发生了Hopf 分岔现象.因此,需要找出使h1(λ)和h2(λ) 有一对纯虚根的条件.
情形2:T>0
当T>0时,由式(6)可知,h1(λ) 有一个负实根λ=-1/τ,于是转而研究
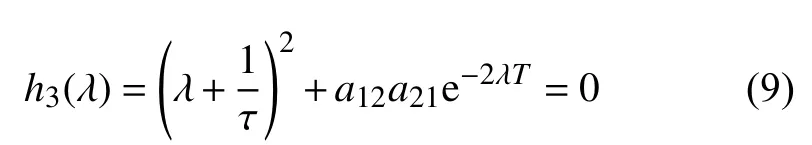
根的情况.(1)假设 λ=iω+(ω+>0)是h3(λ) 的根,可以得到
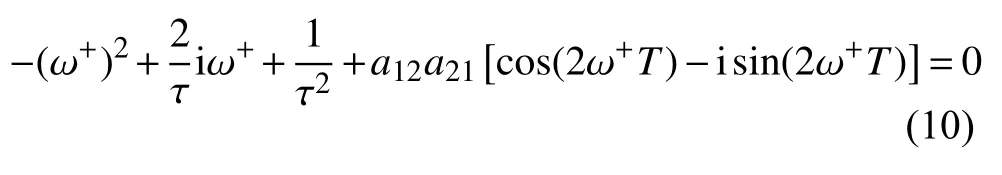
分离式(10)的实部和虚部,有
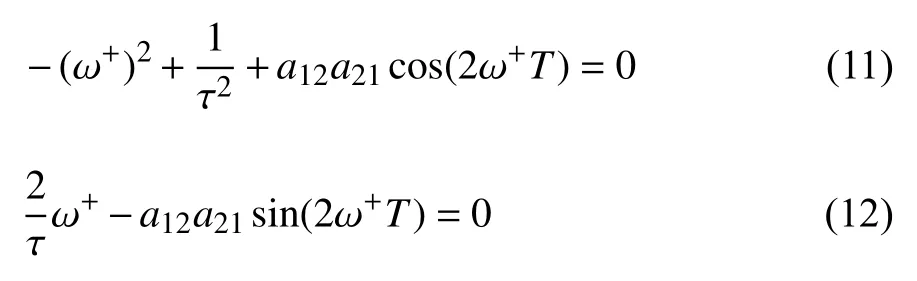
因此,把上述式(11) 和式(12) 的两端平方相加,可得
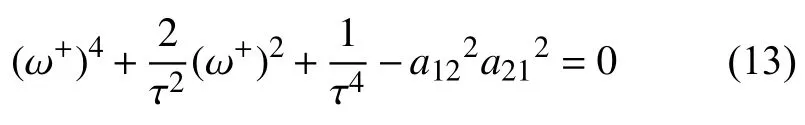
令z=(ω+)2,则
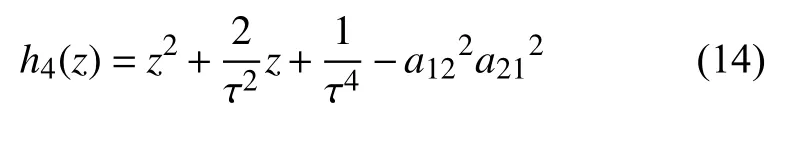
如果条件
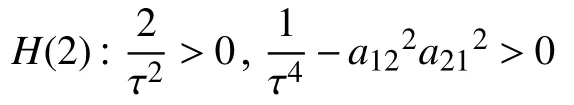
成立,那么式(10)的所有根都具有负实部,因此系统(3)的平衡点 (0,0,0,0,0) 是渐进稳定的.
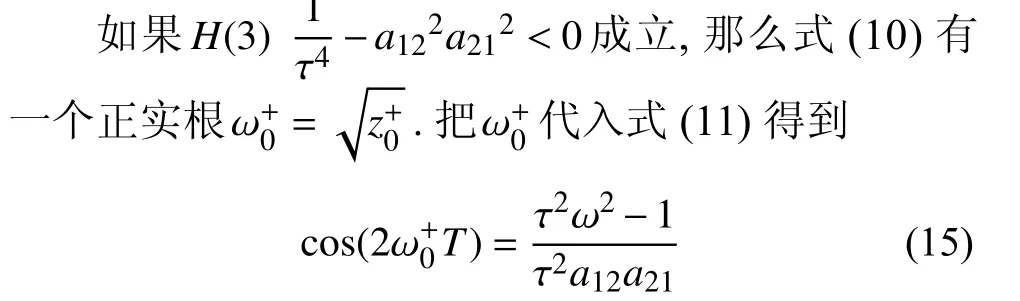
于是
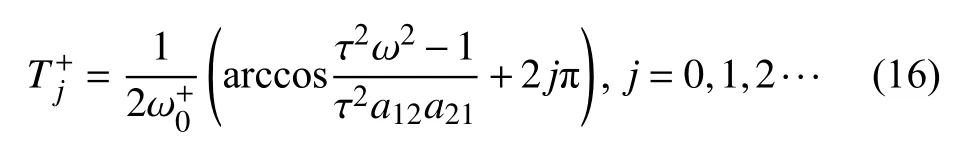
(2) 假设 λ=iω-(ω->0) 是h2(λ) 的根当且仅当λ=iω-满足以下条件
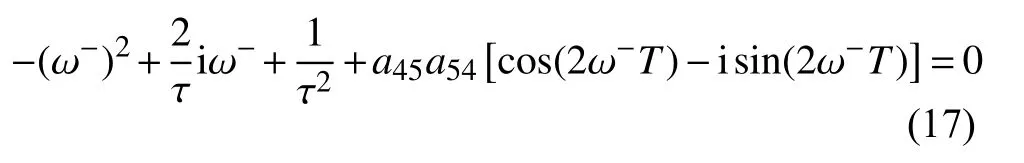
显然,同(1)推导,可以得到

下面,验证相应的横截条件.先对式(9)的两边关于突触传输时滞T求导,有

引理1.1对于超越方程[34-35]
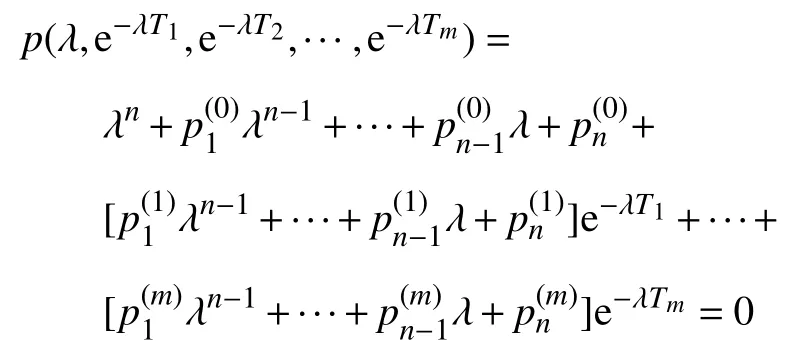
当 (τ1,τ2,···,τm) 变动时,当且仅当有零根出现在虚轴或者穿过虚轴时,在右半平面的零点重数之和才发生变化.
由以上分析以及Ruan 和Wei 的推理[32],可以得到定理1.2.
定理1.2对于系统(3),假设条件H(1),H(3) 和H(4)满足,则如下三条结论成立:
(1)当T<T0时,系统(3)在平衡点P处是渐进稳定的;
(2) 当T=T0时,系统(3) 在平衡点P处产生Hopf 分岔;
(3)当T>T0时,系统(3)在平衡点P处是不稳定的.
2 结果与分析
2.1 突触传输时滞诱导异常beta 振荡
为了阐明突触传输时滞和突触连接强度对帕金森病异常β 振荡产生的影响,本文借助MATLAB软件对模型进行数值模拟.模型中使用的参数均与参考文献[34]一致.即 ωCS=6.6 ,=3.22 ,=2.56,=2.56 ,=0.9 ,ωCC=3.08 .
越来越多的研究表明,突触传输时滞在诱导帕金森病异常β 振荡的产生中起着关键作用[29,36,37]根据1.2 节的分析推导,得到分岔点T0=2.2 ms..
本节对CTX-STN-GPe 生理学共振模型进行了分岔分析并绘制了共振模型放电速率的时间历程图,相图以及STN 放电速率关于传输时滞的分岔图,见图3(a)~图3(d).
图3(a)是关于突触传输时滞的分岔图,其中,蓝色的点线表示稳定的状态,红色的点线表示不稳定的状态.HB 表示Hopf 分岔点.从图中可知,当0 <T<2.2ms 时共振模型表现出唯一的稳定平衡点(对应健康状态),在任何初值状态下STN 的放电速率都收敛于一个恒定的值.当T=2.2 ms 时,共振模型经过HB 点,产生极限环振荡.当T>2.2 ms 时系统出现不稳定的平衡点,产生振荡(对应帕金森病状态).可见,共振模型在T0=2.2 ms 处发生了Hopf 分岔,这与1.2 节的理论结果一致.两种动力学状态所对应时间序列图以及相图,分别见图3(b)~图3(d).在相图中,红色曲线代表健康状态,蓝色曲线代表帕金森病状态.由此可见,改变突触传输时滞,可以诱导异常β 振荡的产生.
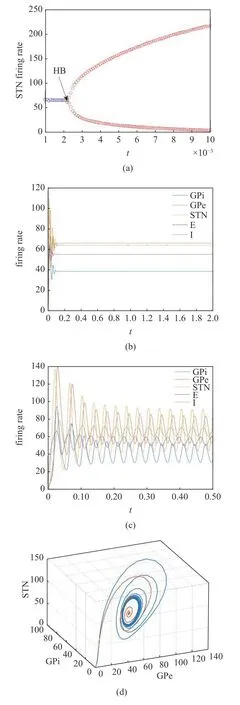
图3 (a) STN 放电速率关于传输时滞的分岔图.共振模型时间历程图: (b) 健康状态,(c)帕金森病状态和(d)共振模型相图Fig.3 (a) Bifurcation diagram of the firing rate of the STN population STN against the transmission delay.Time series of the resonance model:(b) the healthy state,(c) the Parkinson state and (d) phase diagram of the resonance model
2.2 突触连接强度诱导异常beta 振荡
为了研究突触连接强度的改变对异常β 振荡的产生和振荡的振幅的影响,本节分别讨论了突触连接强度 ωCS单独变化对STN 神经元集群动力学行为的影响以及突触连接强度 ωCS和ωG1S同时变化对STN 神经元集群动力学行为的影响.
首先探讨兴奋性神经元集群E 到STN 的兴奋输入连接强度 ωCS对STN 动力学行为的影响.ωCS关于STN 放电速率的分岔图如图4(a)所示,由分岔图可知,当 0<ωCS<80 时,STN 的动力学行为表现为振荡状态,当 ωCS>80 时,STN 从之前的振荡状态转变为单稳态.因此,只要 ωCS在大于0 的参数区域内足够大,可以有效地阻止异常β 振荡的产生.

图4 (a)兴奋性神经元集群对STN 放电率的影响. ωCS和 ωGeS对STN (b) 振幅和 (c)放电率的影响Fig.4 (a) The effect of excitatory pyramidal neuron on STN firing rate.The effect of ωCSand ωG1Son (b) amplitude and (c) firing rate of STN
为了更全面地探讨突触连接强度对STN 产生β 振荡的影响,下面讨论双参数 ωCS和 ωG1S变化下STN 的振幅变化,进而分析 ωCS和 ωG1S的整体改变对STN 动力学行为的影响.图4(b)给出了双参数ωCS和 ωG1S变化对STN 振幅的影响.从图4(b)可以看出,当参数 ωCS和 ωG1S取自蓝色区域时,STN 振荡消失,系统达到健康状态,当参数 ωCS和 ωG1S取在黄色区域内,STN 产生振荡,对应为帕金森病状态,振荡的振幅在黄色区域内较大.为了进一步刻画这种现象,下面分别选取一些典型的参数来模拟STN的动力学行为.当 ωCS与 ωG1S两者的作用逐渐增强时,STN 容易发生振荡,且振幅也逐渐增大.当ωG1S=3.22,ωCS=3 时,系统产生较小的振荡,当ωG1S,ωCS逐渐增加,比如当ωG1S=8,ωCS=35 时,系统产生高振幅的振荡,见图4(c).
2.3 GPi 的相关参数对其振荡的影响
由于GPi 受GPe 突触连接强度和突触传输时滞的共同作用,故本节通过考虑振荡的振幅,来讨论GPe 突触连接强度和突触传输时滞对GPi 振荡的影响.从图5(a)中可以看出,参数区域分为三部分,当参数在A 区域变化时,GPi 振荡,当参数在B 区域时,振荡的振幅减小,而在区域C 时,GPi 振荡的振幅较小甚至消失.因此,当较小的GPe 突触连接强度和较大的突触传输时滞共同作用时,更容易使得GPi 发生振荡,且振幅越来越大.图5(b)为图5(a)对应的时间序列图,以便更简洁明了的通过振幅观察参数对GPi 振荡的影响.从图5(b)可知较小的和较大的会促使GPi 产生振荡.
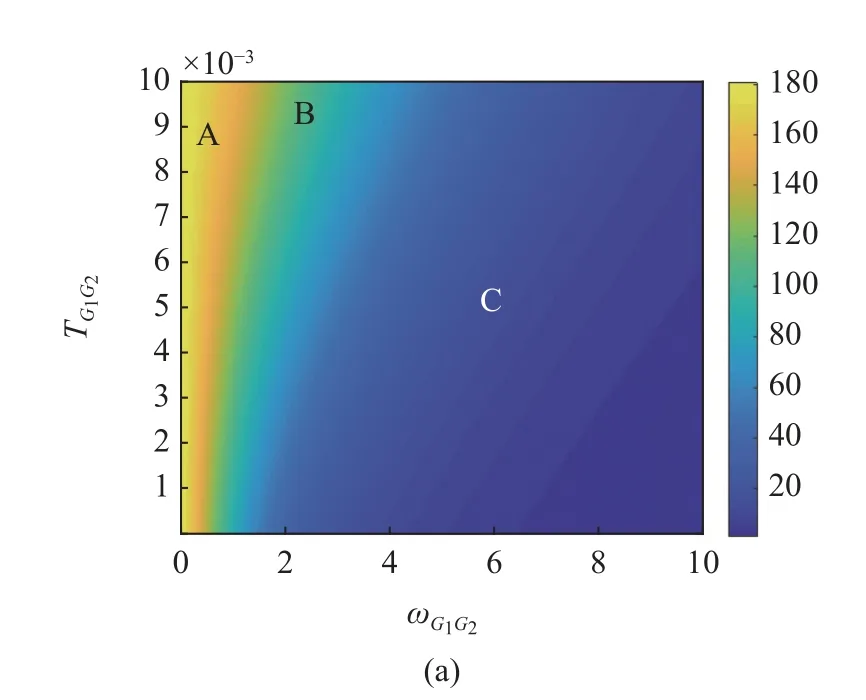
图5 和 对GPi (a)振幅和(b)放电率的影响Fig.5 The effect of and on (a) amplitude and (b) firing rate of GPi
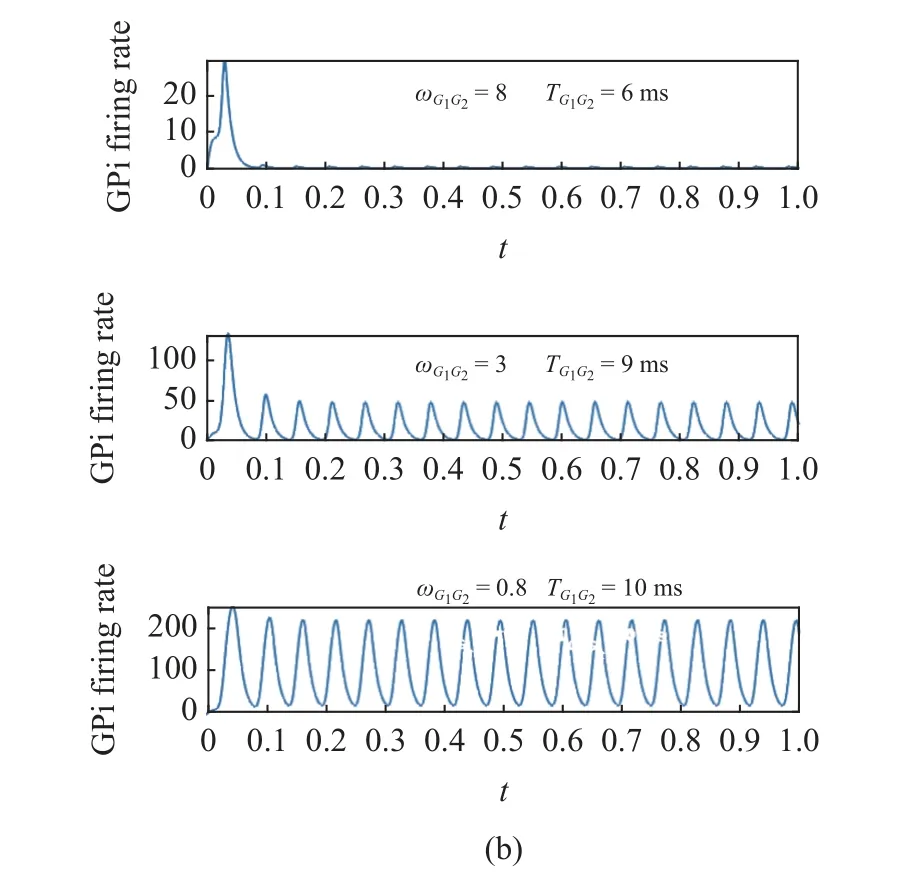
图5 和 对GPi (a)振幅和(b)放电率的影响 (续)Fig.5 The effect of and on (a) amplitude and (b) firing rate of GPi (continued)
3 结论
本文结合PD 相关生理理论,分岔理论,从建模分析的角度出发,对皮质-丘脑底核-苍白球外侧共振模型进行拓展,通过分岔分析和数值模拟揭示了突触传输时滞和突触连接强度对PD 的动力学机制的影响.结果表明,突触传输时滞的增加可以诱导异常β 振荡的产生.其次,发现丘脑底核同时受到兴奋性神经元集群和苍白球外侧较强的促进作用时更容易发生振荡.最后,通过分析β 振荡的振幅对GPi 相关参数的依赖性,发现较小的GPe 突触连接强度和较大的突触传输时滞使得GPi 产生振荡.希望本文的研究结果能够为研究帕金森病的机理提供一些参考.

