两套节点格林元嵌入式离散裂缝模型数值模拟方法1)

程林松 杜旭林 饶 翔 曹仁义 贾 品

* (中国石油大学(北京)石油工程学院,北京 102249)

† (长江大学石油工程学院,武汉 430100)

引言

对非常规裂缝性储层的压力和流体分布进行精确模拟,是许多能源工程技术人员面临的一个热点和挑战性工作[1].目前为止,已有许多数值方法被用于解决这一物理问题,如等效连续介质模型[2]、离散裂缝模型[3]和嵌入式离散裂缝模型(embedded discrete fracture method,EDFM)[4-5].由于具有较高的关键地质特征可视化水平,其中EDFM 的应用最为广泛.但由文献[6-8]所提出的原始EDFM 在计算基质网格与裂缝单元间传导系数的几何因子时,采用了压力与到裂缝面的垂向距离成正比的线性假设,由于非常规储层裂缝与基质的渗透率极差较大,这种理想假设无法准确描述早期的非稳态窜流,会导致一定的误差;此外,原始EDFM 多采用仅适用于矩形网格剖分的有限差分或有限体积法,难以考虑复杂油藏边界,技术应用层面存在局限性.

针对EDFM 早期精度不足、网格适用性不佳的问题,目前国内外有两个主要研究思路: 其一是优化EDFM 网格剖分的前处理算法[9-11];其二是寻求一种更加高效、适用性更强的数值解法.针对基质网格和裂缝单元之间传质量的准确计算问题,由于边界元法相较于有限元法具有半解析精度,可能会是一种较为有效的思路[12].然而,由于实际储层的非均质性极强,原始边界元法无法有效处理这一问题.格林元法(Green element method,GEM)本质上是边界元法的一种变体,在剖分的每个网格中建立边界积分方程,结合了有限元法的变分原理,更适用于解决非均匀介质的非线性问题.原始GEM 由Taigbenus等[13-17]提出,核心思想是将计算域由多边形单元划分,单元顶点被视为未知节点,通过用网格内部压力近似表达式的法向导数估计边界上的法向流量,但仅显式考虑了节点的压力值,因此总体精度不高,误差会随着多边形单元尺寸的减小而增大.后续的学者对原始GEM 进行了改进,Archer 等[18-19]指出,采用较大网格范围内构造的插值基函数能减少原始GEM 的误差;Pecher等[20]和Lorinczi 等[21-24]提出了基于流量向量的格林元法;Taigbenus[25-26]后续发展了修正流量项的GEM,但始终未解决无法显式求解的根本问题;方思冬等[27]结合了混合有限元法和边界元法二者的优势,将压力节点和流量节点设置在网格边的中心点,建立了物理意义明确的混合边界元法;为提高GEM 的鲁棒性,Rao 等[28]提出了模拟格林元法,该方法耦合了模拟有限差分法的核心思想,可满足局部质量守恒,能稳定地求解二阶偏微分方程;Rao 等[29]还提出了两套节点格林元的基本思想,但没有实现与EDFM 的耦合及相关应用.综合上述研究来看,目前大部分格林元法在精度、收敛性及适应的网格类型上各有优劣性,但若要将格林元的优势引入EDFM 的发展中,就必须建立一种同时保持高精度、强鲁棒性且能适用于非结构网格的格林元法.

本文从原始EDFM 的适用局限性出发,利用格林元方法在处理非定常和非均质问题方面具有高精度的独特优势,建立一种能与EDFM 合理匹配的改进格林元法,能精确求解基质与裂缝间的非稳态窜流问题,拓展原始EDFM 技术应用层面的局限性,使其既能求解各类复杂油藏渗流问题,又能使求解结果具有明确的物理意义.

1 格林元法雏形及其局限性

本文研究的是二维孔隙空间中的单相等温渗流问题,流动遵守Darcy 定律,并考虑封闭外边界条件.原始GEM[13]的基本思想是将边界积分方程应用至各个子单元中,离散格式与直接法推导的有限元法较为相似,被广泛应用在如式(1)的二阶偏微分方程中

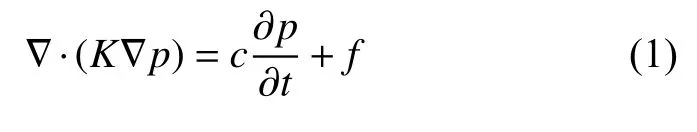
式中,p是计算域内基质的孔隙流体压力,MPa;K和c为渗流介质的属性参数函数,均为标量;f是计算域内的源汇项强度,若渗流介质某基质网格内含有裂缝单元,则有,其中qomf表示该基质网格与裂缝单元间的传质速度,m3/d;V是基质网格体积,m3.

上式可以改写为

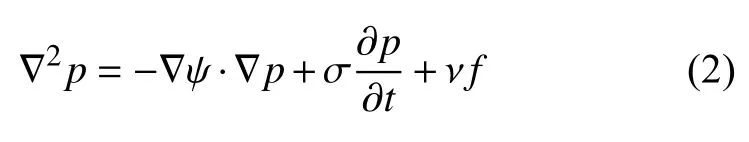
式中,ψ=lnK,ν=1/K,σ=cv.

拉氏方程在无限大计算域的基本解G(M,Mi) 为

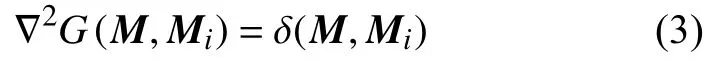
式中,Mi为空间中的源点坐标,M为空间中任意一点的坐标,δ(M,Mi) 为Delta 函数.

根据格林第二公式和式(3),可以得到边界积分方程如下

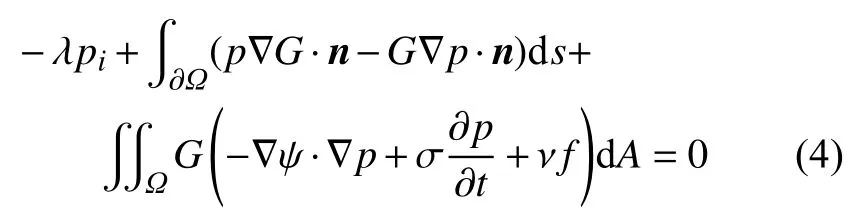
式中,λ 为边界积分方程中所选取源点所处位置的特征角度,Ω和 ∂Ω 分别表示计算域及计算域的边界,n是计算域边界上的外法向量,i是所选取源点的序号.

Taigbenu 等[13-17]利用了法向流量的概念,即令q=-K∇p·n,则上式改写为

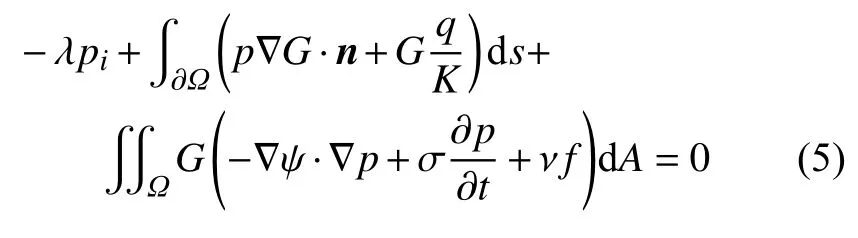
从式(5)可以看出,式中存在与流体压力和介质属性参数有关的域积分,由此体现了GEM 与边界元法的显著差异性,其可以有效处理计算域非均质及参数非线性等更为复杂的问题.以前学者提出过的原始GEM[13-17]、基于流量向量的GEM[21-24]及流量修正的GEM[25],都是在上述GEM 雏形基础上的进一步发展,此类经典方法存在的突出共性问题在于子单元顶点处的外法向流量 (qn=∇p·n) 不具备整体连续性,使得局部物质不守恒.

2 压力流量两套节点格林元法

为此,本文提出了一种压力流量两套节点的改进格林元法,用一组节点包含表示压力值的多边形单元的所有顶点作为压力节点;用另一组包含表示法向流量值的网格边的中心点作为流量节点.其中心思想是通过将流量节点设置在网格边的中点,并作为常单元,以此满足局部物质守恒.该方法可适用于任意形状的网格剖分,下述推导以三角形网格为例,如图1 所示,改进的格林元法具有压力和流量两套不同节点,其中压力节点分布在三角形单元的三个顶点,流量节点分布在三角形单元三条边的中心点.压力节点分别标记为1,2,3,流量节点分别标记为a,b,c.

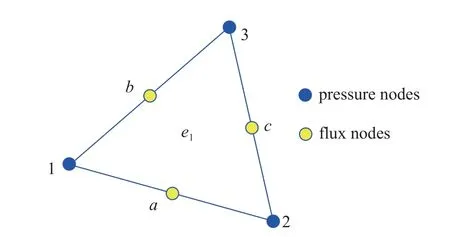
图1 压力和流量两套节点三角形单元示意图Fig.1 Sketch of pressure and flux two sets of nodes in triangle cell

对三角形单元获取如式(4)的边界积分方程,其包含有与压力有关的积分项,需对压力节点值进行插值来估计压力函数在整个单元上的取值,通常压力节点仍然选择在多边形网格的顶点,以保证插值函数之和在整个单元内的取值均为1.每个压力节点相应的基函数表示为 φi,三角形单元内的压力值可由节点值和基函数的加权平均得到,即

但对于每个流量节点,可根据法向流量的分段连续性,将网格边上的法向通量视为一个常量,这是与原始格林元法截然不同的地方.流量节点所在的边记作Γz(z=a,b,c),按上述思想,式(4)的离散格式为

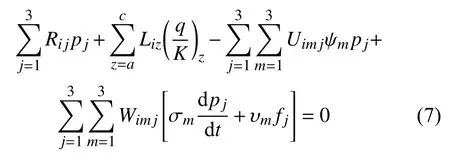
式中

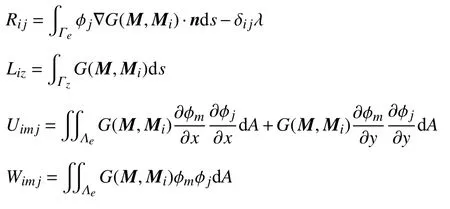
则单元内的局部方程组的矩阵形式为

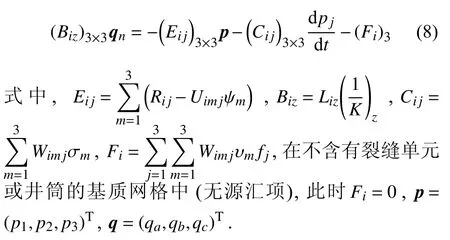
计算矩阵B的逆矩阵,将上式变形为

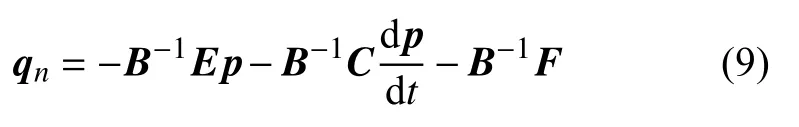
利用权重系数θ控制显隐式程度,得到

简写为

式中

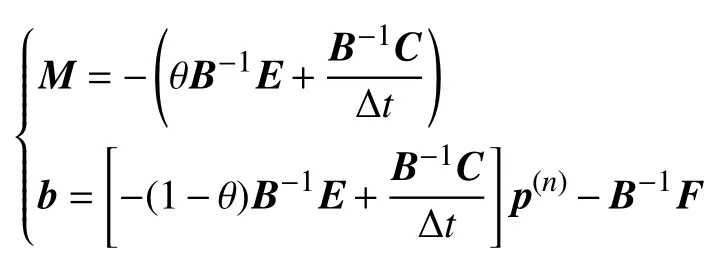
3 改进格林元法与EDFM 的耦合求解

基质与裂缝之间的窜流量被认为是基质单元中的源项或汇项,因此有必要明确哪个单元中存在源项或汇项,而这和基质与裂缝之间的几何性质有关.本文所提出的改进格林元法可适用于任意单元类型的网格剖分,如矩形单元和三角形单元,其中三角形单元的前处理,本文借助了开源程序Distmesh 三角形非结构化网格剖分的Matlab 代码[30-31].相比于矩形结构化网格,三角形非结构化网格没有规则的拓扑结构,网格节点的分布更具灵活性,在诸多工程力学领域均有较好的应用[32-33].如图2 所示的二维EDFM,其中两条离散裂缝分别以红色和绿色的线段绘制,通过基质单元的网格边界将与其相交的裂缝离散为多个裂缝单元,并对每个裂缝单元进行编号.

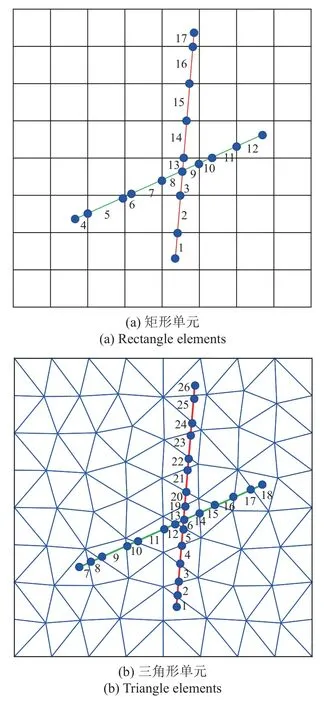
图2 基于改进格林元法的二维EDFMFig.2 Two-dimensional EDFM based on the modified GEM

针对渗流介质某基质网格内含有裂缝单元的情况,可将源点取在裂缝网格中心,由于该点是基质网格内点,其特征角度为2π,则得到相应的边界积分方程离散格式如下

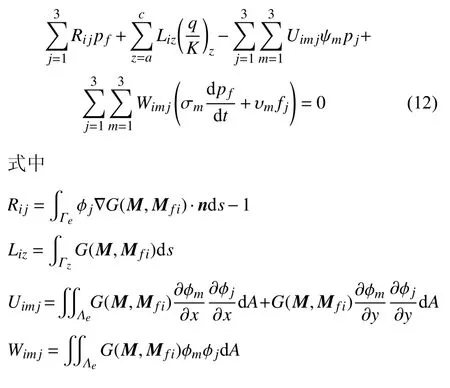
此时Mfi是裂缝网格中心坐标.将式(12) 变形后,得到

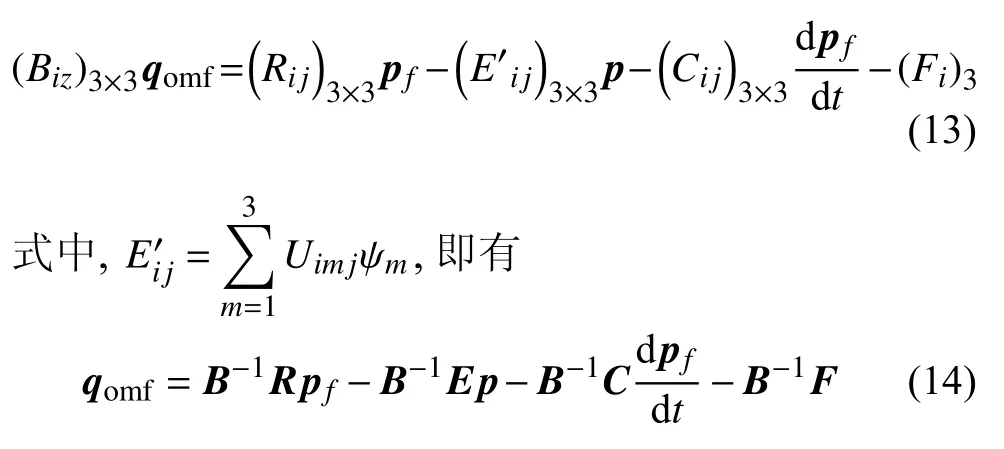
式(14)即为考虑压力瞬态效应的基质网格与裂缝单元之间的传质表达式,式中B-1,R,E,C仅仅与基质网格和裂缝单元的几何参数有关,表征了裂缝单元分布在基质网格中的几何特征.与传统线性分布假设不同,该表达式中除了包含基质孔隙压力和裂缝孔隙压力,还包含了裂缝孔隙压力对时间的导数项,即体现了裂缝孔隙压力的瞬时变化率.因此,相较于传统两点线性流量估计格式,可提高针对低渗透/致密储层中由于基质与裂缝两者间渗透率差异极大所产生的早期非稳态窜流量的数值计算精度.

对于相邻的基质网格,存在连续性条件: 共有的压力节点具有相同的压力,共有的流量节点处的流量相同,即两个相邻基质网格在共有流量节点处的外法线流量的代数和等于0,这也是两套节点格林元法的基本原理.如图3 所示,以两个相邻三角形基质单元为例,介绍耦合过程的细节.

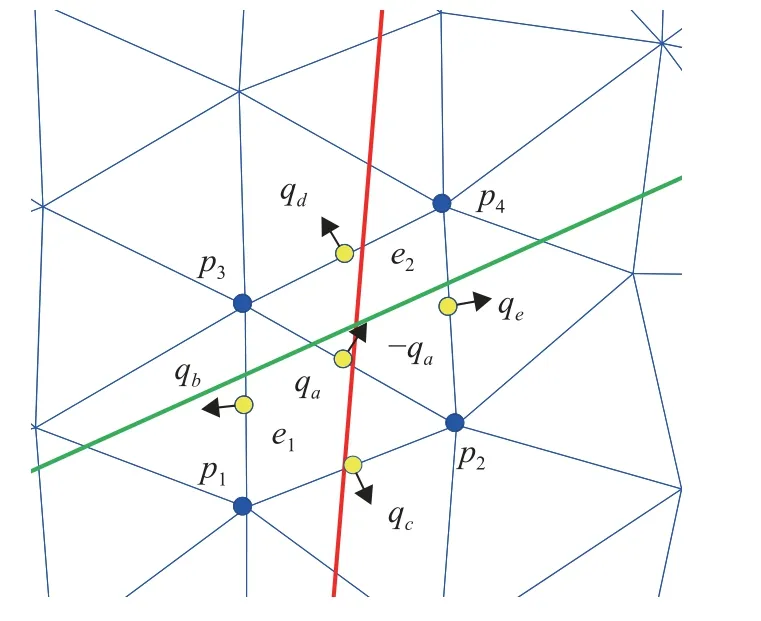
图3 两套节点格林元方法中相邻单元方程组耦合示意图Fig.3 Sketch of coupling adjacent element equations in two sets of nodes-based GEM

假设基质单元e1内的方程组为

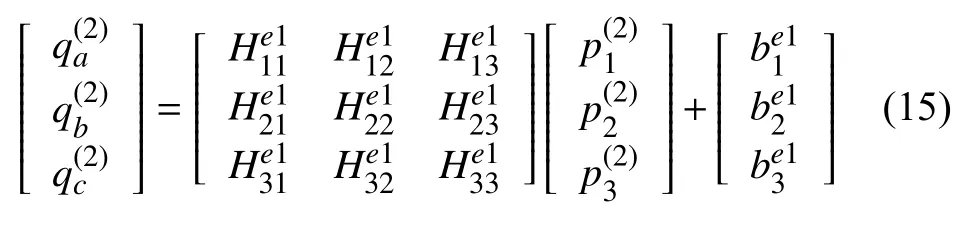
单元e2内的方程组为

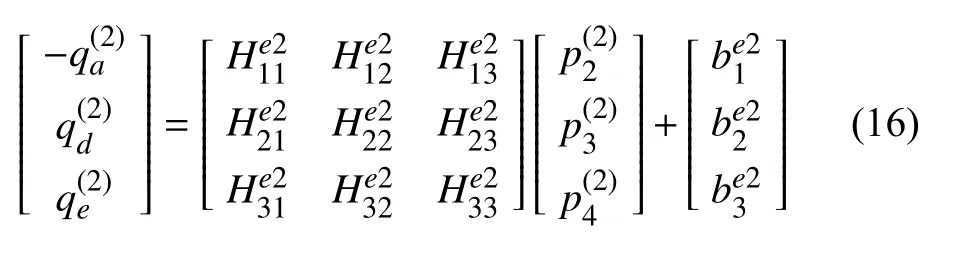
则两个相邻基质单元方程组耦合为

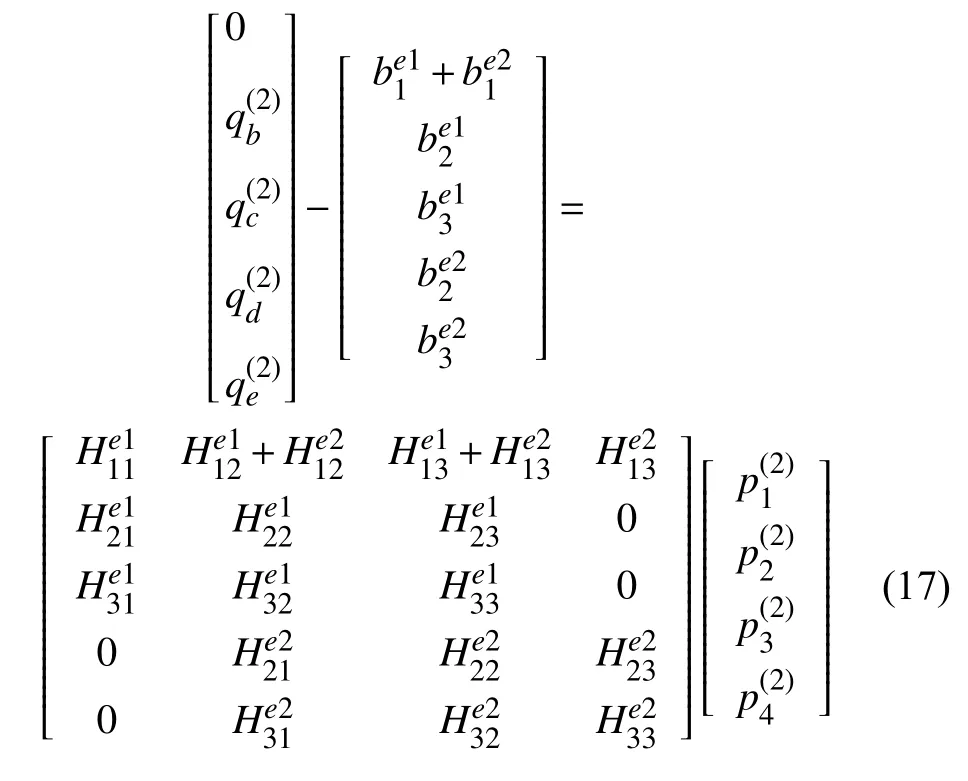
此外,对于离散裂缝网络中的流体流动问题,可采用有限差分法对流动方程进行离散.如图4 所示,单条裂缝可离散成多个裂缝单元,离散裂缝交汇处的流量交换可采用星三角变换方法[34-35]进行处理.

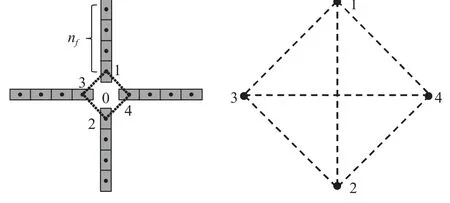
图4 裂缝交汇的星三角变换原理图Fig.4 Schematics of star-delta transformation for fracture segments intersecting

得到相应的有限差分隐式格式,共nf个方程

假设基质单元节点数为np、基质单元边的个数为ned、裂缝单元的个数为nf.由此可知,全局方程组由两部分构成: 一部分是基于式(11),采用式(17)耦合方法获取的表征基质网格间渗流的方程组;第二部分是由式(18)构成的表征裂缝网格间流动的方程组,且这两部分方程组中的qomf用式(14)表示.

整体上,全局方程组共有ne+nf个方程(其中第一部分方程有ne个,第二部分方程有nf个) 和np+nf个未知量(包含np个基质网格节点压力和nf个来源于裂缝单元的未知量).因为ne大于np,可得知由改进格林元法获得的该全局方程组为超定方程组,在封闭外边界条件下,此时方程组可表示为

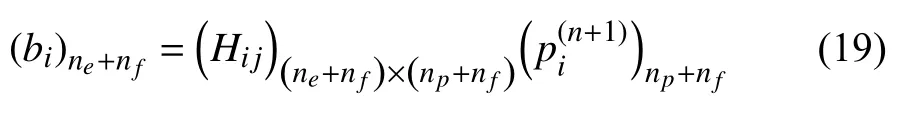
基于泛函分析中的正交投影定理,该超定方程组的解可等价于计算式(20)的解.由此,所有的未知量均可获得.

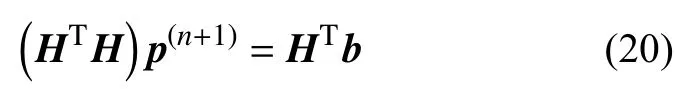
4 模型验证及讨论

4.1 模型验证

将本文提出的两套节点格林元法EDFM 与原始EDFM[6]及商业模拟软件tNavigator®LGR 模块进行对比,其中tNavigator®是由俄罗斯Rock Flow Dynamics (RFD)公司开发的高性能商业模拟软件,其结果可以参考为精确解.该实例是采用单水平井和单压裂缝的机理模型验证本文模型对长期产能预测的准确性,低渗透储层物性参数值见表1.图5 展示了矩形储层域的示意图,地层中心有一口生产井和一条压裂210 m 的主裂缝,水平井筒穿过裂缝中点.对储层域进行离散化,tNavigator®LGR 模块局部加密网格处理的裂缝必须沿网格线方向展布,而在EDFM 中裂缝走向不受限制.水平井采用10 MPa 恒定井底流压制度进行生产,图6 展示了三种不同模型计算1000 天的压力分布场图,图7展示了三种不同模型所获得的日产油量曲线.结果表明,三种不同模型的结果吻合较好,验证了该方法对产能预测的整体精度.

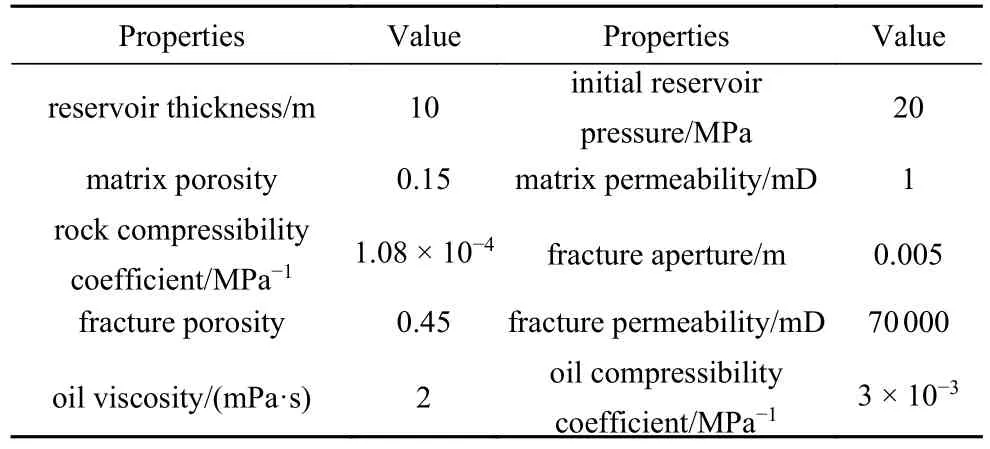
表1 数值算例的输入参数Table 1 Input parameters of numerical case

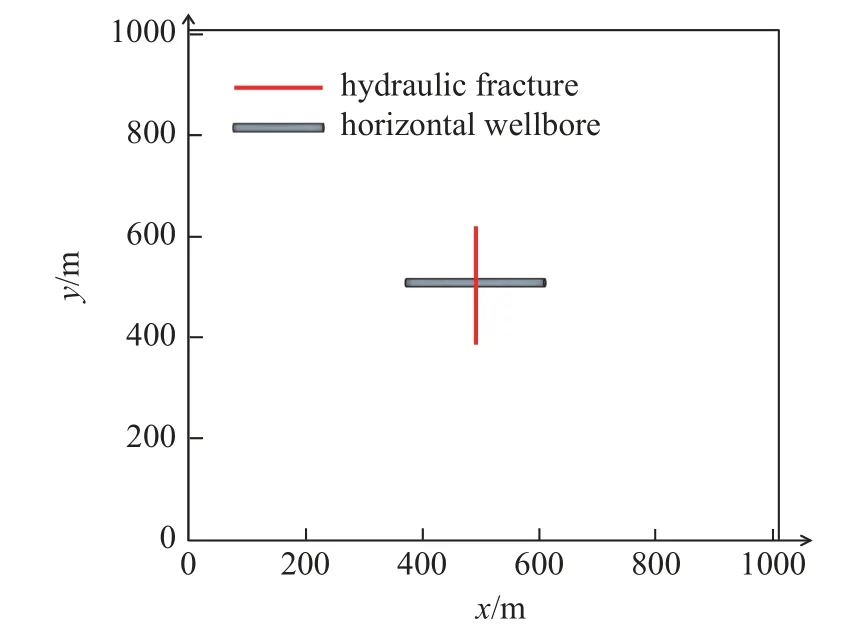
图5 压裂水平井示意图Fig.5 Sketch of fractured horizontal well

图6 三种不同模型压力分布对比图(1000 d)Fig.6 Comparison of pressure distribution maps for three various simulators (1000 d)

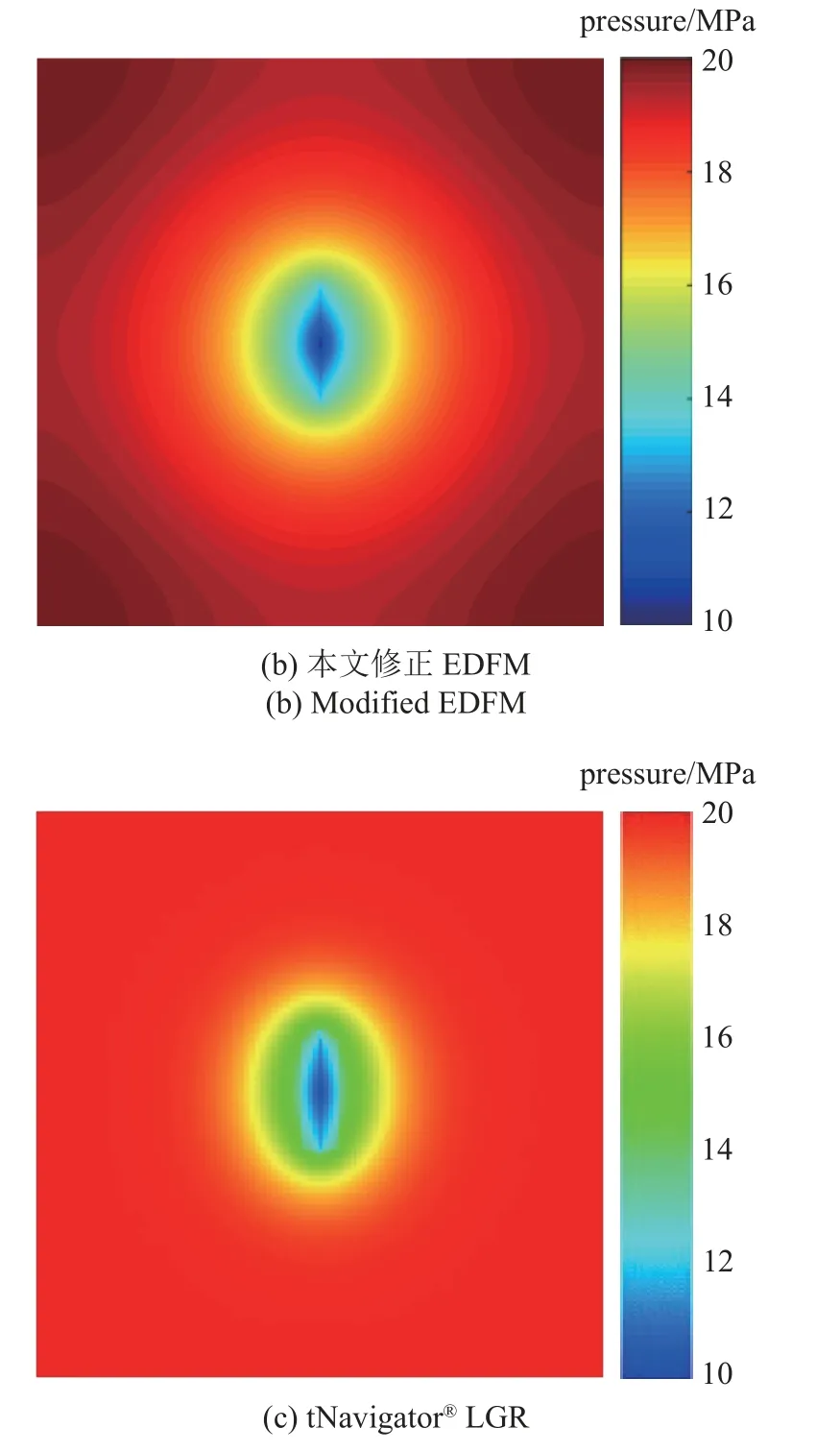
图6 三种不同模型压力分布对比图(1000 d)(续)Fig.6 Comparison of pressure distribution maps for three various simulators (1000 d) (continued)

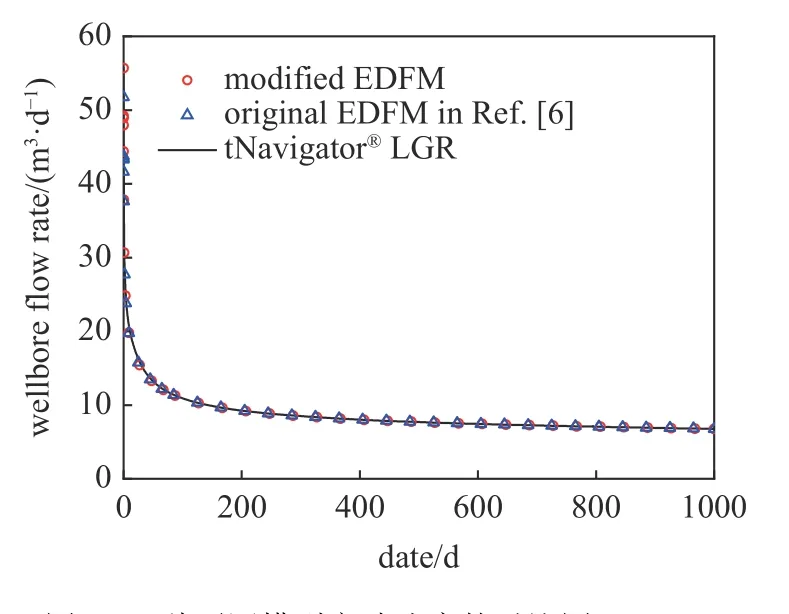
图7 三种不同模型产油速度的对比图(1000 d)Fig.7 Comparison of oil rate for three various simulators (1000 d)

4.2 基质-裂缝间瞬态流动对比

该算例旨在验证两套节点格林元法EDFM 能够较好地反映基质-裂缝间的瞬态流动,算例的基本属性与表1 中的参数值相同,讨论中考虑了两个重要因素: 网格大小和基质渗透率,将网格尺寸设置为2 m × 2 m 和10 m × 10 m,基质渗透率分别为0.1 mD,1 mD 和10 mD.计算时间设置为10 d.为了实现对早期瞬态流动的准确描述,与上一个算例相比,在模拟过程中使用了更小的时间步长.图8 展示了三种模型(网格步长10 m × 10 m)模拟10 d 压力分布的比较,从压力场的结果来看,不同模型之间没有显著差异.图9 比较了在不同网格尺寸(2 m ×2 m 和10 m × 10 m)和基质渗透率(0.1 mD,1 mD,10 mD) 条件下,由三种模型(原始EDFM、本文EDFM 和tNavigator®)计算所得的日产油量曲线.与tNavigator®结果相比,从生产早期可以明显看出,本文EDFM比原始EDFM 具有更高的精度,这是因为本文提出的两套节点格林元法能够有效地反映局部基质网格和裂缝单元之间的瞬态流动,取代了原始EDFM 的线性流动假设,瞬态效应的程度与网格尺寸和基质渗透率密切相关.平均相对误差可由式(21) 获得,计算结果如图10 所示.结果表明,本文EDFM 的平均相对误差比原始EDFM 小得多.同时,随着基质渗透率的降低和网格尺寸的增大,瞬态效应的影响增大,平均相对误差增大.本文所提出的两套节点格林元法实现了对基质-裂缝间瞬态流动更准确的表征,能提高模拟的早期精度.

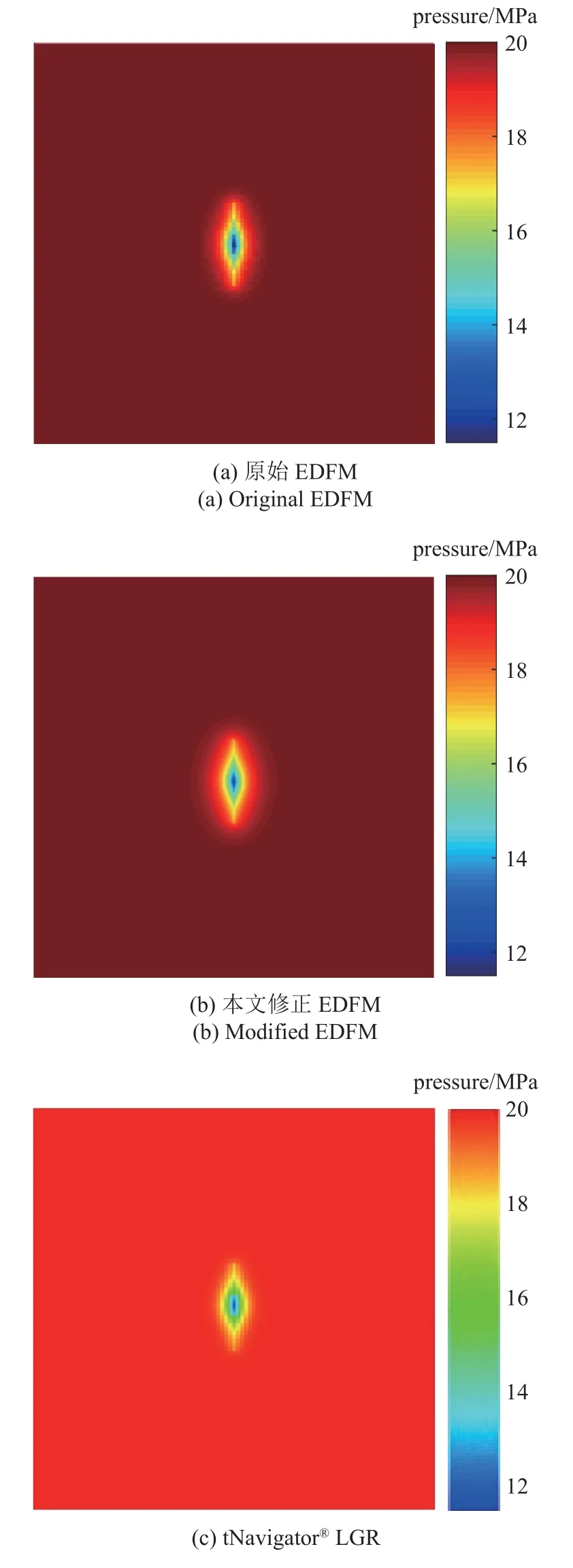
图8 三种不同模型压力分布对比图(10 d)Fig.8 Comparison of pressure distribution maps for three various simulators (10 d)

图9 井筒流量早期结果对比Fig.9 Comparison of early-time results for wellbore flow rate

图10 原始EDFM 和修正EDFM 之间的误差比较Fig.10 Error comparison between the original EDFM and themodified EDFM

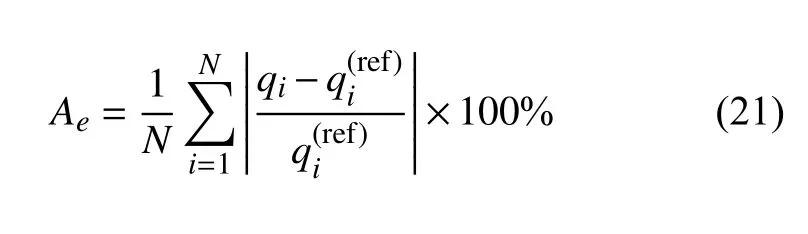
式中,qi表示由EDFM 计算所得的井筒流量,m3/d;为由tNavigator®计算所得的井筒流量,m3/d;N为时间步数.

4.3 复杂油藏边界-缝网-SRV 分区模型

原始EDFM 仅支持矩形结构化网格剖分,在网格适用性方面存在局限性.由于格林元法的引入,本文改进后的EDFM 可支持非匹配性的非结构化网格剖分,能较完善地考虑复杂油藏边界-缝网及SRV 分区的非常规油气储层体积压裂井产量分析的复杂问题.本算例考虑基质渗透率为0.1 mD 的致密储层,人工裂缝渗透率为5000 mD,其他参数值同表1,图11(a)展示了储层域的基本模型,图11(b)和图11(c) 分别考虑了圆形和矩形的SRV 改造区.COMSOL 商业模拟软件以标准有限元(SFEM)为基础,对DFM 的模块化处理极为成熟.本文以SFEMCOMSOL 数值解为参考,以图11(a)中的基本模型为例,对本文模型进行验证,不同模型的网格剖分对比见图12.水平井采用10 MPa 恒定井底流压制度进行生产,图13 对比了本文模型与SFEM-COMSOL两种模型模拟1000 d 的日产油量曲线,结果对比本文模型的解与参考解较为吻合,验证了本文模型在考虑复杂油藏边界条件下产量预测的准确性.

图11 储层域示意图Fig.11 Sketch of reservoir domain

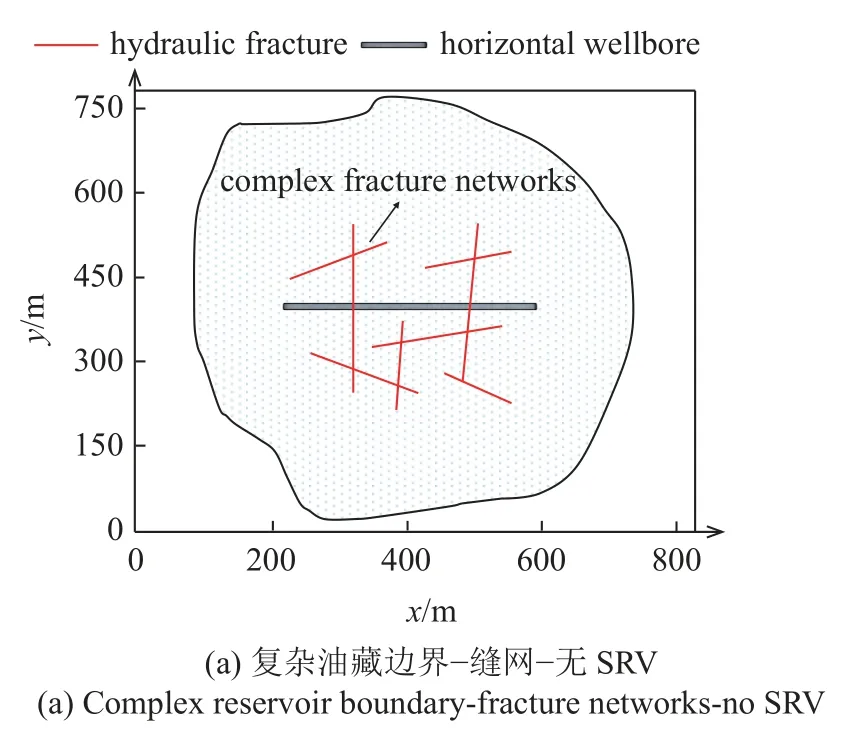
图12 不同模型的网格剖分对比图(续)Fig.12 Comparison diagram of mesh division for different simulators (continued)

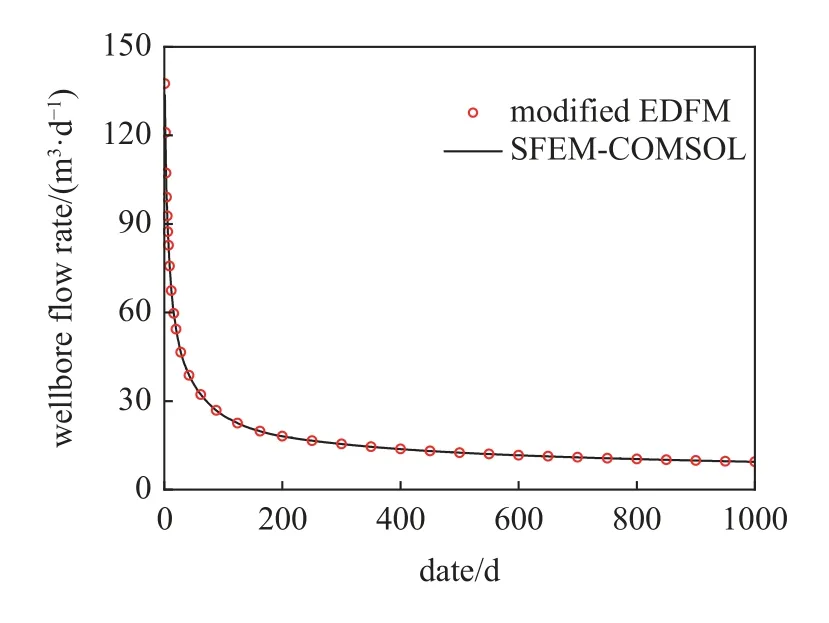
图13 修正EDFM 与COMSOL 产油速度的对比图(1000 d)Fig.13 Comparison of oil rate between modified EDFM and COMSOL (1000 d)

图14 展示了本文模型对图11(a)的基本模型不同开发阶段得到的压力分布情况.图15 展示了本文模型对图11(b)和图11(c)两种不同SRV 分区模拟100 天的压力分布对比,从图中能看出开发早期以缝网内部流体流动为主,生产井产量完全由裂缝供给;当考虑SRV 分区时,开发中期离散裂缝周围的内区流体以垂直于裂缝面的方向流入裂缝,由于内外区基质渗透率级别存在差异,开发后期压力波才慢慢向外区传播.本文所提出的方法采用非稳态渗流控制方程的边界积分形式推导了基质网格与裂缝网格之间传质量的新格式,因此也可以将EDFM 的适用性拓展至油藏压裂井早期生产动态特征分析.图16 对比了不考虑分区、矩形SRV 和圆形SRV三种SRV 形态的生产动态特征,其中矩形SRV 对应的外区流动形态为复合线性流,圆形SRV 对应的为拟径向流,不考虑分区的产量动态特征位于二者之间.

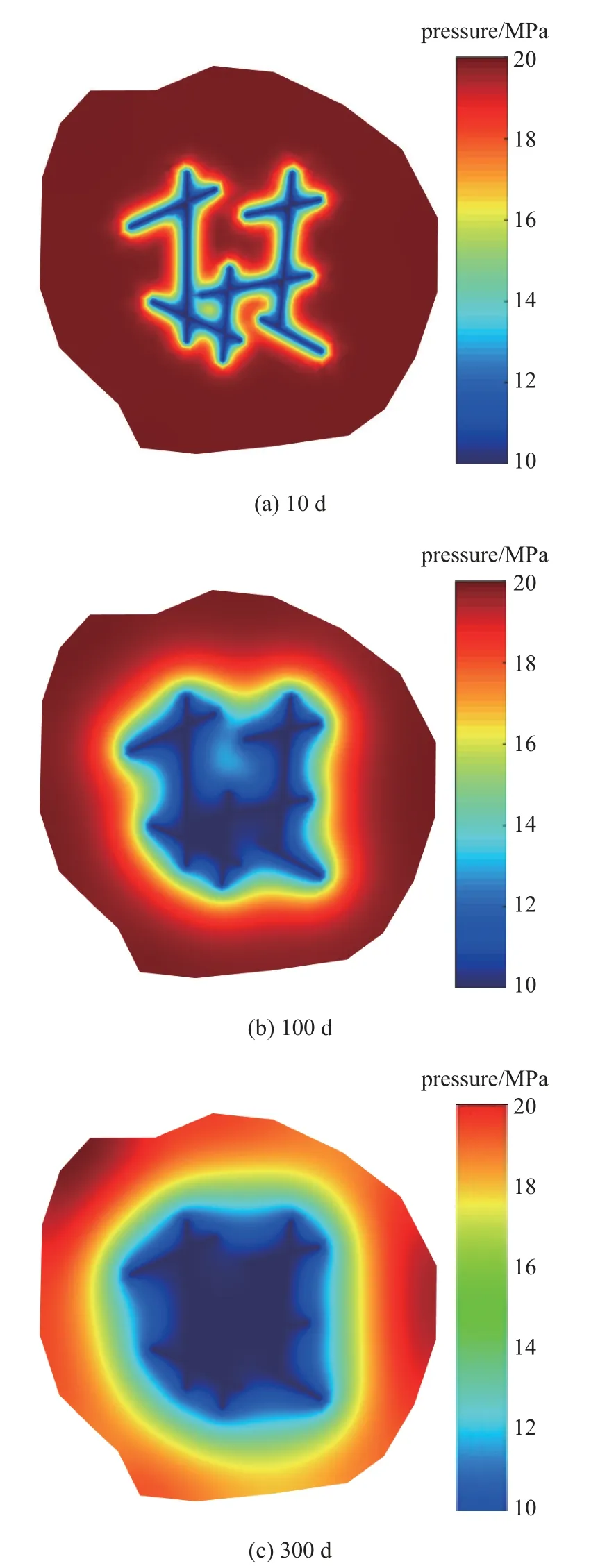
图14 基础模型压力分布场图Fig.14 Diagram of pressure distribution field for basic model

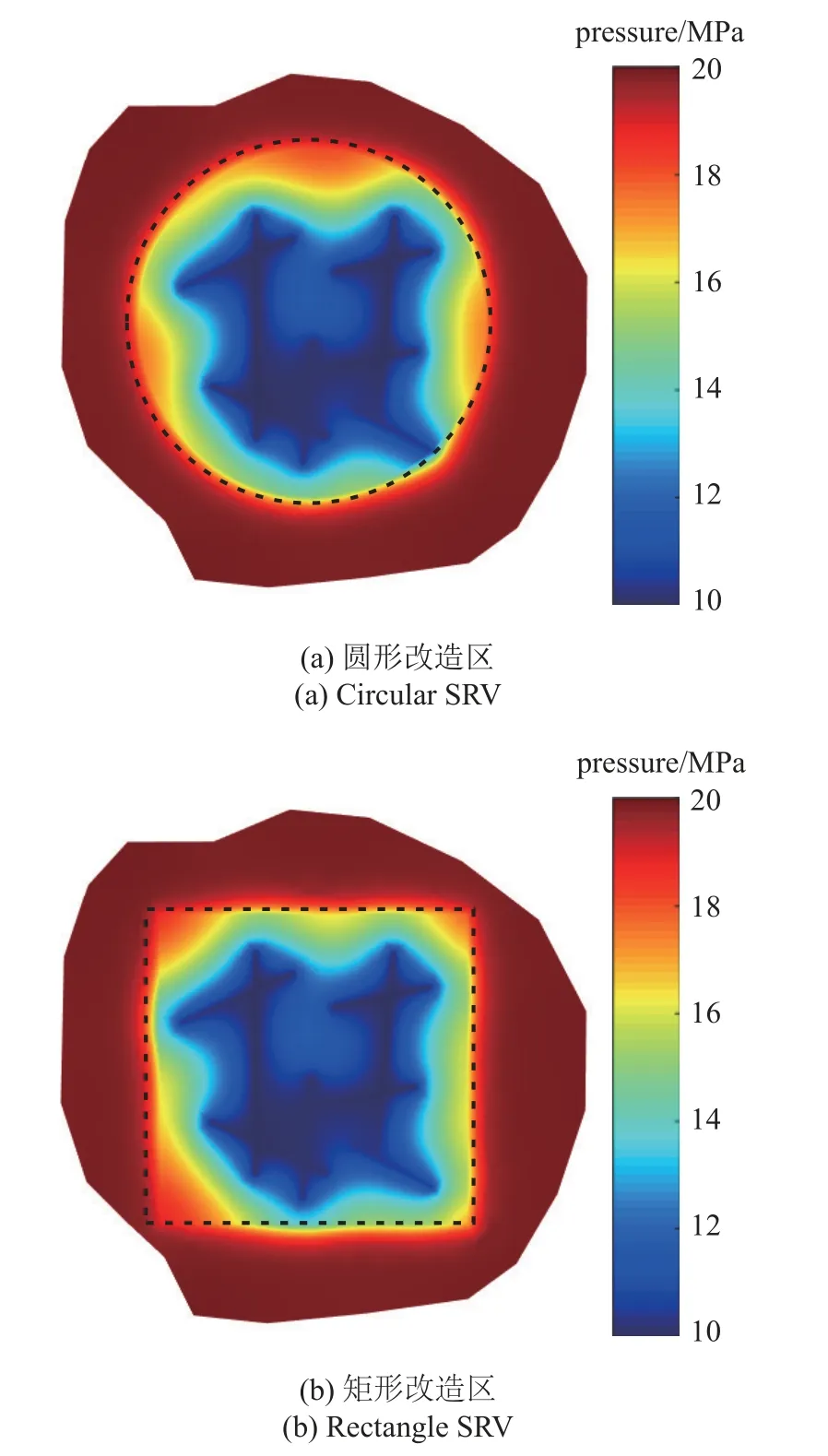
图15 不同SRV 分区模型的压力分布对比(100 d)Fig.15 Comparison of pressure distribution of different SRV zoning models (100 d)

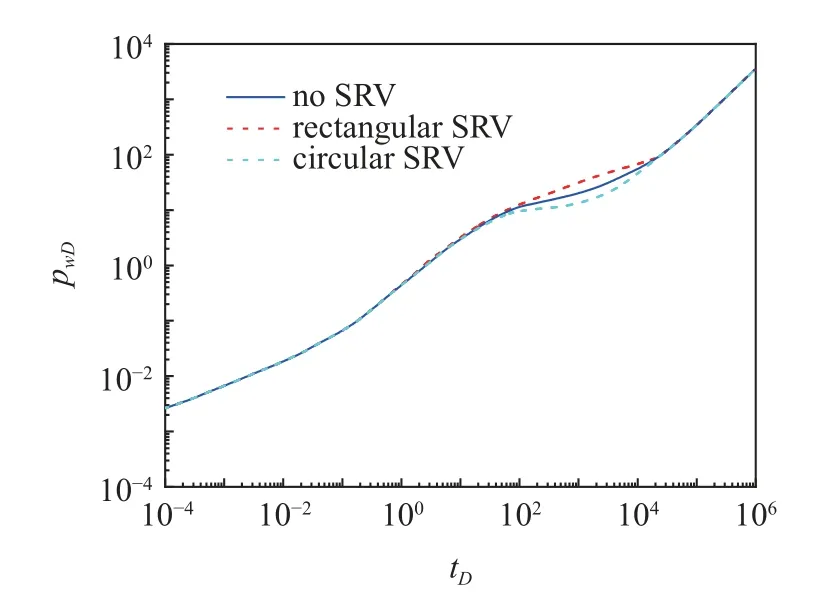
图16 不同SRV 对应的产量动态特征对比Fig.16 Comparison of dynamic production characteristics corresponding to different SRV

5 结论

(1)本文提出了满足局部物质守恒且具有高精度、适用于任意网格剖分的压力流量两套节点的格林元方法,能用于二阶偏微分方程的稳定求解;将两套节点格林元法与EDFM 进行耦合求解,能更精确地获得瞬态压力和流量分布,通过实例验证了本文模型的准确性.

(2)针对原始EDFM 仅适用于矩形网格剖分、难于考虑复杂油藏边界的局限性,本文提出的修正EDFM 能适应任意多边形单元的网格剖分,可适用于复杂油藏边界、缝网及SRV 分区等复杂渗流模型的计算,是对原始EDFM 在网格适用性方面的拓展和升级.