弹性波波场分离方法对比及其在逆时偏移成像中的应用

吴 潇 刘 洋 蔡晓慧

(①中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249； ②中国石油大学(北京)克拉玛依校区石油学院，新疆克拉玛依 834000； ③中国石油大学(北京)CNPC物探重点实验室，北京102249；④南京工业大学岩土工程研究所，江苏南京 210009)

1 引言

进行弹性波逆时偏移成像时，需要将纵、横波解耦分离，以得到物理意义明确的成像剖面[1-4]。通常采用的分离法都是基于纵、横波偏振特性上的差异[5]，统称为基于Helmholtz分解的波场分离法。波场分离法主要有两类：一类是直接分离法，另一类是间接分离法。

直接分离法是直接对矢量波场进行散度、旋度计算，得到纵、横波波场，主要包括空间域分离及波数域分离两种。最早提出的空间域分离法是直接对波场进行散度、旋度运算得到纵波标量波场和横波矢量波场，这类方法得到的波场存在振幅和相位畸变，需做校正[6-8]。在此基础上，Aki等[9]提出空间域矢量分解法，得到的纵波与横波均为矢量，且在同一分量上与原波场分量极性一致，可直接解决成像时极性反转问题。但空间域的矢量波场分离法也会在一定程度上改变波场的振幅、相位及物理意义。Zhu[10]研究了改进的空间域矢量分离法，通过求解一个与原波场满足泊松方程的矢量场，再对该矢量场做波场分解，实现了保幅的波场分离效果。此外， Zhang等[11]发展了在波数域进行分离的方法[12，13]，将空间域波场变换到波数域，通过对波数做归一化处理，可保证分离后波场的振幅、相位及物理意义。

间接分离法是对矢量波场进行散度、旋度计算，并利用以前时刻分离纵、横波波场递推得到下一个时刻的分离纵、横波波场[14-18]。该方法由马德堂等[14]提出，直接在波场延拓的过程中得到分离的纵波和横波波场。在此基础上，Xiao等[19]通过在原始波场中减去纵波波场，得到分离后的横波波场，减少了横波波场递推的计算量。这一类方法得到的纵、横波波场与原始波场一致[19，20]。上述两类方法在弹性波逆时偏移和全波形反演中都得到广泛应用，促进了多波多分量地震勘探的发展。

本文首先回顾了现有的五种基于Helmholtz分解的波场分离法的基本理论，然后分别利用均匀介质模型、层状介质模型以及Marmousi模型对其波场分离效果进行对比，并将分离后的纵、横波场用于弹性波逆时偏移中。通过分析不同波场分离法的优缺点及其波场分离效果对弹性波逆时偏移成像结果的影响，可以为不同情况下采用合适的波场分离法提供有益的参考。

2 弹性波波场分离方法对比

2.1 波场分离方法

在均匀介质中，弹性波波动方程可表示为[9]

(1)

式中：U(x,y,z)为位移矢量；λ和μ为拉梅系数；f(x,y,z)为震源项。由于纵、横波在x方向和z方向上都有投影，正演模拟和实际野外地震勘探采集数据都是纵、横波耦合在一起的。在做逆时偏移等成像处理时，首先需要将纵波波场和横波波场分离开来，从而得到清晰且物理意义明确的成像结果。广泛使用的是Helmholtz分解[5]。由纵、横波的偏振特性可知，纵波波场的旋度为零，横波波场的散度为零，则有

(2)

式中：UP表示纵波分量；US表示横波分量。

因此，原始波场可完全分解为纵波波场(无旋场)与横波波场(无散场)两部分，即

U=UP+US

(3)

2.1.1 直接分离方法

(1)直接分离得到纵、 横波标量波场的空间域方法

常规的Helmholtz分解方法是在空间域直接对波场进行散度运算和旋度运算[5]，求散度得到纵波标量波场，求旋度得到横波矢量波场，即

(4)

(2)直接分离得到纵、 横波矢量波场的空间域方法

Aki等[9]提出了在空间域分离得到纵、横波矢量波场的方法，分离公式为

(5)

(3)改进的直接分离得到纵、横波矢量波场的空间域方法

Zhu[10]改进Aki等[9]的方法提高分离精度。改进的方法引入一个新的矢量场W，使其与原速度场U满足矢量泊松方程

(6)

(7)

利用式(2)与式(3)，可得

(8)

通过求解泊松方程得到W，即可分别计算纵波波场和横波波场。

(4)直接分离得到纵、 横波矢量波场的波数域方法

Zhang等[13]将Aki等[9]的方法发展到波数域，以提高分离精度，其计算公式为

(9)

2.1.2 间接分离方法

马德堂等[14]从波动方程出发，结合纵、横波偏振特性，推导出纵、横波分离的弹性波动方程为

(10)

在波场延拓过程中，可通过有限差分方法递推计算矢量纵、横波场。

Xiao等[19]和Wang等[20]提出可通过从全波场中减去纵波波场得到横波波场，即

US=U-UP

(11)

为了叙述方便，以下将直接分离得到纵、横波标量波场的空间域方法简称为常规方法，直接分离得到纵、横波矢量波场的空间域方法简称为空间域直接分离法，改进的直接分离得到纵、横波矢量波场的空间域方法简称为改进的空间域直接分离法，直接分离得到纵、横波矢量波场的波数域方法简称为波数域直接分离法。

图1展示了以上五种基于Helmholtz分解的波场分离法的发展历程及相互关系。常规方法改变了纵、横波场的振幅和相位及原有的物理意义，且存在极性问题。空间域直接分离法校正了波场极性，但也存在振幅和相位差异。改进的空间域直接分离法不仅能保证振幅和相位的准确性，同时还具有严格的物理意义，但求解泊松方程需要较大的计算量。波数域直接分离法通过对波数进行归一化处理，保证了分离后的波场与原波场一致，但对每个时刻的波场进行傅里叶变换也需要增加较大的计算量。间接分离法在波场延拓的过程中分别递推下一时刻的纵、横波场，提高了分离精度，但分离得到的纵、横波波场在界面处存在能量异常，需要对模型进行平滑处理[11]。

图1 基于Helmholtz分解的波场分离法

2.2 波场分离效果对比

分别采用均匀介质模型、层状介质模型与Marmousi模型进行波场正演模拟，利用以上五种波场分离法对纵、横波场进行分离，并对波场分离结果进行分析和对比。

2.2.1 均匀介质模型

均匀介质模型尺寸为4000m×4000m，纵、横波速度分别为4000、2500m/s，密度为2.25g/cm3。采用交错网格时空域优化有限差分方法[21-23]进行正演模拟，计算边界应用PML吸收边界条件[24]。空间采样间隔为10m，时间采样间隔为1ms。震源采用15Hz的Ricker子波，位于速度模型中心。

图2为正演模拟得到的0.4s时刻的波场快照及常规方法分离得到的纵、横波分离结果。分离得到的纵、横波波场均为标量波场，其中纵波波场在震源左、右两侧存在极性反转，在震源上、下两侧不存在极性反转，而横波波场在震源上、下两侧存在极性反转，在左、右两侧不存在极性反转。利用转换波进行逆时偏移成像时，在成像界面左、右两侧会存在极性反转现象。

图2 均匀介质模型常规方法分离结果

图3 均匀介质模型四种方法分离效果对比 (a)x分量； (b)z分量

从左至右依次为0.4s时刻原始波场、分离得到的横波波场、纵波波场及分离后波场相加与原始波场的残差；为便于比较，将四种分离法所得波场各取1/4置于四个象限中，每个波场快照中左上为空间域直接分离法，右上为改进的空间域直接分离法，左下为波数域直接分离法，右下为间接分离法

图3显示了采用四种不同矢量分离法得到的x分量和z分量纵、横波波场。由图中可见，针对均匀介质，各方法都能得到较好的分离结果，但在波场振幅和相位上还存在一些差异。采用空间域直接分离法得到的纵、横波波场与原始波场差异较大(图3左上部分)。其他三种矢量分离法得到纵、横波波场相加后与原始波场的误差均较小。其中改进的空间域直接分离法存在极少量的能量泄露(图3右上部分)。而波数域直接分离法得到的波场中还存在少量由于傅里叶变换引入的噪声[8]。间接分离法在均匀介质中分离效果最好，得到的纵、横波场与原始波场一致。如图4所示， 单道数据对比更清晰地显示

图4 抽取的x=2500m处四种矢量分离法得到的z分量横波波场快照中单道数据对比

第1道为原始波场，第2～第5道依次为空间域直接分离法、改进的空间域直接分离法、波数域直接分离法、间接分离法得到的横波，第6～第9道依次为四种方法分离得到的纵波，第10～第13道依次为四种方法分离的残差了分离效果的差异。

2.2.2 层状介质模型

层状介质模型(图5)尺寸为4000m×4000m，上下层纵、横波速度分别为vP1=4000m/s，vS1=2500m/s，及vP2=5000m/s，vS2=3200m/s，层厚均为2000m。震源位于(2000m，1500m)处，采用相同的参数进行正演模拟。图6显示了正演模拟t=0.5s时刻波场快照及常规方法得到的纵、横波分离结果，与均匀介质模型试算结果类似，纵、横波分离得干净，但同样存在极性问题。图7～图10分别显示了采用四种不同矢量分离法得到的x分量和z分量纵、横波分离结果。从图中可看出，各方法都能得到较好的分离结果。其中，当存在速度突变时，采用间接分离法得到的纵、横波波场在界面处会存在异常，如图10中箭头所示。 分析其原因是间接分离法在波场延拓过程中，未考虑在界面处纵、横波发生转换的情况，因此在界面处还有能量残留。

图5 层状介质模型示意图

图6 层状介质模型常规方法分离结果

图7 层状介质模型空间域直接分离法得到的结果

图8 层状介质模型改进的空间域直接分离法得到的结果

图9 层状介质模型波数域直接分离法得到的结果

2.2.3 Marmousi模型

采用相同的正演模拟参数，针对Marmousi模型(图11)进行正演模拟及波场分离测试，Marmousi模型尺寸为5000m×3250m(对应于501×353个网格点)，震源位于(2500m，10m)处。

图12显示了正演模拟t=1.0s时刻的波场快照及通过常规方法得到的纵、横波分离结果。图13～图16分别显示了采用四种不同矢量分离法得到的x分量和z分量纵、横波分离结果。从图中可看出，针对Marmousi模型，一次反射和透射的纵、横波能量都能得到有效分离。其中，波数域直接分离法得到的波场存在极少量傅里叶变换产生的人工噪声； 间接分离法得到的纵、横波波场在速度突变处存在能量异常；通过改进的空间域直接分离法的分离效果最好，但相加后的波场与原始波场相比存在少量的能量泄露。与前文理论分析结果一致。

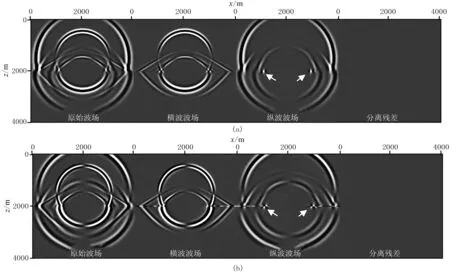
图10 层状介质模型间接分离法得到的结果

为了对比各种波场分离法的计算效率，在正演模拟过程中采用不同分离法对每一时刻的波场进行

波场分离，统计了不同方法正演模拟的总耗时，如表1所示。可以看出改进的空间域波场分离法耗时最长，波数域方法和间接分离法耗时适中，两种空间域分离法耗时最小，与理论分析一致。

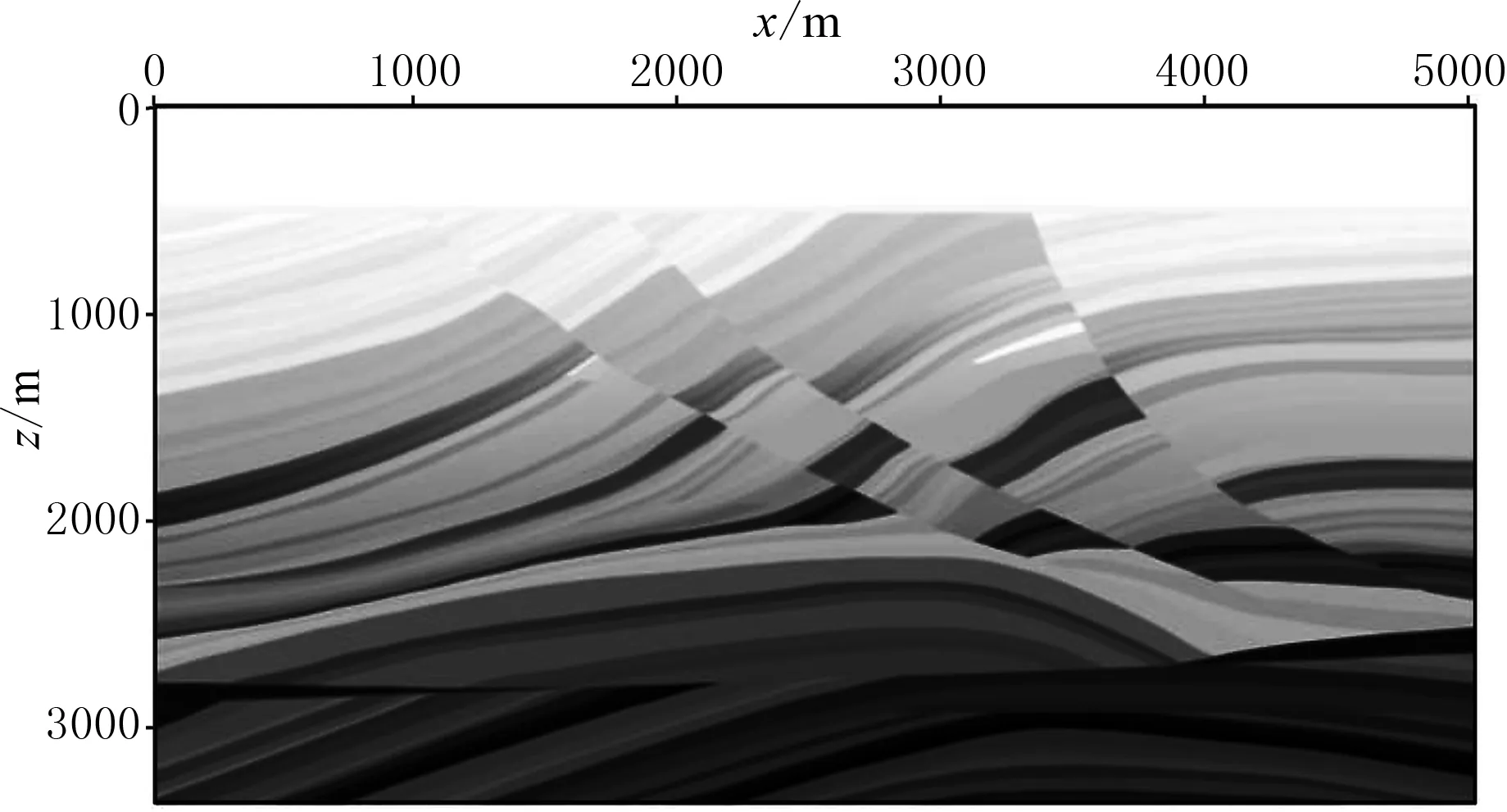
图11 Marmousi模型示意图

图12 Marmousi模型常规方法分离结果

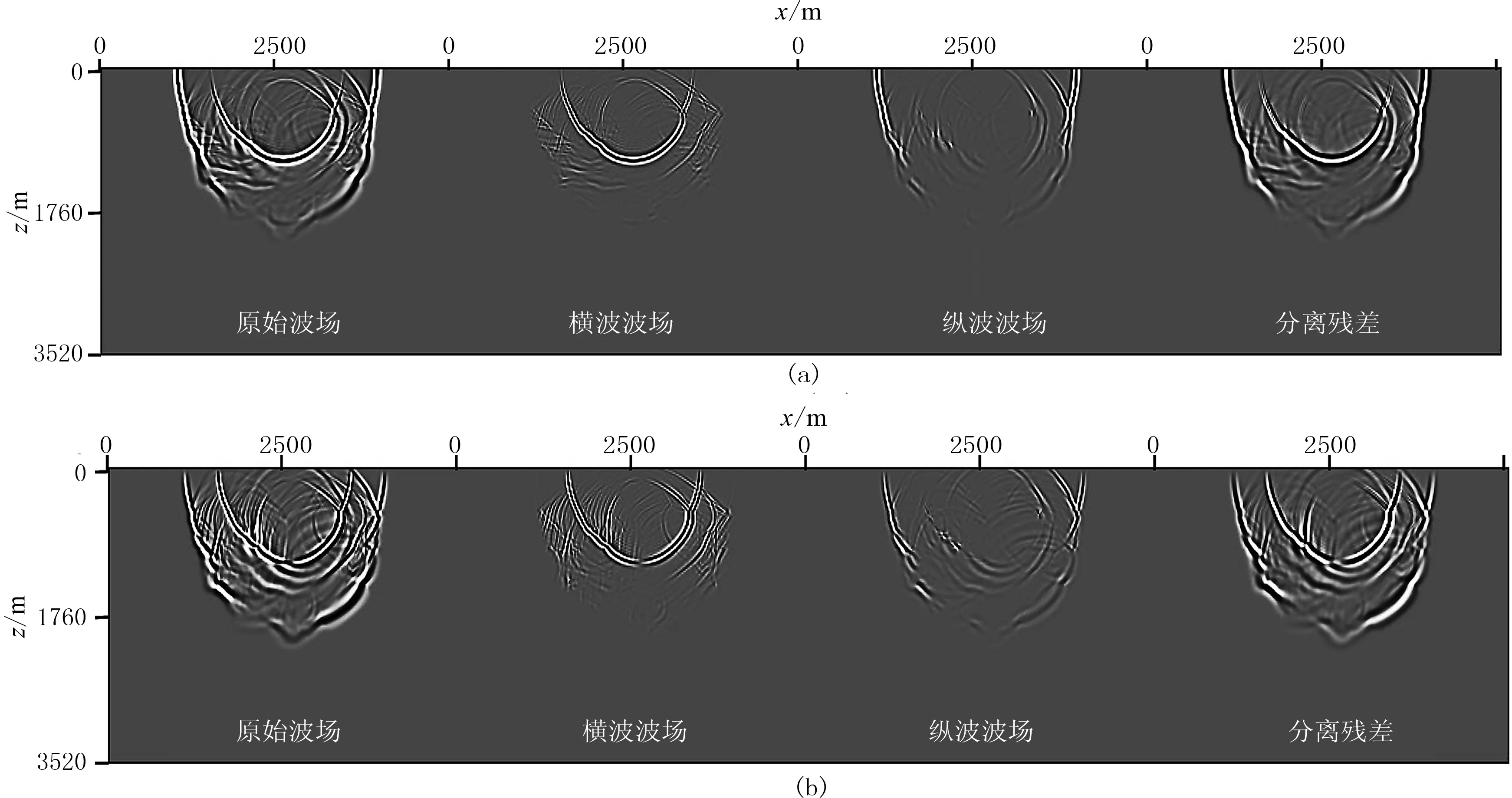
图13 Marmousi模型空间域直接分离法得到的结果

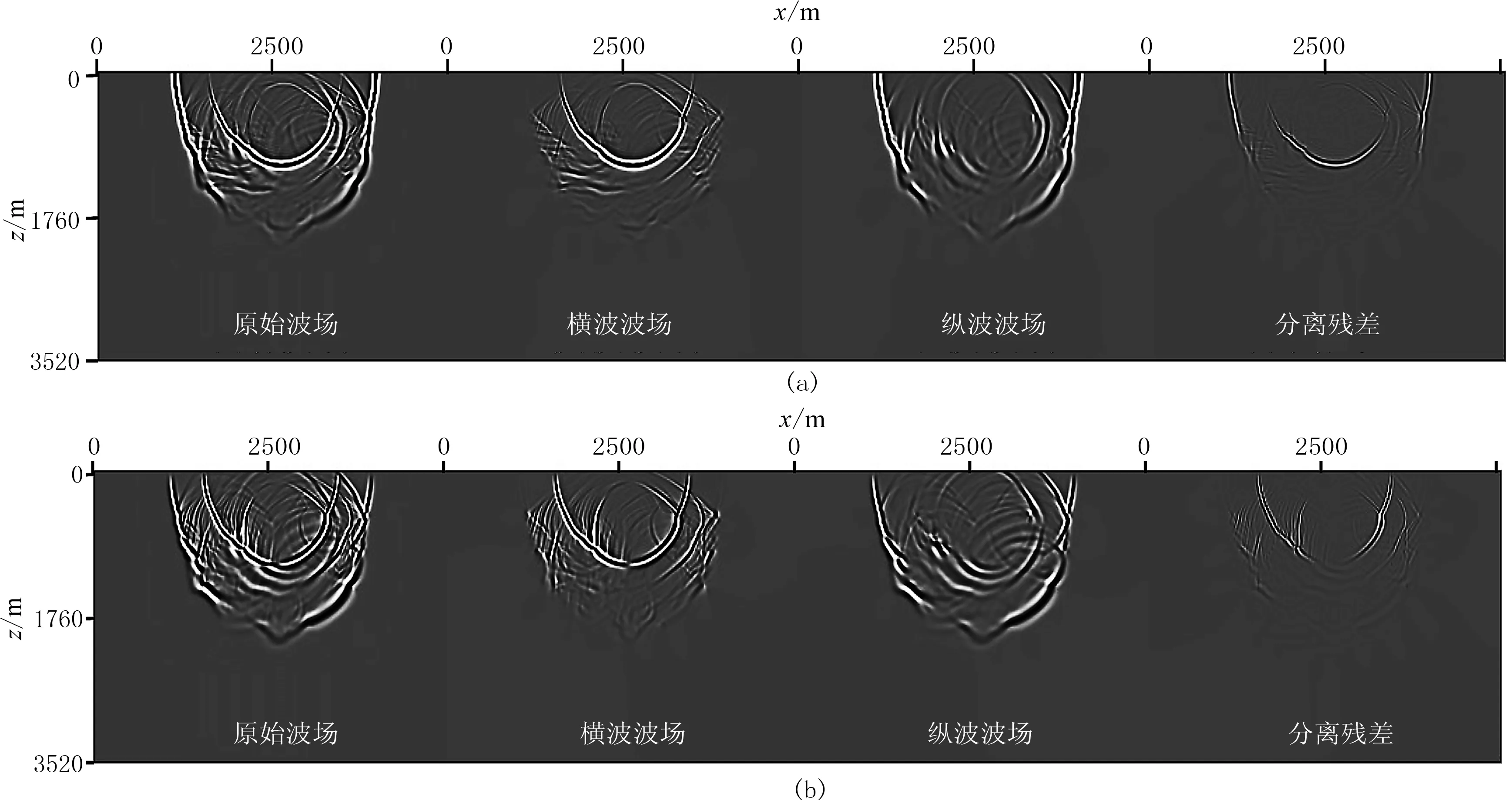
图14 Marmousi模型改进的空间域直接分离法得到的结果

模 型模型网格尺寸正演模拟时长/s未进行波场分离/s常规方法s空间域直接分离法/s改进的空间域直接分离法/s波数域直接分离法/s间接分离法/s均匀模型401×4010.447.7752.9358.99101.1667.6871.79层状模型401×4010.559.6665.5273.05124.0283.3888.25Marmousi模型501×3531.0134.37147.05164.31274.71232.11199.83

图15 Marmousi模型波数域直接分离法得到的结果

图16 Marmousi模型间接分离法得到的结果

3 弹性波逆时偏移成像

3.1 矢量波场的标量成像条件

采用基于矢量波场的归一化标量成像条件[25-27]，以下行纵波震源为例

(12)

式中：·表示两个矢量的内积；S(x,t)和R(x,t)分别表示t时刻的震源波场及检波点波场，其中x表示成像点空间坐标；IPP和IPS分别表示震源纵波波场与检波点纵波波场、震源纵波波场与检波点转换横波波场的偏移成像结果。

3.2 Marmousi模型试算

为了对比以上五种分离法得到的纵、横波波场对于弹性波逆时偏移成像结果的影响，采用Mar-mousi模型进行试算。震源位于地表，共51炮激发，炮间距为10m。正演模拟记录长度为4.0s，时间采样间隔为1ms，震源采用雷克子波，主频为15Hz。对最终的成像结果进行Laplace滤波以去除成像低频噪声。其中，对于常规方法的转换波成像剖面，在单炮偏移剖面的震源右侧乘以-1以近似解决极性反转的问题[28]。

如图17所示为采用五种不同分离法得到的纵、

图17 五种不同波场分离法得到纵、转换波场的逆时偏移成像剖面

横波波场应用于逆时偏移的成像结果。左侧为震源纵波波场与检波点纵波波场成像结果，右侧为检波点横波波场与震源纵波波场成像结果。可见波场分离结果对最终的成像剖面的振幅及界面信息存在一定影响，且转换波偏移成像结果对波场分离效果更敏感。通过常规方法和空间域直接分离法两种方法得到的波场由于振幅和相位有畸变，导致最终的成像剖面上深层能量较弱，界面成像模糊。改进的空间域直接分离法和波数域直接分离法得到的波场由于很好地保存了原始波场的特征，最终的成像剖面上深层能量较强，界面刻画清晰。间接分离法得到的波场同样也能得到较好的成像结果，但是由于分离得到的波场在界面处存在异常，导致最终成像剖面上界面处也存在一些能量异常。

此外，通过对单炮逆时偏移计算时间(表2)进行对比发现，常规方法所需的分离计算量最小，逆时偏移所需的计算时间也最少，但成像效果较差；空间域直接分离法和间接分离法的计算量相对适中，成像结果也较常规方法的成像结果更清晰；而波数域直接分离法和改进的空间域分离法由于需要对每个时刻的波场进行傅里叶变换，导致所需时间最长，但是成像结果也最好。

表2 采用不同波场分离法进行逆时偏移单炮计算耗时对比

4 结论

通过对比五种基于Helmholtz分解的纵、横波波场分离效果及相应的逆时偏移成像结果，得到以下结论：

(1)基于Helmholtz分解的五种方法在模型试算中都可以获得较好的纵、横波分离结果，但是各方法的计算效率与分离效果存在差异。与常规方法相比，四种矢量分离法都解决了转换波逆时偏移中存在极性反转的问题。其中： 间接分离法成像效果很好，但在界面处存在能量异常现象； 改进的空间域直接分离法和波数域直接分离法均具有较好的保幅性，保存了原始波场的特征，深层构造成像效果更好。

(2)为了使弹性波逆时偏移达到实用化，需要综合考虑不同波场分离法的实际应用情况，选择合适的纵、横波分离法，平衡计算效率与分离精度。