基于线性分解的解析信号法估算品质因子Q

刘 洋 李向阳 杨东方

(①西京学院，陕西西安 710123； ②中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249； ③中国石油大学(北京)CNPC物探重点实验室，北京 102249； ④英国地质调查局，Edinburgh，UK； ⑤火箭军工程大学，陕西西安 710025)

1 引言

地震波在地下介质中传播，能量发生衰减，主要因素有非固有衰减和固有衰减两类。其中，非固有衰减包括几何扩散、反射透射损失及层间颗粒散射等，固有衰减主要指与地层介质非均匀黏弹特性有关的吸收衰减，属于介质内在属性的本征衰减。由于介质对高频成分的吸收比低频严重，导致地震波谱向低频移动，子波波形改变，降低了地震资料的分辨率。因此，研究地下介质对地震波的吸收特性，对于改善地震资料分辨率、油气地球物理属性反演和储层描述等有着重要的意义[1]。

品质因子Q是表征介质吸收衰减特性的常用参量之一，与岩石物性、孔隙度、流体类型和流体饱和度等因素有关[2]，Q值越小，吸收越严重。常规的Q值提取方法包括三类：时间域、频率域和时频域[3]。时间域方法主要有振幅衰减法、上升时间法[4]和解析信号法[5]等。频率域方法有谱比法(LSR)[6，7]、质心频移法(CFS)[8-10]、峰值频率法[11，12]和属性组合法[13，14]等。时频域方法是在时频谱上利用频率域方法提取Q值[15-17]，或是对初始地震子波谱作一定假设(如脉冲谱)并推导新的Q值估算式，如小波域能量衰减法、小波域峰值尺度法等[18-20]。地震数据一般是时间域信号，时间域估算Q值是最直接且便于操作的方法，但时间域方法的实际应用受到较大的限制。例如，利用振幅衰减法可提取视衰减，但无法区分固有衰减和非固有衰减；上升时间法的理论精度较低，上升时间的提取存在一定的困难，且抗噪性较低。解析信号法是理论精度较高的方法，其原理是衰减前后子波的瞬时振幅比值的对数与平均瞬时频率之间存在线性关系，实际应用可分两种方法：一是最大值法，即利用最大瞬时振幅处的信息反演Q值，其鲁棒性较低；二是线性近似法，取多个采样点的瞬时信息进行线性拟合(类似于谱比法)，但易受采样率和瞬时频率提取精度的限制，且子波持续时间内的瞬时频率分布范围较窄，不利于斜率拟合[21]。鉴于时间域方法的理论精度低且实际应用困难，人们更倾向于采用频率域或时频域方法估算Q值。但受噪声及复合波的影响，提取较为准确的地震子波谱难度较大，随之降低了Q值的估算精度。另有一些学者将频率域方法转换到时间域实现，如以时间域记录包络峰值处的瞬时频率来估算质心频率[22-25]，为Q值估算提供了很好的思路。

本文基于Futterman衰减理论，对地震子波谱指数衰减项进行一阶近似展开，反变换到时间域，推导了解析信号衰减关系式，将衰减后记录的解析信号表征为衰减前记录解析信号及其导数的线性组合。基于该关系式，建立品质因子Q与线性组合系数的映射关系，形成基于时间域解析信号线性分解的品质因子估算方法。

2 基本原理

假设衰减前地震子波为s(t)，频谱为S(f)，在均匀介质中传播时间Δt后衰减为r(t)，频谱为R(f)，介质的品质因子为Q。根据Futterman衰减理论，有

R(f)=cS(f)e-mf

(1)

(2)

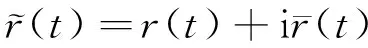
(3)

当mf取值足够小时(如小于0.1)，将指数衰减项展开为一阶线性近似形式，有

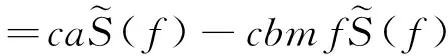
(4)

式中：a、b分别为指数项e-mf展开后的常数项和一次项系数，当不存在先验Q值信息时，可取Taylor级数展开系数，即a=b=1。

式(4)两边分别做反Fourier变换，并结合Fourier变换求导定理，可得

(5)

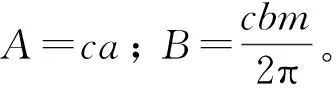
(6)

本文基于最小平方准则提取线性系数A和B(具体推导见附录A)，取式(5)的实部(也可以取虚部或复信号，不影响结果)参与计算，有

(7)

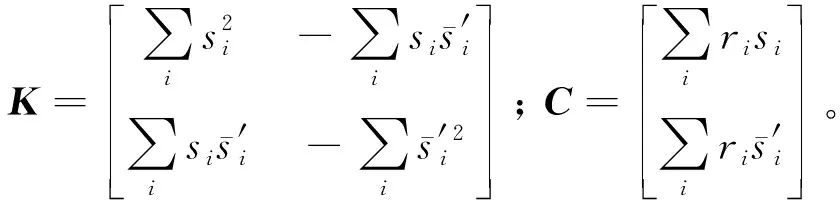
3 模型测试

3.1 单层介质

选取主频为50Hz的Ricker子波作为衰减前地震子波，传播介质为均匀介质，Q值为100，传播时间为30ms，按Futterman衰减理论正演生成衰减子波。图1是衰减前、后地震子波，两个子波间除了地层的吸收衰减外，还有非固有衰减项c(本例取值为0.5，具体数值不影响结论)。

将图1所示的衰减前、后地震子波转化为解析信号，代入式(7)计算的线性系数A=0.5005，B=-7.6214×10-5。图2是衰减后地震子波按照式(5)进行线性分解的示例。式(6)中的一阶展开项b/a取值为1.0，根据线性系数A、B反演的地层Q值为98.5，相对误差为1.50%。作为对比，提取衰减前后记录最大瞬时振幅处的信息，采用常规解析信号法估算Q值，如非固有衰减项得到完全补偿，结果为99.92，精度较高；如非固有衰减项未获补偿，结果为50.30，误差较大，表明常规解析信号法更易受数据品质的影响。

图1 地震子波衰减正演模拟曲线

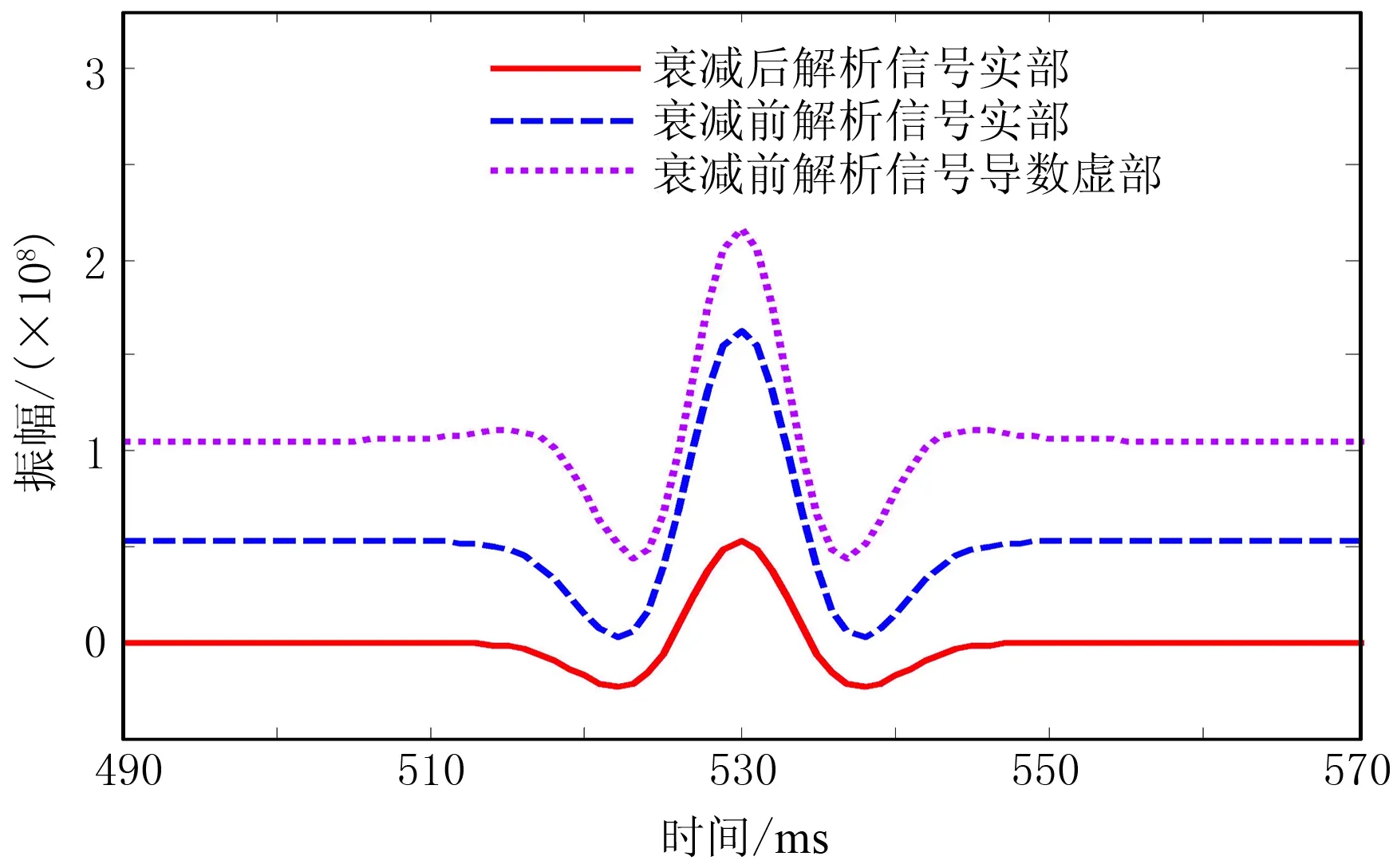
图2 衰减前、后地震子波解析信号对比

3.2 系数a和b的影响

在式(6)的推导过程中，误差主要来源于式(4)指数衰减项的一次展开，当mf取值较小(如mf<0.1)时，展开系数取a=b=1(即Taylor一阶展开)可满足理论精度；但随着mf取值的增加，展开误差将加大，需要对该项的误差进行仿真测试，供实际应用参考。下面考察Q值估算精度受不同传播时差Δt的影响(其他参数不变，mf取值随Δt的增大而增大)。

衰减前地震子波选取主频为50Hz的Ricker子波，Q值为100，传播时差Δt从1ms逐渐增加为400ms，分别利用式(6)反演介质Q值(取b/a=1.0)。图3红线是反演的Q值曲线，可见当传播时差小于100ms时，反演结果的相对误差在10%以内，当传播时差大于100ms时，反演误差不断增加，在400ms处反演Q值达160，误差较大，这主要由一次近似展开引起。当Δt>100ms时，频率f取主频50Hz，mf>0.15不再是一个小量，指数项的一阶近似展开将产生较大的误差，影响Q值的估算。因此，准确估计一次展开系数a、b是提高Q值估算精度的关键。

在没有先验Q值信息的情况下，展开系数取a=b=1。如果有先验的Q值信息，根据mf的取值范围(频率f一般为0～100Hz)，可以对指数衰减项e-mf进行高精度的一次拟合，得到更准确的展开系数a、b。在图3中，尽管传播时差在100～400ms时反演的Q值精度较低，但可以作为指数项高精度一次拟合的先验信息，用于展开系数的估计。图4为拟合得到的展开系数比b/a， 可见随时差Δt的增大，比值逐渐减小(偏离Taylor一阶展开式对应的比值1.0)。将展开系数比代入式(6)，可反演系数修正后的Q值(图5)。图6为b/a修正前、后的Q值反演结果的相对误差曲线，可以看出，当时差Δt较大时，系数修正后反演精度明显高于修正前，相对误差控制在10%以内； 当时差Δt较小时(本例中Δt<70ms)，系数修正前、后的Q值相对误差都在10%以内，修正后Q值的反演精度反而稍低于修正前，这是因为此时的误差主要来源于式(7)中矩阵求逆过程，用展开系数修正不能起到预期的效果。因此，得到一个定性的结论：在Q值较大、传播时差较小(如mf小于0.1)的情况下，展开系数比b/a可直接取1.0；在Q值较小、传播时差较大(如mf大于0.1)的情况下，展开系数比b/a需要进行高精度的拟合。

图3 Q值反演结果随Δt的变化曲线

图4 一次展开系数比b/a

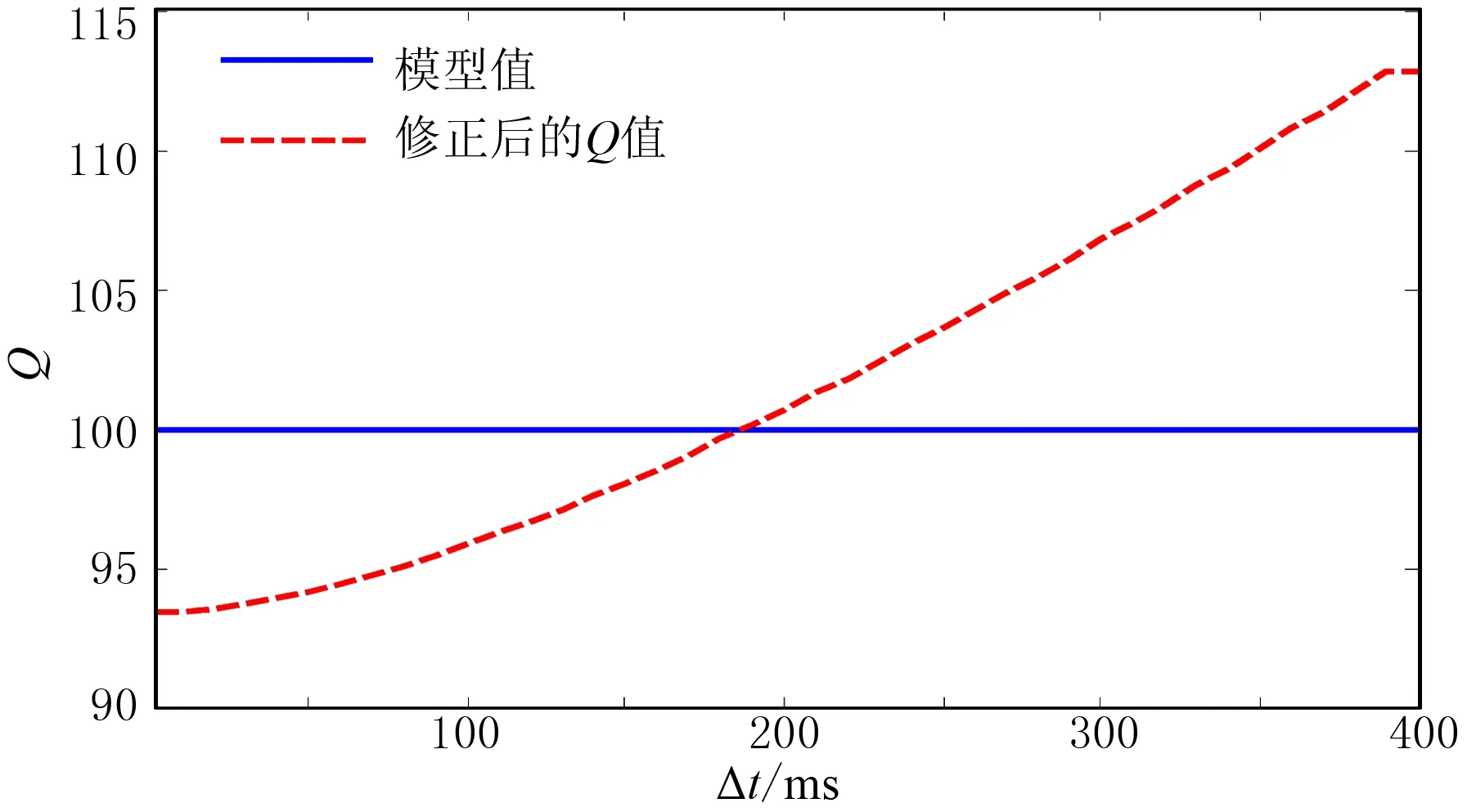
图5 展开系数修正后的Q值反演结果

图6 展开系数修正前、后的Q值反演结果相对误差对比

3.3 层状介质

首先，设计一个层状介质模型(共6层)，总深度为1000m，各层厚度、速度及Q值参数如表1和图7所示，道间距为10m。根据Futterman衰减模型生成VSP下行波记录，并考虑与反射/透射损失有关的能量衰减(假设各层密度相同，反射系数只与纵波波速有关)，初始子波取主频为50Hz的Ricker子波，模拟的零井源距VSP下行波记录如图8所示。

表1 模型参数表

应用式(6)提取Q值(相邻道之间进行反演)，反演结果如图9所示。由图可见，新方法反演的Q值(红线)能较好地反映地层Q值 (蓝线)，与模型值的变化趋势基本保持一致。图10是反演结果的相对误差曲线，在5%以内。

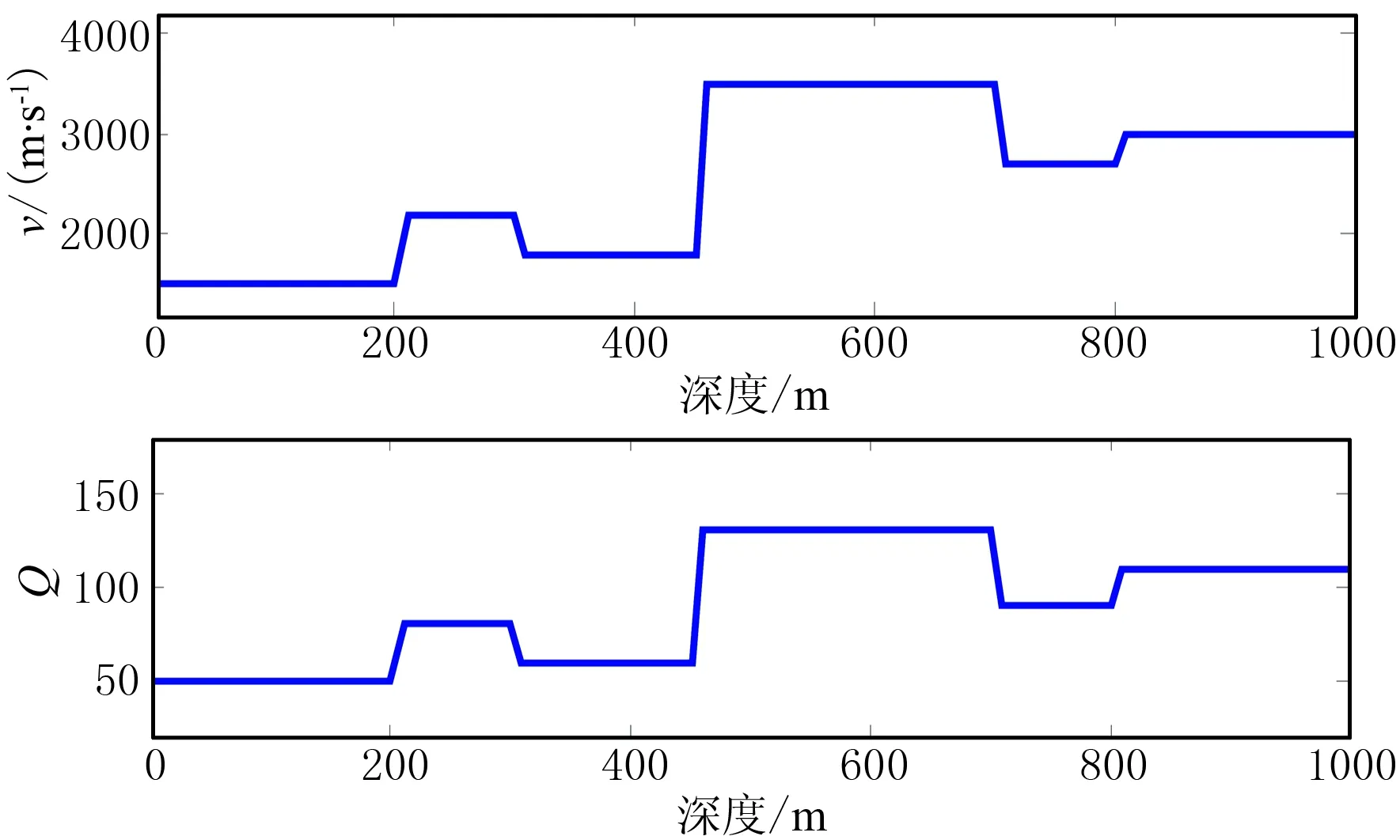
图7 层状模型速度(上)和Q值(下)曲线

图8 零井源距VSP直达波记录

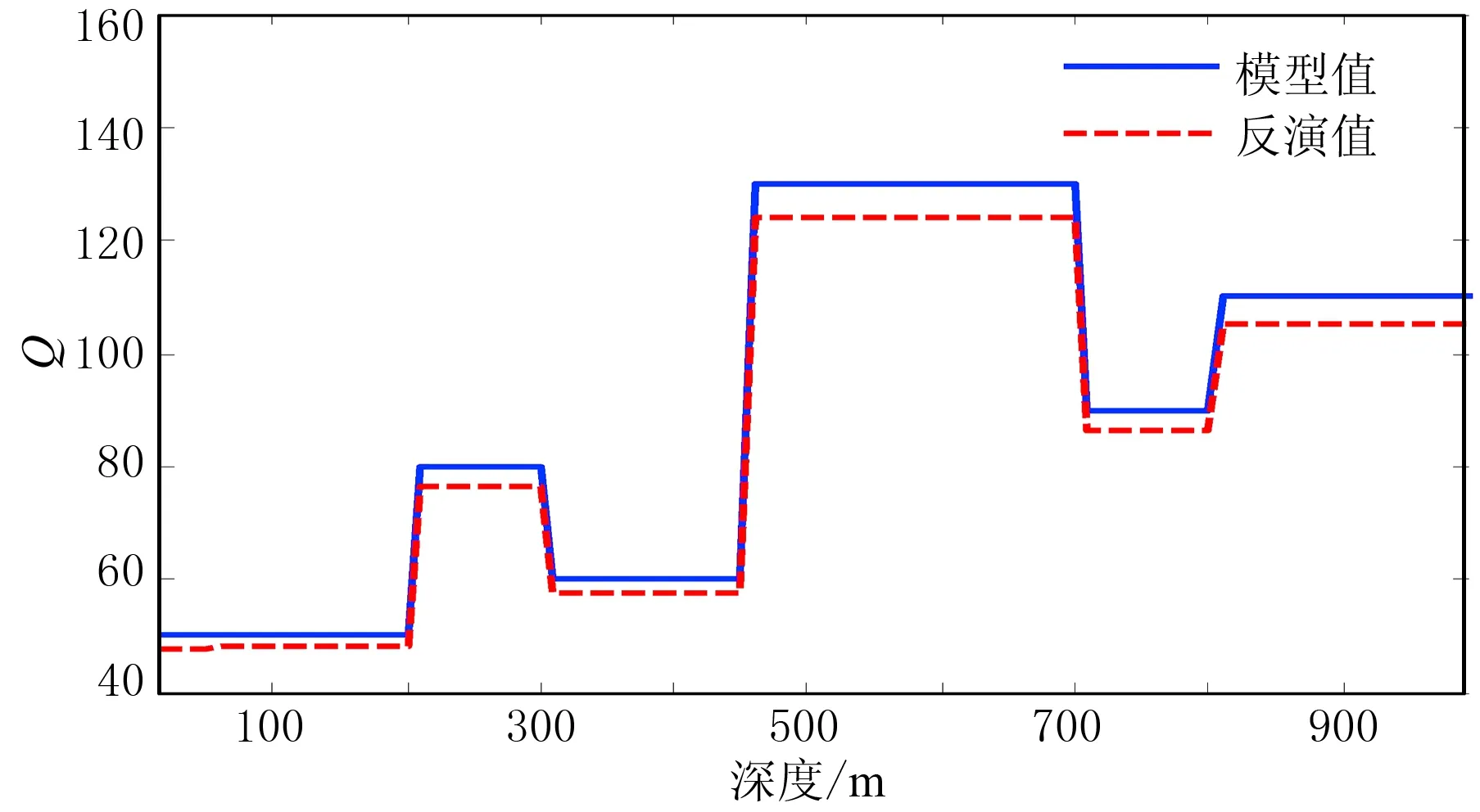
图9 层状模型Q值反演结果

图10 层状模型Q值反演结果的相对误差曲线

4 实际资料应用

图11a为陆上某区块的零井源距VSP原始记录，检波器在500～3130m井段等间隔分布。受上行波场的影响，直达波场的吸收衰减信息提取难度较大，需要进行波场分离提取下行波场，提高各道下行波记录(图11b)的信噪比。图12是提取的各道初至波，随深度的增加，初至波的能量逐渐衰减，延迟时间逐渐增大，分辨率逐渐降低。

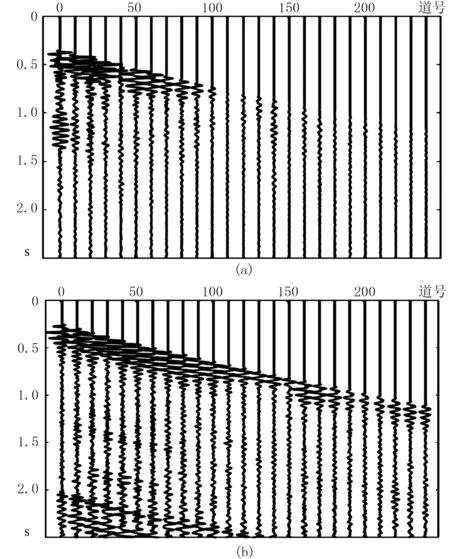
图11 实际零井源距VSP记录

由于该地区地层速度较高，相邻道之间的衰减量过小，利用相邻道记录估算Q值稳定性较差，因此采取间隔10道的方式求取Q值。 图13a是相邻10道的时差曲线，可以看出150～200道之间存在高速体；图13b为根据式(6)和式(7)得到的线性组合系数比曲线。由时差曲线和组合系数比曲线，利用式(6)可反演地层Q值(图14)。本文所求得的Q值为相邻10道之间的等效Q，较由速度曲线求得的经验Q值略小，但趋势基本一致，且对深层高速体的Q值估算具有较好的稳定性。由此可以看出，本文方法提取的Q值具有较高的可信度。

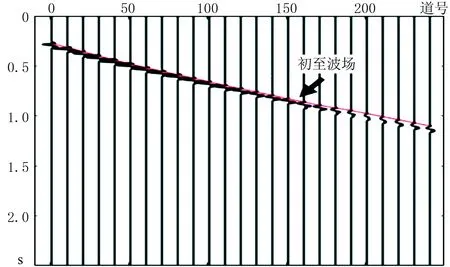
图12 提取的初至波红色实线为初至波到达时刻

图13 时差曲线(a)和线性组合系数比(b)曲线

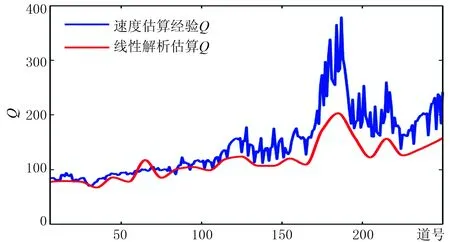
图14 Q值反演结果

5 结论

基于线性分解的解析信号法是一种在时间域直接提取Q值的方法，为Q值的估算提供了一种新的思路和手段，参与计算的记录长度不限，可根据实际情况合理选取。与常规解析信号法相比，新方法不需要计算瞬时频率，不依赖资料的预处理(非固有衰减补偿)品质。模型测试和实际资料处理结果表明，新方法能较好地反演Q值，具有一定的可信度。

附录A 基于最小二乘法的线性拟合推导

将式(5)的实部和虚部分开，则有

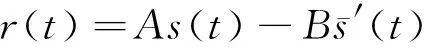
(A-1)

(A-2)

理论上，式(A-1)与式(A-2)是等价的，下面的推导基于式(A-1)。

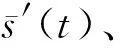
(A-3)

(A-4)