交错网格与旋转交错网格对VTI介质波场分离的影响分析

韩 冬 杜启振, 张明强 郭成锋 公绪飞

1) 中国山东青岛266580中国石油大学(华东)地球科学与技术学院2) 中国天津300451中海油田服务股份有限公司



交错网格与旋转交错网格对VTI介质波场分离的影响分析

1) 中国山东青岛266580中国石油大学(华东)地球科学与技术学院2) 中国天津300451中海油田服务股份有限公司

利用交错网格有限差分和旋转交错网格有限差分进行各向异性介质弹性波场数值模拟时， 质点振动速度分量与应力张量的网格节点定义方式均不相同， 从而对各向异性波场分离效果产生不同的影响． 针对这一问题， 本文以具有垂直对称轴的横向各向同性(VTI)介质的波场分离为例， 首先分析了两种网格的参数定义方式以及VTI介质波场的分离过程； 其次， 详细研究和分析了这两种网格的参数定义方式对各向异性介质波场分离的影响， 并依据波前面连续性以及波场分离效果等方面， 通过数值模拟实验对该影响进行分析验证. 结果表明， 旋转交错网格的参数定义方式更有利于进行各向异性介质波场数值模拟和波场分离．

波场分离 交错网格 旋转交错网格 有限差分 VTI介质

引言

随着勘探技术的发展， 多分量地震技术逐渐受到业界的重视(孙歧峰， 杜启振， 2011)． 为了充分利用多分量资料的纵横波信息， 处理流程通常都包括波场分离环节(董敏煜， 2002)． 依据不同的处理方法， 可将波场分离技术分为两大类(李庆忠， 王建花， 2000). 第一类是基于标量波场理论的波场分离技术， 即对地震记录实现纵波与横波的波场分离． 工业界通常将多分量地震记录的垂直分量视为P波， 并利用坐标旋转得到径向(R)和切向(T)分量， 然后采用相对成熟的声波处理流程对上述分量分别进行处理． 除此之外， 还可利用极化滤波(Etgen， 1988； 李志远等， 2013)、f-k滤波(Amundsenetal， 1998)、τ-P变换(许世勇等， 1999)、 拉东(Randon)变换(冯晅等， 2011)、 平面波分解(Devaney， Oristaglio， 1986)等方法实现对地震记录纵横波的波场分离． 第二类是基于矢量波场理论的分离技术， 即在波场传播过程中实现对波场快照的波场分离． 在各向同性介质方面， Sun和McMechan(2001)基于亥姆霍兹(Helmholtz)分解理论提出利用散度和旋度算子实现P波与S波的波场分离， 但会引入90°相移． 针对这一问题， Sun等(2001)利用希尔伯特(Hilbert)变换实现了相位校正． 相对于各向同性介质， 各向异性介质波场分离的难点在于质点振动方向与波场传播方向并不完全平行或正交， 因此不能直接利用散度和旋度算子进行波场分离(Yan， Sava， 2009a， b)． Dellinger和Etgen(1990)依据克里斯托弗尔(Christoffel)方程， 在波数域中将弹性波场向偏振方向投影， 从而得到qP波和qS波． 在此基础上， Yan和Sava(2009a， b)进一步计算得到空间域不同尺寸空间窗的波场分离算子， 并利用该算子与波场值卷积得到qP波和qS波． 此外， Zhang和McMechan(2010)还提出了一种在波数域获得每个笛卡尔坐标分量上保幅qP波和qS波的波场分解方法． 与第一类波场分离技术相比， 第二类波场分离技术更能够描述波场在地下介质中传播的矢量特性． 因此， 针对第二类波场分离技术展开研究具有重要意义．

弹性波场数值模拟是实现第二类波场分离的前提． 有限差分法由于其计算效率高、 占用内存小以及便于实现等优点而成为弹性波场数值模拟的重要工具． 相对于中心规则网格有限差分法， 交错网格有限差分法(Madariaga， 1976)的精度更高且频散压制效果更好， 因此被广泛应用于各种介质的波场数值模拟中. 例如： Virieux(1984， 1986)利用交错网格有限差分法模拟了各向同性介质中SH波、 P波及SV波的传播； Carcione和Helle(1999)利用交错网格有限差分法实现了孔隙介质中弹性波场的数值模拟； 裴正林(2004)利用交错网格高阶有限差分法实现了三维各向异性介质弹性波数值模拟． 但交错网格有限差分法的不足之处在于质点振动的速度分量定义在不同的网格点上， 利用这种差分格式进行数值模拟得到的波场值不能够直接应用到Yan和Sava(2009a， b)所提出的各向异性介质波场分离方法中． 而旋转交错网格(Saengeretal， 2000)将所有的应力分量定义在同一网格点上， 将所有的质点振动速度分量定义在另一网格点上， 且由旋转交错网格有限差分得到的波场值能够直接应用到各向异性介质波场分离过程中． 同时， 采用旋转交错网格有限差分进行数值模拟时， 弹性模量无需进行插值处理(严红勇， 刘洋， 2012)． 综上可见， 旋转交错网格有限差分更适于各向异性介质波场数值模拟及其波场分离过程．

本文拟以具有垂直对称轴的横向各向同性(transversely isotropic with a vertical axis， 简写为VTI)介质的波场分离为例， 从波场分离的实现过程出发， 对比分析交错网格和旋转交错网格的参数定义方式对VTI介质波场分离(Yan， Sava， 2009a)造成的影响， 并通过数值试验对其进行分析验证， 以进一步说明旋转交错网格在各向异性波场数值模拟及其波场分离方面的优势.

1 VTI介质一阶速度-应力方程及两种网格定义方式

二维情况下， VTI介质一阶速度-应力方程(Virieux， 1986)为

(1)

式中：vx和vz分别为x方向和z方向的质点速度分量；τxx和τzz为正应力，τxz为切应力；C11,C13,C33和C55为刚度系数；ρ为密度． 分别采用交错网格有限差分(Madariaga， 1976)和旋转交错网格有限差分(Saengeretal， 2000)对式(1)进行数值模拟．

图1给出了交错网格(Virieux， 1986)和旋转交错网格(Saengeretal， 2000)应力场和速度场的定义方式示意图， 其中： 实线表示定义在时间上的主网格， 虚线表示在时间t上交错了Δt/2的半网格；O点为参考点，P1点和P2点分别代表某一点x方向和z方向上的质点振动速度分量． 比较图1a与图1b可知， 质点振动的速度分量在交错网格中没有定义在同一个网格节点上， 而在旋转交错网格中则定义在同一个网格节点上．

图1 交错网格(a)和旋转交错网格(b)示意图

2 VTI介质波场分离过程

VTI介质中， qP波与qS波的偏振方向相互垂直， 利用偏振矢量将波场投影至偏振方向可得到qP波和qS波(Dellinger， Etgen， 1990)． 在波数域中， 通过求解克里斯托弗尔方程， 可得qP波和qS波的偏振矢量. 二维情况下求解

(2)

可得qP波的偏振矢量UqP为

(3)

qSV波的偏振矢量UqSV为

(4)

图2 空间域波场分离算子. (a) x方向; (b) z方向

3 两种交错网格对波场分离的影响

这里以qP波的波场分离过程为例， 详细阐述两种交错网格对VTI介质波场分离所产生的影响．

波数域和空间域中的qP波(Yan，Sava， 2009a)分别表示为

(5)

(6)

波数域和空间域中各速度分量的傅里叶变换对为

(7)

(8)

如图1a所示， 在交错网格中， O点处的质点振动速度分量可利用P1和P2点处的质点振动速度分量表示为

(9)

如图1b所示， 在旋转交错网格中， O点处的质点振动速度分量可利用P1和P2点处的质点振动速度分量表示为

(10)

将式(9)和式(10)带入式(6)， 可得

(11)

(12)

此即为空间域中的qP波.

Yan和Sava(2009a)提出的VTI介质波场分离方法是将Vx(kx, kz)和Vz(kx, kz)以及vx(x, z)和vz(x, z)视为同一个网格节点上的质点振动速度分量进而实现波场分离． 对比式(11)与式(12)可得， 由于交错网格质点振动速度分量未定义在同一个网格节点上， 导致用于VTI介质波场分离的x方向质点振动速度分量比z方向多出平移算子exp(-i2πkxΔx/2), z方向质点振动速度分量比x方向多出平移算子exp(-i2πkzΔz/2)， 从而造成波场分离不彻底. 针对这一问题，Zhang和McMechan(2010)利用两点平滑估算其中间值， 从而得到同一个网格节点上的质点振动速度分量， 但该方法只是对波场中间值的近似， 并不能完全表示两点中间的波场值．Du等(2014)提出在波数域中对波场值进行平移校正， 从而实现两点中间值的准确求取； 但鉴于本文采用的VTI介质波场分离方法(Yan，Sava， 2009a)的处理流程是在空间域中进行的， 这种波数域中的插值方法将会造成额外的计算量， 故不适用于本文．

如式(12)所述， 由旋转交错网格有限差分得到的用于波场分离的x方向与z方向的质点振动速度分量在网格节点上的对应位置保持一致， 不需要进行额外的插值处理， 同时可避免因波场插值造成的波场值不准确及效率降低等问题． 另外， 在使用旋转交错网格进行波场数值模拟的过程中也不需要对弹性模量进行插值处理.

4 数值算例

本节将采用均匀VTI介质模型进行弹性波场数值模拟和波场分离， 通过模拟测试结果对比分析交错网格和旋转交错网格对VTI介质波场分离(Yan，Sava， 2009a)造成的影响. 本文采用的模型网格大小为600×300， 水平方向和垂直方向的空间采样间隔均为10m， 时间采样间隔为0.001s， 模型参数如表1所示． 交错网格有限差分和旋转交错网格有限差分均采用空间8阶、 时间2阶进行弹性波场数值模拟， 利用非分裂完全匹配层(non-splittingperfectmatchedlayer， 简写为NPML)对边界反射进行吸收衰减． 震源子波选取主频为35Hz的雷克子波， 其解析式为f(t)=[1-2(πfpt)2]exp[-(πfpt)2]， 式中fp为子波主频； 震源位置坐标为(2800m, 500m)．

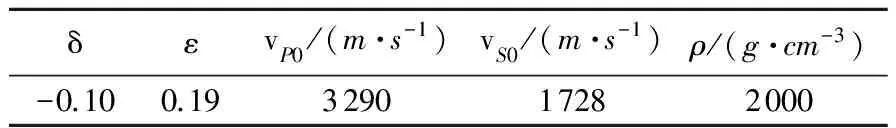
表1 均匀VTI介质参数表

在弹性波场数值模拟过程中， 提取第400个时间步长(即第400ms)的质点振动速度x分量与z分量的波场快照进行波场分离， 以阐明这两种交错网格对VTI介质波场分离所造成的影响．

图3和图6分别为交错网格和旋转交错网格波场数值模拟得到的波场快照. 对比图3与图6可知， 采用两种交错网格有限差分进行波场数值模拟均能得到清晰的波场快照． 图4给出了直接利用交错网格波场数值模拟得到的波场快照进行波场分离得到的qP波和qS波； 图5给出了利用交错网格波场数值模拟并进行两点平均插值处理后的波场快照进行波场分离得到的qP波和qS波(Zhang，McMechan， 2010)． 可以看出， 经过两点插值处理后进行波场分离得到的结果要优于未采用波场插值处理直接进行波场分离的结果； 但如图4和图5中箭头所指位置所示，qP波中仍然残留有qS波，qS波中同样残留有qP波， 且qS波中的残留现象更为严重． 图7为旋转交错网格波场数值模拟得到的波场快照进行波场分离的结果． 比较图4、 图5及图7中箭头和方框所示可知， 使用旋转交错网格数值模拟得到的波场值进行波场分离得到的qP波和qS波较为干净彻底， 且qP波的连续性较好．

图3 交错网格数值模拟得到的波场快照(400 ms). (a) x分量； (b) z分量

图4 交错网格数值模拟得到的波场快照直接进行波场分离的结果. (a) qP波; (b) qS波

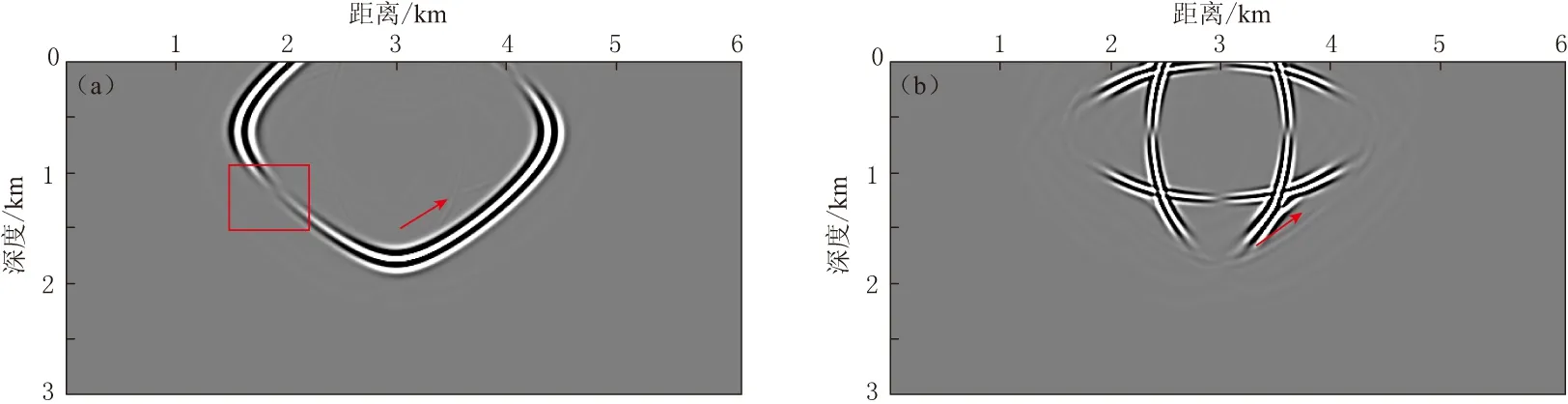
图5 交错网格数值模拟得到波场快照并进行两点平均插值处理后进行波场分离得到的结果. (a) qP波; (b) qS波

图6 旋转交错网格数值模拟得到的波场快照(400 ms). (a) x分量； (b) z分量

图7 旋转交错网格数值模拟得到的波场快照直接进行波场分离得到的结果. (a) qP波; (b) qS波

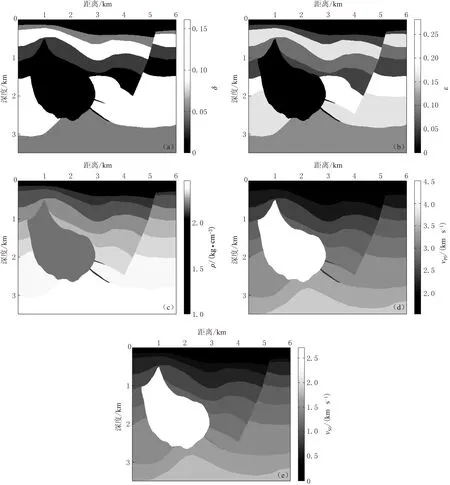
图8 VTI 介质Hess模型. (a) δ; (b) ε; (c) ρ; (d) vP0; (e) vS0

图9 Hess模型交错网格波场数值模拟结果及波场分离结果(a) x分量波场快照； (b) z分量波场快照； (c) qP波； (d) qS波

图10Hess模型旋转交错网格波场数值模拟结果及波场分离结果(a) x分量波场快照； (b) z分量波场快照； (c)qP波； (d)qS波

Fig.10SnapshotsforHessmodelbyusingrotatedstaggered-gridnumericalsimulationandtheseparationresults. (a) x-componentsnapshot； (b) z-componentsnapshot； (c)qP-wave； (d)qS-wave

为了进一步说明使用旋转交错网格波场数值模拟得到的波场值进行波场分离的优势， 本文采用如图8所示的VTI介质Hess模型进行波场数值模拟和波场分离． 模型网格大小为600×350， 水平方向和垂直方向的采样间隔为10m， 时间采样间隔为0.001s； 采用主频为35Hz的雷克子波， 震源位置坐标为(3200m, 700m)； 交错网格有限差分和旋转交错网格有限差分均采用空间8阶、 时间2阶进行弹性波场数值模拟； 采用非分裂完全匹配层对边界反射进行吸收衰减， 同时选取600ms的波场快照进行波场分离． 图9和图10分别给出了利用交错网格和旋转交错网格进行数值模拟得到的波场快照以及对波场快照进行波场分离的结果， 对比其中红色箭头标示处可验证， 使用旋转交错网格波场数值模拟得到的波场值进行波场分离得到的qP波与qS波分离效果良好．

5 讨论与结论

本文针对交错网格和旋转交错网格对VTI介质波场分离造成的影响进行了详细分析， 并选取简单模型和复杂模型进行了相应的数值实验， 得到如下结论：

1) 直接采用交错网格有限差分所得波场快照进行波场分离， 无法彻底分离qP波与qS波； 尽管通过对模拟结果进行简单的算术平均插值处理后再进行波场分离， 能够在一定程度上提高波场分离的效果， 但仍不能彻底解决波场无法完全分离的问题．

2) 采用旋转交错网格有限差分所得波场快照进行波场分离， 能够得到分离较为彻底的qP波和qS波， 且无需进行任何插值处理．

因此， 当对各向异性介质进行波场数值模拟并进行相应的波场分离时， 旋转交错网格有限差分是一种较为理想的选择．

评审专家和编辑部对本文提出了宝贵意见和建议， 中国石油大学(华东)EWEP课题组提供了帮助， 作者在此表示衷心的感谢.

董敏煜. 2002. 多波多分量地震勘探[M]. 北京: 石油工业出版社: 76--83.

DongMY. 2002. Multi-Wave and Multi-Component Seismic Exploration[M].Beijing:PetroleumIndustryPress: 76--83 (inChinese).

冯晅， 张先武， 刘财， 王典， 杨庆节. 2011. 带有多道相关的抛物线Radon变换法分离P-P、P-SV波[J]. 地球物理学报， 54(2): 304--309.

FengX，ZhangXW，LiuC，WangD，YangQJ. 2011.SeparatingP-PandP-SVwavebyparabolicRadontransformwithmultiplecoherence[J]. Chinese Journal of Geophysics， 54(2): 304--309 (inChinese).

李庆忠， 王建花. 2000. 多波地震勘探的难点与展望[M]. 青岛: 中国海洋大学出版社: 35--36.

LiQZ，WangJH. 2000. Problems of Multi-Component Seismic Exploration and Its Solutions[M].Qingdao:OceanUniversityofChinaPress: 35--36 (inChinese).

李志远， 梁光河， 谷丙洛. 2013. 基于散度和旋度纵横波分离方法的改进[J]. 地球物理学报， 56(6): 2012--2022.

LiZY，LiangGH，GuBL. 2013.ImprovedmethodofseparatingP-andS-wavesusingdivergenceandcurl[J]. Chinese Journal of Geophysics， 56(6): 2012--2022 (inChinese).

裴正林. 2004. 三维各向异性介质中弹性波方程交错网格高阶有限差分法数值模拟[J]. 石油大学学报： 自然科学版， 28(5): 23--29.

PeiZL. 2004.Three-dimensionalnumericalsimulationofelasticwavepropagationin3-Danisotropicmediawithstaggered-gridhigh-orderdifferencemethod[J]. Journal of China University of Petroleum： Edition of Natural Sciences， 28(5): 23--29 (inChinese).

孙歧峰， 杜启振. 2011. 多分量地震数据处理技术研究现状[J]. 石油勘探与开发， 38(1): 67--73.

SunQF，DuQZ. 2011.Areviewofthemulti-componentseismicdataprocessing[J]. Petroleum Exploration and Development， 38(1): 67--73 (inChinese).

许世勇， 李彦鹏， 马在田. 1999. τ-q变换法波场分离[J]. 中国海上油气: 地质， 13(5): 334--337.

XuSY，LiYP，MaZT. 1999.SeparationofP-andS-wavefieldsviatheτ-qtransform[J]. China Offshore Oil and Gas: Geology， 13(5): 334--337 (inChinese).

严红勇， 刘洋. 2012. 黏弹TTI介质中旋转交错网格高阶有限差分数值模拟[J]. 地球物理学报， 55(4): 1354--1365.

YanHY，LiuY. 2012.Rotatedstaggeredgridhigh-orderfinite-differencenumericalmodelingforwavepropagationinviscoelasticTTImedia[J]. Chinese Journal of Geophysics， 55(4): 1354--1365 (inChinese).

AmundsenL，IkelleLT，MartinJ. 1998.MultipleattenuationandP/SsplittingofOBCdata:Aheterogeneousseafloor[C]∥Proceedings of the 68th Annual International Meeting， SEG， Expanded Abstracts.NewOrleans:SocietyofExplorationGeophysicists: 722--725.

CarcioneJM，HelleHB. 1999.Numericalsolutionoftheporoviscoelasticwaveequationonastaggeredmesh[J]. J Comput Phys， 154(2): 520--527.

DellingerJ，EtgenJ. 1990.Wave-fieldseparationintwo-dimensionalanisotropicmedia[J]. Geophysics， 55(7): 914--919.

DevaneyAJ，OristaglioML. 1986.Aplane-wavedecompositionforelasticwavefieldsappliedtotheseparationofP-wavesandS-wavesinvectorseismicdata[J]. Geophysics， 51(2): 419--423.

DuQZ，ZhangMQ，ChenXR，GongXF，GuoCF. 2014.True-amplitudewavefieldseparationusingstaggered-gridinterpolationinthewavenumberdomain[J]. Appl Geophys， 11(4): 437--446.

EtgenJT. 1988.PrestackmigrationofP-andSV-waves[C]∥Proceedings of the 58th Annual International Meeting， SEG， Expanded Abstract.Tulsa:SocietyofExplorationGeophysicists: 972--975.

MadariagaR. 1976.Dynamicsofanexpandingcircularfault[J]. Bull Seismol Soc Am， 66(3): 639--666.

SaengerEH，GoldN，ShapiroSA. 2000.Modelingthepropagationofelasticwavesusingamodifiedfinite-differencegrid[J]. Wave Motion， 31(1): 77--92.

SunR，ChowJD，ChenKJ. 2001.PhasecorrectioninseparatingP-andS-wavesinelasticdata[J]. Geophysics， 66(5): 1515--1518.

SunR，McMechanGA. 2001.Scalarreverse-timedepthmigrationofprestackelasticseismicdata[J]. Geophysics， 66(5): 1519--1527.

VirieuxJ. 1984.SH-wavepropagationinheterogeneousmedia:Velocity-stressfinite-differencemethod[J]. Geophysics， 49(11): 1933--1942.

VirieuxJ. 1986.P-SVwavepropagationinheterogeneousmedia:Velocity-stressfinite-differencemethod[J]. Geophy-sics， 51(4): 889--901.

YanJ，SavaP. 2009a.Elasticwave-modeseparationforVTImedia[J]. Geophysics， 74(5):WB19--WB32.

YanJ，SavaP. 2009b.Elasticwave-modeseparationforTTImedia[C]∥Proceedings of the 79th Annual International Meeting， SEG， Expanded Abstracts.Houston:SocietyofExplorationGeophysicists: 1197--1021.

ZhangQS，McMechanGA. 2010. 2Dand3DelasticwavefieldvectordecompositioninthewavenumberdomainforVTImedia[J]. Geophysics， 75(3):D13--D26.

Effects of staggered-grid and rotated staggered-grid on the wavefield separation in VTI media

1)SchoolofGeoscience，ChinaUniversityofPetroleum，ShandongQingdao266580，China2)ChinaOilfieldServicesLimited，Tianjin300451，China

Wavefield separation is an important part of multi-component seismic data processing， and the wavefield numerical simulation method is one of the necessary tools to this process. When staggered-grid finite difference scheme and rotated staggered-grid finite difference scheme are utilized to elastic wavefield simulation in anisotropic media， the definition of the particle velocity components and that of the stress tensor are different among these two grids. Furthermore， these two types of definitions will affect the wavefield separation. So we take the case of transversely isotropic media with a vertical axis (VTI media) as an example to analyze. Firstly， we analyze the parameter definition of these two grids and details about the wavefield separation in VTI media. Then， we focus on the analysis on the separation effects caused by the different parameter definition of these two grids. Considering the aspects of wavefront continuation and the purity of wavefield separation， numerical experiments are utilized to verify the results. Finally we draw the conclusion that the parameter definition of rotated staggered-grid is more beneficial to the anisotropic numerical simulation and the wavefield separation.

wavefield separation； staggered-grid； rotated staggered-grid； finite difference； VTI media

国家自然科学基金(41174100)、 国家科技重大专项(2011ZX05019-008-08)和中国石油天然气集团公司(2014A-3609)联合资助.

2015-07-16收到初稿， 2015-10-10决定采用修改稿.

e-mail: multi-wave@163.com

10.11939/jass.2016.01.011

P315.3+1

A

韩冬， 杜启振， 张明强， 郭成锋， 公绪飞. 2016. 交错网格与旋转交错网格对VTI介质波场分离的影响分析. 地震学报, 38(1): 111--121. doi:10.11939/jass.2016.01.011.

Han D, Du Q Z, Zhang M Q, Guo C F, Gong X F. 2016. Effects of staggered-grid and rotated staggered-grid on the wavefield separation in VTI media.ActaSeismologicaSinica, 38(1): 111--121. doi:10.11939/jass.2016.01.011.