基于小波包和峰度赤池信息量准则的P波震相自动识别方法
田优平 赵爱华
1) 中国长沙410004湖南省地震局 2) 中国北京100081中国地震局地球物理研究所
基于小波包和峰度赤池信息量准则的P波震相自动识别方法

1) 中国长沙410004湖南省地震局 2) 中国北京100081中国地震局地球物理研究所
基于小波包变换和峰度赤池信息量准则(AIC), 提出了一种新的自动识别P波震相的综合方法, 即小波包-峰度AIC方法. 首先对由加权长短时窗平均比(STA/LTA)法粗略确定的P波到时前后3 s的记录进行小波包三尺度的分解与重构, 分别计算每个尺度重构信号的峰度AIC曲线并将其叠加, 叠加曲线的最小值则为P波震相到时; 然后对原始地震记录进行有限冲激响应自适应滤波以提高信噪比和识别精度; 最后将小波包-峰度AIC方法应用到合成理论地震图及实际地震记录的P波初至自动识别中. 结果表明: 初至清晰度对识别精度的影响比信噪比对其影响更大; 与单独使用加权STA/LTA方法和峰度AIC法相比, 小波包-峰度AIC法具有更强的抗噪能力, 识别精度更高; 当初至清晰时, 小波包-峰度AIC法自动识别与人工识别的P波到时平均绝对差值为(0.077±0.075) s.
P波震相 有限冲激响应(FIR)数字滤波 震相自动识别 小波包-峰度AIC方法
引言
地震震相的检测和识别是地震学研究中的重要课题, 是地震定位、 地震预警、 地球内部结构、 层析成像、 震源机制等一系列地震研究的基础. 以往的震相识别主要是人工识别, 由于其在很大程度上依赖经验, 所以费时、 费工且又繁杂. 随着全球宽频带地震仪的发展, 地震记录中所包含的信息越来越丰富, 传统的人工识别已不能满足海量地震记录的分析, 因此, 震相自动识别方法应运而生. 该方法能节省大量时间, 大大提高地震速报和预警的效率, 为震后应急救援赢得宝贵时间.
近年来, 基于震相的不同特征发展起来的震相自动识别方法可归纳为单特征法、 多特征法和综合分析方法等3类.
单特征法是根据震相的能量、 频谱、 偏振和分形维等单一特征的变化进行震相的判别和拾取, 其中最常用的是长短时窗平均比(short term average/long term average, 简写为STA/LTA)方法(Stevenson, 1976; Allen, 1978, 1982; Baer, Kradolfer, 1987; 刘晗, 张建中, 2014). 该方法快速简单, 但当信噪比较低或初动不明显时, 效果较差甚至出现误判, 且拾取远震信号到时的精度较低. 近年来震相识别方法以频谱分析方法(如短时傅里叶变换、 小波及小波包变换、 S变换和Cohen类时频分布)中的小波和小波包变换(Yomogida, 1994; 刘希强等, 1998, 2002; 王喜珍, 2004; 杨配新等, 2004)为主. 小波变换克服了短时傅里叶变换的单分辨率分析的不足, 具有可调的时频窗, 在低频区频率分辨率较高, 高频区时间分辨率较高; 小波包变换则对小波变换进行了改进, 具有将随尺度增长而变宽的频谱窗进一步分割变细的优良特性, 其应用前景较好. 此外, 对赤池信息量准则(Akaike Information Criterion, 简写为AIC)的研究也较多, 依据AIC寻求曲线极小点作为背景噪声与有效信号的最佳划分点即震相的到时点. 基于AIC发展起来的一系列震相识别方法, 如基于预测模型的自回归AIC(autoregressive-AIC, 简写为AR-AIC)方法(Sleeman, van Eck, 1999; 王海军等, 2003; Küperkochetal, 2012)、 无需计算自回归阶数的方差AIC(variance-AIC, 简写为VAR-AIC)方法(Maeda, 1985; 曲保安等, 2014)、 直接根据地震图记录计算AIC函数的三阶统计AIC(three-order cumulative-AIC, 简写为TOC-AIC)方法(刘希强等, 2009)、 基于峰度的AIC(Kurtosis-AIC, 简写为Kur-AIC)方法(Küperkochetal, 2010, 赵大鹏等, 2012)以及基于小波变换的AIC(wavelet-AIC, 简写为W-AIC)方法(Zhangetal, 2003). 除上述方法外, 单特征法还有分形分维(Boschettietal, 1996; 常旭, 刘伊克, 2002; 王海军等, 2004)、 高阶统计量(Saragiotisetal, 2002; Küperkochetal, 2010)、 偏振分析(Cichowiczetal, 1988; Jurkevics, 1988)等方法.
多特征法主要是基于地震波传播的整体特征或多个特征来识别震相, 如全波震相分析法(孙进忠等, 1985; 赵鸿儒等, 1990)、 相关法(王继等, 2006; Satrianoetal, 2008)和人工神经网络法等, 其中人工神经网络中的误差反向传播神经网络应用较广(庄东海等, 1994; Dai, MacBeth, 1997; 王娟等, 2004).
综合分析方法一般先利用某种单特征法或其改进算法对震相到时进行粗略估计, 在此基础上结合其它一种或多种单特征法得出各震相比较精确的到时. Bai和Kennett(2000)联合STA/LTA、 自回归分析、 瞬时频率和偏振分析等4种方法来自动识别宽频带地震记录的P波和S波等多种震相并拾取其到时, 大大提高了震相拾取的能力. 毛燕等(2011)通过STA/LTA、 幅值和频率特征初步确定P波到时, 再用最小二乘法和AIC方法精确地确定P波到时.
在进行不同震相的识别时, 每种方法都各有其独特的优势, 但也都或多或少存在一些缺陷. 单特征法在地震记录信噪比高时能取得较好的结果, 但信噪比低或初动不清晰时拾取精度较低; 多特征法中全波震相分析法和人工神经网络法需要较大的工作量, 相关法则主要受续至波和时窗范围的影响较大; 综合分析方法拾取震相的精度相对较高, 但往往计算量较大. 震相自动识别是一项传统而又持续发展的研究课题, 目前还没有完全实现高效的地震震相自动识别. 为此, 本文在前人研究的基础上, 提出了小波包-峰度AIC方法来自动识别P波震相到时, 并将该方法应用到合成理论地震图和云南地区近震P波到时的自动识别中, 以进一步探索提高P波自动识别精度的方法.
1 方法
本文提出小波包-峰度AIC方法来自动识别P波震相到时, 其基本思路为: 首先利用加权STA/LTA方法自动检测出有效的地震事件并粗略地拾取P波初至到时; 然后对粗略拾取的到时前后各推3 s的时间窗内的信号进行小波包三尺度分解重构; 最后分别计算3个尺度重构信号的峰度AIC曲线并进行叠加, 叠加的AIC曲线的最小值即为最终拾取到的精细P波初至到时.
1.1 加权STA/LTA方法粗略拾取P波到时
STA/LTA方法是一种常用的震相识别方法, 具有计算速度快、 简单易行的优点, 其基本原理是用信号短时窗平均值(STA)与长时窗平均值(LTA)之比来反映信号能量或振幅的变化. 当信号到达时, STA比LTA变化快, 相应的STA/LTA值明显增加, 当该比值大于事先设定的阈值时, 则视为地震事件发生, 该点被判定为初至点, 其对应的时间为初至到时.
STA/LTA的计算方法分为标准STA/LTA和递归STA/LTA两种, 其中后者速度快且结果平滑, 因而应用普遍. 递归STA/LTA计算公式为
(1)
(2)
式中, STAi和LTAi分别表示信号在i时刻的短、 长时窗平均值,fc(i)为信号在i时刻的特征函数值,NSTA和NLTA分别表示短、 长时窗包含的记录点数. 特征函数fc选用能同时反映振幅和频率变化的公式
(3)
来计算. 式中,Y(i)为i时刻的地震记录值.
当信噪比低或初动不明显时, STA/LTA算法的结果不太理想. 为此, 武东坡(2004)引入加权系数α对STA/LTA方法进行改进. 设STA/LTA比值为R, 改进后的计算式为
(4)
式中,d为信号的采样间隔,t为时间间隔(t取1—2 s可达理想结果). 当有效信号未到时,α值接近1; 当信号到达时,α值会突然增大, 从而对式(4)中的R值产生显著的放大作用, 有利于更好地识别信噪比低或初动不明显的信号.
本文取短时窗窗长为0.2 s, 长时窗窗长为2 s, 滑动步长为1个采样点, 阈值为8. 运用加权STA/LTA方法可拾取P波初至到时, 并将其作为粗略到时.
1.2 峰度AIC方法
随机变量x的k阶统计量可表示为
(5)
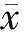
随机变量的峰度(Kurtosis)可衡量分布曲线的尖峭程度, 其表达式为
(6)
用两个时间段数据的峰度作为特征函数fc, 可得峰度AIC的表达式为
(7)
式中,N为特征函数fc的长度.
1.3 一维小波包多尺度分解
Wickerhauser(1992)提出了离散小波包变换公式. 定义算子F0和F1为
(8)
式中, {hm}m∈Z和{gm}m∈Z分别为低通和高通滤波器.
离散小波包变换的表达式可写为
(9)


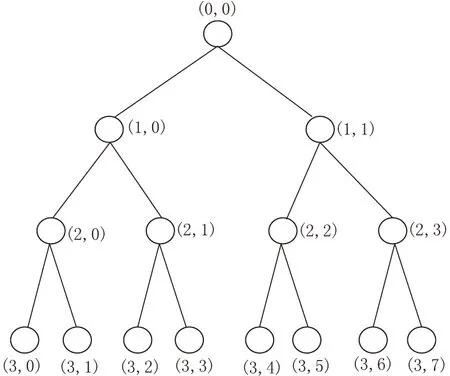
图1 小波包三尺度分解树 Fig.1 Three-scale wavelet packet decomposition tree
由此可见, 小波包具有将随尺度增长而变宽的频谱窗进一步分割变细的优良特性, 它克服了小波变换随尺度增大而导致的频谱局部性变差的缺陷, 能够更精细地对信号进行分析, 更好地描述由于新震相产生而导致地震信号渐变或突变的局部特征.

图2 利用小波包-峰度AIC方法拾取P波到时(a) 垂直向地震波形; (b) 尺度1; (c) 尺度2; (d) 尺度3; (e) 3个尺度叠加
1.4 小波包-峰度AIC方法精确拾取P波到时
图2a给出了云南省元江台记录的2009年7月2日13时2分峨山ML2.8地震垂直向波形. 通过加权 STA/LTA 方法粗略拾取该记录的P波初至到时tP为12.74 s, 与人机交互拾取的到时12.66 s相差0.08 s.
本文首先对地震信号进行小波包三尺度分解, 利用分解的系数对原始信号进行重构; 然后根据式(7)计算3个尺度下[tP-3 s,tP+3 s]时间窗内重构信号的峰度AIC值, AIC曲线最低点即对应P波到时. 图2b--d分别给出了3个尺度下的拾取到时, 分别为12.69 s, 12.67 s和12.67 s. 可以看出, 3个尺度的到时相差很小, 说明地震信号在多个尺度下是相关的(噪声一般随着尺度增加而衰减或不相关). 将3个尺度的峰度AIC曲线叠加得到的曲线最低点作为最终拾取到的精细P波到时. 如图2e所示, 小波包-峰度AIC方法自动拾取的P波到时为12.67 s, 与人机交互拾取的到时12.66 s相差0.01 s. 可见, 在STA/LTA方法的基础上, 本文方法进一步提高了P波识别的精度.
2 理论应用
将本文提出的小波包-峰度AIC方法应用到理论地震记录中, 以检验该方法的有效性. 图3a给出了云南省楚雄台记录的2008年8月31日16时31分地震的垂直向波形, 其合成理论地震图(Wang, 1999; Wang, Wang, 2007)如图3b所示. 运用射线追踪法(赵爱华等, 2003; Zhaoetal, 2004)计算出合成地震记录(图3b)的理论走时为23.37 s. 分别利用加权STA/LTA方法、 峰度AIC方法和小波包-峰度AIC方法(本文方法)自动拾取图3b中P波初至到时, 结果分别为23.54 s, 23.42 s, 23.36 s, 如图4所示, 其与理论到时的绝对差值分别为0.17 s, 0.05 s, 0.01 s.
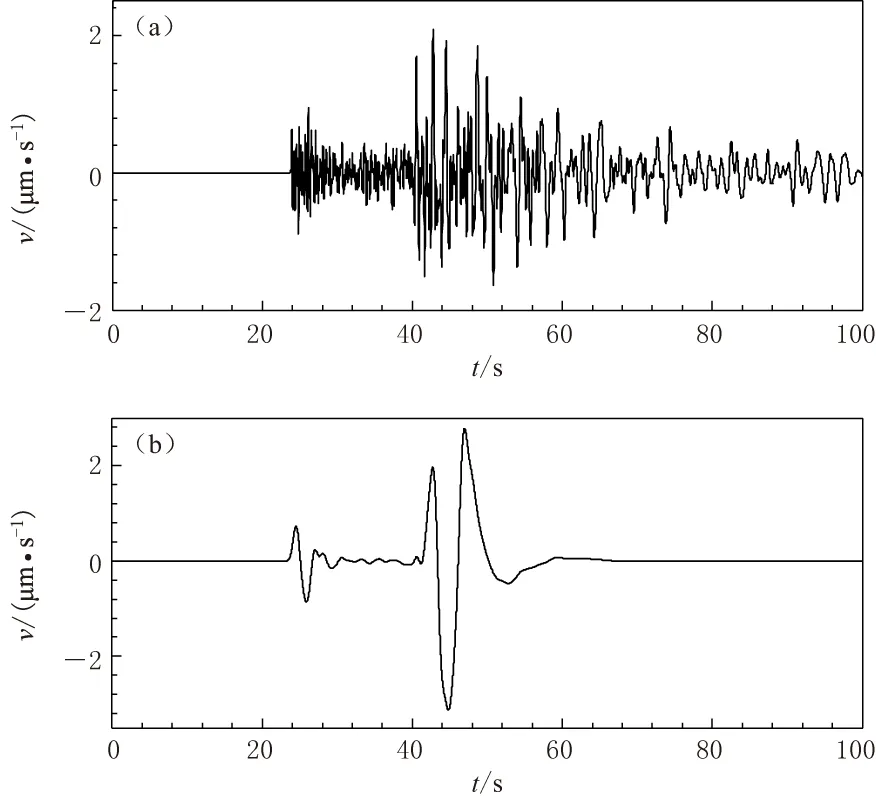
图3 实际地震记录(a)与合成理论地震图(b) Fig.3 Real seismic recording (a) and theoretically synthetic seismogram (b)
向图3b所示的合成理论地震记录中逐渐加入不同信噪比(signal-to-noise ratio, 简写为SNR)的高斯白噪声和实际地震噪声, 以检测各方法的抗噪能力及其拾取P波初至精度的效果. 3种方法拾取P波到时的情况如表1和表2所示. 可以看出, 在合成理论记录中, 无论加入高斯白噪声还是实际地震噪声, 3种方法所拾取的P波到时精度随着信噪比的降低均有一定影响. STA/LTA方法受信噪比影响最大, 随着信噪比降低, 自动拾取与理论计算的P波到时差值ΔT逐渐增大, SNR≥20 dB时ΔT基本在0.3 s以内; 峰度AIC方法随着信噪比减小, ΔT也有一定波动, SNR≥13 dB时ΔT基本在0.3 s以内; 小波包-峰度AIC方法受信噪比影响最小, SNR≥10 dB时ΔT基本在0.3 s以内. 但当信噪比降低到一定值(表1中加入地震噪声SNR<5 dB, 表2中加入高斯白噪声SNR<7.5 dB)时, 由于STA/LTA曲线很难达到事先设定的阈值致使检测不到地震信号, 因而该方法失效.

图4 合成地震记录的P波到时自动拾取(a) 地震垂直向记录; (b) STA/LTA方法; (c) 峰度AIC方法; (d) 小波包-峰度AIC方法

SNR/dB自动拾取的P波初至到时/sSTA/LTA方法峰度AIC方法小波包⁃峰度AIC方法自动与理论到时差ΔT/sSTA/LTA方法峰度AIC方法小波包⁃峰度AIC方法25.0023.5523.4323.380.180.060.0122.0023.5723.4423.390.200.070.0221.0023.5823.4523.390.210.080.0220.0023.5923.4623.390.220.090.0217.0023.6423.5123.420.270.140.0515.0023.6723.5523.470.300.180.1013.6123.7023.5923.510.330.220.1413.0023.7123.6123.540.340.240.1712.0023.7823.6323.560.410.260.1910.0023.9823.6923.600.610.320.239.0024.0423.7123.610.670.340.248.0024.0823.7523.620.710.380.257.0024.1923.7823.640.820.410.276.0024.2023.8123.670.830.440.305.0024.3323.8523.720.960.480.35
总之, 本文提出的小波包-峰度AIC方法在合成理论地震记录中加入不同噪声时表现为抗噪能力更强且拾取的P波到时精度更高; 当加入的实际地震噪声SNR≥8 dB时, ΔT≤0.25 s, 效果要明显优于其它两种方法.

表2 合成理论记录中加入高斯白噪声时3种方法在不同信噪比下拾取P波到时的效果对比
3 实际应用
将小波包-峰度AIC方法应用到实际地震中, 以检验其在实际中的应用效果.
3.1 数据
本文对研究区(97.5°E—107°E, 20°N—30°N)2009年2月—2011年6月107次ML1.4—4.9地震的722个单台垂直向记录进行研究和分析, 涉及的台站共计52个. 选取单台记录的震中距为0.1°—2.29°(约11.12—254.64 km), 大部分分布在0.1°—1.6°(约11.12—177.91 km), 均为近震; 选取事件的震源深度为2.5—11.8 km, 主要分布在5—10 km, 均为浅源地震.
3.2 滤波方法
如上所述, SNR≥8 dB时拾取的P波初至精度较高, 当信噪比太低时拾取的效果不甚满意, 故本文对SNR<8 dB的原始数据进行滤波, 以提高拾取到时的精度.
滤波的主要步骤为: ① 给定一个滤波器组, 频带分别为1.5—3.6, 3.6—8.3, 8.3—10, 10—15, 15—20 Hz; ② 设定信噪比阈值为8 dB, 计算原始信号的信噪比; ③ 若原始信噪比大于阈值, 则认为原始信噪比较高, 无需滤波直接利用原始数据进行处理(Leach Jretal, 1999); ④ 若原始信噪比小于阈值, 则对①中各频带分别进行滤波, 计算滤波后各频带对应的信噪比, 确定信噪比最大时所对应的滤波频带[f1,f2].
鉴于有限冲激响应(finite impulse response, 简写为FIR)数字滤波器的稳定性好, 易实现严格的线性相位, 信号处理后不会产生相位畸变, 应用范围甚广(万永革, 2012), 故本文用FIR数字滤波器(采用等波纹最佳逼近设计线性相位的Remez算法, 是目前最优的FIR设计算法)对[f1,f2]频段内的原始数据(722个地震记录)进行滤波, 本文将该方法称为FIR最佳频带滤波方法.
图5a给出了滤波前后原始记录的信噪比变化. 可以看出: 滤波前信噪比的变化范围为-5.82—37.54 dB, 均值为(9.12±6.76) dB, SNR>8 dB的占50.28%; 滤波后信噪比的变化范围为0.9—38.04 dB, 均值为(14.15±5.03) dB, SNR>8 dB的高达96.12%. 图5b给出了滤波前后P波震相初至识别差值的变化. 可以看出, 滤波前自动拾取与人工拾取的P波震相初至识别差值ΔT′分布较分散, 有些差值过大, 而滤波后的差值分布较为均匀, 基本都在0值附近波动. 由此可见, 经FIR最佳频带滤波后不仅增强了信噪比, 而且有效提高了P波识别精度.

图5 滤波前、 后信噪比(a)及P波初至识别差值ΔT′(b)的对比
3.3 P波初至识别差值、 信噪比及初至清晰度的关系
利用FIR最佳频带滤波方法对722个原始地震记录进行自适应滤波(SNR≥8 dB时不滤波), 然后用小波包-峰度AIC方法自动拾取P波初至到时, 自动拾取与人工拾取的到时差结果见图6a. 可以看出: P波初至识别差值为-1.4—1.2 s, 平均绝对差值为(0.234±0.271) s, 其中绝对差值在0.3 s以内的占75.07%; 随着信噪比的增大, P波到时拾取的精度在一定程度上得到了提高, 说明P波拾取的精度与信噪比有一定关系, 但这种关系并非是信噪比越高P波初至识别差值越小的线性关系.
为了进一步探求P波初至识别差值的影响因素, 本文将722个地震事件按初动清晰度分为初至清晰(初动突出, 肉眼能明显识别)和初至不清晰(初动不突出, 肉眼难以识别)两种情况: 初至清晰时清晰度设为1, 共322个地震记录; 初至不清晰时设为-1, 共400个地震记录. 图6b给出了信噪比与初至清晰度的关系, 可以看出: 初至清晰时信噪比变化范围为8.1—38.04 dB, 平均信噪比为(15.73±5.24) dB; 初至不清晰时信噪比变化范围为0.9—30.66 dB, 均值为(12.88±4.48) dB. 由此可见, 初至清晰时对应的信噪比往往较高, 而信噪比高时初至却不一定清晰.
图6c给出了P波初至识别差值与初至清晰度的关系. 可以看出: 当初至清晰时, P波初至到时差的变化范围为-0.27—0.46 s, 平均绝对差值为0.077 s, 标准差为0.075 s, 平均绝对差值在0.2 s和0.3 s以内的分别占94.41%和98.45%; 当初至不清晰时, P波到时差变化范围为-1.4—1.2 s, 平均绝对差值为0.36 s, 标准差为0.303 s, 平均绝对差值在0.2 s, 0.3 s和0.5 s以内的分别占38%, 56.25%和74%. 由此可见, 初至清晰度对P波初至识别差值的影响较大, 且初至越清晰, P波到时拾取的精度越高.

图6 P波初至识别差值ΔT′、 信噪比及初至清晰度的关系(a) 初至差与信噪比的关系; (b) 信噪比与初至清晰度的关系; (c) 初至差与初至清晰度的关系
通过上述分析可知, P波到时自动拾取的精度与信噪比有一定关系, 但并非呈线性关系, 相对信噪比对其的影响, 初至清晰度对其的影响更大, 初至清晰时到时拾取的精度明显比初至不清晰时高; 同时, 初至清晰时信噪比也较高, 但信噪比高时初至却并不一定清晰. 因此, 可将原始记录分为初至清晰和初至不清晰两种情况, 以检验本文小波包-峰度AIC方法在不同实际情况下自动拾取P波初至到时的效果.
3.4 3种自动识别方法在实际地震中的应用对比
为检验本文小波包-峰度AIC方法在近震P波震相自动识别中的应用效果及识别精度, 将其与STA/LTA方法、 峰度AIC方法这两种常用的震相自动识别方法进行对比分析.
图7和图8分别给出了初至清晰情况下3种方法自动识别与人机交互识别的P波到时结果及其差值分布. 可以看出: 本文小波包-峰度AIC方法所得震相识别结果与人机交互识别结果的平均绝对差值最小, 为(0.077±0.075) s, 到时差为-0.27—0.46 s, 322个单台记录的处理结果中, 绝对差值在0.1 s, 0.2 s和0.3 s以内的分别占73.6%, 94.41%和 98.45%; 峰度AIC方法所得震相识别结果与人机交互所得到时的差值为-0.86—0.7 s, 平均绝对差值为(0.113±0.135) s, 绝对差值在0.1 s, 0.2 s和0.3 s以内的分别占65.84%, 86.96%和93.17%; STA/LTA方法所得震相识别结果与人机交互拾取到时的差值为-0.27—0.98 s, 平均绝对差值为(0.16±0.184) s, 绝对差值在0.1 s, 0.2 s和0.3 s以内的分别占55.28%, 77.33%和85.09%. 这表明, 在初至清晰的情况下, 3种方法自动识别近震P波震相的效果均较好, 其中本文提出的小波包-峰度AIC方法拾取的P波精度最高, 峰度AIC方法次之, STA/LTA方法精度相对低一些.

图7 初至清晰时P波震相自动识别与人机交互识别结果对比图中数值分别为3种方法得到的平均绝对差值. (a) STA/LTA方法;(b) 峰度AIC方法; (c) 小波包-峰度AIC方法
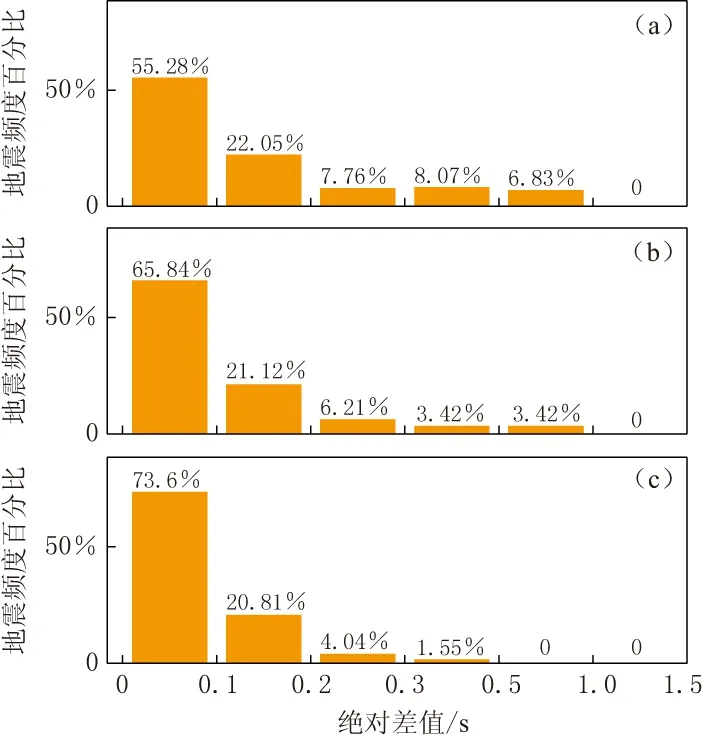
图8 初至清晰时P波震相自动识别与人机交互识别差值分布 (a) STA/LTA方法; (b) 峰度AIC方法; (c) 小波包-峰度AIC方法 Fig.8 Error distribution of the P-wave onset time between automatic recognition and man-machine interaction recognition when first break is clear(a) STA/LTA method; (b) Kurtosis-AIC method; (c) Wavelet packet and Kurtosis-AIC method
图9和图10分别为初至不清晰的情况下3种方法自动识别与人机交互识别的P波到时结果及差值分布. 可以看出: 本文方法所得震相识别结果与人机交互识别结果的平均绝对差值最小, 为(0.36±0.303) s, 到时差值为-1.4—1.2 s, 400个单台记录的处理结果中, 绝对差值在0.2 s, 0.3 s和0.5 s以内的分别占38%, 56.25%和74%; 峰度AIC方法所得震相识别结果与人机交互拾取的到时差值为-1.34—1.37 s, 平均绝对差值为(0.373±0.314) s, 绝对差值在0.2 s, 0.3 s和0.5 s以内的分别占37.75%, 53.75%和71.75%; STA/LTA方法所得震相识别结果与人机交互拾取的到时差值为-1.25—1.49 s, 平均绝对差值为(0.388±0.341) s, 绝对差值在0.2 s, 0.3 s和0.5 s以内的分别占37.25%, 53.75%和71.5%. 这表明,在初至不清晰的情况下, 3种方法自动识别近震P波震相的效果均不如初至清晰时好, 其中本文小波包-峰度AIC方法拾取的P波精度相对高一些, 峰度AIC方法和STA/LTA方法的精度相对较低, 反映了在人工震相识别中同样面临的当P波初至不清晰时震相识别精度不高这一难题.

图9 初至不清晰时P波震相自动识别与人机交互识别结果对比图中数值分别为3种方法得到的平均绝对差值. (a) STA/LTA方法;(b) 峰度AIC方法; (c) 小波包-峰度AIC方法
Fig.9 Comparison of the P-wave onset time result by automatic recognition with that by man-machine interaction recognition on the condition that the first break is unclear The average absolute errors of the three methods are also given. (a) STA/LTA method;(b) Kurtosis-AIC method; (c) Wavelet packet and Kurtosis-AIC method

图10 初至不清晰时P波震相自动识别与人机交互识别差值分布(a) STA/LTA方法; (b) 峰度AIC方法; (c) 小波包-峰度AIC方法
4 讨论与结论
本文提出了一种基于小波包和峰度AIC的P波震相自动识别方法. 在加权STA/LTA方法粗略拾取P波到时的基础上, 利用该方法进一步拾取精细的P波到时并将其应用于模拟事件的理论地震记录, 模拟事件参照云南地区实际震例设计. 对理论地震记录加入不同信噪比的高斯白噪声和实际地震噪声, 以由射线追踪技术得到的到时为标准, 对比了STA/LTA方法、 峰度AIC方法和本文的小波包-峰度AIC方法自动识别P波的效果(表1和表2). 结果表明, 本文方法具有更强的抗噪能力, P波识别的精度更高, 当加入实际地震噪声的SNR≥8 dB时, 其自动拾取与理论计算的P波差值在0.25 s以内.
将本文方法应用到云南地区722个单台垂直向实际地震记录中, 滤波前自动拾取与人机交互拾取的P波差值部分过大(图5b), 这是由于原始记录信噪比低或初至不清晰而造成的; 通过本文FIR最佳频带方法自适应滤波后, 大大提高了原始记录的信噪比和P波拾取的精度. P波初至识别差值、 信噪比和初至清晰度关系(图6)的分析结果表明: 初至清晰时信噪比较高, 但信噪比高时初至却并不一定清晰; P波自动拾取的精度与信噪比有一定关系, 但并非是信噪比越高P波初至识别差值越小的线性关系, 相对信噪比对其的影响, 初至清晰度对其的影响更大, 且初至清晰时到时拾取的精度明显比初至不清晰时高.
将地震记录分为初至清晰和初至不清晰两种情况, 以人工拾取的震相到时为标准, 分别对比STA/LTA方法、 峰度AIC方法和本文方法的效果, 结果表明本文的小波包-峰度AIC方法拾取P波初至的精度更高. 当初至清晰时, 经FIR最佳频带方法滤波后信噪比均大于8 dB, 本文方法自动识别的P波到时与人工识别结果的平均绝对差值为(0.077±0.075) s, 绝对差值在0.1 s和0.2 s以内的分别占73.6%和94.41%, 精度非常高.
鉴于本文研究所选用的地震均为近震事件, 下一步将把本文方法运用到远震事件中进一步检验该方法的效果, 当初至不清晰时P波识别的精度有待于进一步提高.
感谢德国地学研究中心汪荣江博士提供合成理论地震图的计算程序, 感谢Ludger Küperkoch教授提供帮助和有益探讨.
常旭, 刘伊克. 2002. 地震记录的广义分维及其应用[J]. 地球物理学报, 45(6): 839-846.
Chang X, Liu Y K. 2002. The generalized fractal dimension of seismic records and its applications[J].ChineseJournalofGeophysics, 45(6): 839--846 (in Chinese).
刘晗, 张建中. 2014. 微震信号自动检测的STA/LTA算法及其改进分析[J]. 地球物理学进展, 29(4): 1708--1714.
Liu H, Zhang J Z. 2014. STA/LTA algorithm analysis and improvement of microseismic signal automatic detection[J].ProgressinGeophysics, 29(4): 1708--1714 (in Chinese).
刘希强, 周蕙兰, 郑治真, 沈萍, 杨选辉, 马延路. 1998. 基于小波包变换的弱震相识别方法[J]. 地震学报, 20(4): 373--380.
Liu X Q, Zhou H L, Zheng Z Z, Shen P, Yang X H, Ma Y L. 1998. Identification method of weak seismic phases on the basis of wavelet packet transform[J].ActaSeismologicaSinica, 11(4): 431--439.
刘希强, 周蕙兰, 曹文海, 李红, 李永红, 季爱东. 2002. 高斯线调频小波变换及其在地震震相识别中的应用[J]. 地震学报, 24(6): 607--616.
Liu X Q, Zhou H L, Cao W H, Li H, Li Y H, Ji A D. 2002. Gauss linear frequency modulation wavelet transform and its application to seismic phases identification[J].ActaSeismologicaSinica, 24(6): 607--616 (in Chinese).
刘希强, 周彦文, 曲均浩, 石玉燕, 李铂. 2009. 应用单台垂向记录进行区域地震事件实时检测和直达P波初动自动识别[J]. 地震学报, 31(3): 260--271.
Liu X Q, Zhou Y W, Qu J H, Shi Y Y, Li B. 2009. Real-time detection of regional events and automatic P-phase identification from the vertical component of a single station record[J].ActaSeismologicaSinica, 31(3): 260--271 (in Chinese).
毛燕, 崔建文, 郑定昌, 李正光, 卢吉高. 2011. 地震记录的P波自动捡拾[J]. 地震研究, 34(1): 47--51.
Mao Y, Cui J W, Zheng D C, Li Z G, Lu J G. 2011. Automatic P-wave detection of the earthquake recordings[J].JournalofSeismologicalResearch, 34(1): 47--51 (in Chinese).
曲保安, 刘希强, 蔡寅, 范晓勇, 林秀娜, 于庆民, 赵瑞, 李铂, 周彦文. 2014. 近震S波震相实时自动识别方法研究[J]. 地震学报, 36(2): 184--192.
Qu B A, Liu X Q, Cai Y, Fan X Y, Lin X N, Yu Q M, Zhao R, Li B, Zhou Y W. 2014. Method for real-time automatic identification of S-phase: Application to local seismicity[J].ActaSeismologicaSinica, 36(2): 184--192 (in Chinese).
孙进忠, 赵鸿儒, 彭一民. 1985. 全波模型的震相分析[J]. 石油地球物理勘探, 20(4): 352--362.
Sun J Z, Zhao H R, Peng Y M. 1985. Full wave model phase analysis (FPA)[J].OilGeophysicalProspecting, 20(4): 352--362 (in Chinese).
万永革. 2012. 数字信号处理的MATLAB实现[M]. 第2版. 北京: 科学出版社: 298--322.
Wan Y G. 2012.DigitalSignalProcessingBasedonMATLAB[M]. 2nd ed. Beijing: Science Press: 298--322 (in Chinese).
王海军, 靳平, 刘贵忠, 王晓明. 2003. 区域震相初至估计[J]. 西北地震学报, 25(4): 298--303.
Wang H J, Jin P, Liu G Z, Wang X M. 2003. Accurate estimation for arrival time of seismic wave[J].NorthwesternSeismologicalJournal, 25(4): 298--303 (in Chinese).
王海军, 刘贵忠, 范万春. 2004. 广义分维在地震信号初至检测中的应用[J]. 核电子学与探测技术, 24(6): 634--637.
Wang H J, Liu G Z, Fan W C. 2004. The application of generalized fractal in arrival time detection of seismograms[J].NuclearElectronicsandDetectionTechnology, 24(6): 634--637 (in Chinese).
王继, 陈九辉, 刘启元, 李顺成, 郭飚. 2006. 流动地震台阵观测初至震相的自动检测[J]. 地震学报, 28(1): 42--51.
Wang J, Chen J H, Liu Q Y, Li S C, Guo B. 2006. Automatic onset phase picking for portable seismic array observation[J].ActaSeismologicaSinica, 28(1): 42--51 (in Chinese).
王娟, 刘俊民, 范万春. 2004. 神经网络在震相识别中的应用[J]. 现代电子技术, 27(8): 35--37.
Wang J, Liu J M, Fan W C. 2004. Application of neural network in the discrimination of seismical signal[J].ModernElectronicsTechnique, 27(8): 35--37 (in Chinese).
王喜珍. 2004. 小波变换在地震数据压缩和震相到时拾取中的应用研究[D]. 北京: 中国地震局地球物理研究所: 87--90.
Wang X Z. 2004.StudyonApplicationofWaveletTransforminCompressingSeismicDataandPickingtheOnsetTimeofSeismicPhase[D]. Beijing: Institute of Geophysics, China Earthquake Administration: 87--90 (in Chinese).
武东坡. 2004. 震相识别的实时方法研究[D]. 哈尔滨: 中国地震局工程力学研究所: 11--22.
Wu D P. 2004.ResearchontheReal-TimeProcessingMethodofSeismicPhaseIdentification[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration: 11--22 (in Chinese).
杨配新, 邓存华, 刘希强, 任勇, 颜其中. 2004. 数字化地震记录震相自动识别的方法研究[J]. 地震研究, 27(4): 308--313.
Yang P X, Deng C H, Liu X Q, Ren Y, Yan Q Z. 2004. Studies on auto-distinguishing phase of digital seismic recor-dings[J].JournalofSeismologicalResearch, 27(4): 308--313 (in Chinese).
赵爱华, 张中杰, 彭苏萍. 2003. 复杂地质模型转换波快速射线追踪方法[J]. 中国矿业大学学报, 32(5): 513--516.
Zhao A H, Zhang Z J, Peng S P. 2003. Fast ray tracing method for converted waves in complex media[J].JournalofChinaUniversityofMining&Technology, 32(5): 513--516 (in Chinese).
赵大鹏, 刘希强, 李红, 周彦文. 2012. 峰度和AIC方法在区域地震事件和直达P波初动自动识别方面的应用[J]. 地震研究, 35(2): 220--226.
Zhao D P, Liu X Q, Li H, Zhou Y W. 2012. Detection of regional seismic events by Kurtosis method and automatic identification of direct P-wave first motion by Kurtosis-AIC method[J].JournalofSeismologicalResearch, 35(2): 220--226 (in Chinese).
赵鸿儒, 孙进忠, 唐文榜. 1990. 全波震相分析的应用[J]. 地球物理学报, 33(1): 54--63.
Zhao H R, Sun J Z, Tang W B. 1990. The application of full wave phase analysis[J].ChineseJournalofGeophysics, 33(1): 54--63 (in Chinese).
庄东海, 肖春燕, 颜永宁. 1994. 利用人工神经网络自动拾取地震记录初至[J]. 石油地球物理学报, 29(5): 659--664.
Zhuang D H, Xiao C Y, Yan Y N. 1994. Seismic first arrival pickup using artificial neural network[J].OilGeophysicalProspecting, 29(5): 659--664 (in Chinese).
Allen R. 1978. Automatic earthquake recognition and timing from single trace[J].BullSeismolSocAm, 68(5): 1521--1532.
Allen R. 1982. Automatic phase pickers: Their present use and future prospects[J].BullSeismolSocAm, 72(6B): S225--S242.
Baer M, Kradolfer U. 1987. An automatic phase picker for local and teleseismic events[J].BullSeismolSocAm, 77(4): 1437--1445.
Bai C, Kennett B L N. 2000. Automatic phase-detection and identification by full use of a single three-component broadband seismogram[J].BullSeismolSocAm, 90(1): 187--198.
Boschetti F, Dentith M D, List R D. 1996. A fractal-based algorithm for detecting first arrivals on seismic traces[J].Geophysics, 61(4): 1095--1102.
Cichowicz A, Green R W E, van Zyl Brink A. 1988. Coda polarization properties of high-frequency microseismic events[J].BullSeismolSocAm, 78(3): 1297--1318.
Dai H C, MacBeth C. 1997. The application of back-propagation neural network to automatic picking seismic arrivals from single-component recordings[J].JGeophysRes, 102(B7): 15105--15113.
Jurkevics A. 1988. Polarization analysis of three-component array data[J].BullSeismolSocAm, 78(5): 1725--1743.
Küperkoch L, Meier T, Lee J, Friederich W, EGELADOS Working Group. 2010. Automated determination of P-phase arrival times at regional and local distances using higher order statistics[J].GeophysJInt, 181(2): 1159--1170.
Küperkoch L, Meier T, Brüstle A, Lee J, Friederich W, EGELADOS Working Group. 2012. Automated determination of S-phase arrival times using autoregressive prediction: Application to local and regional distances[J].GeophysJInt, 188(2): 687--702.
Leach Jr R R, Dowla F U, Schultz C A. 1999. Optimal filter parameters for low SNR seismograms as a function of station and event location[J].PhysEarthPlanetInt, 113(1/2/3/4): 213--226.
Maeda N. 1985. A method for reading and checking phase times in auto-processing system of seismic wave data[J].Zisin, 38(3): 365--379.
Saragiotis C D, Hadjileontiadis L J, Panas S M. 2002. PAI-S/K: A robust automatic seismic P phase arrival identification scheme[J].IEEETransGeosciRemoteSensing, 40(6): 1395--1404.
Satriano C, Zollo A, Rowe C. 2008. Iterative tomographic analysis based on automatic refined picking[J].GeophysProsp, 56(4): 467--475.
Sleeman R, van Eck T. 1999. Robust automatic P-phase picking: An on-line implementation in the analysis of broadband seismogram recordings[J].PhysEarthPlanetInt, 113(1/2/3/4): 265--275.
Stevenson P R. 1976. Microearthquakes at Flathead Lake, Montana: A study using automatic earthquake processing[J].BullSeismolSocAm, 66(1): 61--80.
Wang R J. 1999. A simple orthonormalization method for stable and efficient computation of Green’s functions[J].BullSeismolSocAm, 89(3): 733--741.
Wang R J, Wang H S. 2007. A fast converging and anti-aliasing algorithm for Green’s functions in terms of spherical or cylindrical harmonics[J].GeophysJInt, 170(1): 239--248.
Wickerhauser M V. 1992. Acoustic signal compression with wavelet packets[G]∥Wavelets:ATutorialinTheoryandApplication. San Diego, California: Academic Press: 679--700.
Yomogida K. 1994. Detection of anomalous seismic phases by the wavelet transform[J].GeophysJInt, 116(1): 119--130.
Zhang H J, Thurber C, Rowe C. 2003. Automatic P-wave arrival detection and picking with multiscale wavelet analysis for single-component recordings[J].BullSeismolSocAm, 93(5): 1904--1912.
Zhao A H, Zhang Z J, Teng J W. 2004. Minimum travel time tree algorithm for seismic ray tracing: Improvement in efficiency[J].JGeophysEng, 1(4): 245--251.
Automatic identification of P-phase based on wavelet packet and Kurtosis-AIC method

1)EarthquakeAdministrationofHunanProvince,Changsha410004,China2)InstituteofGeophysics,ChinaEarthquakeAdministration,Beijing100081,China
Automatic identification of P-phase is of significance to the study on earthquake location, earthquake warning and structure of deep earth. Combining wavelet packet transform with Kurtosis-AIC (Akaike information criterion) technology, this paper puts forward a new synthetic method named wavelet packet and Kurtosis-AIC method for automatic recognition of first P-phase. Three scales of discrete wavelet packet transforms are applied to decompose and reconstructure the original recordings three seconds before and after the rough P-wave arrival time, which is picked up by weighted STA/LTA (short term average/long term average) method, then the Kurtosis-AIC values of the three-scale reconstruction signal are calculated respectively and superposed together, finally the minimum value of the superposed AIC curve is taken as the first P-wave arrival time. In order to test the new method, it is applied to theoretically synthetic seismograms and real seismic recording for automatic P-phase arrival time detection. Adding white Gaussian noise and real seismic noise to synthetic seismograms with different SNR, the optimal frequency band of adaptive FIR (finite impulse response) digital filtering is used to improve the SNR and P-wave recognition accuracy of the original signals. The results show that, with respect to the impact of SNR, the accuracy of P-wave identification is more affected by the clarity of first break; our method has greater noise immunity and higher P-wave recognition accuracy as compared to the weighted STA/LTA algorithm and Kurtosis-AIC method. When the first break of P-wave is clear, average absolute error of P-phase arrival time between automatic identification based on our method and manual identification is (0.077±0.075) seconds.
P-phase; FIR digital filtering; automatic identification of seismic phase; wavelet packet and Kurtosis-AIC method
国家自然科学基金(40974050, 41374098)资助.
2015-05-15收到初稿, 2015-08-17决定采用修改稿.
e-mail: ahzhao123@yahoo.com
10.11939/jass.2016.01.007
P315.3+1
A
田优平, 赵爱华. 2016. 基于小波包和峰度赤池信息量准则的P波震相自动识别方法. 地震学报, 38(1): 71--85. doi:10.11939/jass.2016.01.007.
Tian Y P, Zhao A H. 2016. Automatic identification of P-phase based on wavelet packet and Kurtosis-AIC method.ActaSeismologicaSinica, 38(1): 71--85. doi:10.11939/jass.2016.01.007.

