折纸超材料折展稳态特性研究1)

王海瑞 申薛靖 王宙恒 贾 璐 李传檑 朱龙基 赵丹阳

* (清华大学航天航空学院,北京 100084)

† (西安交通大学机械结构强度与振动国家重点实验室,西安 710049)

** (大连理工大学机械工程学院,辽宁大连 116024)

引言

随着可穿戴设备自感知传感、飞机自适应智能蒙皮、军事装甲多元防护等前沿科技的迅速发展,传统材料的多功能化及变形调控的难度越来越大,通过巧妙的结构设计发展能够突破传统材料性能瓶颈的超材料,已成为新材料研发的重要方向[1-3].折纸超材料作为一种革命性新材料,其在可延展柔性电子[4]、血管支架[5]、高灵敏度传感器[6]、可重构机器人[7-8]及轻量化重大装备[9-10]等方面具有巨大应用前景,因而备受国内外学者的关注,这得益于其内部折纸胞元的丰富设计和大折展比.同时这类材料还拥有变形可重构、功能可编程、尺寸与组分材料独立等优点[11-14],这使得折纸超材料的力学性能不仅呈现出优异的可调性能,而且具有广阔的调控裕度.

折纸超材料是通过自身内部微结构连续变形来调控整体宏观大变形,使得力学性能发生演化,例如可调的泊松比、可转变的稳态和多刚度、可变的模量等[15-17].其中最重要也是最独特的力学性能当属折纸构型的多稳态特性.多稳态结构在其运动过程中有多个力学平衡位置,可通过外界能量的输入使结构在不同稳态构型之间跃迁.目前围绕折纸超材料的性能分析研究已经取得了一定进展.Yasuda等[18-19]发现了刚性可动的Tach-Miura 折纸结构在轴向伸缩变形过程中的多稳态特性.Hanna 等[20-21]采用能量原理研究了Waterbomb Origami 构型,发现该构型具有双稳态特性.Silverberg 等[22-23]通过弹性面假设研究了Miura-ori 折纸超材料,发现其存在两种稳定构型其刚度具有再编程性.Cai 等[24-25]分析了Kresling 管轴向伸缩过程中非线性载荷位移曲线,发现典型双稳态特征与初始几何参数条件有关.Fang等[26-29]研究了Miura 堆叠体动力特性,发展了单元的刚度异步自锁,实现了分段多刚度调控.Song 等[30]研究了堆叠的Miura 折纸超材料的渐进能量吸收性能.以上研究围绕Miura 类相对简单的折纸构型及其堆叠体的性能分析取得了一定进展.然而,Miura折纸结构以外具有复杂构型的折纸超材料的构筑较少,稳态等性能研究相对较弱,从而在一定程度上制约了新型超材料的性能调控设计.最近,Wang 等[31]构筑了一种具有三维负泊松比的单层折纸超材料,通过结构参数调控可以使得该结构呈现双重负泊松比.然而,对该折纸超材料性能的深入研究尚且缺乏,难以指导该超材料结构设计及其性能调控.

本文针对新型折纸超材料力学特性不明确的问题,采用折痕等效扭转弹簧分析法和能量原理等方法,推导折纸超材料在折展变形过程中的外载荷与结构参数之间的内在关系,分析在复杂内部构型及折展特征协同作用下的外载荷变化规律,以明晰折纸超材料的稳态特性与折展变形之间关系,为超材料的构型参数优化设计和折展变形中的稳态性能调控提供理论依据.

1 折纸超材料构型与力学模型

图1 所示的折纸超材料属于单自由度刚性折纸构型,是由多个面体通过公共折痕连接组成.从三维模型可以看出,该构型存在内凹几何特征,使其呈现三维(面内和离面方向)负泊松比特性.其中图1(a)所示的折痕图展示了包括间距尺寸比(r)、边长比(p,q)和内角(α)以及与初始折展状态相关的初始折展角(θ0)等几何参数.如图1(b)所示,在准静态折展过程中,假定折纸构型的折痕为扭力弹簧,其单位长度刚度为k.因此,外载荷在其作用方向上所做的外功能够全部转化为超材料内部折痕的弹性势能.

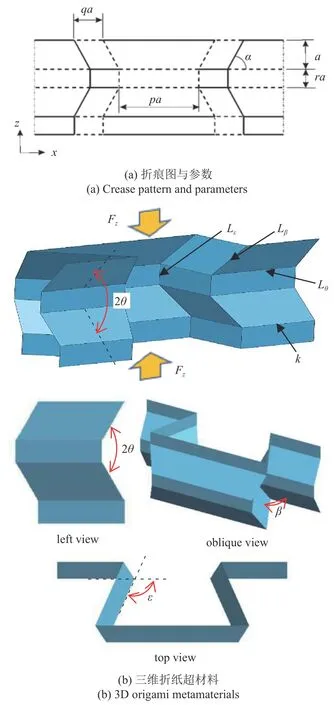
图1 折纸超材料单胞的折痕图及三维构型Fig.1 Crease pattern and 3D configuration of origami metamaterials

折纸构型的初始高度对应于其初始折展角度 θ0.外载荷作用下的位移为s.此时,折纸超材料在外载荷Fz作用下产生的外功为

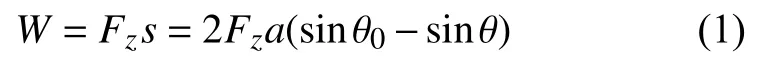
同时,折纸超材料在准静态折展过程中所有折痕存储的势能为

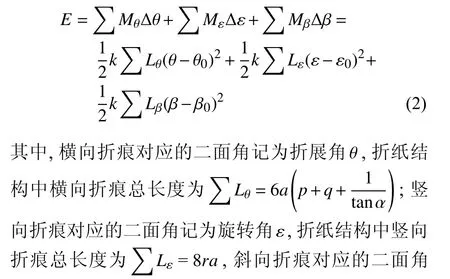
折纸超材料在折展变形过程中的总能量为U=E-W.由于超材料变形过程中始终处于平衡状态,以折展角 θ 为自变量,根据最小势能原理=0 .同时结合文献[31]中折纸超材料的二面角和旋转角与折展角的关系,可以求得折纸超材料单胞在折展过程中的外载荷为

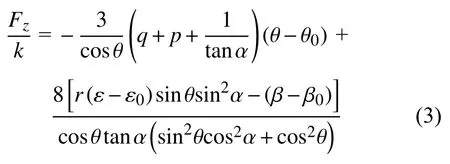
从外载荷公式可以看出,折纸超材料的外载荷为结构几何形状与初始折展状态的函数.为揭示折纸超材料在折展过程中的稳态行为,有必要进一步探索上述结构参数对折展外载荷的影响规律.

2 参数影响规律分析

本文选定尺寸比a=1,p=5 为折纸超材料长度基准,通过分析折展过程中外载荷的变化规律,研究超材料的稳态特性.图中色差带分别表示外载荷的正负和大小.外载荷的正负边界是初始折展角 θ0.当折展角 θ从初始 θ0增加到90°时,超材料为展开变形,此时为拉伸外载荷,定义为负值.当折展角 θ从 θ0减小到0°时,超材料为折叠变形,此时为压缩外载荷,定义为正值.同时外载荷的增减过程分别对应了正刚度和负刚度.

2.1 边长比对折纸超材料外载荷的影响

图2(a) 显示折叠压缩外载荷与折展角θ负相关.图2(b) 显示压缩外载荷先增大到最大值(黑色虚线),然后减小到最小值(红色点划线),最后略有增加,即呈现双稳态特性.图2(c)显示压缩外载荷首先增加到最大值(黑色虚线),然后逐渐减小,表现出单稳态特性.

从图2 中可以看出,为避免极限折叠时折纸结构的自干扰,横坐标边长比q的范围取决于结构的边长比p和内角α.此外当折展角 θ 固定时,折纸超材料的折展外载荷与边长比参数q呈正相关性.从图2(a)～图2(c)的对比可以看出,内角α 的增加促使双稳态的出现.间距尺寸比r的增加使得双稳态转变为单稳态.这表明稳态间的转变与内角α 和间距尺寸比r有关.

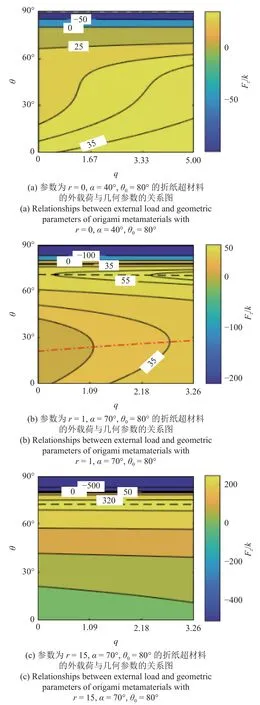
图2 折纸超材料在折展过程中外载荷 Fz/k与边长比q之间的关系Fig.2 Relationships between external load Fz/kand edge ratio qduring the folding of origami metamaterials

2.2 内角对折纸超材料外载荷的影响

图3(a)显示折叠压缩载荷与折展角θ负相关,与内角α也是负相关;展开拉伸外载荷与内角α负相关.图3(b)显示压缩载荷表现出多种情况,内角α在0°～ 45°范围内,折叠压缩载荷单调增加;内角α在45°～ 73.2°范围内,折叠压缩载荷先快速增加,然后减少,最后缓慢增加,即压缩载荷呈现双稳态.图3(c)显示折叠压缩载荷在内角α为0°～ 24°范围内表现为单调性,在内角α为24°～ 32°范围内表现为双稳态,在内角α为32°～ 73.2°范围内表现为单稳态.以上表明,折纸构型的外载荷稳态特性与内角α密切相关.

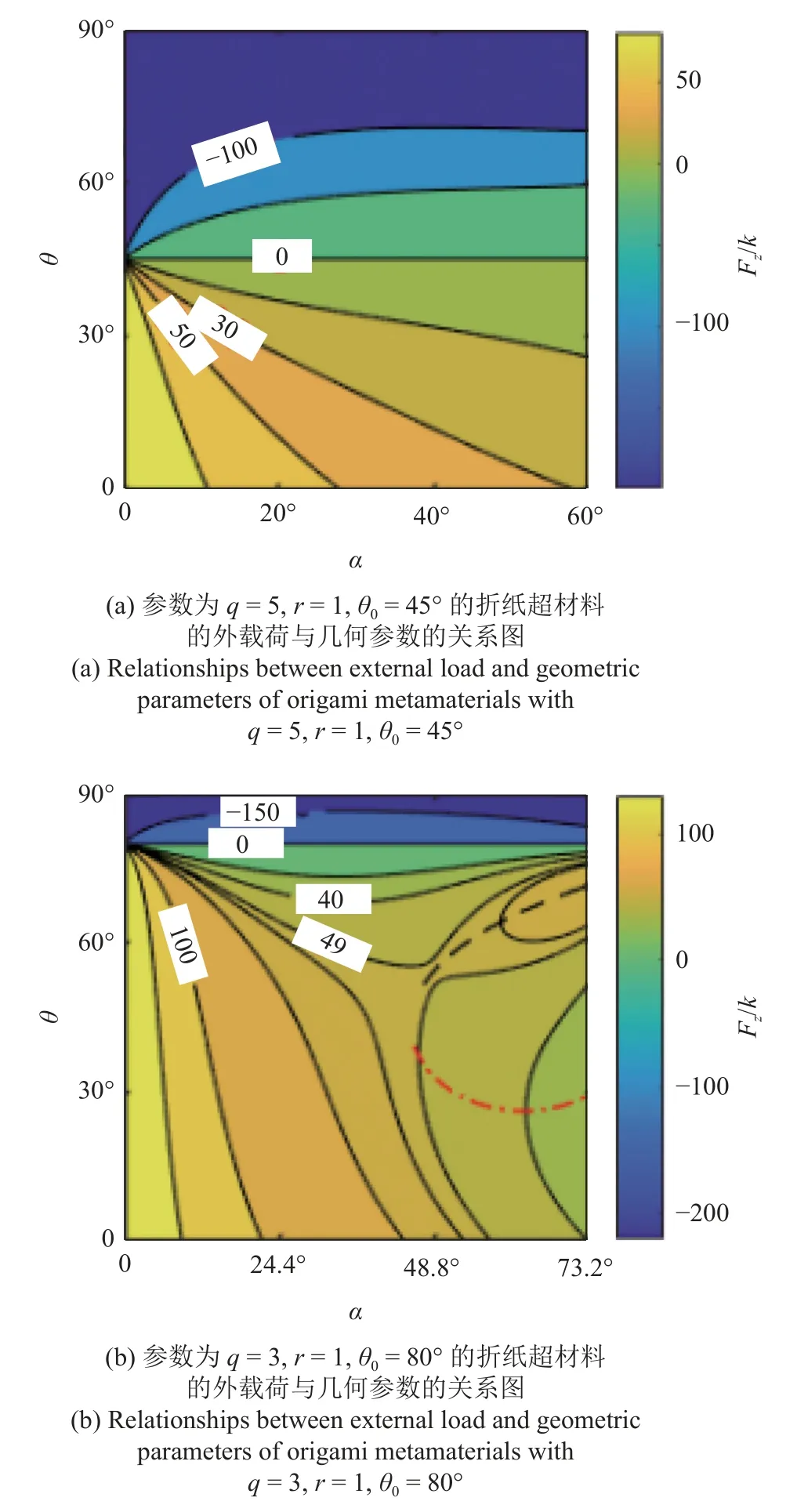
图3 折纸超材料在折展过程中外载荷 Fz/k与折展角 α 之间的关系Fig.3 Relationships between external load Fz/kand inner angleα during the folding of origami metamaterials

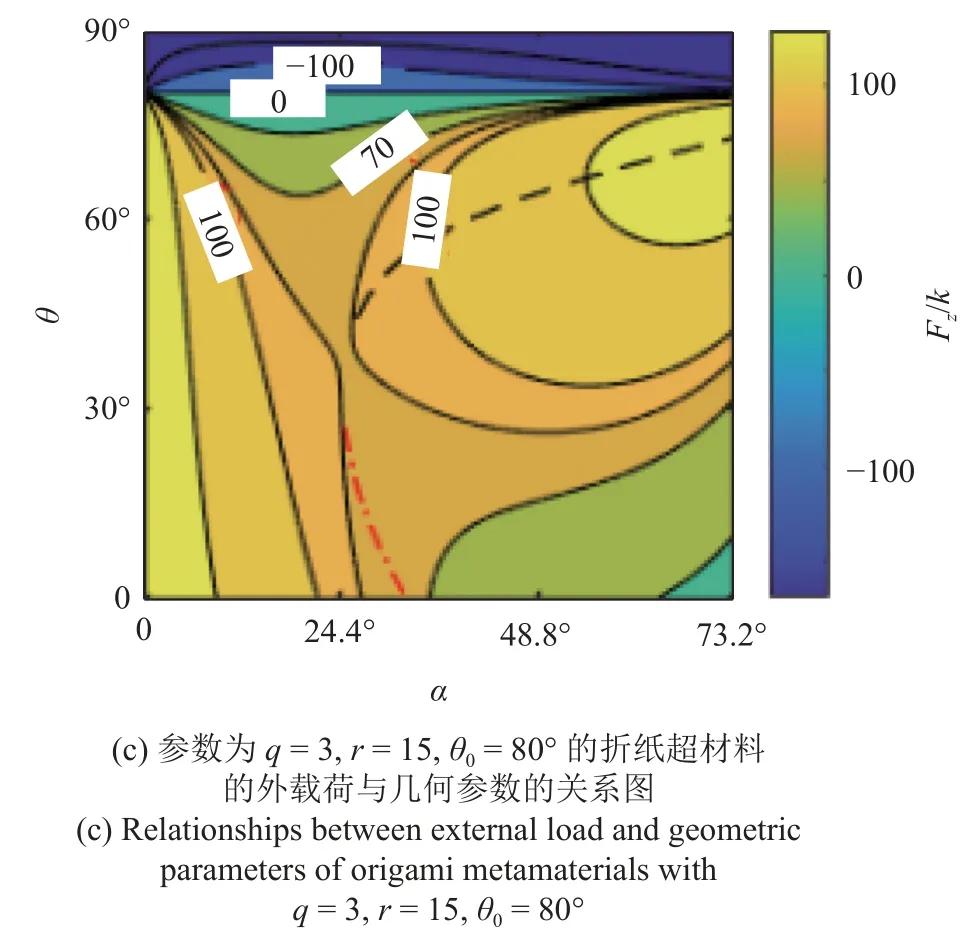
图3 折纸超材料在折展过程中外载荷 Fz/k与折展角 α 之间的关系(续)Fig.3 Relationships between external load Fz/kand inner angleα during the folding of origami metamaterials (continued)

从图3 中可以看出,展开拉伸外载荷与折展角θ呈负相关;为避免极限折叠时折纸结构的自干扰,横坐标内角α的取值范围决定了边长比参数q的取值.从图2(a)～图2(c)之间的比较可以看出,随着初始折展角度 θ0的增加,压缩外载荷逐渐表现出稳态特性;而随着间距尺寸比r的增大,外载荷表现出由双稳态向单稳态的转变,且稳态范围增大.这表明,初始折展角 θ0和间距尺寸比r对压缩外载荷稳态的影响非常显著.

2.3 间距尺寸比对折纸超材料外载荷的影响

图4(a)显示随着间距尺寸比r或折展角 θ 的变化,压缩外载荷始终呈现单调性,即无稳态.图4(b)显示压缩外载荷在间距尺寸比r为0～ 6.3 范围内单调增加,即无稳态.在间距尺寸比r为6.3～ 7.2 和12.9～ 15 的范围内,压缩外载荷表现出单稳态特性.在间距尺寸比r为7.2～ 12.9 的范围内,压缩外载荷表现出双稳态特性.图4(c)显示压缩外载荷表现出单稳态和双稳态等两种情况,这取决于间距尺寸比r的取值.

从图4 可以看出,当折展角 θ 固定时,随着间距尺寸比r的增加,外载荷逐渐增大;横坐标间距尺寸比r的取值范围与其他几何参数无关,呈现出独立性.从图4(a)和图4(b)的比较可以看出,随着初始折展角度 θ0的增加,压缩外载荷表现出稳态特性.从图4(b)和图4(c)的比较可以看出,随着内角α 的增大,压缩外载荷的稳态范围逐渐增大.这表明内角α 和初始折展角 θ0对折纸构型的稳态形式影响较大.

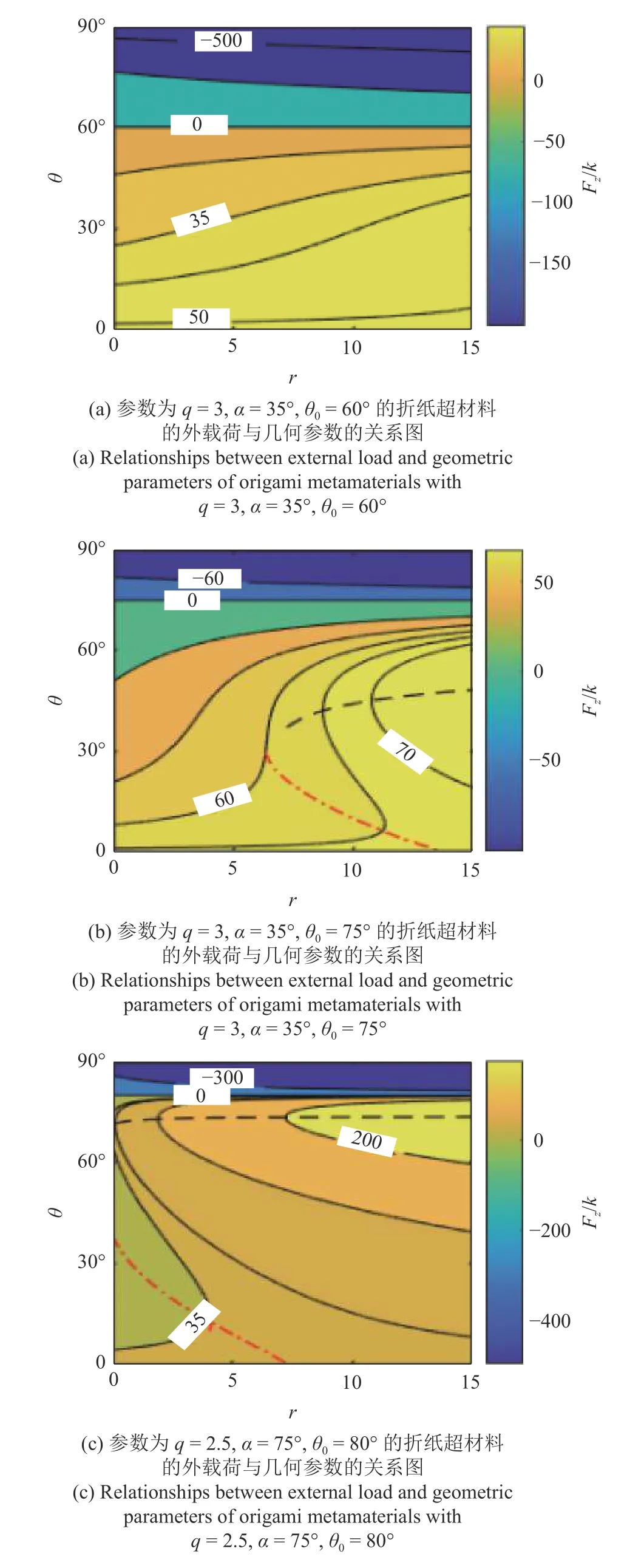
图4 折纸超材料在折展过程中外载荷 Fz/k与间距尺寸比r之间的关系Fig.4 Relationships between external load Fz/kand spacing ratio rduring the folding of origami metamaterials

2.4 外载荷变化规律

从图5 中可以看出,构型参数为p=50,q=18.75,r=5,a=12.5,α=40o,θ0=60o的折纸超材料外载荷在折展过程中单调递增,即不存在稳态.构型参数为p=50,q=15,r=50,a=12.5,α=55o,θ0=70o的折纸超材料外载荷在折展角 θ 为0°～ 51.7°的范围内递减,表现为单稳态特性,此时为负刚度材料,这在精密仪器的隔振等方面具有潜在应用.构型参数为p=50,q=25,r=5,a=12.5,α=75o,θ0=80o的折纸超材料外载荷在折叠过程中先增加(折展角 θ 从80°到69.75°)后减小(折展角 θ 从69.75° 到49.5°),最后又增加(折展角 θ 从49.5° 到0°),表现为双稳态特性,这在冲击吸能等方面具有潜在应用.

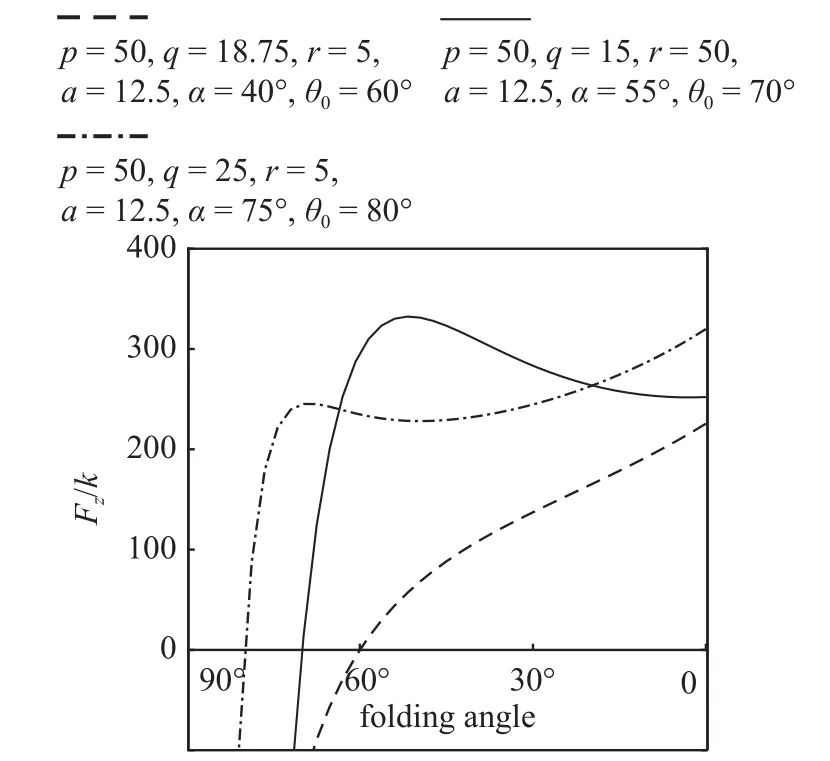
图5 3 种折纸超材料在折展过程中外载荷的变化Fig.5 Three kinds of variations of external loads during folding oforigami metamaterials

综上,所有折纸超材料的外载荷在展开过程中都呈现单调性.不同折纸超材料的外载荷在折叠过程中表现出不同的变化趋势,从而呈现出单调性、单稳态和双稳态等不同状态.外载荷的稳态特性则由边长比q、内角α、折展角 θ0和间距尺寸比r共同调控.

3 结论

本文理论研究了新型折纸超材料的面内单向准静态折展过程的力学性能,建立了折纸构型折展变形过程的力学模型,获得了折展外载荷与构型几何参数之间的内在关系,得到以下结论.

(1) 该折纸超材料的外载荷在展开过程中呈现单调性,展开外载荷与折展角 θ 负相关.

(2) 外载荷在折叠过程中可以呈现单调性、单稳态和双稳态,这些特性的调控密切依赖于边长比q、内角α、折展角 θ 和间距尺寸比r等构型参数.

(3) 揭示了折纸超材料稳态特性的转变机理.初始折展角 θ0促使压缩外载荷表现出稳态特性;内角α的增加促使双稳态的出现,间距尺寸比r的增加使得双稳态向单稳态转变,且稳态范围增大.

研究结果为新型折纸超材料稳态性能的调控和构型设计提供了可借鉴的思路.有助于推动折纸超材料在大延展皮肤电子、气动可变行飞行器和高强度军事装甲防护等方面的工程应用.