含弹性碰撞作用的双级双稳态结构振动能量采集研究
郝玉涛,苏克玮,杨 恺
(1.北京理工大学宇航学院,北京 100081;2.上海盈蓓德智能科技有限公司,上海 201100;3.华中科技大学航空航天学院,湖北 武汉 430074)
引 言
非线性振子结构在外部激励下具有较大的动能[1],在较宽的频带内具有较大的幅值动态响应。结构动态响应可通过机电转换材料(例如压电材料)转化为电能,因此利用非线性振子作为振动能量采集器是近年来研究的热点[1-3]。其中,一种具有双势能阱的非线性振子结构受到研究人员的关注[4-6]。该结构呈现“负刚度”特性,存在两个对称分布的稳定平衡位置,因此该结构被称为双稳态结构。当受到一定程度的外激励作用,双稳态结构会呈现出特殊的跨阱振动,即振子质量在两个稳定平衡位置间大幅度“跳跃”[7]。这种力学现象有助于提升振动利用的工作带宽,提高结构的振动幅值,进而提高振动能量转换成电能的效率。
国内外学者针对双稳态结构的非线性振动能量采集进行了深入研究。例如,Yang 等[8]和Wang 等[9]研究了基于双稳态压电梁结构的风致振动能量采集机理问题。Zhou 等[10]和Erturk 等[11]研究了磁致双稳态压电结构的能量采集性能,并给出了拓宽跨阱振动带宽的结构改进措施。Cai 等[12]研究了双稳态梯形压电能量采集装置的优化问题,提出通过参数优化提高振子的跨阱振动特性,以此提升能量采集性能。
另一方面,有学者发现引入弹性碰撞机制可以有效改善双稳态振子的振动特性[13-14]。例如蓝春波等[13]在双稳态压电梁和结构框架上引入弹性碰撞,提高了振子的跨阱振动性能;Zhou 等[14]在结构边框上增加一个弹簧小球结构,使双稳态压电梁端部能与弹簧小球发生碰撞,进而提升双稳态压电梁的能量采集性能。然而,这些研究工作仅考虑单自由度双稳态结构与固定支架之间的弹性碰撞,而没有研究弹性碰撞对双级双稳态结构的动力学影响。有学者研究发现,在双稳态结构系统中引入额外的线性自由度组成串联结构,能进一步强化双稳态结构的跨阱振动响应,从而有利于提升结构的振动能量采集效率。例如,Harne 等[15]和Wu 等[16]研究了一种由线性结构和双稳态非线性结构组成的双级双稳态能量采集器,并通过实验验证了附加线性自由度对双稳态跨阱振动响应的提升作用。本课题组详细研究了两种组合形式的双级双稳态结构非线性振动行为,进一步验证了双自由度结构形式能够显著增强跨阱振动响应的带宽和振幅[17-18]。这些研究工作预示,若将弹性碰撞引入双自由度双稳态结构,将能够结合弹性碰撞和双自由度两种优势,提升双稳态非线性结构的跨阱振动特性,提高振动能量采集效率。
受上述文献的研究工作启发,本文提出一种含弹性碰撞作用的双级双稳态结构(以下简称“碰撞双级双稳态结构”)。碰撞双级双稳态结构是由双稳态非线性级和线性级组成的双级两自由度结构。其中,双稳态级采用斜拉弹簧引入双稳态非线性弹簧恢复力,并通过在该级中心线两侧的振子运动轨道上分别布置弹簧引入弹性碰撞作用。通过该碰撞作用,将显著增强双级双稳态结构的大幅度跨阱振动响应,改进双级双稳态结构的振动能量采集性能。本文将建立碰撞双级双稳态结构的机理模型,并通过实验和数值仿真等方法,深入讨论该结构的非线性动力学特性,揭示弹性碰撞距离和布置的对称性对系统性能的影响规律。
1 基本原理
1.1 结构模型
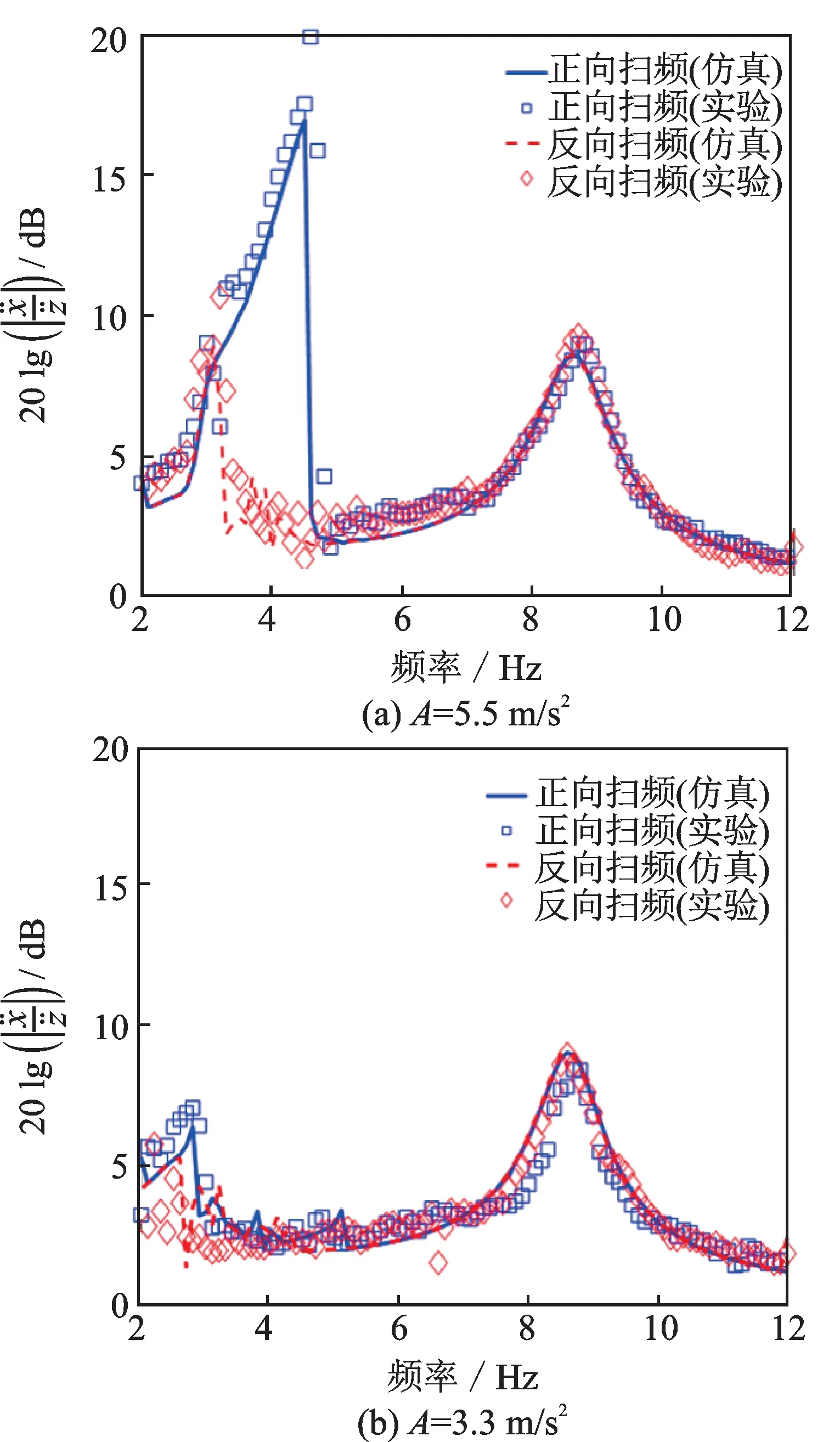
图1给出含弹性碰撞作用的双级双稳态结构。碰撞双级双稳态结构是由双稳态非线性级和线性级组成的两自由度串联结构。双稳态非线性级由一个含磁铁的动子m1,斜置弹簧(刚度为k0,原长为l0)组成。动子m1可在布满线圈的轨道上沿图示水平方向做往复运动,从而通过电磁感应原理将动能转换成电能,实现能量采集。动子m1水平方向尺寸为2l,斜置弹簧与动子的连接位置位于动子上表面的中心。斜置弹簧与双稳态非线性级框架的连接位置到弹簧与动子连接位置的垂直距离为h0。通过调整h0,使得h0 图1 含弹性碰撞的双级双稳态结构模型Fig.1 The schematic of the dual-stage bistable structure with the elastic collision 当碰撞双级双稳态结构的基座发生振动时,会分别激起双稳态级和线性级的振动,导致动子m1在布满线圈的轨道上振动。该振动通过电磁感应转换成电流,并加载在负载电阻RL上,完成能量采集过程。该结构分别利用双自由度结构和弹性碰撞两个物理机制,增强系统的跨阱振动响应(即增强m1往复跨越中心线的大幅度振动响应),以提高能量采集效率。 根据图1所示的结构模型,系统动能为: 系统势能为: 耗散函数为: 广义力做功为: 式中x为动子m1偏离中心线的位移,y为弹簧k2的形变位移,z为基座振动激励位移,c1为m1运动过程中受到的线性阻尼系数,Γ为电磁转换系数(单位线圈电流产生的电磁作用力),I为电流,Fimpact为弹性碰撞引起的等效碰撞作用力: 利用含耗散函数的拉格朗日方程可推导出碰撞双级双稳态结构的振动力学方程。方程表达式如下: 设线圈的电感为L、内阻为R,则线圈连接负载电阻RL上,满足如下电学方程: 振动能量采集的功率为: 在后续的机理研究之前,通过实验验证式(6),(7)中的双级双稳态结构的主体力学模型。实验装置如图2所示,双级双稳态结构装置安装在激振器上,通过激振器使结构基座产生持续加速度激励,即=Asin(2πΩt)。采用加速度传感器测量激励、m1和m2的振动,实验结构中无线圈和无弹性碰撞,因此Γ=0,Fimpact=0。采用扫频加速度激励:Ω=2~12 Hz,扫频速度为0.025 Hz/s。激励幅值分别为:A= 5.5 m/s2和3.3 m/s2。实验参数如下:m1=0.092 kg,m2=0.737 kg,双稳态级固有频率ω0=,损耗因子γ1=c1(m1ω0)≈0.05,线性级固有频率损耗因子γ2=c1(m2ω2)≈0.11。l0=0.098 m,h0=0.096 m。 图2 实验装置Fig.2 Experimental setup 实验和仿真对比结果如图3所示。图3(a)的激励幅值A= 5.5 m/s2,图3(b)的激励幅值A= 3.3 m/s2。其中,正向扫频表示激励频率Ω从2 Hz 逐步变为12 Hz,而反向扫频则是从12 Hz 变为2 Hz。纵坐标为动子m1的加速度幅值与激励幅值的传递比(dB)。传递比越大,表明能激发更大的动子振动,从而有利于振动能量采集。结果显示,仿真和实验结果吻合度高,实验验证了双级双稳态结构的动力学方程。对于两种激励而言,均存在两个明显的峰值区域,例如在图3(a)中,2~6 Hz 出现第一个峰值区域,8~10 Hz 出现第二个峰值区域。采用正向扫频激励,能明显激发第一个峰值区域的振动,导致该区域的振动响应幅值高于反向扫频。这表明正向扫频更容易激发系统的大幅度振动,有利于能量采集。因此,在本文的后续章节中,仅考虑正向扫频结果。 图3 无碰撞双级双稳态结构的仿真和实验对比结果Fig.3 Simulation and experimental comparison results of collision-free dual-stage bistable structure 另一方面,激励幅度越大,越有利于增大低频峰值区域的振动响应。图3(a),(b)结果显示,对于无碰撞的双级双稳态结构而言,需要通过提高激励幅值才能提高动子m1的振动,继而在低频峰值区域获得有效的振动能量采集效率。为使双级双稳态结构能在低幅值激励下同样具有高效的振动能量采集效率,本文将在后续几节详细讨论弹性碰撞对双级双稳态结构振动能量采集性能的提升作用。 图4分别给出在2~12 Hz 正向扫频激励下碰撞双级双稳态结构、不含碰撞的双级双稳态结构以及单级双稳态结构的输出功率。单级双稳态结构为图1中不含线性级(m2,k2,c2)的部分。其中,图4(a)的激励幅值A= 5.5 m/s2,图4(b)的激励幅值A=3.3 m/s2。仿真中所用参数与实验基本相同,其他仿真参数如下:线圈电感L=0.005 H,内阻R=1 Ω,负载电阻RL=5 Ω,弹簧端与中心线的距离b1=b2=0.032 m,碰撞弹簧线性阻尼系数cs1=cs2=0.05 N·s/m,刚度ks1=ks2=1000 N/m,动子几何尺寸l=0.01 m。本文定义有效工作带宽的计算阈值为峰值最大值的25%,即功率超过25%×0.135 W(A= 5.5 m/s2),25%×0.059 W(A= 3.3 m/s2)。结果显示,与传统单级双稳态结构相比,双级双稳态结构拥有更多的大振幅区域,提升了有效工作带宽,同时,双级双稳态结构还显著提升了峰值功率。因此,该结果表明,双级双稳态结构利用两个自由度的耦合作用,显著增强了能量采集性能。当激励幅值A= 5.5 m/s2时,碰撞双级双稳态结构的峰值功率为0.135 W,有效带宽为5.68~9.61 Hz,与无碰撞的双级双稳态结构相比,峰值功率与有效带宽分别增加了48.8%,176.8%。该结果表明,碰撞双级双稳态结构通过引入弹性碰撞,大幅增强了跨阱振动,有效拓宽了工作带宽,提高了振动能量采集性能。当激励幅值A= 3.3 m/s2时,碰撞双级双稳态结构的峰值功率为0.059 W,有效带宽为4.30~9.55 Hz,与不含碰撞的双级双稳态结构相比,峰值功率与有效带宽分别增加了168.2%,1150.0%。该结果表明,通过引入弹性碰撞,提高了系统在研究频段内获得有效振动能量的性能,使双级双稳态结构能在低幅值激励下同样具有高效的振动能量采集效率,提高了结构的能量采集效率和适用范围。 图4 2~12 Hz 正向扫频简谐激励下碰撞双级双稳态结构,不含碰撞的双级双稳态结构和单级双稳态结构的输出功率Fig.4 The power output of the dual-stage bistable structure with the collision mechanism,without the collision mechanism and single-stage bistable structure under 2~12 Hz forward sweep harmonic excitation 为揭示碰撞双级双稳态结构的非线性动力学特性,选取激励幅值A= 3.3 m/s2,Ω=6 Hz(图4中第一个峰值附近的功率),研究不同弹簧端与中心线的距离b1=b2情况下的碰撞双级双稳态结构动力学响应。图5显示激励幅值A= 3.3 m/s2,Ω=6 Hz,b1=b2=0.032 m 时的碰撞双级双稳态结构的相轨迹。在该条件下,结构充分发生碰撞,表现出稳定的大幅度周期跨阱振动(即动子m1在双稳态级两个稳定平衡点间周期振荡),从而显著提高振动能量转换为电能的效率。当进一步增加b1=b2=0.034 m(如图6所示),动子与弹簧之间的距离增大,弹性碰撞具有随机性,结构的跨阱振动响应变得“混乱”,在相轨迹图上表现出混沌现象。图7给出无弹性碰撞的双级双稳态结构动力学响应。可以看出,动子m1的跨阱振动难以被激活,呈现出围绕其中一个稳定平衡点的阱内振动。上述结果表明,引入弹性碰撞作用能够帮助激活双级双稳态结构的大振幅跨阱振动响应,从而提高其振动能量采集效率。 图5 碰撞双级双稳态结构在激励幅值A = 3.3 m/s2,激励频率Ω=6 Hz,b1=b2=0.032 m 下的相轨迹。Fig.5 Phase portrait of the DSBSEC at Ω= 6 Hz,A=3.3 m/s2,b1=b2=0.032 m 图6 碰撞双级双稳态结构在激励幅值A = 3.3 m/s2,激励频率Ω=6 Hz,b1=b2=0.034 m 下的相轨迹。Fig.6 Phase portrait of the DSBSEC at Ω=6 Hz,A=3.3 m/s2,b1=b2=0.034 m 图7 无碰撞双级双稳态结构在激励幅值A = 3.3 m/s2,激励频率Ω=6 Hz 下的相轨迹。Fig.7 Phase portrait of the DSBS without the collision at A = 3.3 m/s2,Ω=6 Hz 为揭示不同弹簧端与中心线的距离b1,b2对系统宽频振动能量采集性能的影响,进行了以下参数研究。在研究过程中,仅改变弹簧端与中心线的距离b1,b2,其他仿真参数仍保持不变。在激励幅值A= 3.3 m/s2时,研究了三种弹性碰撞布置方式:b1=b2=0.028,0.030,0.032 m(距离较小,结构能充分碰撞),b1=b2=0.034 m(结构碰撞出现随机性)和b1=b2=0.036 m(距离较大,结构几乎不发生碰撞)。在2~12 Hz 正向扫频简谐激励下,碰撞双级双稳态结构输出功率随b1,b2的变化如图8所示。结合动力学特性研究结果,当弹簧端与中心线的距离较小时,结构会在较宽的频带内发生周期性碰撞,故而会产生较强的跨阱振动,此时碰撞双级双稳态结构的峰值和带宽均处于较高水平;当结构的碰撞位置处于此范围内时,结构在第一个峰值区域内的峰值与带宽均会随着弹簧端与中心线距离的增大有轻微的提升。当弹簧端与中心线的距离较大时,由于结构难以利用弹性碰撞,结构处于跨阱振动的频带较窄,此时碰撞双级双稳态结构的峰值和带宽均处于较低水平。值得注意的是,在对称布置下,与距离较小的情况相比,在b1=b2=0.034 m 的情况下,结构第二个峰值区域的输出功率几乎没有改变,但其第一个峰值区域的输出功率出现大幅度的降低。研究表明,对称布置下通过调整弹簧端与中心线的距离至0.032 m 附近,可以获得最佳的动力学表现,实现最优的能量采集效果。 图8 在2~12 Hz,对称布置下输出功率随弹簧端与中心线的距离b1,b2的变化Fig.8 Power outputs for differents distance between the center line and the tip of the spring at 2~12 Hz in symmetrical placement 本文研究了弹性碰撞作用对双级双稳态结构振动能量采集的提升作用,得到了以下结论: (1)双级双稳态结构在能量采集方面具有显著的优越性。同时,通过引入弹性碰撞,能显著增强双级双稳态结构的大幅度跨阱振动响应,从而提升系统的振动能量采集效率。其中,针对幅值为3.3 m/s2的基座加速度激励,带宽增加1150.0%(超过10倍),最大功率提升168.2%。 (2)对于3.3 m/s2的基座加速度激励而言,通过引入弹性碰撞,在结构充分发生碰撞时,结构表现出较强的周期性跨阱振动,振动能量转换为电能的效率较高。 (3)参数分析结果显示,存在最优弹性碰撞布置。当弹簧端与中心线的距离b1=b2= 0.032 m时,结构具有较好的能量采集效果。
1.2 振动力学方程

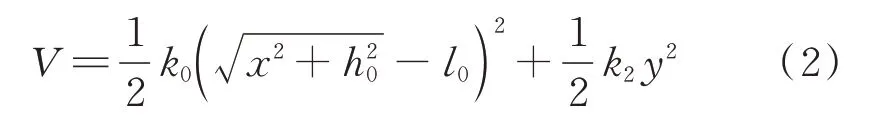




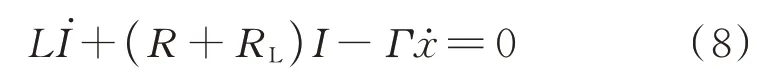

2 双级双稳态结构力学模型的实验验证

3 含弹性碰撞结构的性能对比

4 系统的非线性动力学特性



5 碰撞位置对振动能量采集性能的影响

6 结 论

