复分析Hilbert变换计算理论及非线性检测准则
张 皓,李东升
(1.大连理工大学建设工程学部,辽宁 大连 116024;2.汕头大学工学院,广东 汕头 515063)
引 言
工程结构广泛存在非线性,非线性识别是解决工程结构非线性问题的重要手段。目前,非线性识别的技术框架已经建立[1-2],检测、描述、量化的识别流程基本得到了学术界认可[3-6]。非线性识别的第一步——非线性检测决定了后续工作的走向,因此十分关键。如果工程结构被检测出非线性,继续应用传统线性理论和方法便不再合理,应采用非线性理论和方法进行分析研究。此外,由于损伤会在某种程度上导致结构呈现非线性特征,因此非线性检测方法也可被应用于损伤识别[7-11]。
非线性检测是非线性识别较早发展的内容。判断结构时程响应和频响函数是否具备线性性质自然地成为了非线性检测的基本方法。依据工程经验,直接观察时程响应曲线、频响函数、Nyquist 图等的形状是否产生某种畸变,是非线性检测最简便的方法;其他简便方法如:通过判断在线性结构中时程响应应具备的叠加原理,频响函数应具备的互异性、齐次性法则等是否满足,也可实现非线性检测。实际上,这些简单方法也是线性结构模态分析用于检验试验数据采集质量的常用手段[12]。然而上述简单方法在理论上不够严谨,其实际应用的可靠性也难以保证[1,13]。因此有学者提出了诸多新方法[14]:包括相干函数法、Hilbert 变换法、三阶自相关函数法、高阶频响函数法等,它们具备更强的非线性检测能力。其中,Hilbert 变换法通过检验频响函数进行Hilbert变换前后是否相等来判断非线性是否存在,其数学推导过程严谨,结果可靠;而且,进一步应用Hilbert变换还能够实现非线性的描述和量化,因此得到了广泛关注[15-18]。
Hilbert 变换也是数学界长期关注的问题,但相关研究主要集中在解析求解理论[19]。在进行非线性检测等实际应用时,测试结构的频响函数表达式多为未知,因此需对Hilbert 变换进行数值计算,从而不可避免地引入了截断误差。针对这一问题,一些学者提出了一系列截断误差补偿方法,但是这些方法不仅理论复杂程度远超Hilbert 变换非线性检测方法本身,而且一些方法需借助模态分析理论的机理,应用于非线性结构也不甚合理[13]。文献[1]和[13]引入了一种近似解析方法,它结合了复分析理论和有理逼近理论,有效地解决了Hilbert 变换数值计算截断误差问题;其有理逼近过程理论上可达到任意精度,因此也被称为无截断误差的Hilbert 变换方法。这种方法虽然具有较深奥的数学理论背景,但借助Matlab 等数学计算软件,其实践过程实际上十分简单、明确。令人遗憾地是,国内外学者对此方法似乎仍较为陌生,相关研究和工程应用不仅在国内极为罕见,国外主流研究组近期成果也没有应用此方法,而是对Hilbert 变换截断误差选择了忽略[18]。究其原因,现有的主要参考文献对该方法的介绍有一些模糊之处,这对研究人员的理解和实践可能会造成一定阻碍。本文重新梳理Hilbert 变换复分析计算方法和Hilbert 变换非线性检测方法的数学推导过程,提出通过留数理论补充考虑实轴存在极点的特殊情况,并定义了新的Hilbert 变换非线性检测准则,真正意义上实现两套理论的协调统一,使该方法理论推导更为严谨,体系更为完整,且便于理解和应用,通过数值算例和试验研究验证了该方法的优越性。
1 理论推导
1.1 Hilbert 变换的数学定义及其复分析计算理论
函数f(x) 的Hilbert 变换的数学定义为[19]:
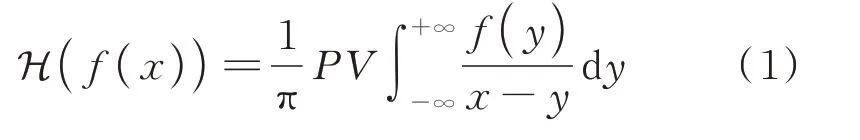
式中 H 表示Hilbert变换算子;PV表示Cauchy主值。
由上式可知,与Fourier 变换、Laplace 变换不同,Hilbert 变换是在同一域内进行的积分变换,其核函数为[19]:
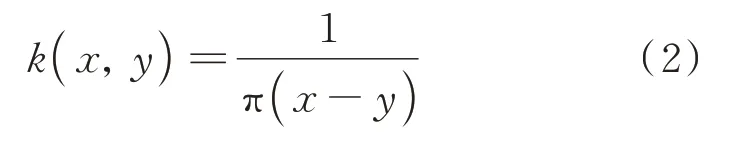
根据式(1)的定义,Hilbert 变换的计算可归结为反常积分的计算问题,复分析理论是解决此类问题的有效工具[20-23]。根据留数定理:设函数f(x)在闭区域D的边界Γ上连续,在这区域的内部,除了有限多个奇点a1,a2,…,an外,处处都解析。那么,如果Γ按正方向(逆时针)绕行,则有[20]:

式中 resf(ak)表示函数f(x)在一个奇点ak处的留数,它是函数f(x)在点ak临域内Laurent 级数展开式的−1 次幂项的系数。
特别地,若此奇点为一阶极点,则函数在此极点的留数为[23]:
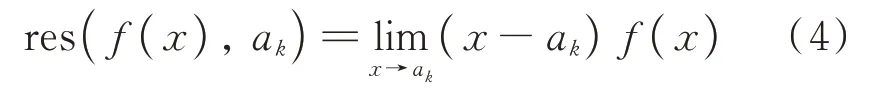
因此,若在复平面补充一段圆弧,则可将式(1)中无限区间的直线积分转化为闭曲线积分,从而可由留数理论求解。不失一般性,考虑上半平面(用“+”脚标表示),若奇点均位于由圆弧ρ和坐标轴(−R,R)直线构成的正方向(逆时针)闭曲线Γ的内部,如图1(a)所示,则此新的路径积分可表示为:
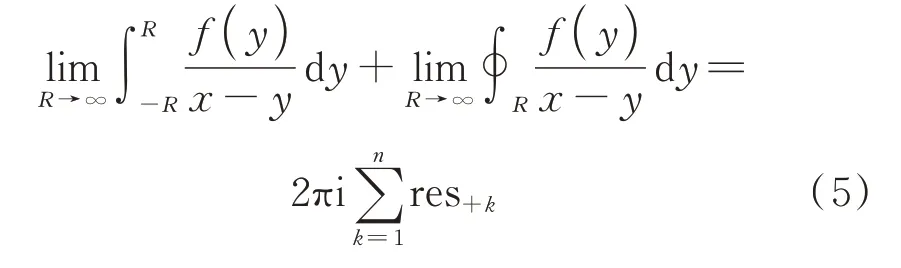
式(5)等号左端第一项即为式(1)中无限区间反常积分的Cauchy 主值[21],是Hilbert 变换计算的主体;第二项根据Jordan 引理可证明为零[22]。假定在闭区域内部有n个奇点,则式(5)右端项中的res+k即为Hilbert 变换被积函数整体在上半平面内奇点k处的留数。将式(5)代入式(1)得到奇点位于闭区域内部时的Hilbert 变换表达式:

应当注意,上述留数定理的运用需满足一个前提条件,即要求函数f(x)在闭区域D的边界Γ上连续。因此,按照上述积分路径,如果实轴上存在奇点(用“0”脚标表示),则无法直接应用式(3)的留数定理计算Hilbert 变换,这也是留数定理本身的一种特殊情况。这种情况的处理办法与奇点位于区域内部类似,即在该奇点临域补充一段半径为r的圆弧路径,如图1(b)所示。按照此新的积分路径,闭区域内部奇点仍可利用式(3)的留数定理,则有:

图1 复平面闭曲线积分路径Fig.1 Closed integral path in the complex plane
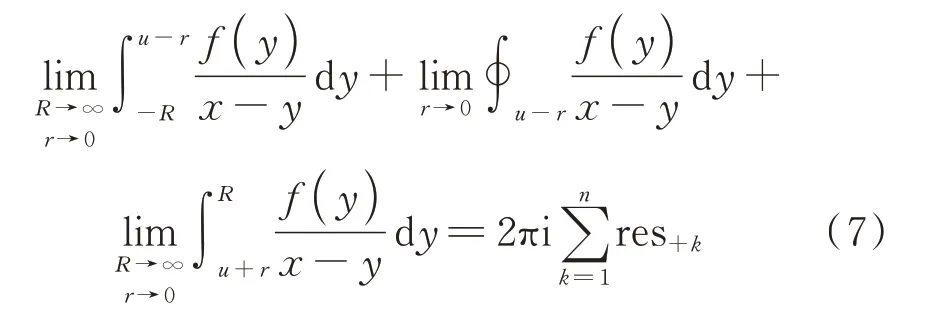
上式等号左端第一项和第三项的直线积分为Hilbert 变换求解目标;如果实轴上的奇点为一阶极点,则第二项曲线积分部分根据小圆弧引理计算[21],且此积分路径下,小圆弧部分为负方向(顺时针)绕行,可得:
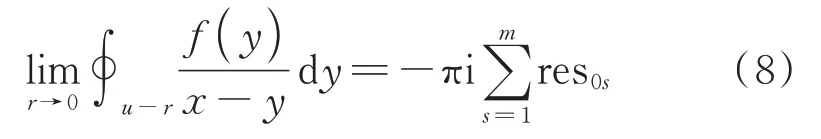
上式右端项中的res0s即为Hilbert 变换被积函数整体在实轴奇点s处的留数。因此,将式(8)代入式(7)并移到等式右端,得到闭区域内部和实轴上均含有奇点,且实轴上的奇点为一阶极点的情况下,Hilbert 变换表达式为:

考虑下半平面(用“−”脚标表示)推导过程类似。若保持直线部分积分路径方向不变,则补充圆弧路径后的闭曲线积分路径为负方向(顺时针),处理实轴极点时添加的小圆弧路径为正方向(逆时针)。因此,下半平面Hilbert 变换表达式为:
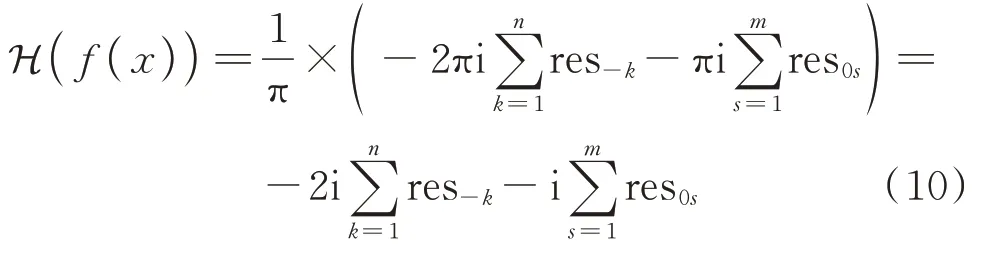
综上,Hilbert 变换的计算实际上就是留数的计算,由函数f(x)奇点的类型决定。以上讨论未指定Hilbert 变换函数f(x)的具体形式,下文将应用上述结论具体讨论对频响函数的Hilbert 变换。另外,未展开讨论有关函数奇点类型的内容,因为其具体应用于频响函数时并不涉及;由于使用了零极点形式,Hilbert 变换被积函数的奇点自然地均为一阶极点,则满足应用小圆弧引理的前提条件,式(9)和(10)必然成立,且留数的计算也比较简单。
1.2 频响函数Hilbert 变换的近似解析计算方法
有理分式逼近具备诸多优良性质,能够解决非线性、高阶、分数阶等复杂函数的逼近问题,相比于多项式逼近具备精度优势[24]。根据逼近理论,任何函数都可以近似为某阶有理分式。因此假定非线性结构的频响函数H(ω)可表示为有理分式并改写为部分分式的形式,即[13]:

式中ω,Cj和pj分别代表频率、零点(在模态分析理论中为留数)和极点。
由于Hilbert 变换是线性积分变换,则频响函数的Hilbert 变换就可以转化为单极点函数的Hilbert变换的和的形式,代入式(1)可得:

此处为了便于理解,传达出Hilbert 变换是在同一域内进行积分变换的内涵,将式(1)中变换函数的自变量x写为频率ω,将式(2)积分变换核函数中的自变量y写为同样常用于表达频率物理意义的符号Ω。这种零极点形式的频响函数有助于Hilbert 变换的计算,因为此时Hilbert 变换被积函数有极点pj,ω为积分变换自由变量且必然不等于pj,否则频响函数部分分式没有意义。因此极点pj为一阶极点,根据式(4)留数的计算方法为:

事实上,即使极点为重极点也有上述类似结论[13]。式(13)暂未指定极点的位置,极点位置一旦明确,即可相应地运用式(6),(9)或(10)进行Hilbert 变换的计算。
运用Matlab 等数学计算软件进行频响函数有理逼近和零极点分解运算时,在上、下半平面和实轴可能同时存在极点。上半平面和实轴的极点使用式(9);下半平面和实轴的极点使用式(10),两者均可计算频响函数的Hilbert 变换,本文取两者的平均值:
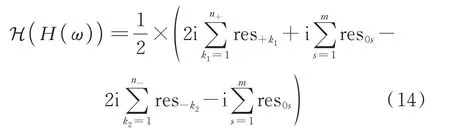
可见,位于实轴的极点部分将在最终的计算公式中抵消。但是,作为计算方法的一部分,有必要加以说明,否则实轴极点该如何操作将成为本方法的一个模糊之处,导致理论理解和实际应用产生阻碍,现有主要参考文献均未进行上述详细讨论[1,13]。将式(13)代入式(14)可得到:

由上式可知,用于计算Hilbert 变换的两个留数求和项,实际上就是零极点形式频响函数极点分别位于上、下半平面的两个部分。因此,频响函数Hilbert 变换的近似解析计算方法最终表达为:
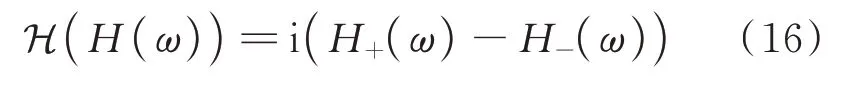
H+(ω)表示极点位于上半平面部分的频响函数,H−(ω)表示极点位于下半平面部分的频响函数。这种方法以近似解析的方式,避免运用梯形公式等数值积分方法计算式(1)中反常积分带来的截断误差,且其推导过程严谨,运算方式十分简单、明确。实际上不只是频响函数,其他能够合理运用有理逼近并进行零极点分解的函数均能推导类似运算方法。站在Riemann-Hilbert 问题这样更为宏大的数学物理视角下,Hilbert 变换的复分析计算方法甚至还有更大的潜力值得开发[25]。
1.3 基于复分析计算理论的Hilbert 变换非线性检测方法
假设线性结构的脉冲响应函数为因果信号h(t),可进行奇偶分解表示为[16]:

式中h(t)偶为偶信号,h(t)奇为奇信号,它们可通过符号函数ε(t)建立起如下关系:

其中符号函数ε(t)为:
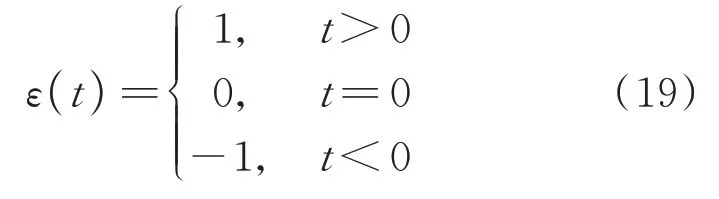
对式(17)两端做Fourier 变换,用符号F 表示,得到变换后的频响函数H(ω)的实部和虚部分别与偶信号和奇信号的Fourier 变换对应,即:

将式(18)代入式(20),根据Fourier 变换的运算法则,得到如下关系:
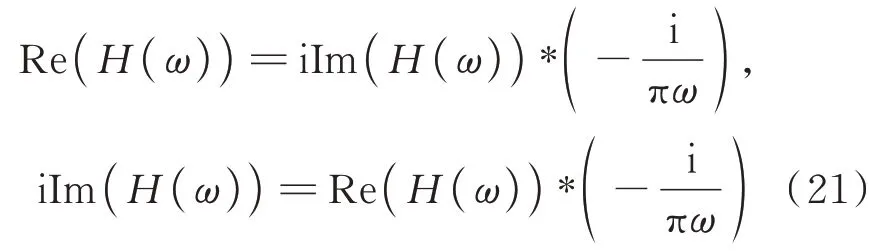
式中 “*”表示卷积运算,由下式定义:

因此,对式(21)进行卷积运算,得到:

上两式直接相加,则在重新组合成H(ω)的同时,有如下关系:
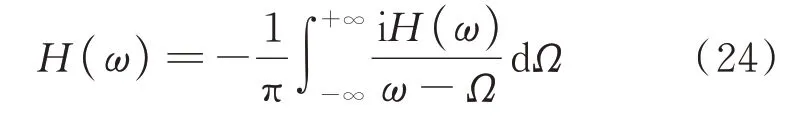
令G(ω) =iH(ω),代入式(16)和(24)得到:
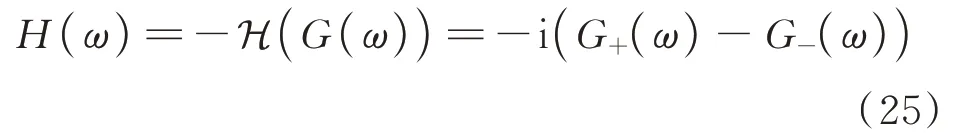
上式两端同时乘以复单位i,可得到最终表达式为:

式(16),(24)~(26)的表达式是一种新的非线性检测理论推导格式,从而形成了式(26)新的非线性检测判据。由于现有运用Hilbert 变换非线性检测方法的文献[1,13]未使用复分析理论,即仅在实轴讨论式(24)中的积分,则可提取复单位i 得到另一种Hilbert 变换的“定义”[13]:

如果同样使用Hilbert 变换符号H 来表达,则将此非线性检测准则表述为[16,26]:
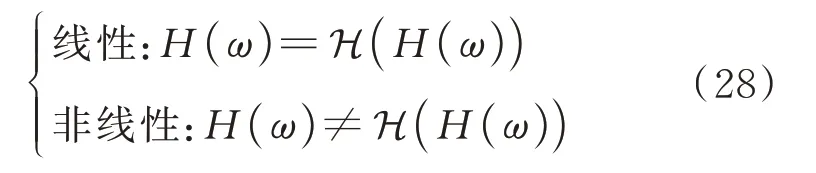
然而,严格地讲,式(27)虽然形式上与式(1)的Hilbert 变换定义很相近,但在数学上式(27)称为Cauchy 变换,它与Hilbert 变换并无等效关系[27];而且按照式(27)推导非线性检测方法实际上并未直接应用Hilbert 变换,因此称其为“Hilbert 变换非线性检测方法”在表面上和实质上都不够严谨。而经过本文的推导,有机结合Hilbert 变换复分析计算理论,才真正意义上使其“名副其实”。现将基于复分析计算理论的Hilbert 变换非线性检测准则表达如下:

值得注意地是,Matlab(R2020b)信号处理工具箱的自带函数Hilbert 实际上计算的是实信号对应的解析信号,而不是其Hilbert 变换,此函数命名的误导性已经在Matlab 官方论坛引起了国内外使用者的讨论。应用此函数针对频响函数进行Hilbert 变换时,即使是线性结构变换前后也不能做到完全一致[26]。
另外,运用上述结论进行非线性检测,实际上隐含了非线性频响函数H(ω)的脉冲响应函数h(t)为非因果信号这一假定。可以推断,若有非线性结构不满足此假定,则此非线性检测方法失效[1]。但目前尚未见相关反例的报告。非线性问题的复杂性决定了建立具有普适意义方法的难度,此假定是否成立应并不影响此非线性检测方法的价值。
2 数值算例
2.1 算例一
首先给出一个数值积分方法直接计算Hilbert变换产生截断误差的典型例子。单自由度线性系统频响函数[13]:
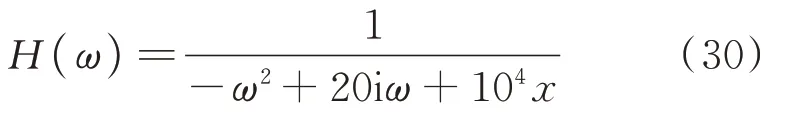
其频率范围为9~23 Hz,频率分辨率为0.1 Hz。运用数值积分方法计算其Hilbert 变换,变换前后的Bode 图对比如图2所示,图中呈现出了明显的截断误差,按照现有式(28)的非线性检测准则,应判断为非线性情况,结论错误。针对同一个频响函数,如果运用复分析计算理论以及本文定义的非线性检测准则,结果极为准确地满足式(29)中规定的线性情况,如图3所示。
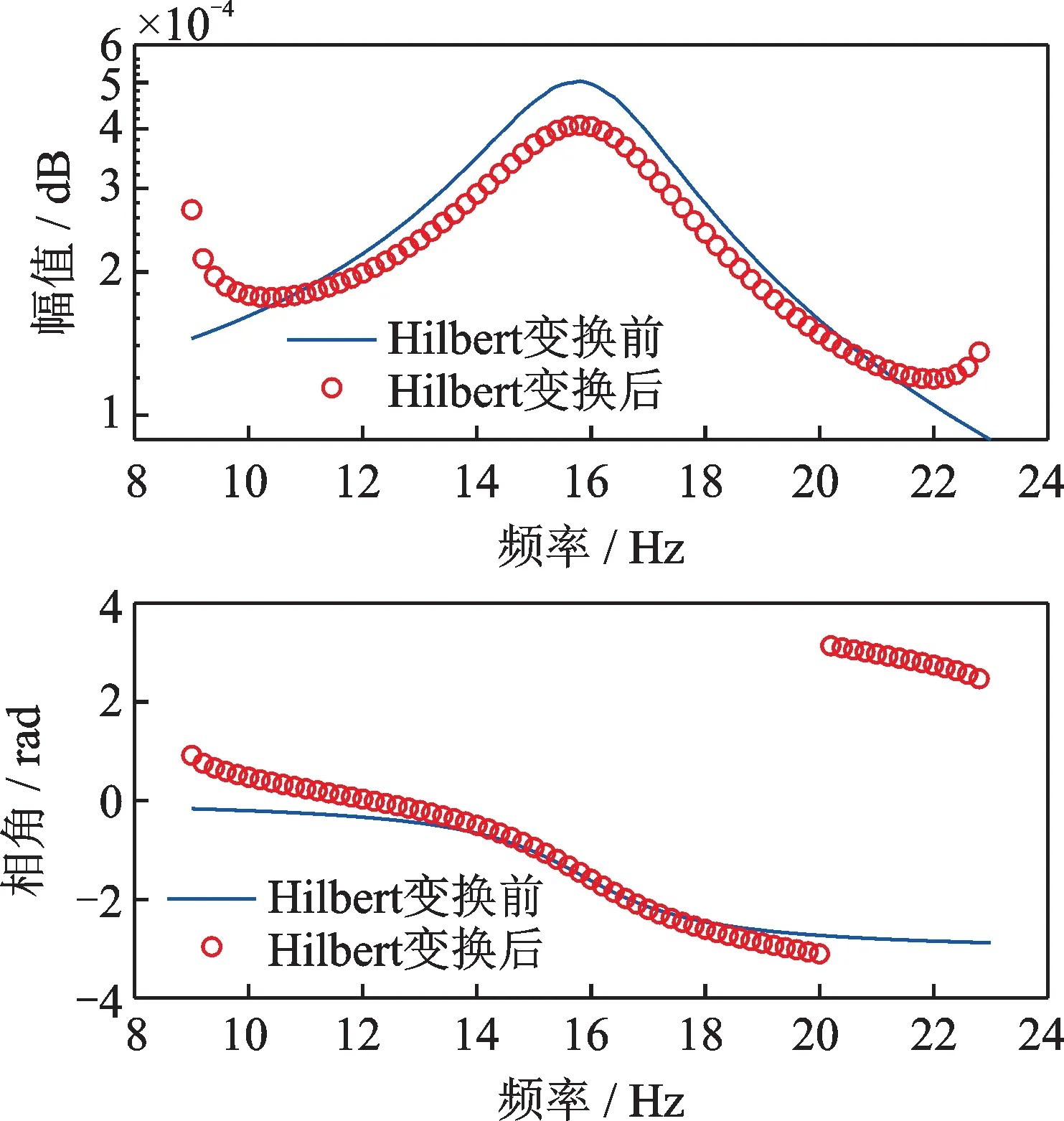
图2 线性系统数值积分Hilbert 变换非线性检测Fig.2 Nonlinear detection results based on numerical integrated Hilbert transform for a linear system
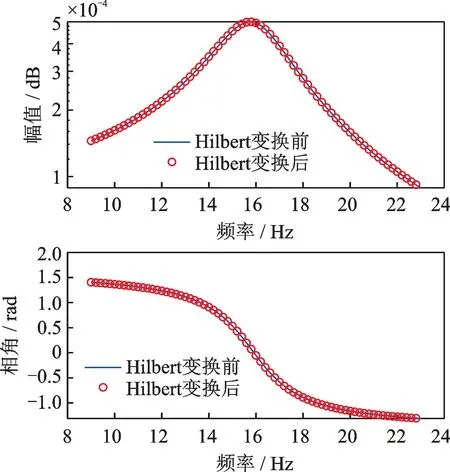
图3 线性系统复分析Hilbert 变换非线性检测Fig.3 Nonlinear detection results based on complex analyzed Hilbert transform for a linear system
2.2 算例二
考虑单自由度非线性系统,在上述线性系统的基础上添加立方刚度项构造Duffing 振子,并在正弦扫频激励条件下得到频响函数,即使用一阶谐波平衡意义下的非线性频响函数[13]:
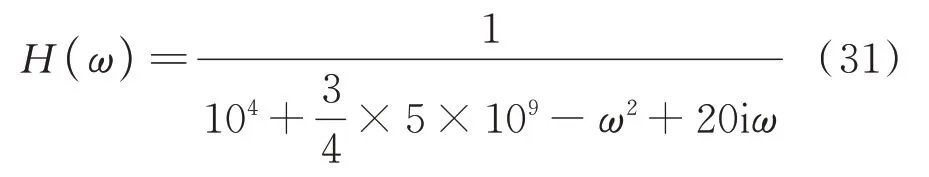
其频率范围与上例一致。将此频响函数运用于复分析Hilbert 变换算法,并进行非线性检测,结果如图4所示,可见其与在线性系统中的使用效果不同,两曲线间差异明显,根据式(29)的准则可判断存在非线性。

图4 Duffing 系统复分析Hilbert 变换非线性检测Fig.4 Nonlinear detection results based on complex analyzed Hilbert transform for the Duffing system
以上两个例子表明,数值积分计算的Hilbert 变换,由于截断误差的存在,使用式(28)的非线性检测准则无法得到可靠结果;而通过复分析理论计算的Hilbert 变换,克服了截断误差且相当精确,因此使用式(29)的非线性检测准则能够给出可靠的结果。
2.3 算例三
进一步考察更复杂的情况。考虑同时存在非线性刚度和非线性阻尼的系统[28]:
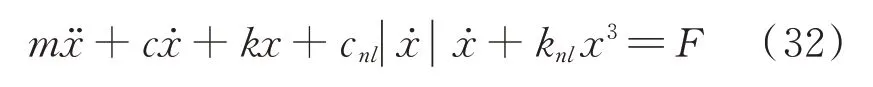
式中m,c和k分别为派生线性系统的质量、阻尼和刚度系数;cnl和knl分别为二次阻尼和三次刚度系数。各参数取值如表1所示。
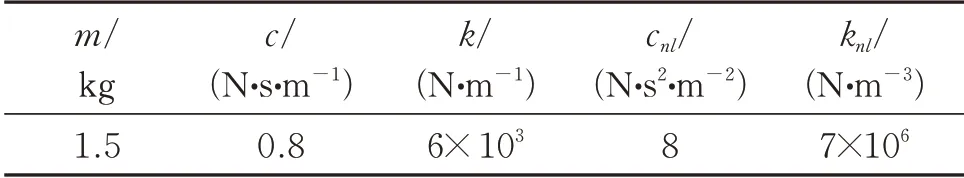
表1 组合非线性系统的系统参数Tab.1 System parameters of combined nonlinear systems
在正弦扫频激励作用下,频响函数复分析Hilbert 变换前后对比如图5所示,两曲线间的差异根据式(29)的准则可判断存在非线性。本例验证了复分析Hilbert 变换非线性检测方法在组合类型非线性系统中的适用性。
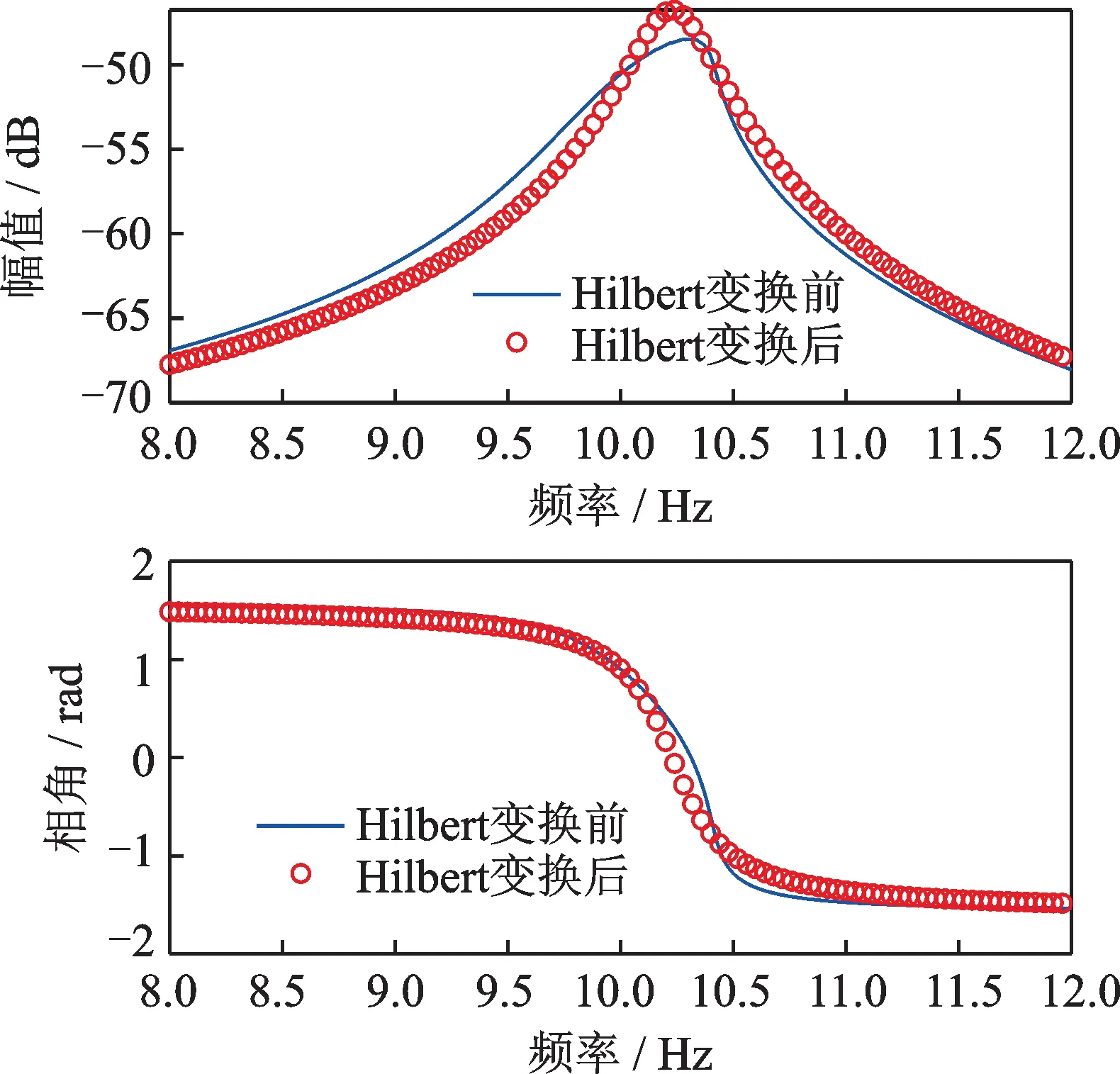
图5 组合非线性系统的复分析Hilbert 非线性检测Fig.5 Nonlinear detection results based on complex analyzed Hilbert transform for the system with combined nonlinear system
2.4 算例四
实际上,上述正弦扫频激励条件得到的非线性频响函数能够产生如“跳跃”现象等较为生动的非线性特征,从而直接实现非线性检测。但是正弦扫频激励不易控制且测试效率较低,因此实际提取频响函数时,随机激励的方式更为常用。下面考虑多自由度非线性系统随机激励下的频响函数。三自由度质量-弹簧非线性系统,其派生线性系统的系统矩阵质量M,刚度K,阻尼C分别为[29]:
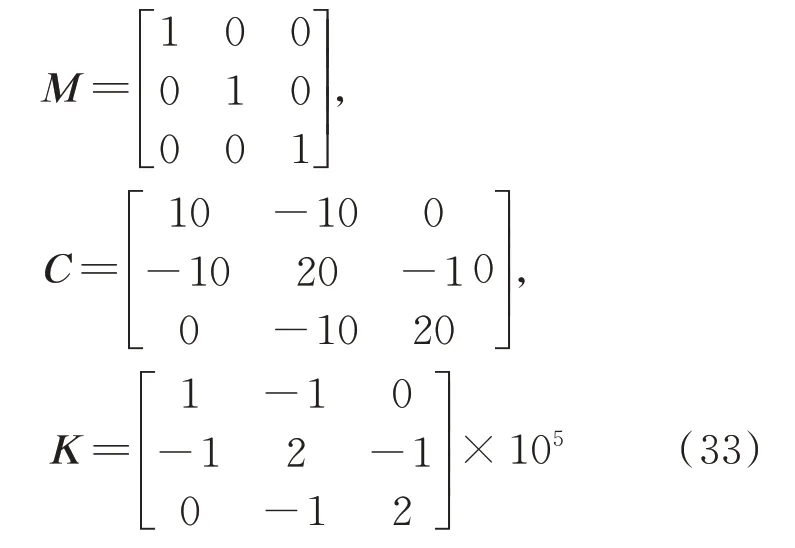
在系统二、三自由度之间存在二次和三次刚度非线性,其非线性恢复力表达为[29]:

式中x2,x3分别表示第二、三自由度的位移。
激励为作用于第一自由度处的高斯随机激励。当随机激励幅值取为500 N 时,频响函数呈现出较为明显的非线性特征。以第二自由度响应的频响函数H21为例,与其派生线性系统相应频响函数的对比如图6所示。此时应用本文定义的非线性检测准则,其效果是可预见的,如图7所示,可根据式(29)判断存在非线性。
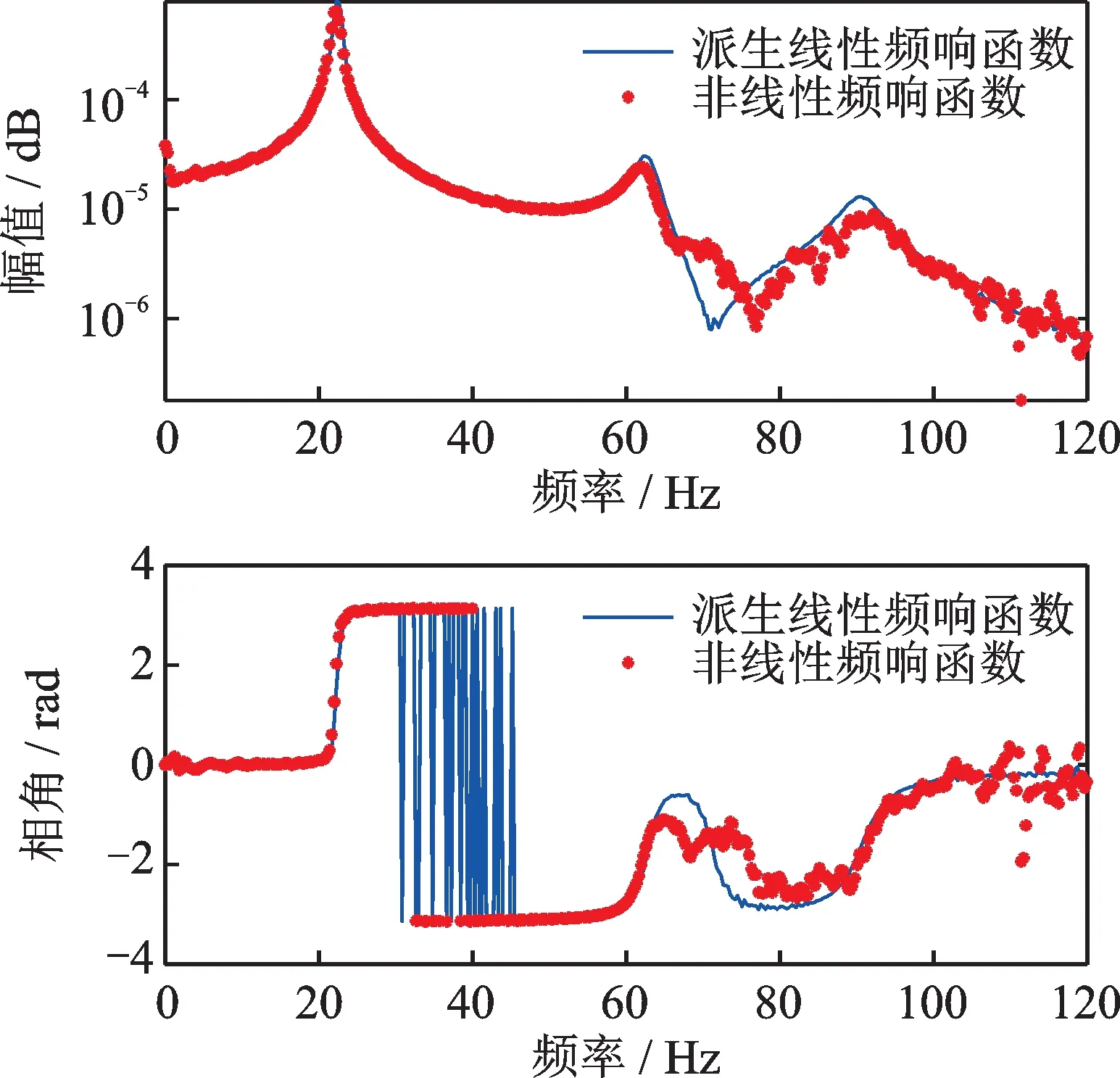
图6 500 N 激励水平的非线性与派生线性频响函数Fig.6 Nonlinear and underlying linear FRF under 500 N level
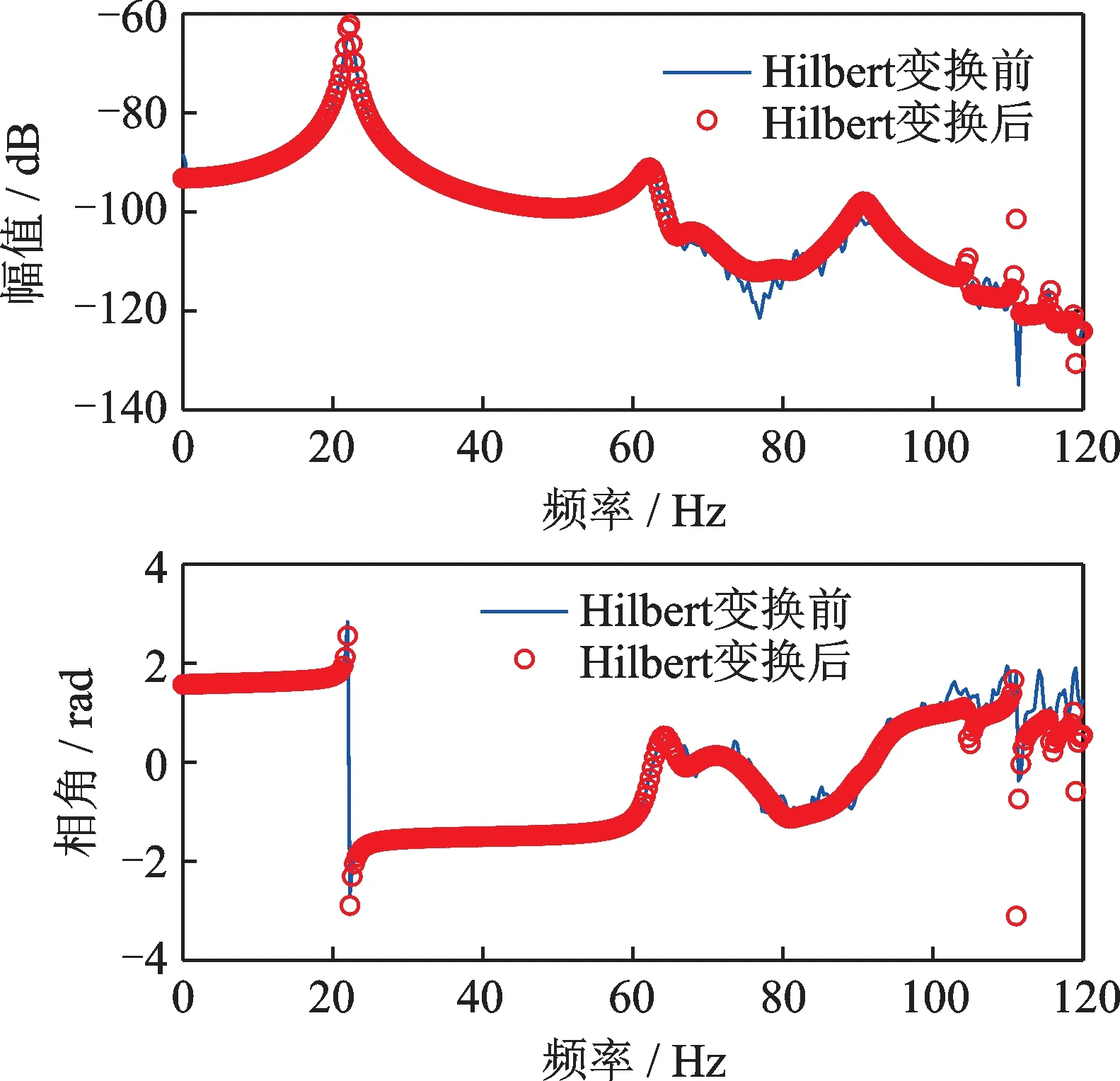
图7 500 N 激励水平复分析Hilbert 变换非线性检测Fig.7 Nonlinear detection results based on complex analyzed Hilbert transform under 500 N level
但当激励幅值较小时,由随机激励得到的频响函数非线性特征将不再明显,此时甚至可近似作为线性情况处理。但是若运用复分析Hilbert 变换非线性检测方法,仍能够检测出非线性的存在。令激励幅值减小为50 N,仍以H21为例,与派生线性频响函数对比如图8所示,可见两者十分接近,仅通过频响函数曲线无法进行可靠的非线性检测。运用复分析理论Hilbert变换进行非线性检测的结果如图9所示,曲线之间显示出的差异可判断存在非线性。因此通过以上多自由度算例可验证,本文定义的Hilbert 变换非线性检测方法不仅能够应用于多自由度非线性系统,而且相比于直接观察频响函数图的畸变,是一种对非线性更敏感的方法,其结果更为准确可靠。

图8 50 N 激励水平非线性与派生线性频响函数Fig.8 Nonlinear and underlying linear FRF under 50 N level
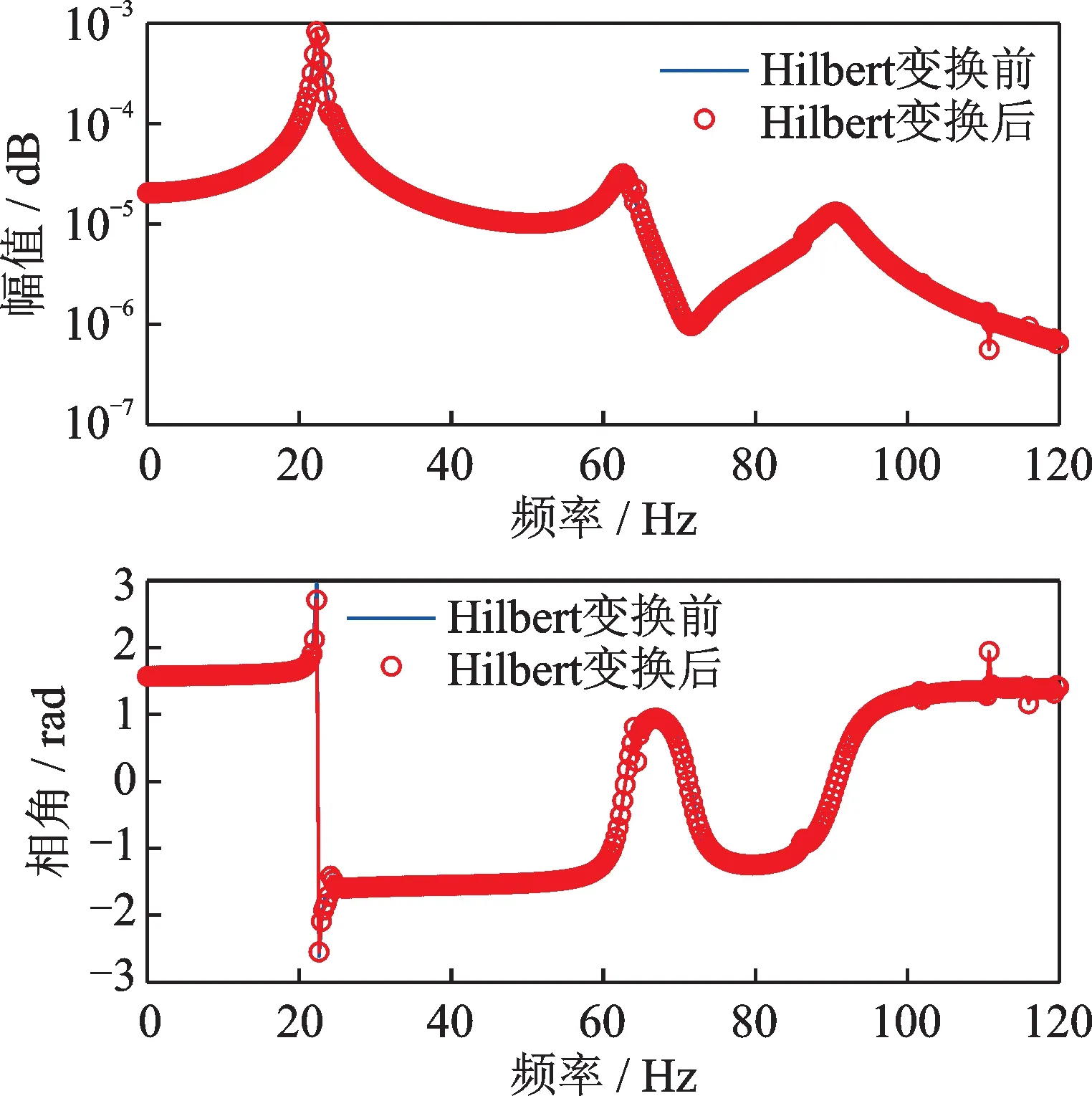
图9 50 N 激励水平复分析Hilbert 变换非线性检测Fig.9 Nonlinear detection results based on complex analyzed Hilbert transform under 50 N level
通过对线性、非线性系统,单、多自由度系统,简谐、随机激励和高、低幅度激励等情况数值算例的综合讨论,验证了基于复分析计算理论的Hilbert 变换算法的准确性,以及复分析Hilbert 变换非线性检测准则的可靠性。Hilbert 变换非线性检测是基于频响函数的方法,因此如果非线性无法反映到频响函数上,则会影响方法检测效果。
3 试验验证
下面通过美国Los Alamos 国家实验室设计的三层剪切型框架结构试验,如图10所示,验证复分析Hilbert 变换非线性检测准则在不连续型非线性刚度结构的应用效果,试验相关细节可参考文献[30]。该试验含有线性和非线性工况,通过二、三层之间的缓冲器引入碰撞非线性,其缝隙可调,对应不同的非线性程度。线性情况对应试验工况1(state 1#),非线性情况本文选取缝隙为0.05 mm 的工况14(state 14#)。

图10 Los Alamos 试验结构示意图[30]Fig.10 Test setup of the experiment of Los Alamos National Laboratory[30]
现考虑激励信号与第三层响应的频响函数。在此试验中20 Hz 以下为结构刚体运动不作为有效的分析数据,取20~100 Hz 频率范围的频响函数,运用复分析Hilbert 变换方法得到线性工况下的非线性检测结果如图11所示,由于两曲线之间十分接近,因此可判断为线性。若使用数值积分计算Hilbert 变换,在此线性工况得到的结果如图12所示,若根据式(28)的非线性检测判据将判断为非线性;可见,数值积分截断误差影响了非线性检测结果,而复分析Hilbert变换计算方法则有效规避了此不利因素。

图11 线性工况复分析Hilbert 变换非线性检测Fig.11 Nonlinear detection results based on complex analyzed Hilbert transform under state 1#

图12 线性工况数值积分Hilbert 变换非线性检测Fig.12 Nonlinear detection results based on numerical integrated Hilbert transform under state 1#
利用复分析Hilbert 对非线性工况进行非线性检测的结果如图13所示。显然,在非线性工况下两曲线之间呈现出明显差异,可根据式(29)判定存在非线性。如不利用非线性检测方法,图13中Hilbert变换前的频响函数曲线实际上与线性工况的形状类似,并未展现出明显的非线性特征,因此无法可靠地判断是否存在非线性。此试验进一步验证了复分析Hilbert 变换的准确性,以及本文定义的Hilbert 变换非线性检测准则的可靠性。实际结构的振动测试可能存在环境噪声、测试设备安装误差、测试设备与被测结构相互作用等诸多因素,使测试结果受到与结构非线性类似的影响,可能造成非线性检测产生误报[13,31]。因此在进行非线性检测之前,需详细检查并确保试验各环节的精细程度,将噪声影响控制在相对较低的水平,这也是进行非线性识别其余环节的先决条件[1,13,31];同时,建议使用多种非线性检测方法相互验证,进一步确保检测结果的可靠性。

图13 非线性工况复分析Hilbert 变换非线性检测Fig.13 Nonlinear detection results based on complex analyzed Hilbert transform under state 14#
4 结 论
Hilbert 变换本身具备坚实的数学理论基础,基于此的非线性检测方法推导过程同样严谨、明确,结果可靠,且对非线性较为敏感,非线性检测性能优异。结合有理逼近理论和复分析理论,Hilbert 变换数值计算的截断误差问题得以解决,扫清了Hilbert变换非线性检测方法迈向实际应用的最后障碍。本文进行了如下创新性研究:
(1)运用留数理论,在Hilbert 变换复分析计算方法的理论推导过程中补充了实轴存在极点的情况,使其更为完善和严谨;
(2)澄清了Hilbert 变换不同定义的使用问题,使Hilbert 变换的复分析计算理论与Hilbert 变换非线性检测理论协调统一;
(3)结合Hilbert 变换复分析计算理论,改进了Hilbert 非线性检测方法的推导格式,建立了新的Hilbert 变换非线性检测准则。
通过数值算例和试验研究验证了复分析Hilbert 变换及其非线性检测准则的有效性和可靠性。但非线性种类繁多难以穷举,此方法尚需不断接受实践检验。也要注意到,本文方法有效的前提是,结构非线性影响能够反映到频响函数上,且其逆Fourier 变换为非因果信号;同时要求测试数据具备较高质量,使得到的频响函数受噪声影响程度弱于结构非线性影响。非线性问题的复杂性决定了,无论是非线性识别中的非线性检测,还是后续的非线性描述、参数识别,找到具有普适意义的方法是一个困难的任务。因此,建议使用多种方法对结果进行交叉验证分析,方可得到可靠结论。但不管结合使用哪些方法进行分析,Hilbert 变换非线性检测方法,以及Hilbert 变换非线性描述、参数识别方法都值得作为其中的一个选择进行实际应用。

