拉杆转子-轴承-密封系统接触刚度矩阵建立及动力学特性分析
武祥林,焦映厚,陈照波
(哈尔滨工业大学机电工程学院机械设计及理论系,黑龙江 哈尔滨 150001)
1 概 述
拉杆转子是一种很常见的转子结构形式,它具有启动快(重量轻),刚性好,以及加工制造方便的优点。经过多年的发展,重型燃气轮机拉杆转子的结构形式已经基本成熟。拉杆转子与传统转子在结构上具有很大的不同,主要表现在转子并非具有传统连续转子的结构形式,而是由一系列轮盘通过拉杆提供的预紧力串联连接组成,轮盘之间存在一些接触平面,如图1所示。实践证明,转子的拉杆以及轮盘间的接触刚度都会对拉杆转子的动力学特性产生重要影响。而由于拉杆及轮盘接触所引起的一些故障也得到了较多研究。
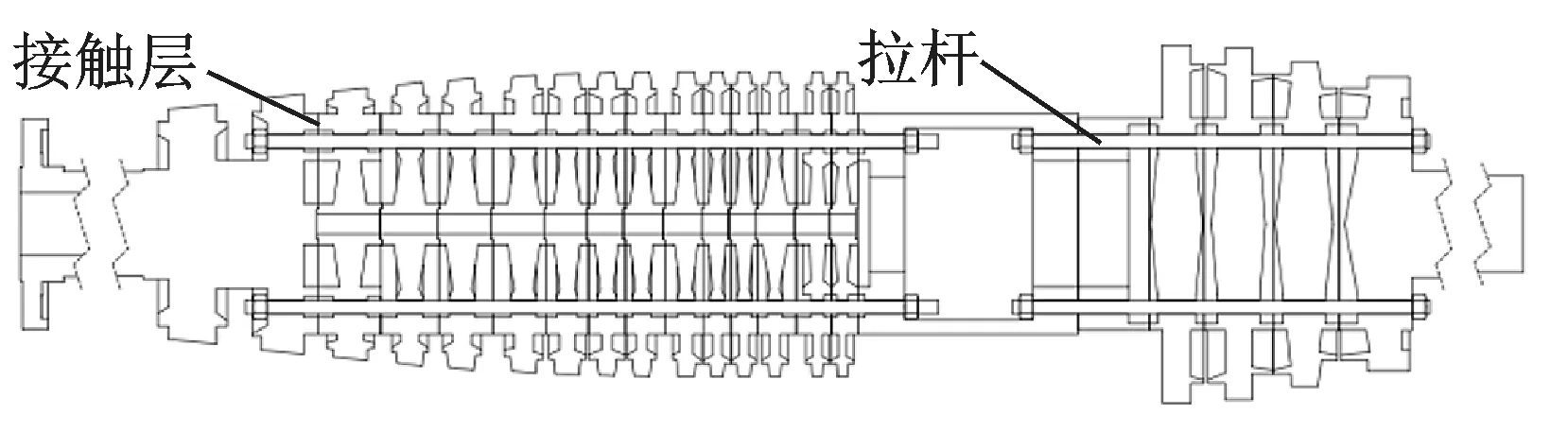
图1 拉杆转子结构示意图Fig.1 Schematic diagram of rod-fastening rotor structure
王荻等[1]报导了由于燃气轮机的启停频繁使转子承受着热应力的循环变化,引起了拉杆的预紧力分布不均,进而导致了燃机转子的振动出现了不稳定的现象。张旋洲[2]报导了由于转子热变形导致的轮盘端面接触不良引起的转子运行初期振动较强的现象。
从这些工程中出现的拉杆转子的故障可以看出,拉杆预紧力以及轮盘端面接触对于转子的动力学特性具有重要影响。因此对于拉杆转子动力学特性的研究具有重要意义。很多学者对含有接触端面的拉杆转子的动力学特性进行了研究工作。
文献[3-4]完善了接触刚度的理论计算方法,并针对周向拉杆转子建立了一种力学模型。计算得到了拉杆转子的固有频率,并与实验测试结果进行了对比,理论计算与实测结果吻合很好。文献[5-7]计算得到了接触界面等效弯曲刚度,但是弯曲刚度并不能表现出接触的全部特点。Hariri等[8]和Nelias 等[9]研究了粗糙表面的接触效应,他们的研究表明接触效应能够明显地减小接触部分的刚度。Isa 等[10]应用一个分段线性刚度模型来表征拉杆Jeffcott 转子接触端面在分离前和分离后的等效弯曲刚度。Zhang 等[11]设计了一个试验用周向拉杆转子,研究表明拉杆转子固有频率随预紧力的增加而提高,逐渐接近整体转子,轮盘表面越光滑,拉杆转子的固有频率越高。Meng 等[12]提出了一种考虑轮盘端面齿接触效应的改进Riccati传递矩阵法,计算得到了等效刚度修正系数,建立了两端轴承支撑的中心拉杆转子动力学模型,计算得到了拉杆转子横向振动的临界转速、振型、不平衡响应等动力学特性。Klmopas[13]和Liu 等[14]的研究都表明预紧力不均会在转子中产生一个附加力矩激励,使转子产生类似初始弯曲的振动特性。
对于转子本身研究的工作虽然重要,但是还不充足,研究考虑油膜力和密封激振力在内的转子系统的动力学行为对于指导工程实际更有意义。
很多学者[15-18]应用Capone 非线性油膜力模型对转子轴承系统的动力学特性进行了分析。目前最著名的密封力模型就是Muszynska[19-20]密封力模型,该模型以一系列实验为基础,具有较高的准确性。以Muszynska 模型为基础,一些学者[21-22]研究了密封对转子动力学特性的影响规律。
本文首先提出一个由七个刚度系数组成的非线性刚度矩阵来表征接触界面。在非线性接触刚度矩阵中考虑了转子变形对刚度系数的影响以及由于接触界面部分分离而引起的接触刚度降低。然后,建立了周向拉杆转子-轴承-密封系统的动力学模型,并使用频谱图分析了其非线性动力学特性。
2 周向拉杆转子⁃轴承⁃密封系统动力学模型的建立
周向拉杆转子的结构示意图如图2所示。该拉杆转子由四个轮盘和多个轴段组成,其中四个轮盘通过12 根拉杆(如图3(a)所示)提供的预紧力连在一起,每两个轮盘之间连接部分为接触端面,是一个圆形平面。转子的两端由两个滑动轴承支撑。当采用有限元法对该拉杆转子进行建模时,需要对拉杆、接触层、轮盘以及转子轴段分别进行建模。下面介绍各个部分的建模过程。

图2 周向拉杆转子结构示意图Fig.2 Schematic diagram of circumferential rod-fastening rotor structure
2.1 对周向拉杆的建模
沿周向均匀分布的拉杆如图3(a)所示。由于拉杆较细、质量较轻,所以在对拉杆进行动力学建模的时候忽略了拉杆的质量以及结构阻尼,只考虑拉杆的刚度,将拉杆等效为一个沿轴向伸缩变形的弹簧[14]。

图3 拉杆变形以及位置分布示意图Fig.3 Schematic diagrams of deformation and position distribution of rod-fastening
如图3(b)所示,将拉杆两端所在轮盘a 和轮盘d端面的转角位移表示为(αaβaαdβd)T,得到拉杆所提供的轴向力可以表示为:
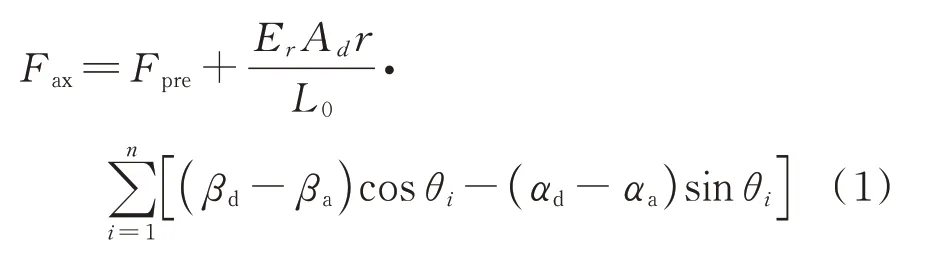
拉杆所引入的刚度矩阵以及广义力矩可以分别表示为:

其中

式中Ω表示转子的转速。
2.2 对接触层的建模
Greenwood 等[23]曾经引入了GW 模型研究含有高斯分布的微凸体的粗糙平面与水平刚性平面的接触,由该模型可以得到单位面积接触平面的压力、垂直接触刚度、剪切刚度为:

式中p为接触面垂直压强;kn为单位面积上的垂直接触刚度;kτ为单位面积上的切向刚度;Ds为单位名义接触面积上微凸体的个数;Rs为微凸体的曲率半径;σ为粗糙表面高度的标准差;s表示粗糙平面标准化微凸体高度;E′为等效杨氏模量,E′=,其中,ν表示泊松比,下标1和2 针对的是形成接触对的粗糙表面1 和2;h为标准化接触间隙,h=d0/σ,其中,d0为两个接触面的平均接触间隙,即接触层的初始厚度;ϕ(s)为标准化峰值高度分布函数,ϕ(s)=
公式(4)表明单位面积的垂直接触刚度是接触压强的隐函数,他们的关系可以通过数值方法求得。
研究一个具有圆形接触端面(如图4所示)的接触层,该接触层的初始厚度为d0,并且该接触层可以分为接触区域和分离区域两部分,两部分的边界为一条直线,叫做分离线,如图4和5 所示。
为了计算接触层的接触刚度,需要先建立三个坐标系,如图4所示。第一个坐标系为x*y*z*,该坐标系的x*轴平行于分离线,y*轴的正向指向接触区域压强增加的方向,z*轴垂直于变形前的接触面。第二个坐标系为全局坐标系xyz,该全局坐标系由坐标系x*y*z*绕z*轴旋转角度β得到。如果将全局坐标系xyz先沿着x轴平移位移xˉ,再沿y轴平移位移就可以得到第三个坐标系x′y′z′,其中是接触区域在坐标平面xoy中的形心。

图4 接触端面示意图Fig.4 Schematic diagram of contact interface
首先,假设接触平面上的压强p为坐标x和y的线性函数[6]:
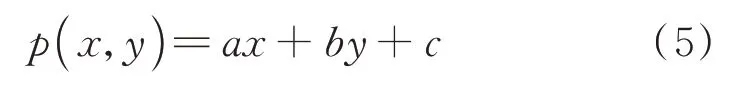
式中a,b和c为待定系数。
轴向压力P,接触层两端弯矩M可以在坐标系xyz中表示为:

式中A为名义接触面积;Sy为接触面对x轴的静矩;Sx为接触面对y轴的静矩;Ix为接触面对y轴的惯性矩;Iy为接触面对x轴的惯性矩;Ixy为接触面的惯性积。它们的取值可以表示为:
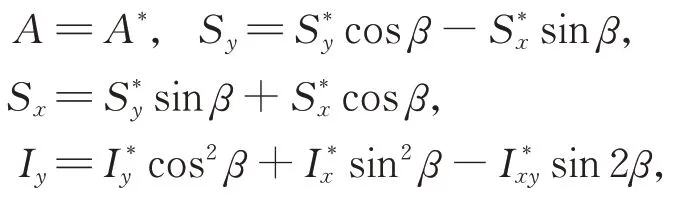

式中S*y表示接触端面对x*轴的静矩;S*x为接触端面对y*轴的静矩;I*y为接触端面对x*轴的惯性矩;I*x为接触端面对y*轴的惯性矩;I*xy为接触端面的惯性积。它们的值可以通过如下公式求得:

其中,上述公式中的τ=y/R,τ0为:

式中τ1=的物理意义是分离线距离接触端面圆心的无量纲距离。
τ1是判断接触层接触状态的重要参数,当分离线距离接触端面圆心的无量纲距离大于1,且接触端面处于分离区域一侧时,有τ1≤−1,此时接触层两接触面处于完全分离的状态,这种状态只是一种极限情况,它表示本来接触的两轮盘已经完全脱离,这种状态在实际情况中并不会发生;当分离线距离接触端面圆心的无量纲距离大于1,且接触端面处于接触区域一侧时,有τ1≥1,此时接触层处于完全接触状态,当−1<τ1<1 时,表示分离线距离接触端面圆心的无量纲距离小于1,接触层处于部分接触状态,这种状况经常发生在当转子预紧力不足或者预紧力不均匀的情况下。上述参数求出之后,就可以求出a,b和c:

其中:

并且接触面的压力P以及弯矩Mx和My可以通过拉杆两端所在的轮盘端面的转角位移的差值和接触层两端面的转角位移的差值表示出来,如下式所示:

式中Eeq为接触层等效的弹性模量;αj−αj+1表示接触层两个端面绕x轴的转角位移的差值;βj+1−βj表示接触层两个端面绕y轴的转角位移的差值(如图5所示);j和j+ 1 表示接触层两端的节点编号。

图5 接触层微观变形示意图Fig.5 Schematic diagram of microscopic deformation of contact layer
由公式(6)和(11)可以看出,接触端面上一点的压强不仅与该点所在的位置有关,还由接触层两个接触端面的转角位移差以及拉杆提供的预紧力决定。而接触端面上一点的压强又决定该点的垂直接触刚度以及切向刚度。因此,通过上述关系就可以建立接触刚度与接触层两端面位移之间的联系。
可以在坐标系x′y′z′中得到接触端面上一点的压强p(x′,y′)与该点的垂直接触刚度kn的关系:

剪切刚度与垂直接触刚度的关系如式(4)所示。
已知单位面积上的垂直接触刚度以及剪切刚度后,可以求出接触刚度所引入的弹性势能,对于一个微元接触平面,弹性势能可以表示为:

将式(14)向坐标系x′y′z′进行坐标变换,并在整个接触平面上进行积分:

式中qc=(xj,yj,αj,βj,γj,xj+1,yj+1,αj+1,βj+1,γj+1)T为接触层两接触端面节点的位移向量;xj,j+1,yj,j+1表示的是全局坐标系中两接触端面节点在转子x,y轴方向的位移,αj,j+1,βj,j+1,γj,j+1表示的是两接触端面分别绕全局坐标系x,y,z轴的转角;A′表示的是坐标系x′y′z′中的面积微元;Kc为接触刚度矩阵,该矩阵中的元素可以表示为:

其中:

在此需要说明,用上述方法所建立的接触刚度矩阵为非线性接触刚度矩阵,该刚度矩阵可以考虑接触层微变形所引起的刚度系数的变化,也可以考虑拉杆轴向力的变化而引起的刚度系数的变化,如果忽略上述两个因素,该接触刚度矩阵可以退化为线性接触刚度矩阵。
2.3 转子⁃轴承⁃密封系统动力学模型的建立
除了上述建模,采用刚性轮盘以及每个节点具有五个自由度的Timoshenko 梁模型[24]对拉杆转子的轮盘和轴段进行建模,同时考虑上述所建立的拉杆动力学模型、非线性接触刚度矩阵、非线性油膜力模型和密封力模型,最后拉杆转子-轴承-密封系统的动力学模型可以表示为:
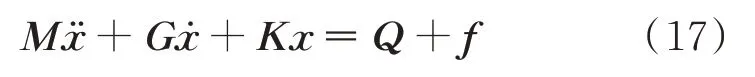
其中:
M=Ms+Md,G=Gs+Gd+Cs,
K=Ks+Krod+Kc,Q=Qd,
f=frod+foil+fseal。
式中M,G和K分别代表质量,陀螺和刚度矩阵;Q表示不平衡激励力;f表示拉杆引入的广义力矩、油膜力和密封激振力的向量和;上标s 和d 分别代表转子轴段和轮盘;对于n个节点,x=[x1,y1,α1,β1,γ1,…,xn,yn,αn,βn,γn]T表示位移向量。
质量矩阵和陀螺仪矩阵的组装与传统方法相同,但是刚度矩阵的组装在这里有所不同,因为接触层和拉杆引入的刚度矩阵将在组装后改变刚度矩阵的结构。刚度矩阵的组装规则如图6所示。

图6 刚度矩阵的组装规则示意图Fig.6 Schematic diagram of the assembly rules of the stiffness matrix
需要说明的是,在陀螺矩阵中考虑了转子的结构阻尼,而在工程实际中,结构的阻尼通常假设为瑞利阻尼,也就是说阻尼矩阵可以表示为质量矩阵和刚度矩阵的线性组合,这种能量耗散的模拟方法在数值分析中具有很大的优势,能够满足一般结构动力分析的需求。在本文中,采用瑞利阻尼表示转子的结构阻尼,该阻尼可以通过如下公式表示:

式中ωn1和ωn2分别为第一阶和第二阶固有频率,单位为r/min;ξ1和ξ2分别为第一阶和第二阶模态阻尼比。在本研究中,取ξ1=0.02 和ξ2=0.04。
除此之外,foil表示的是油膜力向量,在这里采用了一种基于短轴承理论的非线性油膜力模型[20],该模型已经通过实验验证具有良好的精度,并且该模型也具有较高的计算效率:

式中μb表示润滑油黏度;Rb,Lb和hb分别表示轴承半径、轴承宽度和径向间隙。在本研究中上述参数取值为:μb=0.04 Pa·s,Rb=0.04 m,Lb=0.04 m,hb=2×10−3m。无量纲油膜力fbx,fby表示如下:
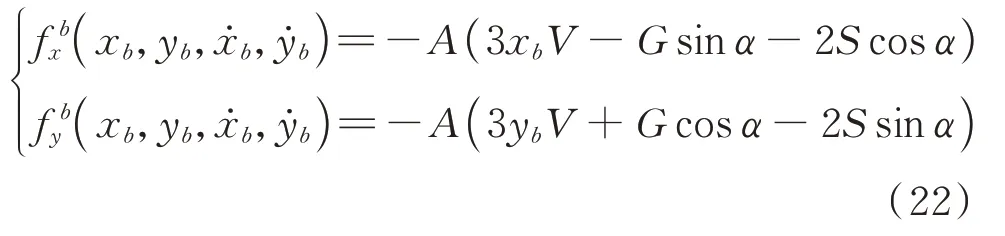
上述公式中的函数A,V,S,G,和α在文献[22]中有详细描述,这里不再赘述。另外,fseal表示密封激励力向量。在这里采用Muszynska 模型来描述非线性密封力,它不仅反映了密封力的非线性特征,而且明确描述了密封力的物理含义。
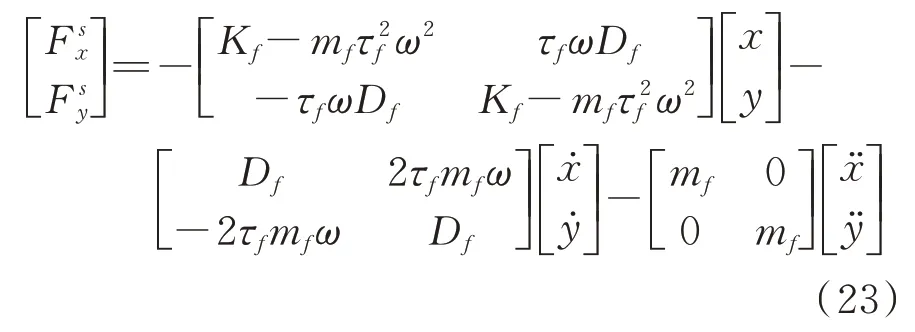
式中Kf,mf,Df和τf分别表示当量刚度、当量质量、当量阻尼和流体周向速度比。这些参数都是转子位移的非线性函数,即:

式中e=为转子相对偏心位移,其中,Cr为密封间隙;n,b和τ0均为与迷宫密封结构相关的经验系数,一般τ0<1/2。Kf,Df以及mf可以用Childs 提出的动力学计算公式计算得出:
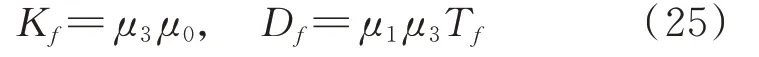
其中:

式中σf为摩擦损失梯度系数;ξ为密封介质周向进口损失系数;lf为密封腔体宽度;v为当量轴向速度;Rf为密封半径;ΔP为气体通过密封后的当量压降;m0和n0为Hirs 湍流方程的系数;Ra和Rv分别为轴向和周向Reynolds 数;υ为气体动态黏度系数。上述密封参数分别取值为:Cr=1×10−3m,ξ=0.1,lf=0.04 m,v=10,Rf=8.1×10−3m,ΔP=1×106Pa,m0=0.25,n0=0.079,υ=1.5×10−5。
为了求解方便,引入了无量纲因子δ,将动力学方程进行无量纲处理:

将上述公式代入到动力学方程中,得到无量纲化的动力学方程为:

公式(27)可以通过数值方法求解。本文采用Newmark-β积分方法求解是因为它是一种在时域内求解非线性方程的鲁棒算法。这里在求解动力学方程(28)的每个子步骤中都需要判断接触层的接触状态,然后根据判断出的接触状态,决定使用相应的策略计算接触刚度矩阵Kc。当完成所有计算步骤或接触层完全分离时,终止计算过程,计算流程如图7所示。

图7 计算流程图Fig.7 Schematic diagram of the calculation process
3 计算结果及分析
在前面的研究中,首先对周向拉杆转子的拉杆以及接触端面进行了建模,在此基础上继续建立拉杆转子-轴承-密封系统的动力学模型,并分析一些结构参数对该系统动力学特性的影响规律。除了上述已经给出的密封和轴承参数外,其余结构参数如表1所示。

表1 拉杆转子结构参数Tab.1 Structure parameters of the rod⁃fastening rotor
计算得到预紧力为1.2 kN 时,拉杆转子的一阶临界转速为4558.3 r/min,二阶临界转速为10425 r/min;预紧力为4.8 kN 时,拉杆转子的一阶临界转速为5050.7 r/min,二阶临界转速为10618 r/min,连续转子的一阶临界转速为5320.8 r/min,二阶临界转速为10678 r/min。
如图8所示,将拉杆转子离散为具有14 个Timoshenko 梁单元、18 个节点、四个刚性轮盘的有限元模型。周向分布拉杆的两端点分布在节点5 和14。在节点(6,7),(9,10)和(12,13)之间形成三个接触界面。为了进行比较分析,同样建立了具有四个刚性轮盘的连续转子-轴承-密封系统的有限元模型,该模型具有11 个单元和12 个节点。除拉杆和接触界面外,该转子与拉杆转子结构相同。两个转子的不平衡力都来自四个轮盘的质量偏心,设定为ea=eb=ec=ed=e=1×10−4m。

图8 两种转子-轴承-密封系统有限元模型Fig.8 Finite element model of two kinds of rotor-bearing-seal system
3.1 预紧力的影响
首先分析了拉杆预紧力对拉杆转子-轴承-密封系统动力特性的影响规律。提取了连续转子-轴承-密封系统和具有12 根拉杆且预紧力均匀分布的拉杆转子-轴承-密封系统中左轴承处节点x方向的频谱图,如图9所示,图中X表示无量纲频谱幅值。
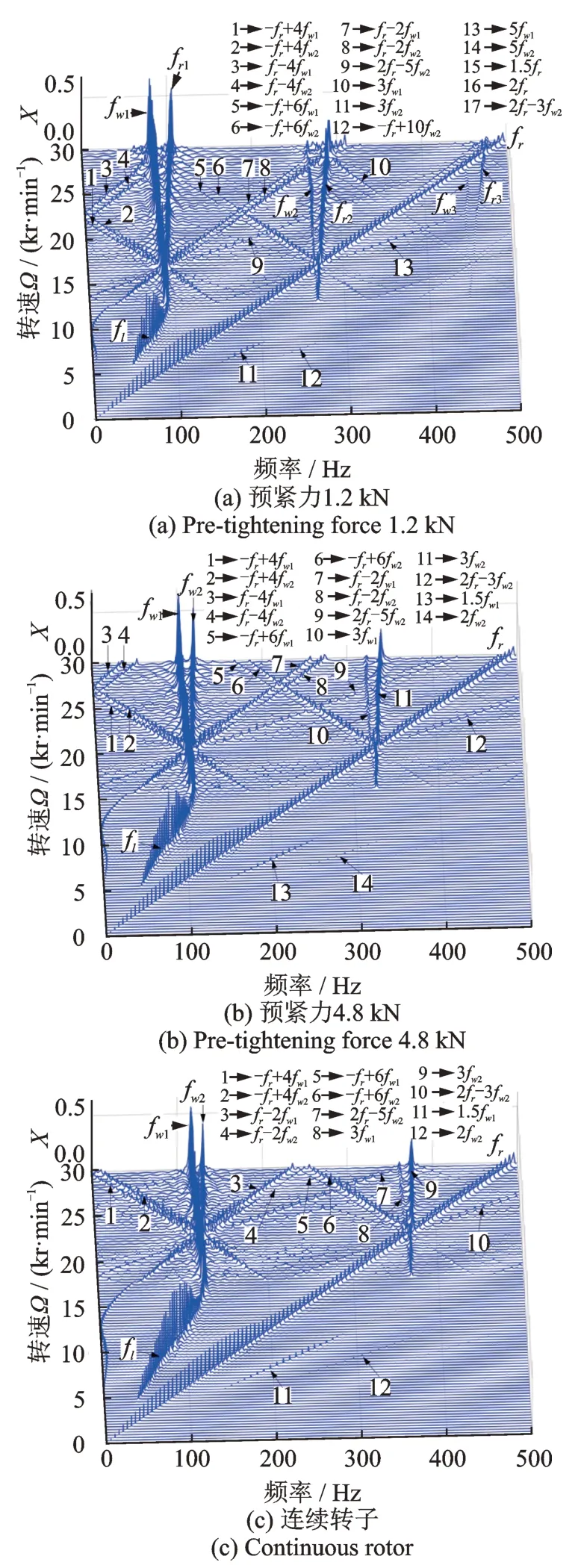
图9 转子-轴承-密封系统频谱图Fig.9 Spectrum diagram of rotor-bearing-seal system
在图9(a),(b)中,总预紧力分别为1.2 kN 和4.8 kN。由图9(a)可以看出,在低速范围内运行时(Ω≤6000 r/min),拉杆转子-轴承-密封系统的振动主要由转子的不平衡量引起的,频谱图中仅存在单一的工频成分fr。随着转子转速的升高,当转子的转速为Ω=6000 r/min 的时候,0.5 倍工频分量、1.5倍工频分量和2 倍工频分量同时出现;当转子转速为Ω=12600 r/min 的时候,0.5 倍工频分量消失,并且在此区间(Ω∈[6000 12600]r/min),0.5 倍工频占主导地位,此时可以知道,系统出现了油膜涡动。当转子转速Ω∈[6000 8400]r/min 时,系统同时存在四种频率成分的。随着转速的继续增加,当转速Ω≥12600 r/min 时,除了工频外,系统还出现了油膜失稳频率fw2和气膜失稳频率fw1,以及与它们相关的组合频率。此时系统的自激频率成分(fw)、系统工频(fr)以及他们的组合频率同时存在,且自激频率成分占主导地位,而组合频率成分表明了油膜力与密封力的耦合作用。
对比图9(a)~(c)可以发现,预紧力对拉杆转子-轴承-密封系统的动力学特性影响很大,同时拉杆转子与连续转子的动力学特性有很大区别。如图9(a),(b)所示,随着预紧力由1.2 kN 增加到4.8 kN,拉杆转子-轴承-密封系统中0.5 倍工频(0.5fr)出现的转速下限值由6000 r/min 降低为5400 r/min,并逐渐逼近连续转子0.5 倍工频(0.5fr)出现的转速下限值4800 r/min;同样随着预紧力的增大,拉杆转子0.5 倍工频消失的转速上限值由12600 r/min 增大为15600 r/min,也逐渐逼近连续转子0.5 倍工频(0.5fr)消失的转速上限值17700 r/min。除此之外,预紧力的增加同样改变了组合频率出现与消失的阈值。例如,随着预紧力的增加,拉杆转子-轴承-密封系统1.5倍工频(1.5fr)出现的范围会变大,同样逐渐逼近连续转子-轴承-密封系统的频率范围。在Ω∈[0 30000]r/min 转速范围内,随着拉杆转子预紧力的增加,有些组合频率成分已经不在显示的范围内。例如,随着预紧力的增加,组合频率成分5fw1和5fw2消失在了该范围内。上述现象表明,预紧力会影响激振频率与组合频率出现与消失的阈值,随着预紧力的继续增加,拉杆转子-轴承-密封系统的动力学特性逐渐接近连续转子-轴承-密封系统的动力学特性。
这里还可以发现,连续转子出现油膜涡动(0.5fr)的转速是低于拉杆转子出现油膜涡动的转速的,而油膜涡动是引起转子系统失稳的一个重要原因,因此可以认为,在结构参数相同时,拉杆转子-轴承-密封系统的稳定性是高于连续转子-轴承-密封系统的。同样,由于0.5 倍工频(0.5fr)消失的转速上限值等于转子出现自激振荡频率(fw)的阈值,因此预紧力的增加提高了转子出现自激振荡频率(fw)的阈值。
3.2 预紧力不均的影响
预紧力不均对拉杆转子-轴承-密封系统的动力学特性的影响规律如图10所示。将相对位置不同的两个故障拉杆的预紧力以及其弹性模量设置为0,目的是为了模拟转子部分拉杆出现断裂导致预紧力出现不均的情况,同时也研究故障拉杆的相对位置对转子-轴承-密封系统的动力学特性的影响规律。对比图10与图9(b),可以发现预紧力不均对于拉杆转子-轴承-密封系统的动力学特性具有重要影响。

图10 不均匀预紧力下,拉杆转子-轴承-密封系统频谱图Fig.10 Spectrum cascades of the rod-fastening rotor-bearingseal system under unevenly distributed preload
首先预紧力不均会导致系统出现新的频率成分,例如fw3和fw4及其组合频率成分,并且故障拉杆的相对位置会对于系统的组合频率成分产生重要影响。当两故障拉杆的位置相邻时(如图10(c)所示),自激振荡频率fw3和fw4并不明显,同时系统存在组合频率成分3fw4,但不存在组合频率成分3fw3;随着两故障拉杆由邻位(如图10(c)所示)向对位(如图10(a)所示)变化,自激振荡频率fw3和fw4逐渐变得明显,组合频率成分3fw3也从无到有,逐步变得明显。由此可以通过频率成分的变化来判断故障拉杆的相对位置,这对于拉杆转子-轴承-密封系统的健康监测以及故障诊断有理论指导意义。除此之外,接近邻位的故障拉杆更明显地降低了系统的稳定性,当两故障拉杆处于对位时(如图10(a)所示),系统在转子转速为Ω=5700 r/min 时出现了涡动频率fl;当两故障拉杆接近邻位时(如图10(c)所示),系统在转子转速为Ω=3000 r/min 时出现了涡动频率fl。因此可以得出结论,随着两故障拉杆由对位向邻位变化,系统的稳定性降低。产生这种现象的原因是,随着两故障拉杆由对位逐渐变为邻位,拉杆所产生的不平衡弯矩会变大,同时预紧力不均导致的接触层在两垂直方向上的弯曲刚度的差异也变大,这导致了系统的稳定性明显降低。
4 结 论
本文首先建立了表征轮盘之间的接触效应的非线性接触刚度矩阵,在非线性接触刚度矩阵中考虑了转子变形对刚度系数的影响以及由于接触界面局部区域的分离而引起的接触刚度降低。其次建立了周向拉杆转子-轴承-密封系统的动力学模型。最后用频谱图分析了不同预紧力和不均匀预紧力对拉杆转子-轴承-密封系统的非线性动力学特性的影响规律。得出结论如下:
(1)随着预紧力的增加,拉杆转子-轴承-密封系统的动力学特性逐渐接近连续转子-轴承-密封系统的动力学特性。相同结构参数下,拉杆转子-轴承-密封系统具有更高的稳定性。
(2)预紧力不均降低了拉杆转子-轴承-密封系统的稳定性。当两故障拉杆处于邻位时,拉杆转子-轴承-密封系统稳定性急剧降低。
(3)预紧力不均会导致系统出现新的自激振荡频率成分,并且故障拉杆的相对位置对于系统的组合频率成分也会有重要影响。随着两故障拉杆的相对位置由邻位到对位变化,自激振荡频率fw3和fw4逐渐变得明显,组合频率成分3fw3也从无到有并且逐步变得明显。由此可以通过自激振荡频率及其组合频率成分的变化来诊断故障拉杆的相对位置。

