异宿轨道破缺诱发的非轨道面绳系卫星混沌运动

余本嵩，汤毓宁

（南京航空航天大学机械结构力学及控制国家重点实验室，江苏 南京 210016）

引 言

空间绳系系统以其低能耗、可重构、易循环使用等优势已成为当今航天领域探索的热门课题之一，其在碎片捕获、返回舱再入、废弃物离轨、对地侦查、星际探测等诸多方面的不断发展，更是使国内外广大学者在其理论、实验、应用等方向投入大量精力［1-7］。

非轨道面绳系系统动力学研究是其由理论到实际应用的重要环节，已有相关科研成果呈现。比如，对于面内外运动耦合的空间电动力绳，Kojima 等［8］为了维持系统在倾斜轨道下的稳态运动，设计了一套时滞反馈控制律，实现了对不规则振荡的有效抑制。Ellis 等［9］理论分析自旋绳系卫星时发现，微幅面外振动不会对系统面内运动产生影响，且相对高速的面内自旋会使面外运动更加稳定。Avanzini等［10］对非轨道面、双金字塔型等绳系编队进行数值研究，算例表明系统稳定性对系绳线密度、阻尼、刚度等参数较为敏感。杨育伟等［11］利用摄动法解析得到面外电动力绳系卫星的近似周期解，并通过Poincaré 映射判定该周期运动的稳定性。Paul 等［12］基于反馈线性化方法尝试对绳系卫星系统面内/面外振荡进行控制，面内振荡得到有效抑制，面外振动控制效果不理想。Yoon 等［13］通过等效缩比地面实验，研究空间系绳面外圆周运动，对系统振动频率等进行讨论，实验与有限元计算结果一致。在空间碎片移除应用背景下，Cui 等［14］充分分析系绳缠绕等不稳定因素，计算出初始面内/面外倾角的合理范围，以保证电动力绳安全释放。

对于包括混沌在内的空间系绳非线性特性研究，仍主要聚焦于系统面内运动。譬如，Nakanishi等［15］基于哑铃模型研究轨道平面内两体绳系卫星，数值结果表明，当轨道偏心率大于0.3138 时系统面内俯仰运动会出现混沌现象，并通过将不同轨道下面内运动轨迹投影于van der Pol 平面以展示系统概周期、混沌特性。考虑主航天器刚体姿态，庞兆君等［16］开展绳系航天器动力学地面等效实验，依据天-地动力学相似原理，揭示在轨刚体混沌运动，同时提出通过阻尼力矩对混沌进行抑制。采用离散珠点模型，并计入热冲击、大气阻尼等环境摄动，Yu 等［17］讨论了由轨道偏心率变化引起的绳系卫星面内俯仰运动分岔行为。Malashin 等［18］用非线性偏微分方程构建空间绳系系统模型，并基于该模型提出边界控制问题，从而解析分析柔性系绳的横向/纵向非线性振荡及抑制方法。Lim 等［19］采用绝对节点坐标法数值研究空间绳-网系统对轨道碎片的捕获过程，提出大量关于柔性系绳缠绕、冲击等非线性问题。Aslanov等［20］分析一类面内绳系拖曳系统，仿真结果显示，随着系绳长度增加，面内俯仰角及刚体姿态角的平衡位置皆会发生超临界叉型分岔。Liu 等［21］探讨在地-月引力场作用下含阻尼绳系系统的三体问题，算例展示系统在L1和L2点附近存在概周期及混沌等运动。针对电动力绳系航天器升轨技术，Li 等［22］通过模拟发现，无控状态下系绳长度、系统面内外运动皆为非周期振荡。Salazar 等［23］以数值方式呈现状态保持阶段面内外耦合（即四维状态空间）绳系卫星的混沌运动，并基于Kelvin-Talt-Chetayev 定理设计拉力控制器对混沌进行抑制。

可以看出，非轨道面绳系卫星的周期运动稳定性及控制方法得到了大量关注，但对其混沌动力学却鲜有涉及，而对面内系统的混沌特性也多局限于数值讨论，理论研究不充分。本文致力于面外绳系系统的混沌运动预测分析，具体讨论面内俯仰角保持恒定仅做面外滚转的绳系卫星，揭示面外摄动引起的混沌，并给出混沌发生的必要条件，最后通过数值仿真进行验证。

1 非轨道面滚转绳系卫星模型

由主星M、子星S 及起连接作用的绝热系绳构成的在轨绳系卫星系统，如图1所示。主星与子星皆为圆柱体，质量分别为mM和mS。考虑到状态保持阶段系绳始终处于紧绷状态，故将其简化为线密度为ρt、长度为l、直径为dt的刚性杆，其两端延长线与卫星圆柱体轴线重合。假设地球为均质球体，系统质心o位于距地高度为Ho的绕地圆周轨道，在轨道平面Π 和非轨道平面Σ，系统运动可分别以面内俯仰角θ和面外滚转角ϕ表示。为讨论非轨道平面系统滚转运动，施加与非轨道平面Σ 正交的控制力，使系统保持恒定的面内俯仰角θC。此外，以ν表示绕地真近点角，以i表示轨道与赤道平面夹角。构建固结于系统质心o的轨道坐标系o-xyz，其x轴指向系统运动方向，y轴正交于轨道平面，z轴指向地球质心。

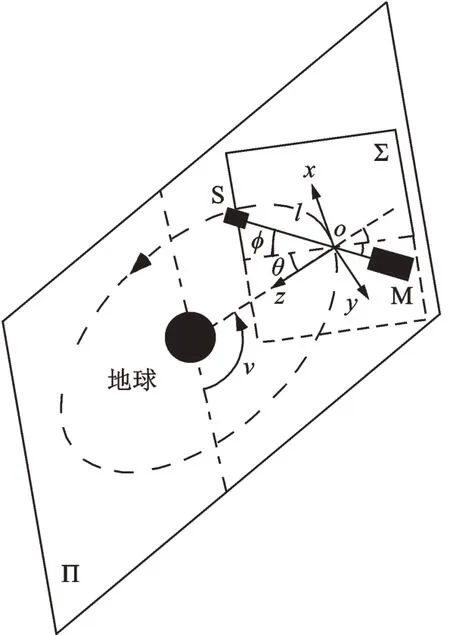
图1 面外滚转绳系卫星系统Fig.1 Tethered satellite system with out-of-plane roll motion

基于第二类Lagrange 方程建立系统动力学模型。首先，系统质心绕地和其自身滚转而产生的动能可分别表示为：

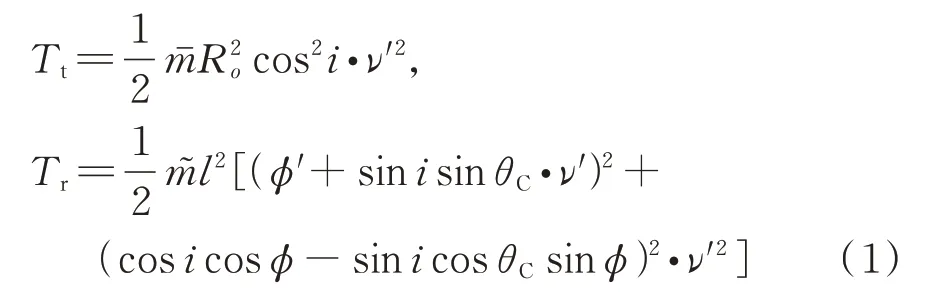
式中 符号“′”表示变量对时间t求导，Ro表示系统质心距地球质心的位置标量，=mM+mS+mt和为导出质量参数，mt=ρtl为系绳质量。同时，以无穷远处为势能零点，列出系统势能：

式中μE表示地球引力参数。

选取面外滚转角ϕ为广义坐标，将系统动能T=Tt+Tr及以上势能表达式代入第二类拉氏方程可得［24］：

式中Qϕ表示与广义坐标ϕ对应的广义力。另外，图1所示的真近点角ν，其相比于时间t能够更直观地展示系统轨道历程，故以真近点角ν作为无量纲时间，用Lr表示参考长度，引入无量纲变换：

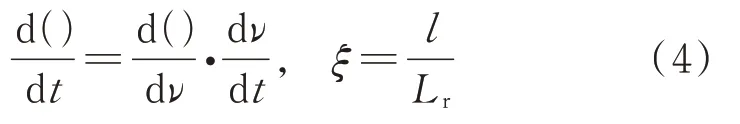
则系统动力学方程（3）可转化为以下无量纲形式：

式中 符号“⋅”表示变量对无量纲时间ν求导。以上动力学模型能够对具有恒定面内俯仰角的绳系卫星滚转运动进行描述。

2 摄动激励

考察大气阻尼及太阳光压对系统面外滚转的摄动作用，基于虚功原理和力矩表达式可得到它们引起的摄动力矩，即与面外滚转角对应的广义力［25］：

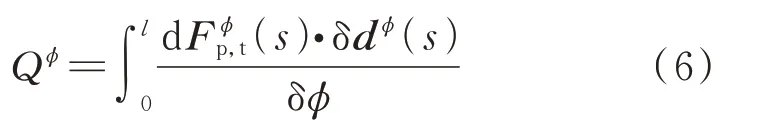
式中 dFϕp，t(s)为作用于系绳微元段ds的面外摄动力，而由虚面外滚转角δϕ引起的微元段ds的虚位移表示为：

式中 ex，ey和ez分别表示与坐标轴x，y和z对应的单位矢量；s表示一个度量由子星指向主星的局部长度坐标，χ=(2mM+mt) (2mˉ)为导出参数。

作用于卫星刚体和系绳微元段ds的大气阻尼力为：

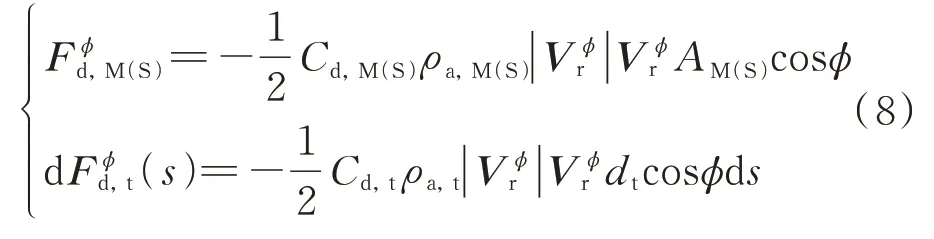
式中Cd，M(S)和Cd，t表示卫星刚体和系绳的大气阻尼系数，ρa，M(S)和ρa，t表示卫星刚体和系绳所处轨道高度的大气密度，Vϕr表示系统在面外方向相对于大气的速度矢量，AM(S)表示卫星刚体的迎风面积。将卫星刚体承受的大气阻尼力对系统质心取矩，而将式（8）中的第2 式代入式（6），得到大气阻尼在广义坐标ϕ方向作用于主卫星刚体、子卫星刚体及系绳的摄动力矩：

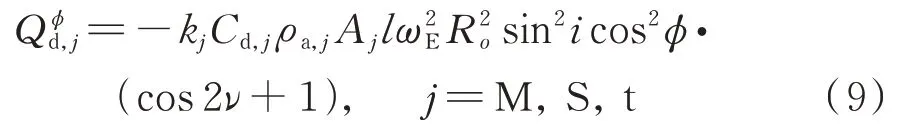
式中ωE为地球自旋角速度。

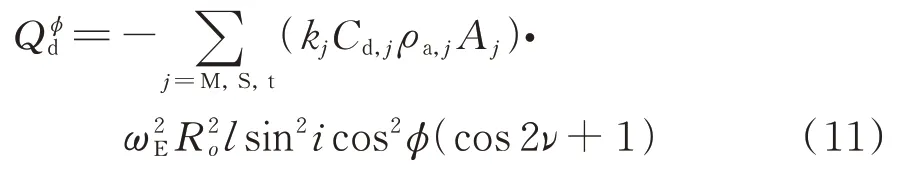
系统处于始终向阳的绕地轨道，则作用在卫星刚体和系绳微元段ds的太阳光压力表示为：

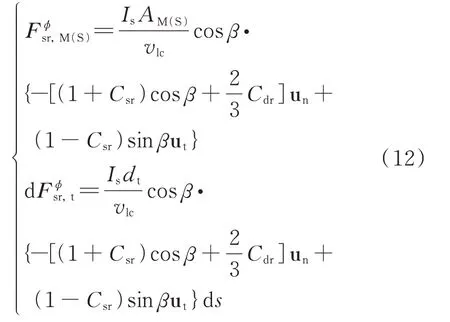
式中Is=1372 W ⋅m−2表示太阳在地球表面的入射辐射能流密度，vlc表示光速，β为太阳光线与系统的夹角，Csr和Cdr表示系统表面的镜面反射和漫反射系数，un和ut表示系统表面法向和光线投影方向的单位矢量。同样方法，可得到太阳光压力在广义坐标ϕ方向作用于主卫星刚体、子卫星刚体及系绳的摄动力矩：

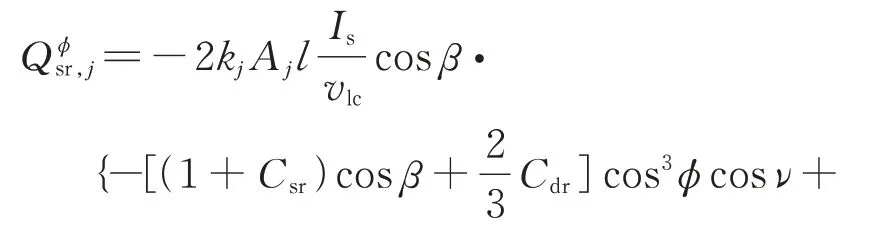
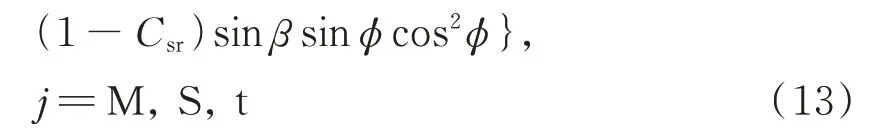
故相应的由太阳光压引起的广义力Qϕsr=为：

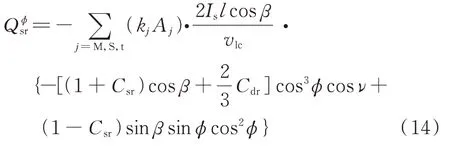
将式（11）和（14）代入广义力表达式Qϕ=Qdϕ+，则系统无量纲动力学方程（5）可改写为：

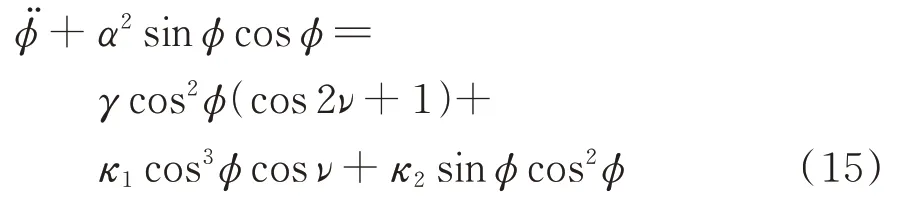
式中

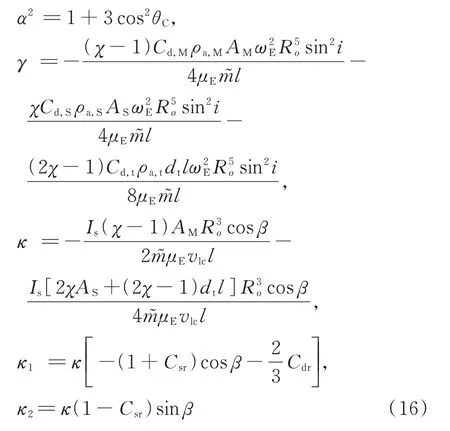
至此，完成了空间环境摄动激励下非轨道面滚转绳系卫星系统模型的构建。显然，这是一个非自治的单自由度非线性系统。

3 混沌的必要条件

设向量ϕ=[ϕ1ϕ2]T=[]T，则系统无量纲动力学方程（15）可改写为以下状态方程形式：

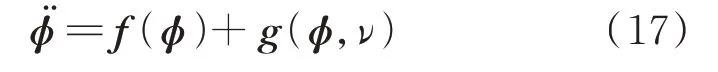
其中向量场和摄动项的具体表达式为：

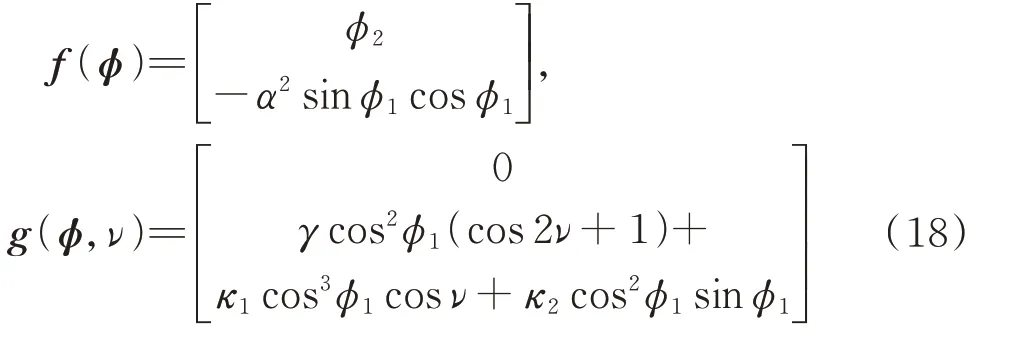
不难看出，摄动项g(ϕ，ν)的周期为2π，即有g(ϕ，ν)=g(ϕ，ν+2π)。值得注意的是，当系统不考虑摄动激励，即g(ϕ，ν)=0 时，其为一个Hamilton 系统，能够计算出系统存在鞍点(∓π 2，0)和异宿轨道：

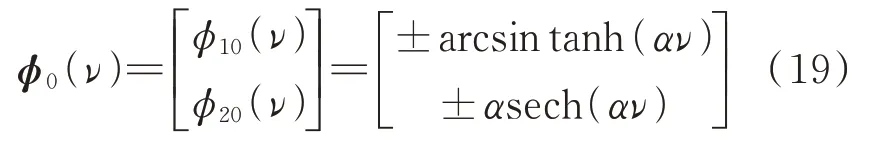
将以上异宿轨线代入以下Melnikov 函数：

有

易见，在周期时间内ν0∈[0，2π]，若系统满足条件：

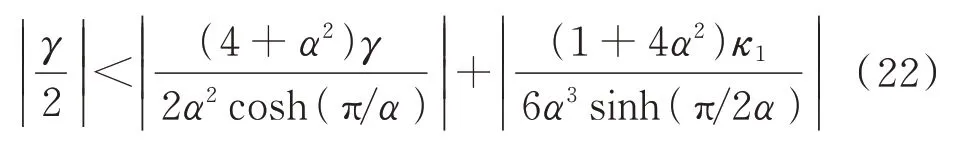
则Melnikov 函数存在简单零点。此必要条件意味着在充分小摄动下，因系统异宿轨道（19）破缺导致稳定流形与不稳定流形在鞍点附近横截相交，这可能诱发Smale 马蹄意义下的混沌运动。

4 数值算例

取以下参数对绳系卫星面外滚转运动进行数值仿真，以揭示系统混沌动力学特性。主星和子星刚体质量分别为mΜ=50 kg 和mS=50 kg，系绳线密度、长度和直径分别为ρt=5×10−3kg/m，l=1 km 和dt=0.5×10−3m。设卫星刚体与系绳的大气阻尼系数皆为Cd，M(S)(t)=2.2，主星和子星刚体的迎风面积分别为AM=1.0 m2和AS=0.3 m2，系统表面的镜面反射系数和漫反射系数分别为Csr=0.8 和Cdr=0.2。

基于解析的混沌判别式（22），对恒定面内俯仰角、轨道倾角、轨道高度构成的有限域内参数(θC，i，Ho)依次取值计算，分析系统是否可能发生混沌，得到如图2（a）所示混沌域，只要参数在此域内，系统将可能发生混沌。选取截面Γ1={(θC，i，Ho)|θC=0 }和Γ2={(θC，i，Ho)|θC=3π 8 }，揭示恒定面内俯仰角θC对混沌域的影响，如图2（b）所示，可以看出面内俯仰角越大混沌域越小。选取截面Γ3={(θC，i，Ho)|i=π 8 }和Γ4={(θC，i，Ho)|i=3π 8 }，图2（c）呈现了轨道倾角i对混沌域的影响，混沌域随轨道倾角增大而缩小。同样，图2（d）为轨道高度Ho对混沌域的作用，随着质心轨道升高混沌域将变大。

进一步，以子星质量、大气阻尼系数、漫反射系数为例，研究系统结构参数、大气阻尼、太阳光压对混沌域的影响。基于初始设定参数，分别将子星质量改设为mS=40 kg、大气阻尼系数改设为Cd，M(S)(t)=1.0、漫反射系数改设为Cdr=0.6，能够看出图3（a），（b），（c）与图2（a）所示混沌域存在差异。可以发现，混沌域对子星质量极为敏感，大气阻尼、太阳光压对混沌域的影响也不可忽略，这些参数对绳系卫星的动力学设计至关重要。

图2 参数(θC，i，Ho)的混沌域Fig.2 Chaotic domain governed by parameters(θC，i，Ho)

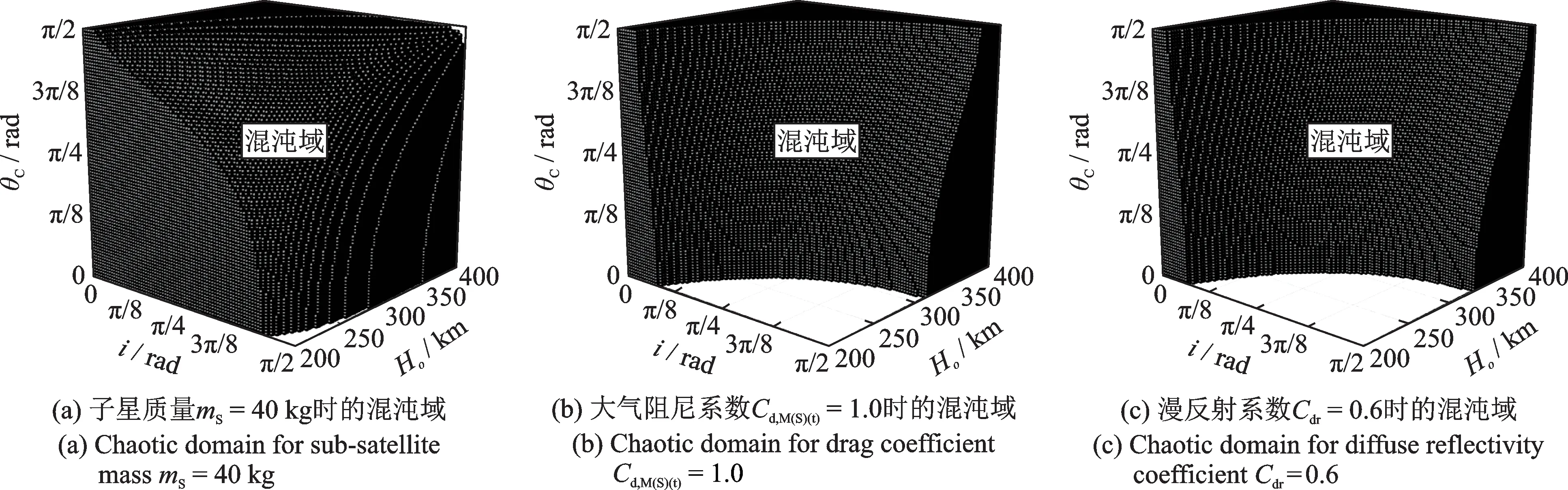
图3 系统参数对混沌域的影响Fig.3 Effect of system parameters on chaotic domain

令系统的恒定面内俯仰角、轨道倾角和轨道高度分别为θC=π 4，i=π 8 和Ho=350 km，进行动力学模拟。可计算出当前系统参数位于混沌域内，即满足混沌判别式（22），有|γ2|=1.1321×10−6<2.8554×10−6。绳系卫星系统的非轨道面滚转运动数值结果如图4所示。图4（a）表示系统面外滚转角的时间历程，可以清楚地看到滚转角呈现非周期变化，故这必然是一个不规则运动。图4（b）为滚转运动的Poincaré 截面，能够观测到在不稳定鞍点附近有大量的横截异宿点存在，这是异宿轨道破缺所致，极易导致混沌发生。图4（c）为系统的功率谱密度，其在(0，0.2 Hz)范围内存在密集的功率谱（这意味系统遍历无穷多个不稳定周期轨道），这是混沌运动的重要特征。图4（d）为系统的最大Lyapunov 指数，其随无量纲时间变化且始终大于0。综合以上结果可以判断，当前系统的面外滚转运动具有非常明显的混沌动力学特性。

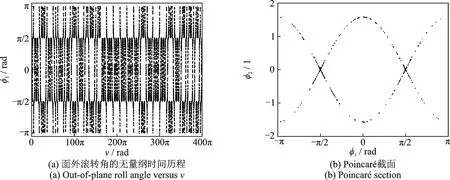
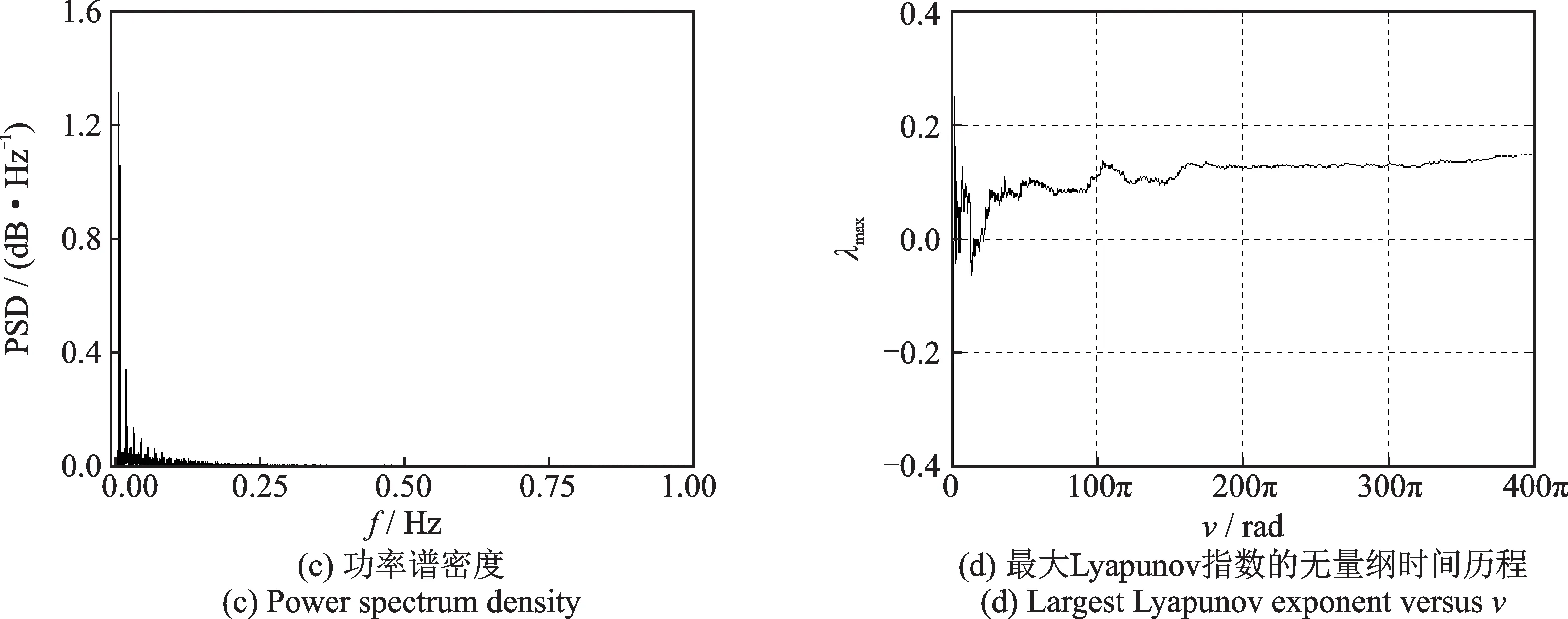
图4 具有混沌特性的面外滚转运动Fig.4 Out-of-plane roll motion with chaotic characteristics

作为对比算例，将系统质心的轨道高度改设为Ho=250 km，其他参数保持不变，则系统参数不再满足混沌判别式（22），即|γ2|=9.1034×10−6>6.4413×10−6。此时，系统的滚转动力学行为如图5所示。从图5（a）可以发现，面外滚转角变化看似具有一定周期性，而图5（b）中Poincaré 截面上的闭轨线则表明此滚转运动具有概周期特性。在图5（c）和5（d）中，功率谱密度的几个孤立尖峰（这意味系统存在固有频率比为无理数的几个不稳定周期运动）和系统最大Lyapunov 指数最终趋于0，进一步说明系统做概周期运动。在此算例中，混沌现象没有出现，这与混沌判别式（22）的判定结果一致。

图5 具有概周期特性的面外滚转运动Fig.5 Out-of-plane roll motion with quasi-periodic characteristics

5 结 论

本文通过正交方向抑制面内俯仰角以保持绳系卫星面内俯仰角恒定，研究环境激励下系统面外滚转非线性特性。基于Melnikov 方法，判定稳定流形与不稳定流形在鞍点附近是否可能横截相交，推导出系统面外滚转的混沌判别式。获得具有动力学指导意义的参数混沌域，其对子星质量等系统参数具有敏感性，并在域内外分别发现混沌、概周期现象。