多维性能极限状态下概率地震需求分析的多元相关核密度估计法
贾大卫,吴子燕,何 乡
(西北工业大学力学与土木建筑学院,陕西 西安 710129)
引 言
由于地震激励具有较强的不确定性,结构的抗震性能通常采用概率评估方法。美国太平洋地震工程研究中心(PEER)对此进行了大量研究,率先提出新一代“基于性能的地震工程(PBEE)”概率决策框架;吕大刚等[1]提出了第二代PBEE 理论。该理论的基础为概率地震需求分析,主要用来计算在具体场地下结构在设计年限内超过给定性能极限状态的结构需求年平均超越概率。地震需求将场地危险性与结构地震易损性相结合,其含义是对所有地震风险事态作用下所对应的结构需求概率的积分。
国内外学者开展了大量有关概率地震需求分析的研究,并取得了丰硕的成果。钟剑等[2]基于全概率理论进行了桥梁结构的地震风险分析;Liu 等[3]将结构阈值视为凸集变量,建立了一种基于凸集-概率混合可靠度模型的概率地震需求分析方法;Khorami 等[4]基于增量动力分析法,得到了钢框架结构的地震易损性曲线;Banihashemi 等[5]考虑了结构的整体性能,进行了钢框架的地震易损性和可靠性分析;蒋亦庞等[6]考虑结构参数的不确定性,建立了无筋砌体结构的地震易损性曲线,并探讨了结构参数的不确定性对结构性能的影响;Khaloo 等[7]采用桥墩柱的最大弯曲延性响应建立了桥梁结构的易损性曲线,并且考虑了时变损伤效应。但上述研究存在一些不足:其一,部分研究仅基于一维工程需求参数(EDP)进行分析,而未考虑多种EDP 的联合作用,结构在地震激励下破坏形式比较复杂,仅考虑一种参数难以准确得到失效概率;其二,绝大多数研究仅考虑了结构易损性,而并未涉及场地危险性分析,因此所得结论并不完整;其三,在传统概率地震需求分析中,普遍采用基于对数正态分布假定的理论分析法,即将结构EDP 视为服从对数正态分布的概率随机变量,该假定使用方便,但具有一定局限性。Mangalathu 等[8]通过Kolmogorov-Smirnov 非参数检验法,验证了桥梁结构的EDP 拒绝服从对数正态分布;Cornell 等[9]认为桥梁各构件的易损性曲线并非全部满足对数正态分布假定;Karamlou 等[10]认为对数正态分布假定会引起结构易损性分析结果的不准确;袁万城等[11]认为部分EDP 和地震强度之间不满足对数线性回归的假设。上述研究表明,对数正态分布假定并不完全适用于任意结构,可能会导致分析结果产生较大误差。
为得到更加可靠的抗震性能评估结果,董俊等[12]和单德山等[13]提出了基于核密度估计的分析方法。该方法不需要人为假定EDP 分布类型,并且得到的易损性曲线与蒙特卡洛(MC)法更为接近。但文中仅针对单一EDP 建立了易损性曲线,没有考虑多种EDP 联合作用下结构的破坏形式;并且文中仅涉及了地震易损性,并未考虑场地危险性,因此研究内容并不完善。本文考虑结构的多维性能极限状态,提出基于多元核密度估计的概率地震需求分析法。这种方法不对EDP 的分布类型进行人为假定,并在传统核密度估计中引入对随机变量相关性的描述,使结果更具一般性。以某RC 框剪结构为例,首先利用多维性能极限状态方程衡量结构在地震激励下的损伤程度;然后不采用对数正态分布假定,而是利用多元相关核密度估计建立概率地震需求模型;最后利用MC 模拟得到结构需求的年平均超越概率。将本文方法与传统方法进行对比,突出其差异性。
1 核密度估计
核密度估计是一种非参数估计法,主要用于得到参数的概率密度函数。该方法主要优势是:不需要对数据的分布类型进行人为假设,只需要确定输入数据、核函数以及带宽就可以估计出变量的概率密度函数。当仅考虑一维变量时,核密度估计如下式所示:
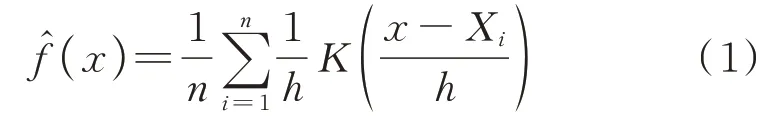
式中代表概率密度函数;n为样本容量;h为带宽;Xi代表样本点;K( ⋅)为核函数。核函数需要具备如下属性:
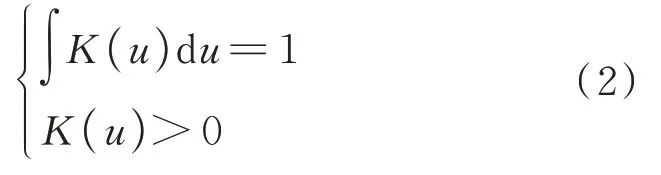
核函数具有多种形式,包括均匀型、三角型、高斯型等。目前使用最广泛的核函数为高斯型核函数[14],如下式所示:
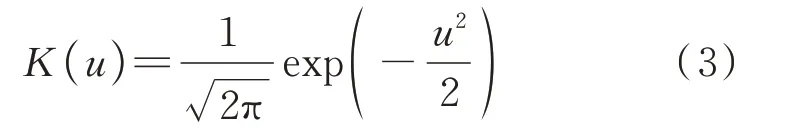
当随机变量由一维拓展到m维时,联合概率密度函数f(x)=f(x1,x2,…,xm)。文献[14]给出了多元随机变量的核密度估计表达式,如下式所示:
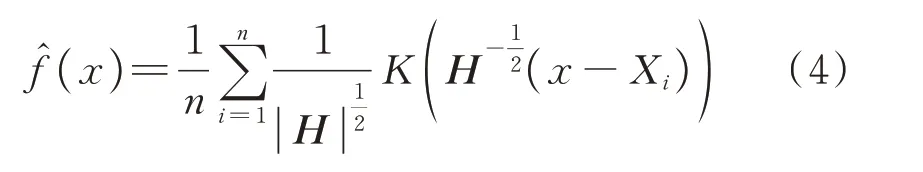
式中H为带宽矩阵,是一个m×m维的对称正定矩阵。一般可将H取为对角阵,即:
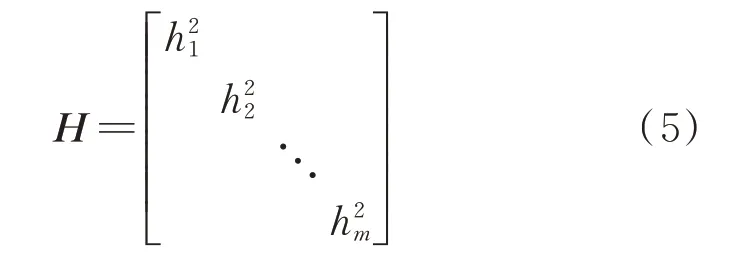
式中hi,i=1,2,…,m代表单随机变量核函数的带宽,可采用下式计算[15]:

式中σi为第i个随机变量的标准差。
则式(5)可写为:
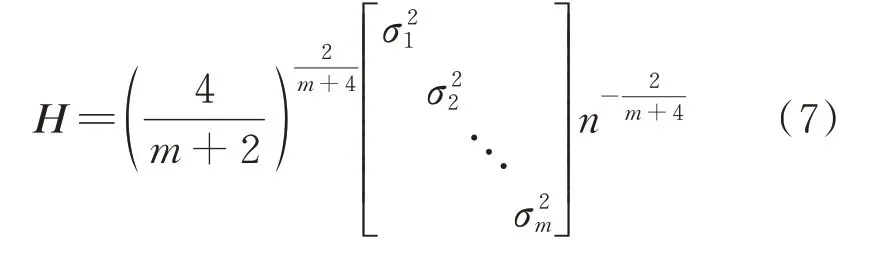
将式(5)代入式(4),并取高斯型核函数用于多元核密度估计。已有研究表明[15-16],当采用高斯核函数时,多元核密度估计的核函数可以表示为多个单随机变量核函数乘积的形式。以二维随机变量为例,在式(7)中有m=2,多元核密度估计可写为:

已有文献表明[14],不同核函数对核密度估计的影响较小,但带宽影响很大。式(8)采用固定带宽,即每个数据点处都有着相同的带宽,然而由于数据的随机性较强,固定带宽的核密度估计可能误差较大,因此大多采用基于自适应带宽的核密度估计法[15-17]。本文采用文献[15]提出的自适应带宽,即:
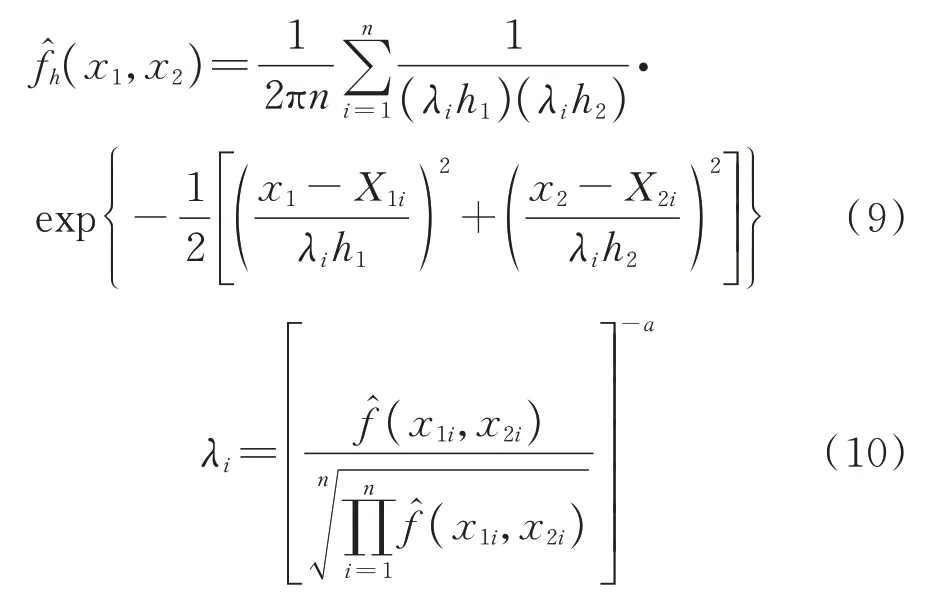
式中(x1,x2)为自适应带宽的核密度估计;a为敏感性参数,通常可取0.5;λi代表带宽的自适应修正系数;(x1i,x2i)为固定带宽时的核密度估计。
式(8)和(9)给出的多元核密度估计得到了广泛应用,但其最大的缺陷在于并不能考虑随机变量的相关性。在概率地震需求分析中,不同EDP 通常并不完全独立。例如桥梁结构桥墩柱的弯曲扭转角和支座位移通常具有相关性[18],框架结构最大层间位移角(MIDR)和最大层加速度(PFA)也并不完全独立[19]。因此本文提出可以考虑随机变量相关性的多元核密度估计法,下面将详细论述。
2 考虑变量相关性的多元核密度估计
2.1 多元相关核密度估计
由于自适应带宽的核密度估计源于固定带宽,因此首先考虑相关性条件下固定带宽的计算。为方便表示,以下均采用二维变量论述。取随机变量的相关系数为ρ,并代入式(7),有:
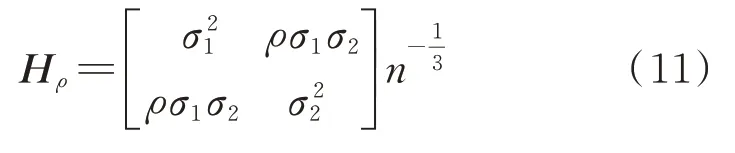
此时带宽矩阵并不为对角阵。对角线上的元素与传统核密度估计的一致,反映了单变量的带宽,而除对角线以外位置的元素则体现了随机变量的相关性。
由式(8)和(4)可知,当取高斯型核函数时,多元核密度估计的核函数可以表示为多个核函数的乘积,其形式与多元高斯分布十分相似。这里首先对多元高斯分布做简要介绍,如下式所示:
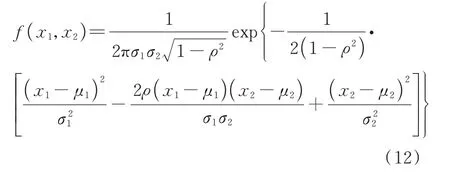
式中μ1和μ2分别代表正态随机变量x1和x2的均值;σ1和σ2代表标准差。
若假定随机变量相互独立,式(12)简化为:

比较式(13)和(8)可知,式(8)中指数函数幂的形式与式(13)中指数函数幂的形式完全一致。因此本文在多元核密度估计的核函数中引入相关系数。当采用固定带宽时,式(8)中可重新表示为:
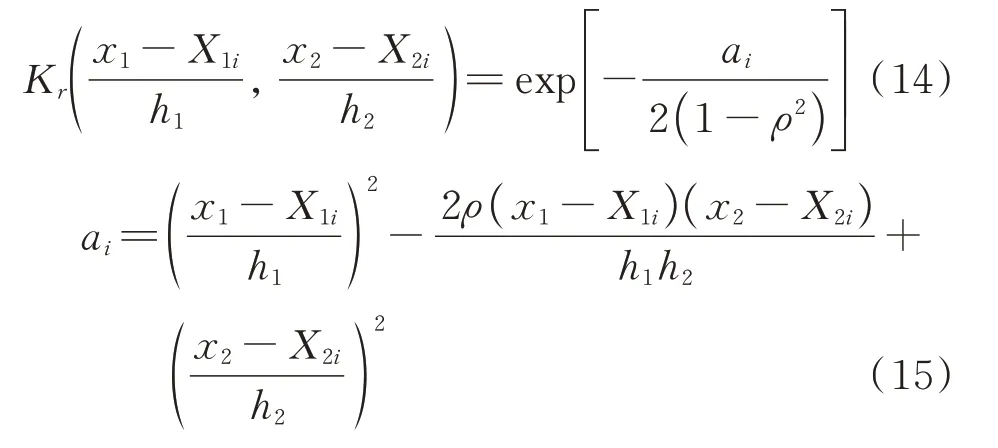
其次,用Hρ替代H,且有:
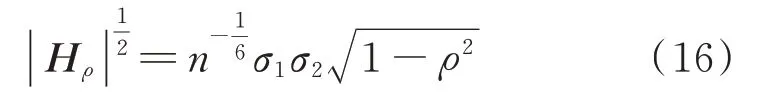
联立式(8)和式(12)~(16),可得在固定带宽下基于相关性的多元核密度估计,如下式所示:
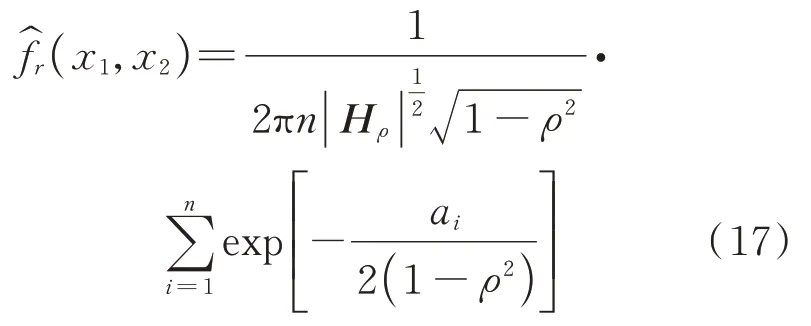
由式(17)可知,本文建立的多元核密度估计函数主要从带宽矩阵和核函数两个方面体现随机变量的相关性。在带宽矩阵中引入项,而在传统基于多个高斯型核函数相乘的多元核函数中也引入了相关高斯分布的形式,从而将随机变量的相关性引入核密度估计中。
下面考虑自适应带宽的相关核密度估计,将自适应修正系数λi代入式(11),有:
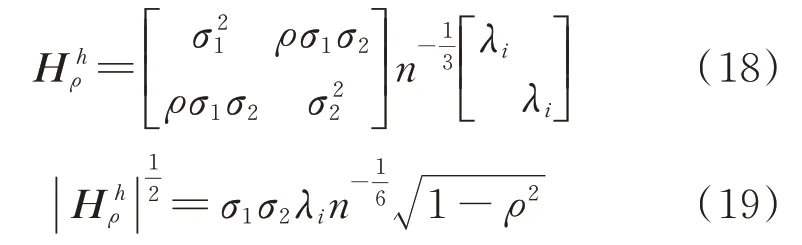
相应的式(15)变为:
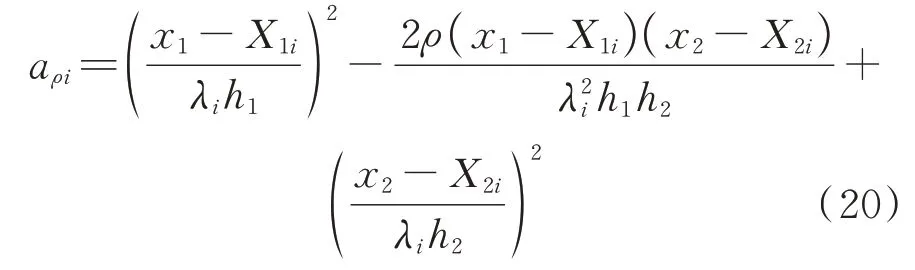
则自适应带宽的相关核密度估计表示为:

其中,λi的计算方法与式(10)一致,在相关性的条件下固定带宽的核密度估计采用式(17)计算。
式(21)即为本文最终建立的基于相关性的多元自适应核密度估计公式。当ρ=0 时,式(21)变化为传统不考虑相关性的多元核密度估计公式。利用式(21)建立多维概率地震需求模型即可避免对数正态分布假定,并且可以考虑EDP 之间的相关性。
2.2 随机变量相关性的描述
当给出了多元相关核密度估计的表达式后,如何确定相关系数就成了关键问题。目前相关系数主要包括Pearson 相关系数,Spearman 相关系数和Kendall 相关系数[20]。Pearson 相关系数ρp用于分析两组数据是否可以用一条直线拟合对应关系,衡量二者的线性相关度,取值在[−1,1]之间。在三种相关系数中,Pearson 相关系数目前应用最广。若无特别声明,相关系数一般都指Pearson 相关系数。若Pearson 相关系数的绝对值在0.8~1之间时,说明两个变量的相关性较强。若绝对值低于0.4,认为两组数据相关性很弱,如下式所示:
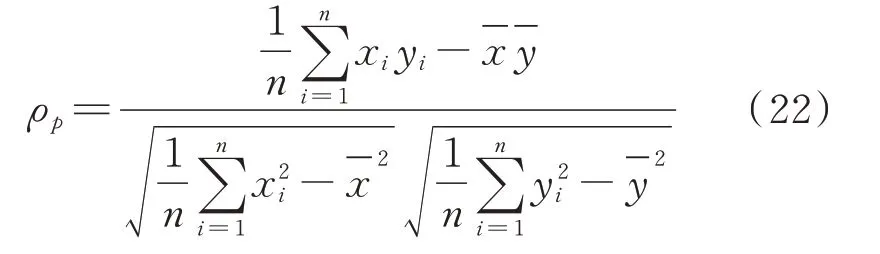
式中xi和yi为数据值;和为两组数据集的均值。
Spearman 相关系数ρr主要通过单调方程评价两组变量的相关性,可用来描述变量之间的非线性关系。Spearman 相关系数的取值同样大于−1 且小于1,如下式所示:

式中Ri代表xi的秩次;Qi代表yi的秩次。
Kendall 相关系数ρτ是一种等级相关系数,从变量单调相依的角度定义两个变量之间的相关性,根据两个变量所包含的样本是否具有和谐性判断两组变量是否具有相关性,如下式所示:
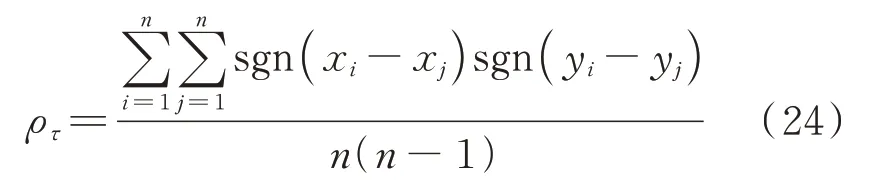
式中 sgn(·)为符号函数。
3 基于多维性能极限状态的概率地震需求分析
3.1 易损性分析
概率地震需求分析包含两部分内容:结构易损性分析和场地危险性分析,是指在考虑场地风险的情况下,结构发生不同损伤程度的可能性[21]。其意义在于:既采用概率方法计算结构在不同地震强度下的破坏概率,又考虑场地危险性,将二者卷积,得到结构需求的年平均超越概率。其中多维性能极限状态描述了多种EDP 联合作用下结构的极限状态[22],可通过多维性能极限状态方程描述,如下式所示:
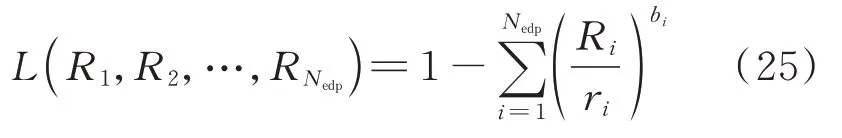
式中L为多维性能极限状态方程,当L<0 时认为结构发生破坏;Nedp为EDP 个数;R代表EDP;r代表EDP 在对应性能极限状态下的阈值;b为相互作用因子,决定了极限状态曲面的形状。
黄小宁等[23]指出,在两种EDP 的条件下,可将一个EDP 的b简化为1,如下式所示:
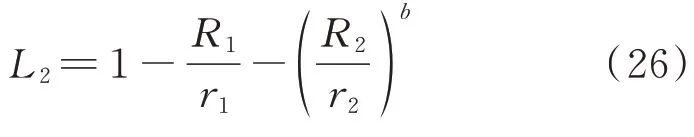
以两种EDP 为例,在多维性能极限状态下,易损性表示为EDP 的概率密度函数在失效域内的积分,如下式所示[19]:
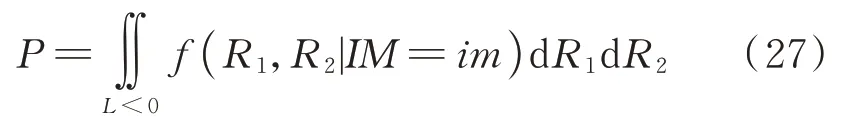
式中IM=im代表给定的地震强度;f( ⋅)代表随机变量的联合概率密度函数。在本文中f( ⋅)由多元相关核密度估计,即式(21)得到,而并非传统的多维对数正态分布。
韩建平等[24]指出,对城市内基础设施而言,绝大多数建筑结构的抗震性能通常受到结构构件和非结构构件的共同影响,并且实际使用功能绝大多数都依赖于非结构构件。而传统基于一维EDP 的地震易损性函数仅能考虑结构构件性能,例如框架结构一般采用最大层间位移角(MIDR)来衡量结构构件的损伤,桥梁结构则大多采用墩柱扭转角或相对位移延性比。而式(27)可以考虑不同EDP 作用下结构的联合性能极限状态,因此更符合实际需求。
3.2 概率地震需求分析
Liu 等[19]指出,在多维性能极限状态下,结构需求表示为地震易损性和场地危险性的耦合形式,其结果为设计年限内结构需求在给定极限状态下的年平均超越概率,可用如下三重积分公式表示:

式中EIM(im)代表地震强度的累积分布函数。
国内目前建筑结构抗震设防的依据为抗震设防烈度,有资料表明,采用极值Ⅲ型分布描述地震烈度的概率分布比较符合国内的实际情况[21],分布函数如下式所示:

式中w为地震烈度上限,可取为12;ε为众值烈度,表示年平均发生概率为0.632 的地震烈度;K为形状参数,一般采用最小二乘法确定。式(29)也被称为地震危险性函数。
3.3 基于蒙特卡洛模拟法的年平均超越概率计算
由式(28)可知,在概率地震需求分析中需要求解多重积分。由于引入了多元相关核密度估计,这个积分相比传统多维对数正态分布的被积函数更为复杂。因此本文引入蒙特卡洛(MC)模拟以提高计算效率。谷音等[21]指出,若地震强度的分布函数已知,可通过抽样将地震危险性函数进行离散。假定抽取的地震强度样本个数为nim,则每个样本出现的概率为1/nim。谷音等[21]在一维EDP 条件下,提出了结构需求年均超越概率的MC 法,如下式所示:

式中imi为抽样所得单个地震强度样本;而P(R>r|imi)则反映了在该地震强度样本下结构的破坏概率。
但式(30)只考虑了一维EDP,本文将式(30)推广到多维性能极限状态下的概率地震需求计算。将式(30)代入式(28),可得:
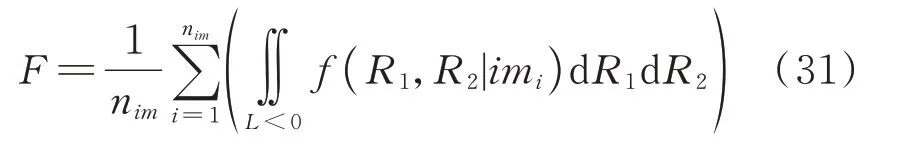
由式(27)可知,多维性能极限状态下易损性分析的本质是在给定EDP 分布的条件下计算性能极限状态方程小于0 的概率,因此同样可采用MC 法求解。失效概率表示为:
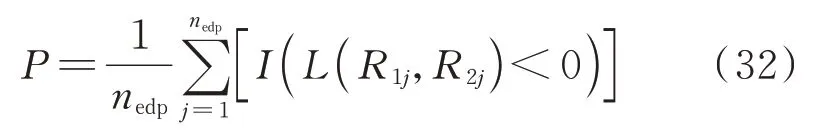
式中 (R1j,R2j)代表基于多元相关核密度估计构造的概率地震需求模型抽样获得的样本;nedp代表生成的结构响应样本点总数;I( ⋅)代表指示函数,当L(R1j,R2j)<0 时,I( ⋅)=1,反之为0。将其代入式(31),有结构需求年平均超越概率:
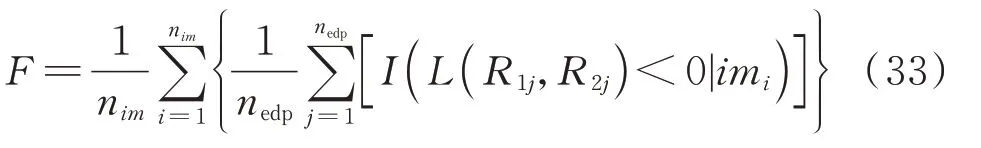
式(33)即为本文最终建立的基于多元相关核密度估计的概率地震需求分析公式。考虑到多变量相关的核密度估计结果比较复杂,本文采用文献[14]建议的舍选抽样法获得(R1j,R2j)样本。假定随机变量的取值域为[a,b],f(R1,R2)的极大值为M,舍选抽样法流程如图1所示。
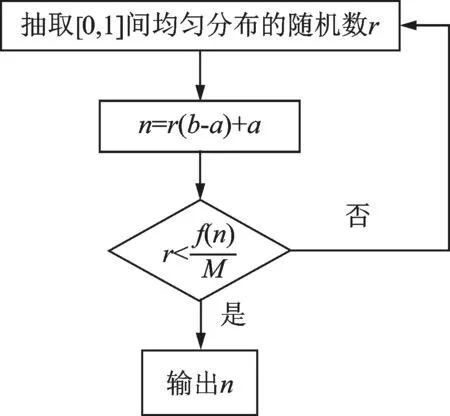
图1 舍选抽样法Fig.1 Acceptance-rejection sampling method
与Liu 等[19]和谷音等[21]提出的概率地震需求分析方法相比,本文所提方法的特点在于:考虑了多个EDP 下结构的多维性能极限状态,多维概率地震需求模型由多元核密度估计法确定,而不需要对EDP进行对数正态分布假定;并且在传统多元核密度估计的基础上提出了可以考虑随机变量相关性的核密度估计法,进而将EDP 的相关性引入概率地震需求分析。基于多元相关核密度估计的概率地震需求分析流程如图2所示。
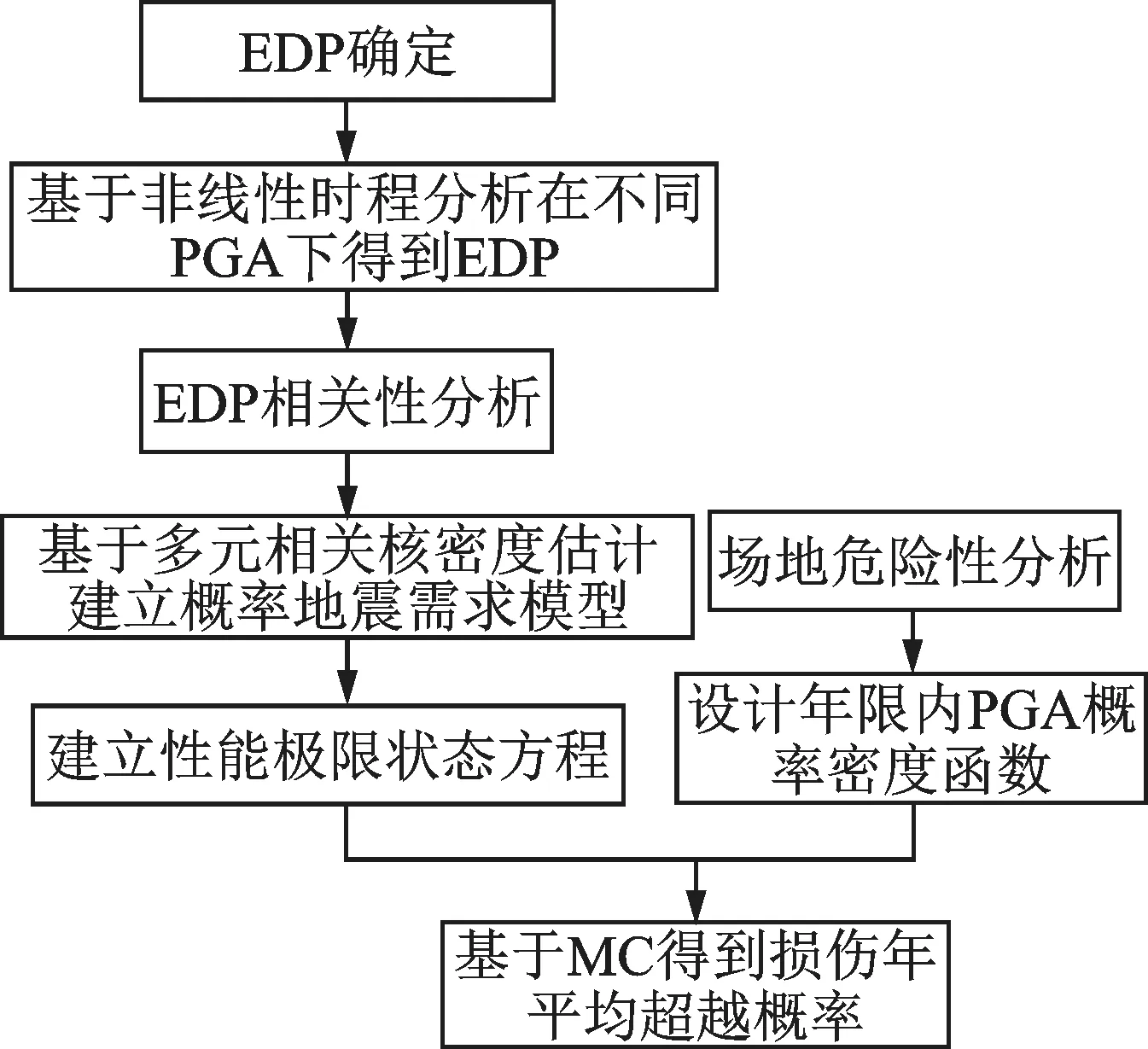
图2 概率地震需求分析流程图Fig.2 Flow chart of probabilistic seismic demand analysis
4 算例分析
4.1 结构模型建立及工程需求参数确定
本文基于SAP2000 建立某RC 框架-剪力墙结构,沿X方向共5 跨,跨度均为8 m;沿Y方向共3 跨,边跨跨度为6 m,中跨跨度为8 m。沿Y向主梁间设置单根次梁。该结构共4层,各层层高均为3.6 m。抗侧力体系由混凝土框架和剪力墙部分组成。剪力墙部分包括两片单肢剪力墙及由两个电梯井组成的核心筒,核心筒长8 m,宽4 m,门洞高2.4 m,宽2 m。各构件采用的混凝土强度等级均为C30,纵向受力钢筋采用HRB400 级,箍筋采用HRB335。楼板厚度为120 mm,配筋为单排钢筋,采用HRB335 级钢筋。剪力墙厚度为300 mm,结构模型如图3所示。梁和柱均采用SAP2000中的Frame单元模拟,并在梁两端布置P-M3 铰,柱两端布置P-M2-M3 铰。剪力墙采用分层壳单元[25],为提高计算效率,仅考虑混凝土层和钢筋层在竖向的非线性行为,混凝土层面外仅考虑线性行为,剪力墙采用分层壳单元,在三个应力分量上均考虑其非线性行为。混凝土楼板采用Membrane 单元。此外,模型考虑了P-Δ 效应,阻尼采用瑞利阻尼。本文采用的混凝土和钢筋的本构关系如图4所示。
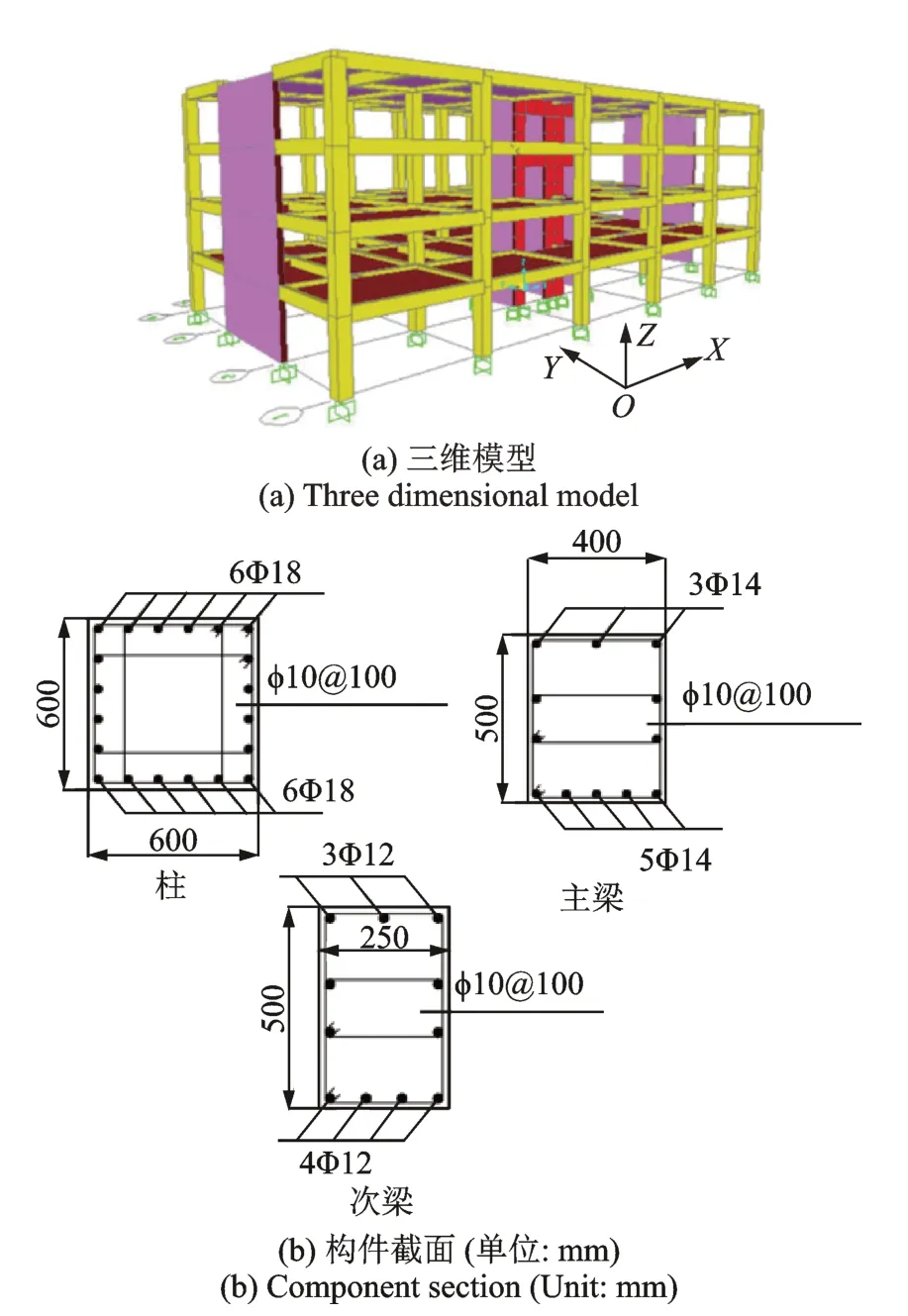
图3 结构模型Fig.3 Structure model

图4 材料本构关系Fig.4 Material constitutive relationship
在基于性能的地震工程研究中,通常将结构的性能极限状态划分为若干等级。参考文献[22],本文将性能极限状态分为“正常使用(NO)”,“可以使用(IO)”,“生命安全(LF)”,“防止倒塌(CP)”四级。
确定了性能极限状态,下一步将确定EDP 及对应性能极限状态的阈值。有文献表明[24-26],MIDR 能较好地反映结构构件的整体损伤大小,因此本文选择最大层间位移角(MIDR)作为衡量结构性能的EDP。郑山锁等[26]指出,结构整体性能水平达到IO时构件处于开裂状态,MIDR 的阈值大致取LF 的50%;LF 的阈值大致取到规范弹性限值和弹塑性限值的平均值;CP 大致取到规范的弹塑性变形限值的90%。基于《建筑抗震设计规范》[27],本文采用的MIDR 阈值如表1所示:
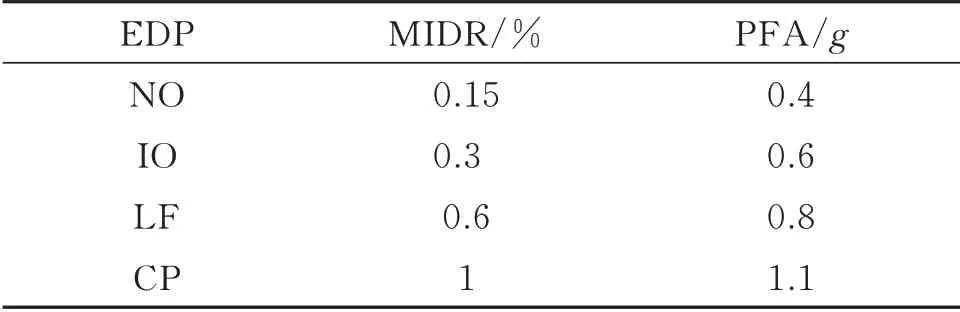
表1 EDP 阈值Tab.1 EDP thresholds
已有研究表明[24,28],在考虑非结构构件的损伤时,主要考虑对加速度敏感的构件,例如机械设备、内部管道等,因而本文选择最大层加速度(PFA)作为衡量非结构构件损伤大小的EDP。本文取文献[24]中建议的PFA 阈值,如表1所示。表中g=9.8 m/s2。在这里指出,MIDR 阈值来自《建筑抗震设计规范》中对弹性MIDR 和弹塑性MIDR 阈值的规定,能够比较准确地反映结构构件的性能极限状态。而PFA 主要影响内部设备的正常工作,且目前国内并没有统一的规范对不同类型结构的PFA 阈值进行规定,因此本文采用已有研究给出的经验阈值。
4.2 地震危险性分析
拟定该框架所处的场地特征参数如下:场地土类别为I,抗震设防烈度为7 度,设计基本地震动加速度为0.1g,场地特征周期为0.35 s,结构的阻尼比取0.05,周期折减系数为0.9,设计基准周期为50年。本文仅考虑设计年限内的场地危险性,设防烈度对应50年内超越概率为10%的烈度。50年内众值烈度为7−1.55=5.45 度[21],则有:
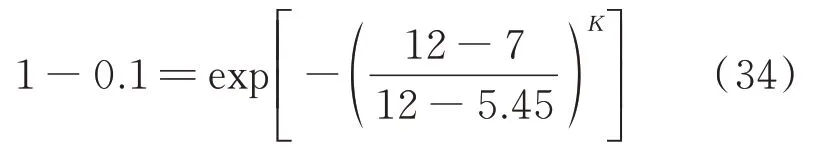
通过最小二乘法可得形状参数K约为8.3189,则50年内地震烈度的分布函数为:
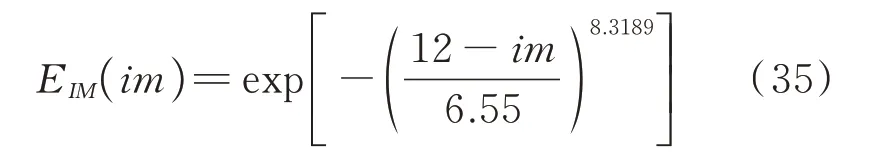
在地震工程学中,峰值地面加速度(PGA)是衡量地震强度的关键指标之一[18-19]。本文选择PGA衡量地震强度的大小,因此需要将地震烈度换算为PGA,采用谷音等[21]给出的换算公式,如下式所示:
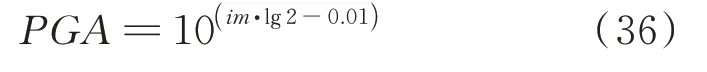
将式(36)代入式(35),并将PGA 的单位用g表示,可得PGA 的累积分布函数为:
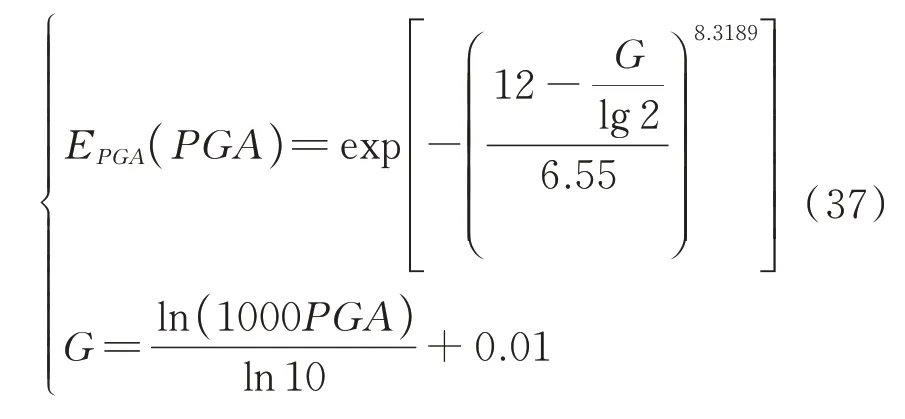
分别对式(35)和式(37)两端求导,可得地震烈度和PGA 的概率密度函数曲线。由于PGA 累积分布函数形式比较复杂,在MC 模拟中,首先根据式(35)生成nim个地震烈度样本,然后将这些样本根据式(36)转化为 PGA 样本。本文取nim=10000,抽得地震烈度和转化后的PGA 样本分布及其概率密度函数曲线如图5和6所示。由图可知,生成的PGA 样本与概率密度函数拟合度较高。由于地震烈度和PGA 的分布函数是根据结构设计年限得到的,因此生成的样本能在考虑场地类型的前提下,较全面地反映设计年限内地震强度的随机性以及不同强度地震发生的可能性。概率密度值越大,表明设计年限内发生的可能性越大。
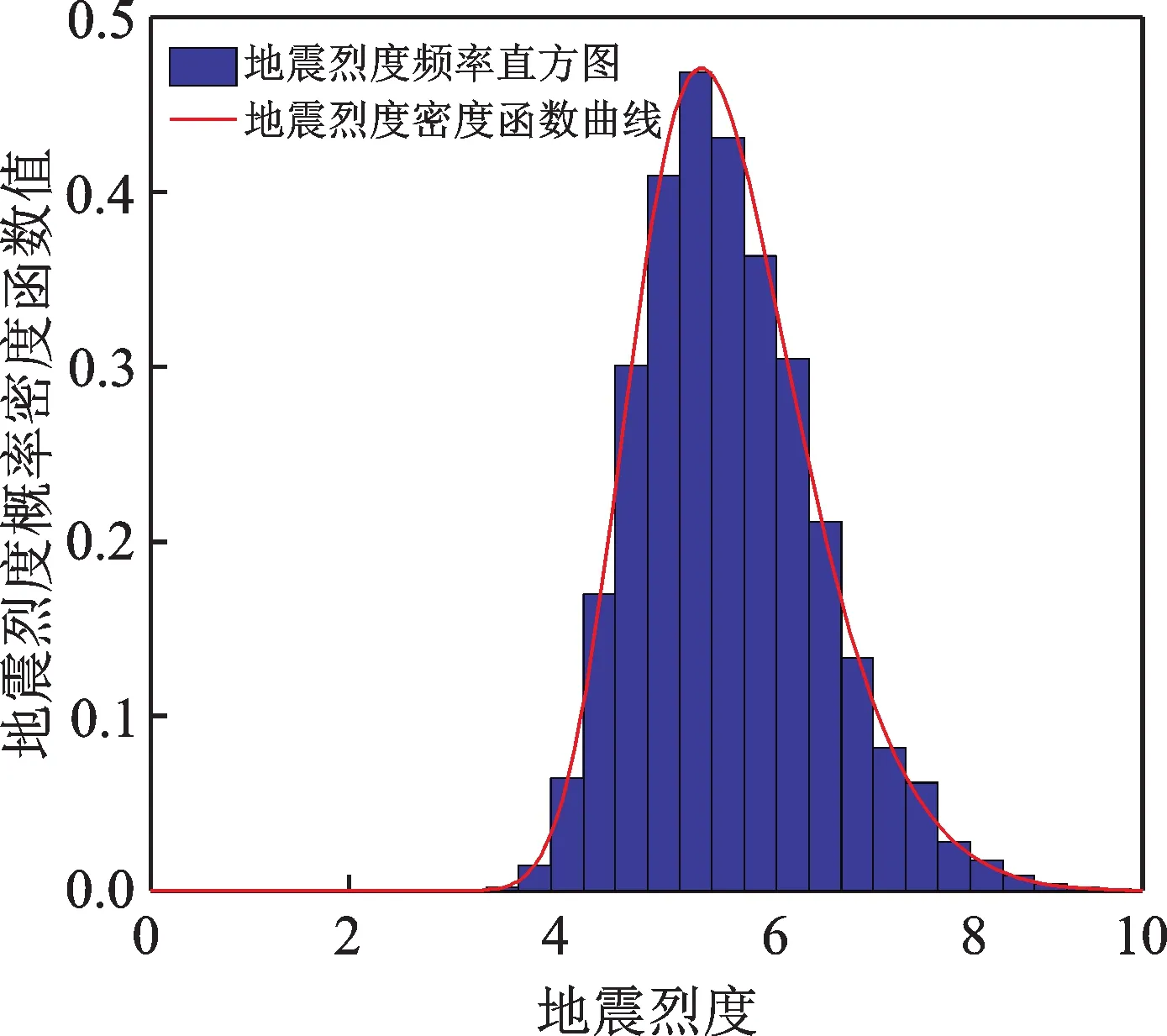
图5 地震烈度分布Fig.5 Distribution of seismic intensity
4.3 地震激励不确定性
已有研究表明,在地震需求分析中,需要选择多于20 条地震波衡量地震激励的不确定性[29]。本文采用文献[30-31]建议的基于Simqke 理论的合成地震动进行地震需求分析。根据4.2 节中定义的场地特征,从SAP2000 中可提取规范反应谱,将其作为目标反应谱,然后基于Simqke 理论合成了40 条地震波用于地震风险分析。这些地震波的加速度平稳段开始时间为0.02 s,加速度平稳段的持续时间为25 s,地震波持续时间为40 s。地震波的反应谱如图7所示。图中红线代表目标反应谱,蓝线代表地震波加速度反应谱。由图7可知,地震波的反应谱与结构所处场地的目标反应谱拟合度较高。

图7 地震波反应谱Fig.7 Response spectrum of seismic wave
4.4 基于核密度估计的多维概率地震需求模型建立
获得概率地震需求模型是进行地震风险概率分析的关键步骤。基于本文提出的多元相关核密度估计,概率地震需求模型需要在不同PGA 下通过式(21)获得。
由图6可知,生成的PGA 样本绝大多数位于区间[0,0.1g]中,说明强度位于这个区间的地震50年内发生的可能性较大。因此为准确反映当PGA<0.1g时结构的损伤情况,在等步长调幅法[32]基础上,本文提出一种分段等步长调幅法。首先将每条地震波的PGA 分别调幅至0.02g~0.1g,间隔取0.02g,然后在区间[0.1g,1.0g]间进行调幅,间距取0.1g,最终得到560 条地震波。Zhou 等[32]指出,地震发生时,地面运动是一个三维随机过程,在地震工程研究中考虑三维地震动输入更符合实际。本文将每条地震波的输入方向均设置为空间三维,加载方式为1*X+0.85*Y+0.65*Z[32]。利用SAP2000 进行非线性时程分析,得到每条地震波在各个PGA 下的MIDR 和PFA。利用式(21),分别在不同PGA 下基于三种相关系数建立基于核密度估计的概率地震需求模型。为对比相关性对模型的影响,本文同样建立基于不考虑相关性的核密度估计概率地震需求模型。以PGA=0.3g为例,如图8所示。
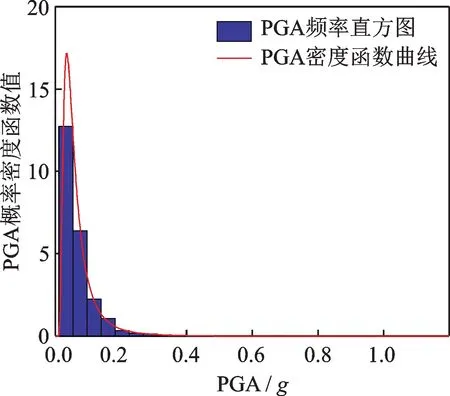
图6 PGA 分布Fig.6 PGA distribution

图8 基于核密度估计的概率地震需求模型Fig.8 Probability seismic demand model based on KDE
由图8可知,考虑EDP 相关性后,概率地震需求模型与不考虑相关性时相比具有一定差异,且不同的相关系数对应的概率地震模型也并不完全一致。首先,考虑相关性后,概率密度函数的峰值显著上升,且有Pearson 系数>Spearman 系数>Kendall系数>无相关性,其中Spearman 系数和Kendall 系数的概率密度峰值差异并不显著。其次,具有明显概率密度函数值的EDP 覆盖范围不一样。当不考虑相关性时,概率地震需求模型在XOY平面上的投影可近似为圆形;而考虑相关性后,投影区域变成具有倾斜角的椭圆,并且具有显著概率密度值的区域面积变小。基于Pearson 系数的投影区域覆盖面积小于Spearman 系数和Kendall 系数,而不考虑相关性时覆盖面积最大。例如以边界MIDR=[0,10−3]和PFA=[3,4] m/s2围成的左上三角区域内,不考虑相关性的核密度估计构造的概率地震需求模型的概率密度值要显著大于Pearson 系数的概率密度值,Spearman 系数和Kendall 系数的概率密度值介于二者之间。因此Pearson 系数对核密度估计结果影响最大,Spearman 系数和Kendall 系数相对较小。
4.5 结构需求年平均超越概率计算
根据式(26)和表1建立性能极限状态方程,以NO 为例,如下式所示:
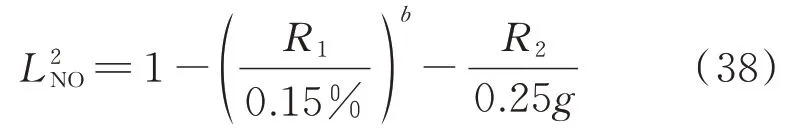
式中R1代表MIDR;R2代表PFA。
在二维极限状态方程中,本文将MIDR 对应的b取为1。由于缺少框剪结构的统计数据,初步拟定PFA 的b=2,后文将通过灵敏度分析讨论b的值对超越概率的影响。利用式(33)基于核密度估计进行地震需求分析,得到结构需求年平均超越概率,并用危险性曲面表示。危险性曲面反映了当EDP 取不同值时的结构需求在设计年限内的年平均超越概率。为对比核密度估计法和传统方法的差异,同样基于多维对数正态分布假定建立危险性曲面。文献[18-19]已经分别给出了多维性能极限状态下基于对数正态分布假定的易损性和概率地震需求分析的详细论述,本文不再重复。危险性曲面如图9所示。
由图9可知,基于Pearson 相关系数的核密度估计危险性曲面位于最上部,基于Spearman 和Kendall系数的危险性曲面整体差异不大,而不考虑相关性的核密度估计的危险性曲面位于最下部。当PFA>0.85g时,核密度估计法和传统方法所得年平均超越概率均基本为0,危险性曲面基本重叠。为定量描述本文所提核密度估计法与传统对数正态分布假定的差异,本文定义一个影响系数λp,如下式所示:
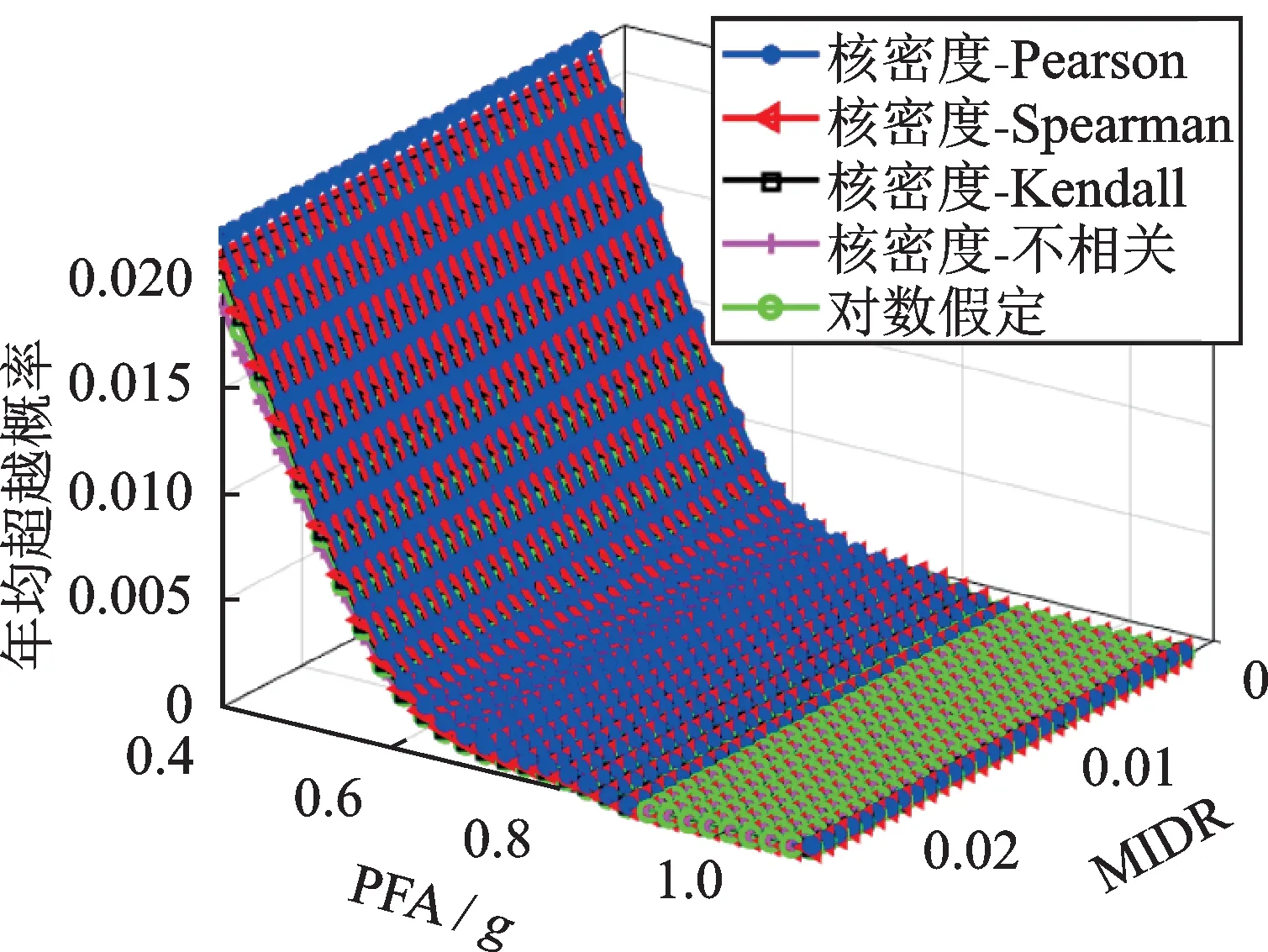
图9 危险性曲面Fig.9 Hazard surface

式中Fkde代表基于核密度估计的年平均超越概率;Flog代表基于传统对数正态分布的年平均超越概率;D代表危险性曲面在XOY平面内的投影区域。
λp绝对值越大,说明二者差异越大。λp如表2所示。

表2 影响系数Tab.2 Influence coefficients
由表2可知,在三种相关系数下,λp均大于0,说明本文提出的基于相关核密度估计的概率地震需求模型得到的危险性曲面更高,结构需求年平均超越概率整体偏大,而对数正态分布假定得到的年平均超越概率偏小。Pearson 系数的λp为0.1219,而Kendall 系数的λp为0.0131,Spearman 系数的λp为0.0308。说明Pearson 系数所得年平均超越概率最大,对核密度估计结果的影响同样最大,Spearman系数次之,而Kendall 系数最小,这个结论与4.4 节所得结论一致。该结论可通过图8和在给定地震强度下结构的失效概率进行解释。以PGA=0.3g和IO性能状态为例,根据式(27)和(32),可得基于Pearson 系数,Spearman 系数和Kendall 系数的结构失效概率依次为0.2115,0.1880 和0.1826,而不考虑相关性时为0.1624。该现象表明:不考虑相关性会得到偏低的失效概率,且在相关性条件下得到的失效概率,Pearson 系数>Spearman 系数>Kendall 系数。在其他PGA 下也可以得到类似的结论。而年均超越概率是根据失效概率得到的,因此三种相关系数对年均超越概率的影响:Pearson 相关系数影响最大,Spearman 相关系数次之,Kendall 相关系数最小。值得注意的是,当PFA 大于0.85g时,对应的PGA大于0.6g。由图6可知,设计年限内发生PGA 大于0.6g地震的可能性很低,因此三种相关系数得到的年均超越概率都很小,对应图9中危险性曲面基本重叠的部分。研究人员可根据实际情况选择不同的相关系数,基于非线性时程分析得到不同的EDP值,根据式(22)~(24)即可进行相关性分析。
如果采用传统不相关的核密度估计法,由表2可知,KDE-Irrelevant 的λp<0,说明不相关核密度估计法得到的危险性曲面低于传统对数正态分布假定,会得到偏低的年平均超越概率。这个结论同样可根据失效概率进行说明。因此在基于核密度估计的概率地震需求分析中,如果不考虑EDP 的相关性同样会得到不准确的评估结果。
4.6 相互作用因子对危险性曲面的影响
相互作用因子b会影响到性能极限状态方程的非线性程度,改变失效域的大小。Wang 等[18]和Liu等[19]对b与结构失效概率的关系在对数正态分布假定下进行了大量研究。本文将利用文献[18]采用的灵敏度分析法,探究相关核密度估计的危险性曲面与b的关系。分别再取b=1,5,10,15,所得危险性曲面如图10所示。由图10可知,当b相同时,三种相关系数下的年平均超越概率从大到小依次为:Pearson 系数,Spearman 系数,Kendall 系数,该结论与4.5 节一致。

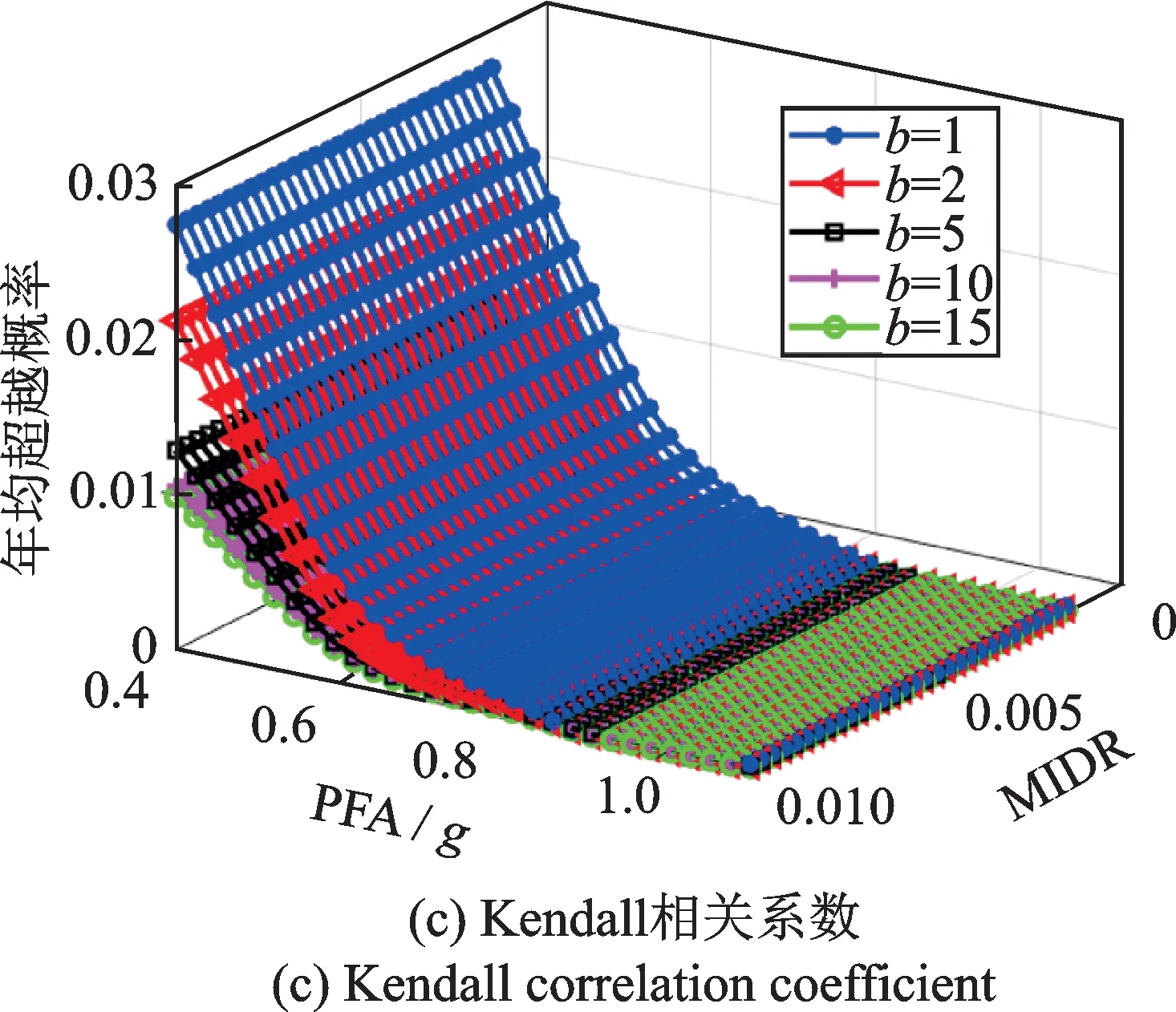
图10 相互作用因子对危险性曲面的影响Fig.10 Influence of interaction factors on hazard surfaces
比较不同b对应的危险性曲面可知,当b=1时,危险性曲面位于最上部;随着b增大,危险性曲面逐渐下移,年平均超越概率逐渐降低。与b=5相比,当b=10 时,危险性曲面有所下降,但二者基本重合,这个结论对三种相关系数均成立,并且与Wang 等[18]所得结论一致。文献[18]表明,b的值反映了不同EDP 性能极限状态的相关性,b越大,相关性越弱。以IO 为例,b与失效域的关系如图11所示。由图11可知,随着b增大,极限状态曲线和坐标轴围成的面积越大,则失效域面积越小,当概率地震需求模型相同时所得失效概率越小。因此在基于多维性能极限状态的地震风险分析中,忽略性能极限状态的相关性不利于结构安全。
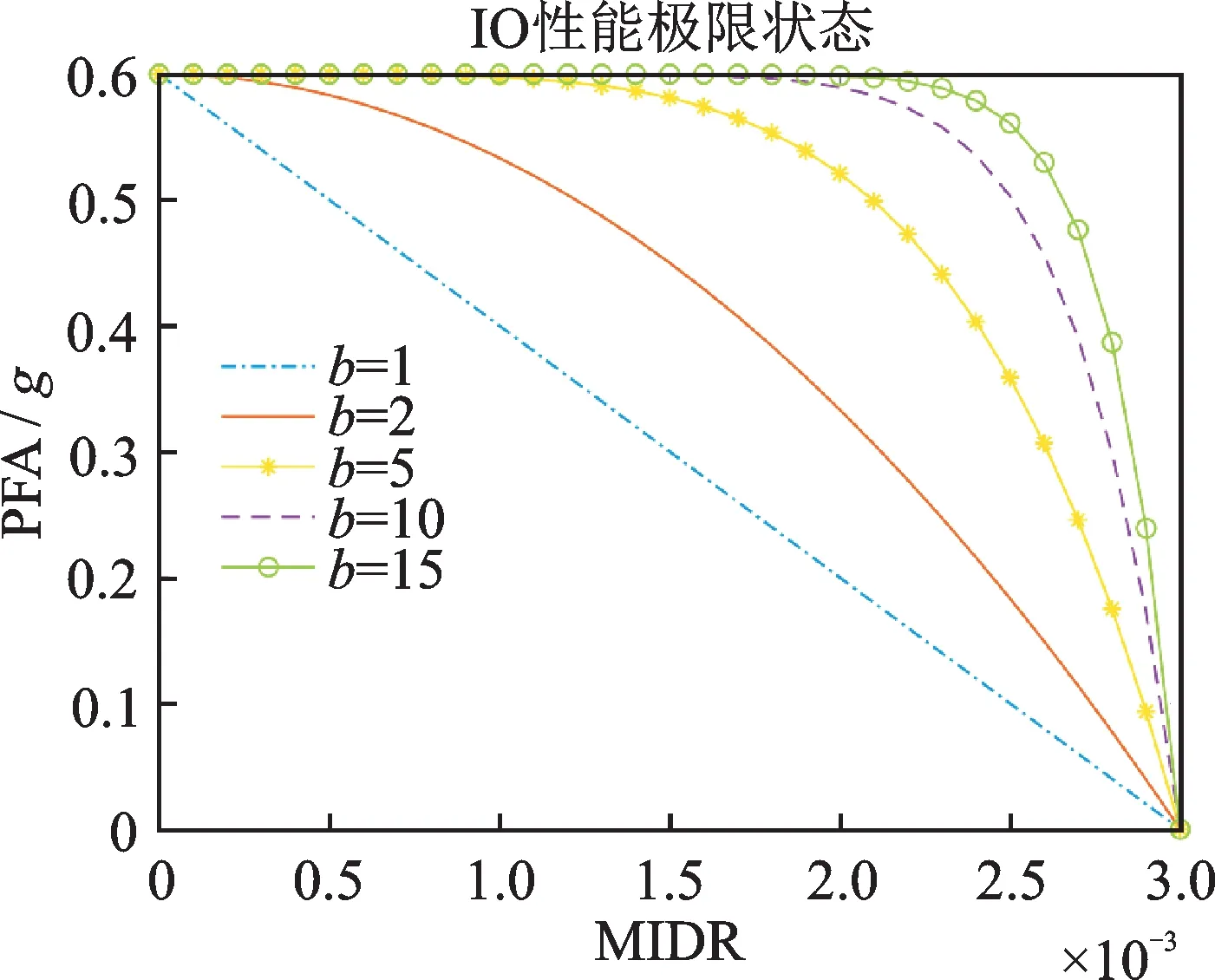
图11 不同b 的极限状态曲线Fig.11 Limit state curves under different b
5 结 论
本文考虑地震激励的不确定性,不对EDP 的分布类型进行人为假定,将传统不考虑相关性的多元核密度估计法拓展到可以考虑随机变量相关性的多元核密度估计用于概率地震需求分析。考虑了三种相关系数,在多维性能极限状态下建立了基于多元相关核密度估计的概率地震需求模型,通过MC 法简化了传统概率地震需求分析的多重积分公式,得到了年平均超越概率,所得结论如下:
(1)与传统基于多维对数正态分布假定的概率地震需求分析相比,相关核密度估计得到的结构需求年平均超越概率偏大,而传统不相关的核密度估计年平均超越概率偏小。一方面说明对数正态分布假定可能会得到不准确的评估结果,另一方面表明EDP 的相关性也会显著影响到年平均超越概率。
(2)在三种相关系数中,Pearson 相关系数得到的年平均超越概率最大,Spearman 相关系数次之,Kendall 相关系数最小。因此不同的相关系数同样会影响到年平均超越概率的大小。
(3)在二维性能极限状态方程中,b越大,EDP性能极限状态相关性越弱,当采用相同的相关系数建立概率地震需求模型后,所得年平均超越概率越小。因此忽略性能极限状态的相关性会导致地震需求概率偏低,不利于工程安全。
由于不同的相关系数会影响到多元核密度估计的结果,研究人员可根据实际情况选择合适的相关系数,利用本文提出的地震需求概率分析方法得到结构需求在设计年限内的平均超越概率。

