绝对节点坐标法中压电层合板的大变形研究
郭永彬,孙靖尧,黎 亮,章定国
(南京理工大学理学院,江苏 南京 210094)
1 概 述
压电材料是一种同时具备正逆压电效应的智能材料,可被用作传感器和作动器,并被广泛用于振动控制、压电驱动、健康监测、能量收集等领域。由于近年来对轻型结构的需求不断增多,在上述的应用中,特别是压电驱动方面,包含大变形的压电层合结构具有越来越重要的研究价值。当结构的表面被压电复合材料覆盖并且施加外部电压到作动器时,可折叠的智能结构(例如折纸结构和软体机器人)可以变形到所需的形状。
目前,已有大量论文进行过包含压电材料的结构的非线性分析[1-6],这些研究工作主要关注传统的压电陶瓷。实际上,压电陶瓷通常具有较高的结构刚度,这使其在粘结过程中(尤其是在粘贴弯曲表面上时)易于损坏。而压电纤维基复合材料不仅具有柔韧性,还具有很高的驱动力,因此受到了研究人员的关注。即使经历大的变形,压电复合材料仍可以紧密地贴合基层的表面。郭翔鹰等[7]研究了压电纤维复合材料(MFC)层合壳的非线性动力学问题。研究人员还证实,使用基于压电纤维的复合材料(如PVDF 和MFC)在结构振动抑制方面的性能要优于传统的压电陶瓷[7-8]。上述工作采用的理论均是基于小变形假设,因此并不适用于研究结构的大变形问题。
绝对节点坐标法(ANCF 法)由Shabana 等建立[9-10],与假设模态法以及传统有限元法相比,ANCF法更适合柔性系统大变形建模。在过去的20年中,大量学者尝试了不同的新单元来描述更为复杂的机械模型[11]或解决早期研究中出现的诸如泊松锁定和剪切锁定等问题[12],并提高计算的精度[13]。ANCF法具有常质量矩阵,零离心力和科氏力等特点,并且可以精确描述刚体的运动[14]。唯一形式复杂的部分是刚度阵,它是由连续介质力学或弹性线方法推导出的[15]。随着ANCF 的广泛应用,该方法也可用于创建更精确的模型来分析复合结构的力学特性。张炜华等[16]对大变形复合材料薄板的多体系统动力学建模方法进行了研究。游斌弟等[17]进行了空间望远镜层合材料镜片展开过程非线性动力学行为分析。目前对于层合结构的位移场,主要有两种描述方法:等效单层(ESL)模型和分层模型[18]。在ESL 模型中,层合结构的变形将被视为与单层结构相同。不同层的运动和变形都使用相同的自由度,该自由度一般在多层结构的中间轴上。这种建模方法的优点是,沿厚度方向的位移场是平滑的,并且无需层与层之间的边界条件,因此计算效率大为提高[19]。在分层模型中,位移场在每个层中都是平滑的,但在层的界面处不是平滑的。ESL 模型和分层模型的示意图如图1所示。使用分层模型得到的结果一般更准确,但由于自由度过多,会影响计算效率。

图1 层合结构模型Fig.1 The model of laminated structures
基于ANCF 法的ESL 模型也可用于小变形或大变形的压电层合结构。Gilardi 等[20]基于ANCF法建立了压电作动器覆盖的柔性梁模型,研究了其静态和动态特性,并优化了高速旋转下的振动控制效果。Jiang 等[21]基于高阶位移场,二次电势场和线性温度场建立了压电层合板结构的数学模型,并提供了数值模拟计算。Liu 等[22]提出了一种新的计算方法用于由层合板组成的大型刚柔多体系统的动态分析。文献[23-24]基于ANCF 法建立了多层压电薄板单元模型,并分析了由压电作动器驱动的三层薄板结构的振动特性。将计算的数值结果与商业有限元软件COMSOL 的仿真结果进行对比,结论较为一致。但是文献[23-24]在推导过程的弹性力项中忽略了拉伸项应变,这使得该单元只能用于低张力板;同时,其建立的层合板离散模型使用的单元数量较少,有可能会在横向变形更大的情况下达不到计算精度要求。易灿明等[25]基于绝对节点坐标法,通过变形协调条件,建立了以基层为薄板单元,压电层为梁单元的梁板耦合模型。
本文采用ANCF 法,在文献[23-24]的基础上建立了一种考虑板的拉伸项应变的压电层合薄板单元,推导了该单元的动力学方程,并进行了几组静力学和动力学仿真。结论指出,压电层合薄板单元也可以很好地和线弹性单元耦合,即可以表达压电材料覆盖在层合薄板上任意位置的情况。
2 动力学模型
2.1 缩减板单元
在绝对节点坐标法中,节点坐标将定义在全局坐标系中。对于层合薄板单元,全局坐标将存在于三维空间中。如图2所示,板单元中面上任意一点P的位置矢量r在全局坐标中描述为:

图2 层合薄板单元模型Fig.2 The model of thin laminated plate
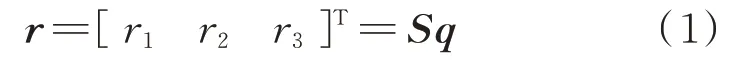
式中r1,r2和r3分别为全局位置矢量r的三个分量;S为单元的形函数,具体形式为:

其中:
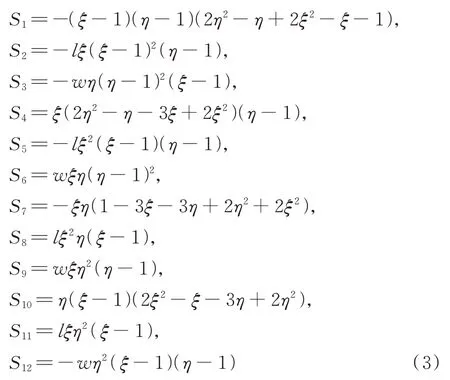
式中l和w分别代表未变形状态下板单元的长度和宽度;I3×3是一个大小为3×3 的单位矩阵。ξ=x/l,η=y/w。x和y分别代表板单元未变形时中面上任意一点P在板单元坐标系下沿长度方向和宽度方向的坐标。
对于四节点缩减板单元,每个绝对坐标应包含9 个自由度,分别为:
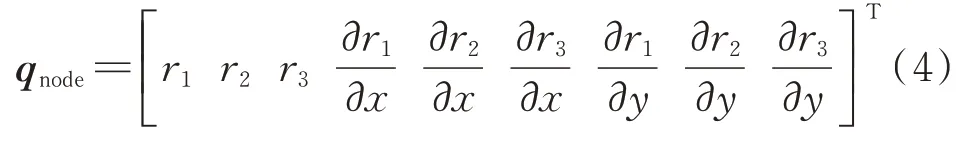
这样每个单元应包含36 个自由度。
2.2 等效单层模型
在对层合单元的积分过程中,需要分成三个部分来逐层积分。假设板单元长度为l,宽度为w,基层厚度为hp,压电作动器厚度为ha,压电传感器厚度为hs,则:
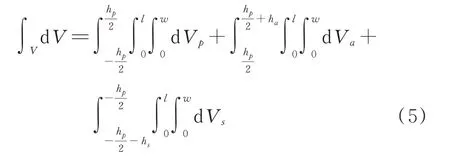
式中Vp,Va和Vs分别为板单元中基层、压电作动器和压电传感器的单元体积。
如果是单层板单元,则只需要公式(5)中的第一项,即:
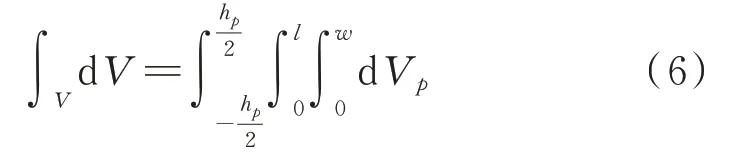
2.3 压电材料的本构方程
在三维空间中,如果压电材料仅在z轴方向产生极化效应,那么压电材料的本构方程将表示为:
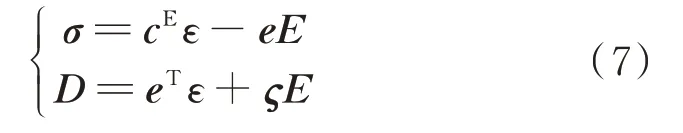
式中σ表示应力矢量;ε表示应变矢量;cE表示弹性矩阵;E表示电场强度;D表示电位移;e表示压电常数矩阵;ς表示介电常数矩阵。
各分量写成矩阵或向量形式为:
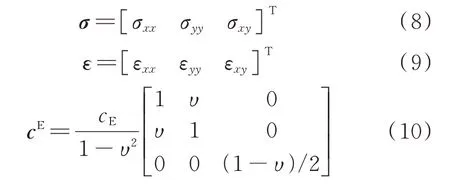
式中υ和cE分别代表压电材料的泊松比和弹性模量。

对于基层的线弹性材料,可以将本构方程中的压电常数矩阵和介电常数矩阵均视为0 矩阵,则可退化为线弹性材料的本构方程,即:
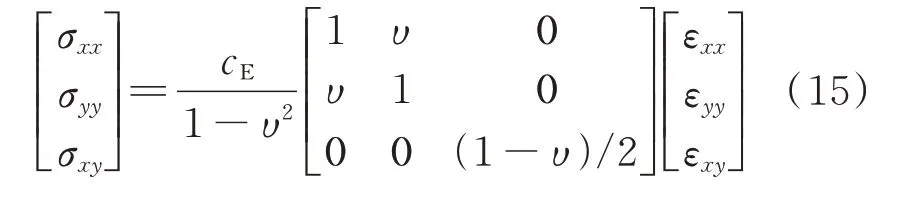
另外,需要注意的是,当基层弯曲时,覆盖在顶层的压电传感器中的电荷将在内部移动,从而导致压电传感器的上端和下端的电荷分布不均匀,传感器将收集此电压信号作为反馈。同时,如果对作动器施加电压则会导致基层弯曲。压电层中的电压和电场强度之间的关系为:
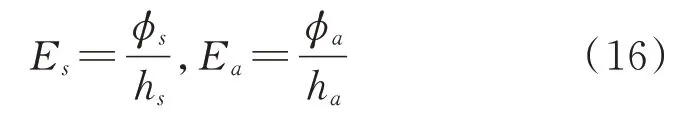
式中ϕs和ϕa分别代表传感器和作动器的电压;Es和Ea分别表示传感器和作动器的电场强度。
2.4 广义质量阵
将公式(1)对时间求导,可以得到:

层合板单元的动能表示为:
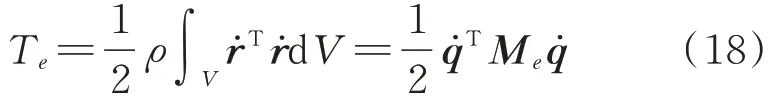
其中,单元质量阵可由动能导出:
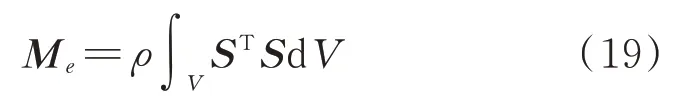
式中ρ为板单元的等效密度。
2.5 广义弹性力
层合板单元的弹性势能为:
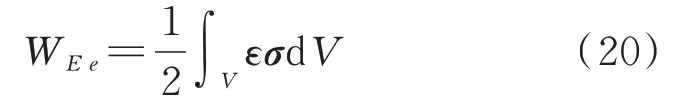
将压电材料的本构方程代入公式(20)可得:
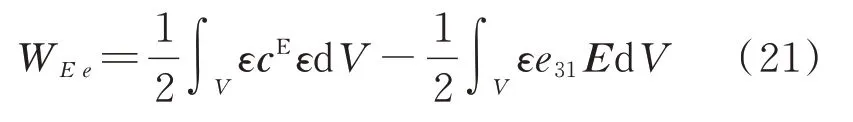
将公式(21)对广义坐标q求导后可得:
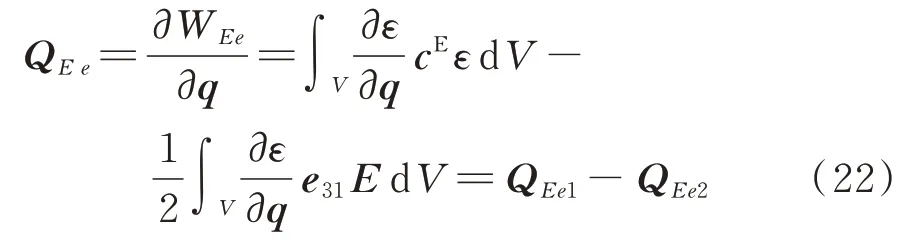
其中
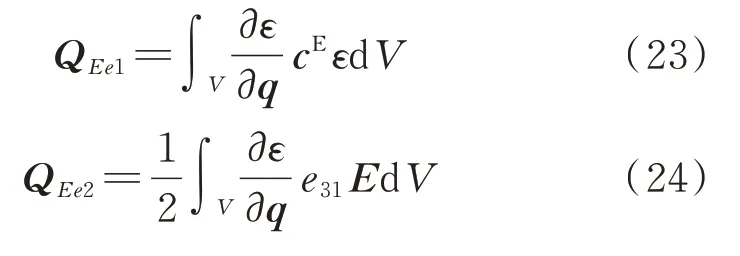
根据连续介质力学,应变表示为:

其中,拉伸方向的应变εm由拉格朗日应变张量导出:

分别将εm对绝对节点坐标求一次和二次偏导,可以得到下式:
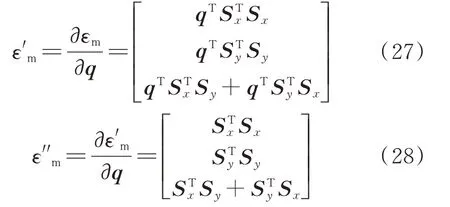
弯曲方向的应变由曲率的定义式导出,其中精确的曲率公式为:
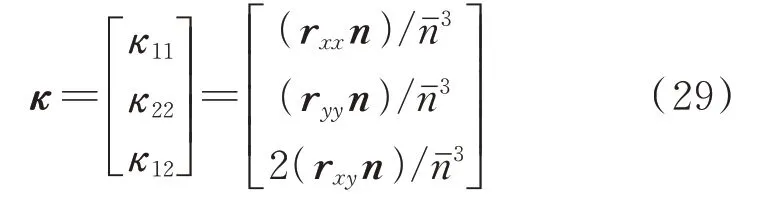
为了简化计算,曲率可以简化为以下形式,本文中称之为一次简化公式:
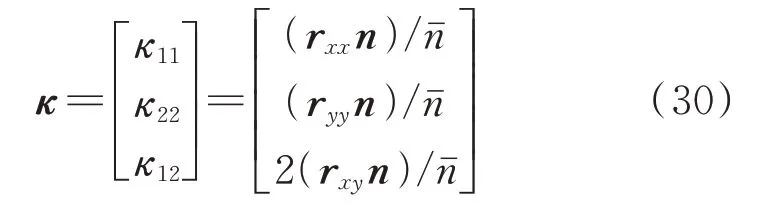
或者简化为曲率和绝对节点坐标之间的线性关系,本文中称之为线性简化公式:
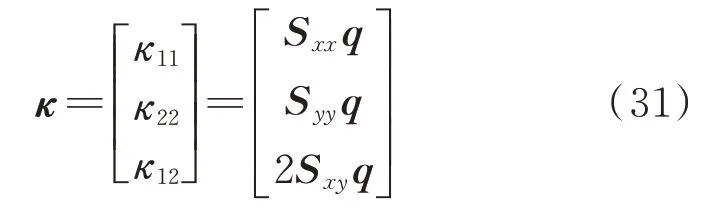
接下来以精确的曲率公式为例进行推导,其他的形式同理。在公式(29)中,有:
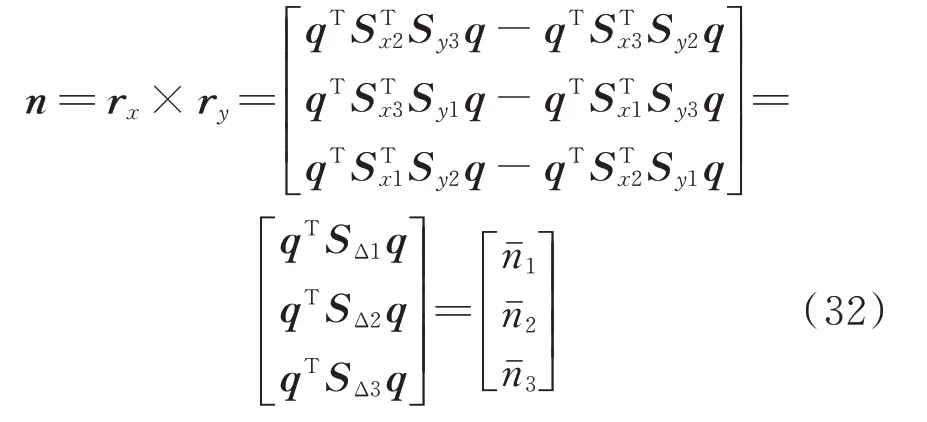
以及

其中

将n对绝对节点坐标求一次和二次偏导,可得:

将对绝对节点坐标求一次和二次偏导,可得:
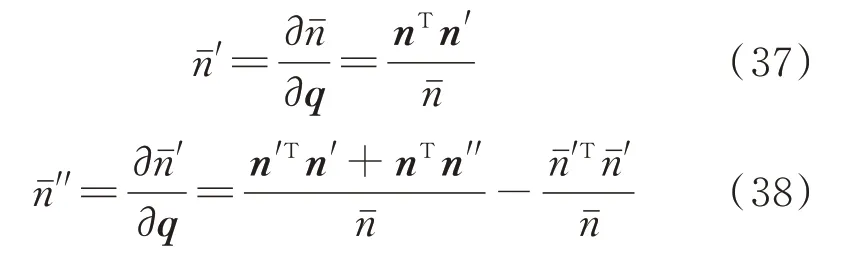
曲率κ对绝对节点坐标求一次偏导为:
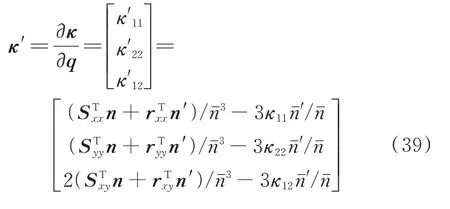
将公式(26)~(39)代入(23)和(24)可以得到:
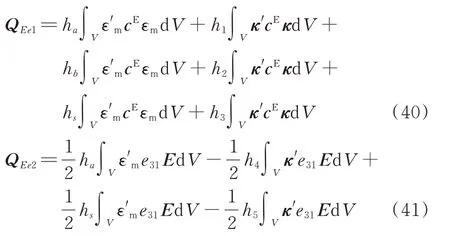
其中,公式(41)还可以进一步化简为:
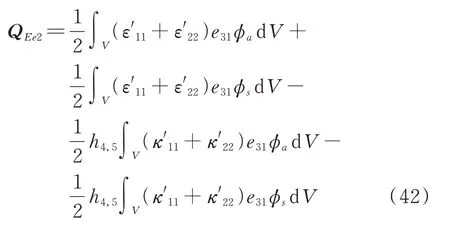
推导过程中一些与结构横截面几何形状有关的常数如下:
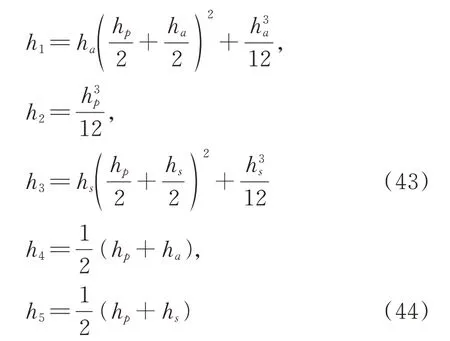
式中 下标p,a和s分别代表基层,作动器层和传感器层。
2.6 广义压电力
在压电层合单元中,电势能为:
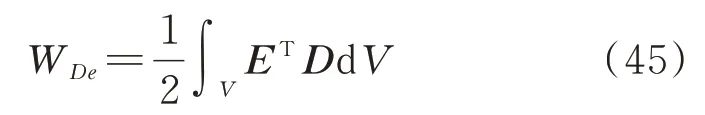
将本构方程代入公式(45)可得:
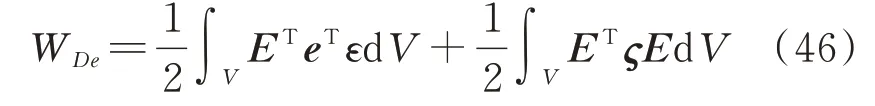
将电势能分别对传感器层电压ϕs和作动器层电压ϕa求导,可以得到广义压电力:
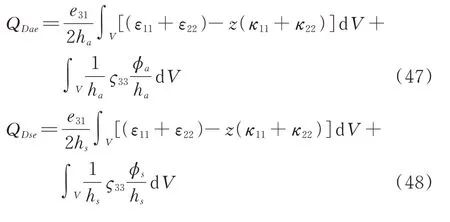
如果不考虑外界在作动器上输入的电压,则有QDse=0 以及QDae=0,这样即可对公式(47)和(48)求解,得出由结构变形引起的压电材料上下端的电势差。
2.7 动力学方程
在求得单元内的上述各项之后,需要对每个单元进行组装。
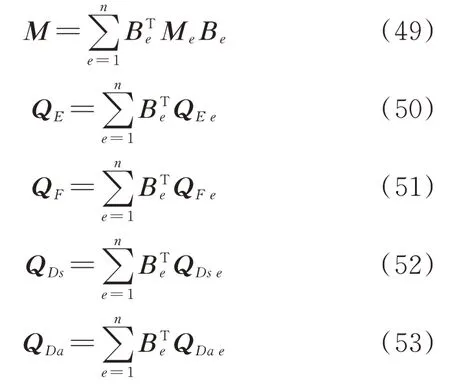
式中Be表示薄板单元节点坐标向量对应总体绝对节点坐标列阵中的布尔定位矩阵;M表示整体质量矩阵;QE表示板的整体广义弹性力向量;QF表示整体广义外力向量;QDs表示传感器层的整体广义压电力;QDa表示作动器层的整体广义压电力。
组装后则得到整体结构的动力学方程如下:
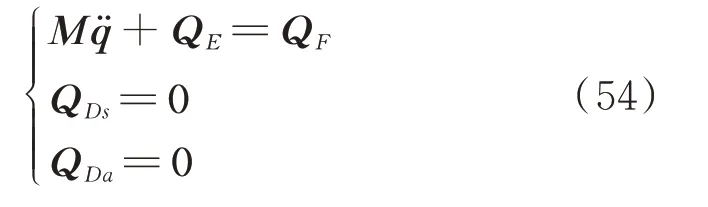
如果求解静力学问题,则动力学方程中将不包含这一项。
3 仿真算例
3.1 不同曲率计算形式的收敛性分析
在进行压电层合结构的相关仿真之前,有必要先明确在大变形范围内三种不同的曲率表达形式的适用性。如图3所示层合悬臂板,长度l=0.5 m,宽度w=0.15 m,厚度分别为中层0.4 mm,上下层各0.3 mm。所有层均为相同的线弹性材料,弹性模量E=207 GPa,泊松比为0.3。板的两个端部分别受到两个大小为F=15 N 的集中力外载荷。分别取单元数为1~48 个的情况,求解出集中力施加位置处薄板的横向位移,研究三种不同的曲率表达形式下各自的收敛性,其结果如图4所示。同时与商业有限元软件ABAQUS 的结论进行对比,ABAQUS 仿真中网格尺寸划分大小为0.005 m,仿真结果显示板的末端横向位移为−0.2868 m,结果如图5所示。
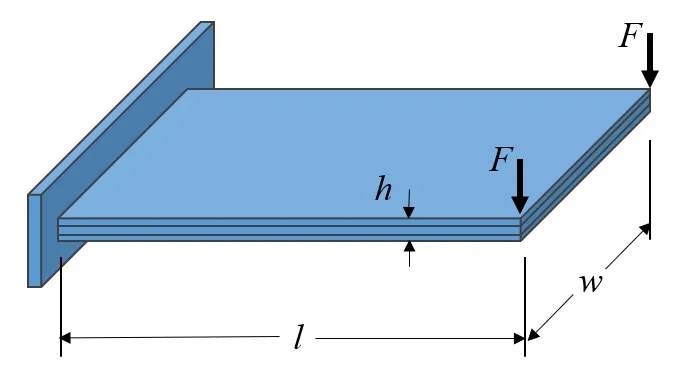
图3 三层线弹性板模型Fig.3 Model of three-layer linear elastic laminated plate
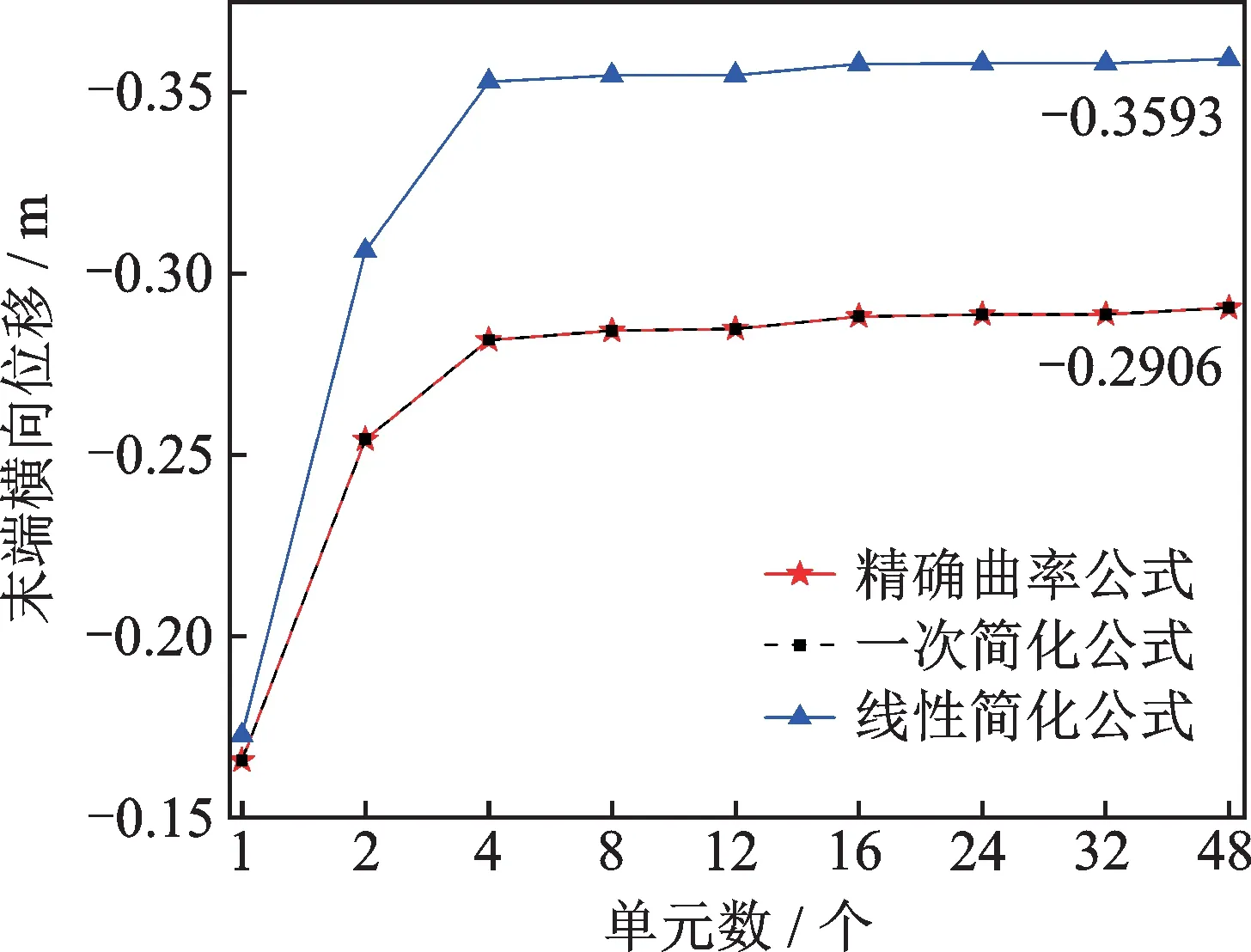
图4 三种曲率计算公式在大变形状态下各自的收敛性Fig.4 Convergence using three different forms of curvature in large deformation

图5 ABAQUS 中的薄板位形图Fig.5 The configuration of the plate in ABAQUS
从图4中可以看出,使用精确的曲率公式和分母简化为一次项的公式得出了一致的结果,而且都可以很好的收敛,并且该结论与ABAQUS 得到的结论几乎相同,相对误差为1.3%。在单元数量为48 个的情况下,使用精确的曲率公式仿真用时为67.54 s,使用分母简化为一次项的公式仿真用时为65.23 s,在相同的计算结果下计算效率有小幅度的提升。使用线性简化形式的曲率公式,虽然结果可以收敛,但产生的横向变形相比于真实值明显偏大。由此可见,线性简化公式是难以在大变形的条件下使用的。
3.2 薄板在集中力作用下产生大变形
算例2 验证了压电层合薄板模型在不同大小的外力作用下的正确性。如图6所示的三层悬臂板,长度l=0.6 m,宽度w=0.4 m,上下两层完整铺设厚度为0.5 mm 的压电材料,中间层为1 mm 厚的线弹性材料。线弹性材料的弹性模量为73 GPa,泊松比为0.3;压电材料的弹性模量为107 GPa,泊松比为0.3,压电常数为−6.5 C/m2,介电常数为3.01×10−8F/m。离散单元为沿长度方向6 个单元,沿宽度方向4 个单元,共24 个单元。本文所有算例中的单元编号规则均与图6中所示相同。在悬臂板末端一角施加一个沿z方向的集中力,其大小与该点横向位移的关系如图7所示。
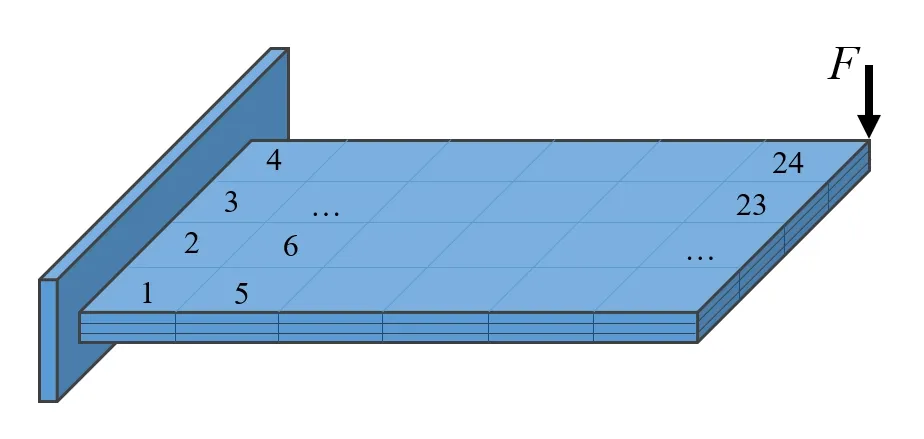
图6 全覆盖的压电层合板模型Fig.6 Laminated plate with fully covered piezoelectric patches
从图7中可以看出,使用线性简化的曲率公式得到的位移也是线性变化的。在不超过30 N 的范围内,使用线性简化的曲率可以和精确曲率的方法得出近乎一致的结果,且相对误差不会超过1%。但随着集中力的增大,使用线性简化的曲率计算出的结果会逐渐偏离理论值。
3.3 薄板在作动器施加电压情况下产生变形
算例3 验证了压电层合薄板模型在外电压作用下的正确性,同时探索了部分覆盖压电材料的情况下该单元与普通线弹性材料单元耦合的可行性。基层板的尺寸和算例2 中相同,仅第6,7 个单元是压电层合单元,其余均为单层线弹性材料。材料参数与算例2 相同。在两个覆盖压电材料的单元的作动器上施加逐渐增大的电压,计算板上节点13 和35 的横向位移(如图8所示),其对比结果如表1和表2所示。
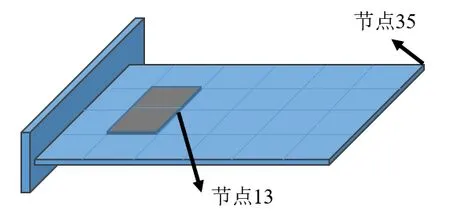
图8 部分覆盖的压电层合板模型Fig.8 Laminated plate with partly covered piezoelectric patches

表1 不同电压下节点13 的横向位移Tab.1 Displacement of the 13th node in different voltages

表2 不同电压下节点35 的横向位移Tab.2 Displacement of the 35th node in different voltages
接下来讨论压电层合单元在上下两侧均覆盖作动器的情况,基层和压电材料厚度均为1 mm。层合薄板结构在沿长度方向的0.1~0.3 m,沿宽度方向的0~0.4 m 处覆盖压电材料。基层线弹性材料的弹性模量E=0.49 GPa,泊松比为0.33;压电材料的弹性模量E=39.6 GPa,泊松比为0.33,压电常数为−6.948 C/m2,介电常数为3.01×10−8F/m。考虑到压电作动的情况下随着变形量数量级的增大,需要更多的单元数量才能接近收敛值,此处离散单元数量为沿长度方向24 个,沿宽度方向12 个,共288 个单元。在作动器施加0~1000 V 逐渐增大的电压,求解出薄板自由端角落位置(即图9中A 位置)的横向位移如图10所示。可以看到,在施加电压的情况下,变形趋势也与施加集中力的情况相同,呈现一种非线性趋势。
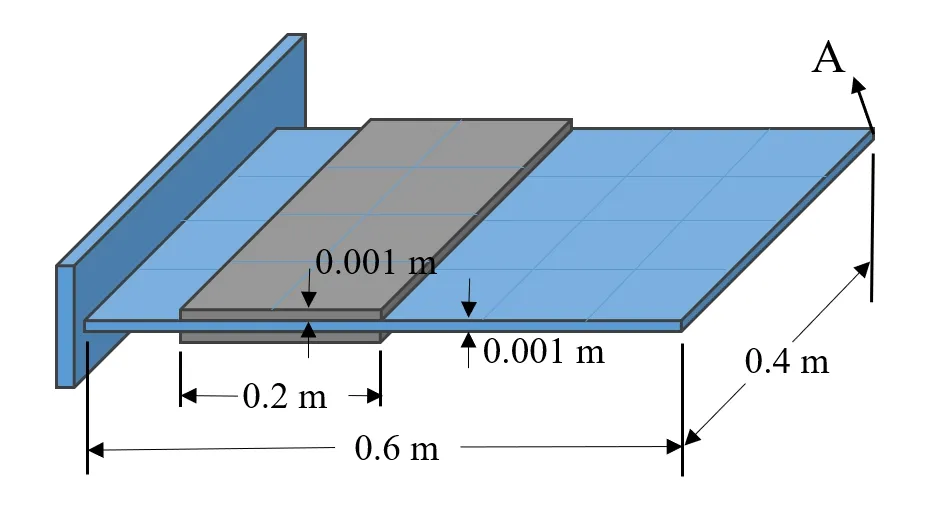
图9 双侧部分覆盖的压电层合板模型Fig.9 Laminated plate with segmented piezoelectric patches on two sides
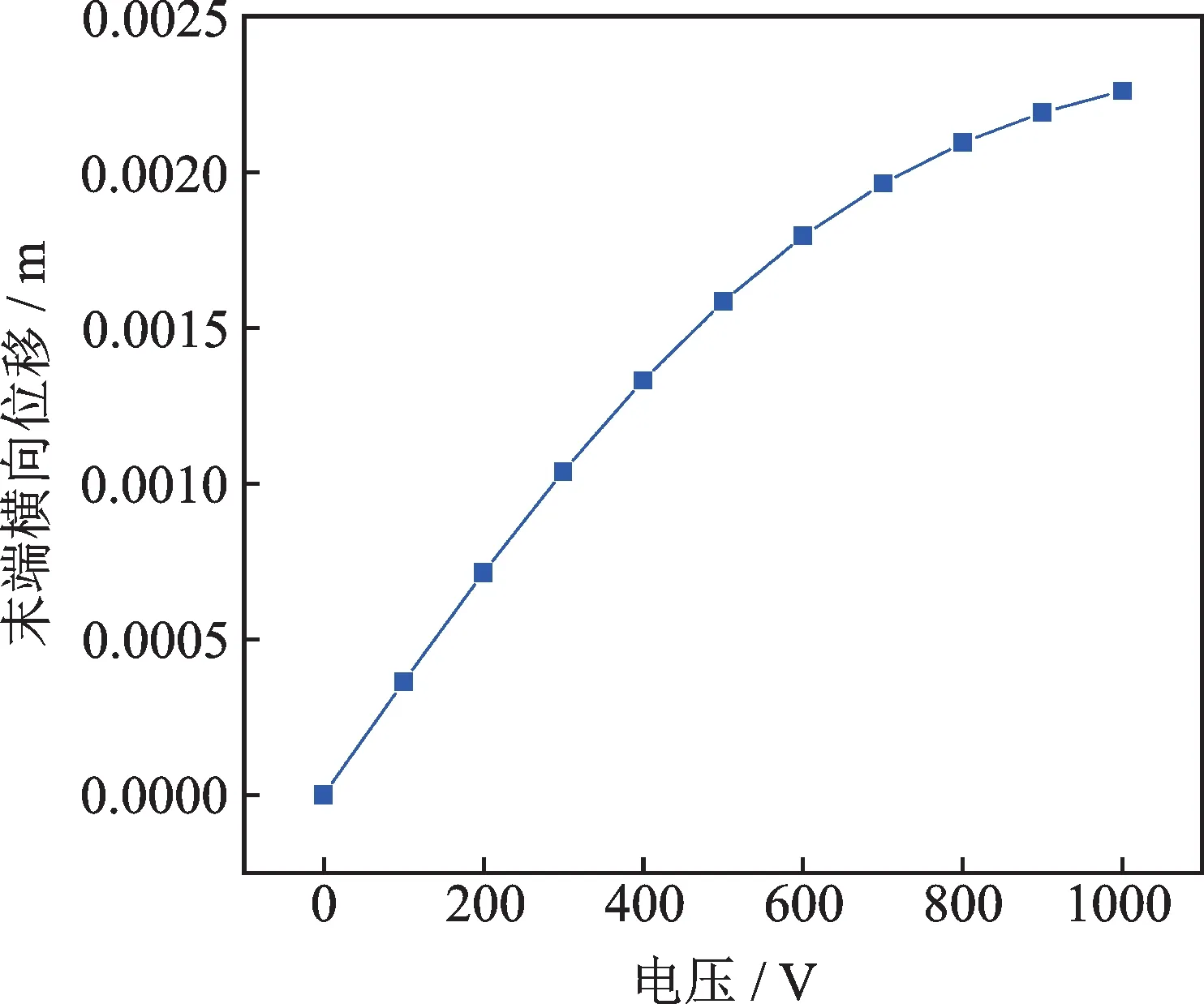
图10 不同电压下薄板末端的横向位移Fig.10 The tip displacement in different voltages
最后计算一组分段贴片的情况。层合薄板结构在沿长度方向的0.1~0.2 m,以及0.4~0.5 m 处分别覆盖一组压电材料,一侧为传感器层,一侧为作动器层,施加电压为500 V,模型如图11所示。基层线弹性材料的弹性模量E=0.49 GPa,泊松比为0.33;压电材料的弹性模量E=3.96 GPa,泊松比为0.33,压电常数为−6.948 C/m2,介电常数为3.01×10−8F/m。离散单元同样取288 个。变形后基层线弹性材料薄板部分的三维位形图如图12所示。
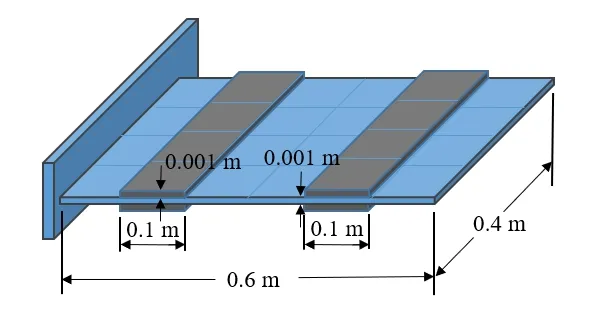
图11 分段覆盖的压电层合板模型Fig.11 Laminated plate with multiple piezoelectric patches

图12 施加500 V 电压下层合板的位形图Fig.12 The configuration of laminated plate under 500 V
从图12中可以看出,层合薄板在受到电压驱动的状态下,变形方式并非简单地围绕y轴方向进行卷曲,而是朝向类似球形的趋势产生变形,导致矩形的薄板在电压作用下远端的角落处变形比中间处更大,而在薄板中心位置有一处明显的凹陷。
3.4 压电层合板动力学仿真
对算例4 进行动力学仿真。压电层合薄板的压电材料为全覆盖,线弹性材料和压电材料参数与算例1 相同。离散单元数量为沿x轴12 个,沿y轴8个,共96 个单元。仿真时间为1 s,求解出仿真时间内集中力处的横向位移随时间的变化如图13所示。第1 单元,第44 单元和第96 单元的电压随时间的变化如图14所示。

图13 压电层合板在集中力作用下的位移随时间变化情况Fig.13 The displacement of piezoelectric laminated plates varies with time under the concentrated force
通过图13和14 可以看出,在越靠近约束端的位置,集中力作用下产生的电压越大,而在施加集中力的自由端电压值反而较小。电压的增减趋势与横向位移的变化具有大致相同的周期。
4 结 论
本文基于绝对节点坐标法建立了一个压电层合薄板单元,并通过几组算例验证了单元的正确性,以及使用不同形式的曲率计算公式下的收敛性。在大变形范围内,线性的曲率计算方法将不再适用,其计算结果相比于真实值偏大。当电压施加到压电板单元中的作动器时,层合薄板将弯曲,其值与ABAQUS 有限元软件提供结果基本一致,这表明本模型描述压电耦合效应时具有很好的实用性,且在压电材料全覆盖或是部分、分段覆盖的情况下皆可适用。

