开关磁阻直线电机的设计及其推力优化
马霁旻,万梓灿,王 杜,万子威
(1. 湖北工业大学,武汉 430068; 2. 智新科技股份有限公司,武汉 430056)
0 引 言
开关磁阻电机(以下简称SRM)是一种双凸极结构电机,其在转子位置不包含磁钢及线圈,结构较简单,可靠性较强,可应用于纺织行业及伺服驱动系统。开关磁阻直线电机(以下简称LSRM)是由旋转式开关磁阻电机沿径向展开形成,是其一种结构上的延伸。开关磁阻直线电机继承了传统开关磁阻电机的优点,具有结构简单、容错性能强及控制灵活等特点,并且区分于传统直线电机,它还具有直接将电能转化成机械能的能力,因此,可靠性、精度、系统结构等方面有明显的优势。
JMAG仿真软件是一种功能齐全、应用广泛的电磁场分析软件。JMAG相较于其它有限元分析软件,拥有完善的自学系统,能让新手在短期内迅速掌握,各个分析模块也可在condition界面中拉出,上手十分容易。其外电路部分结构简单,便于控制,因此可用于开关磁阻电机的仿真。
有取向硅钢得益于它的内部结构中晶粒方向的一致性,因此经常被用在磁路单一的变压器上。从化学成分讲,有取向硅钢的硅含量比无取向硅钢的硅含量要高。本文在使用无取向硅钢的基础上对LSRM进行了结构优化,应用JMAG仿真软件,确定推力最大的结构参数;并将有取向硅钢应用于磁路较为简单的LSRM上,推力有一定提升;在动子齿部开切向槽,降低了推力波动。
1 电机模型及特性分析
LSRM是由旋转SRM沿径向剖开并展平而得,因此继承了旋转SRM的特性。本文选用的是12/8极SRM,当其被剖开展平为LSRM时,它的动子极宽与定子极宽的比值依旧为1.5。为了简化仿真,使用JMAG仿真软件对电机的最小单元模型进行仿真,即3/2极,该电机的最小单元模型示意图如图1所示。

(a) 电机结构图

(b) 电机剖分图
图1(a)为电机结构图,电机主要包含动子、定子及线圈绕组,定子从左至右依次绕A,B,C三相绕组,电机所用无取向硅钢牌号为50CS350,定、动子均采用叠压系数为0.95的0.5 mm硅钢片。图1(b)为电机剖分图,由于电机定子齿、动子齿的磁力线较密集,因此在定子和动子的齿端加密剖分,增加精确度。
1.1 LSRM推力方程
LSRM位移对电感的影响可等效为余弦规律表达式:

(1)
式中:Lsi为电机漏感;Lavg为电机电感平均值;wt为电机齿宽与槽宽之和;x为电机位移量。
电机实际运行情况下电机漏感Lsi较小,可将其视为0,于是式(1)可简化:

(2)
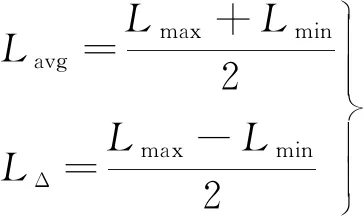
(3)
式中:Lmax为电机最大电感值;Lmin为电机最小电感值。
当一相通入电流时,磁储能Wm可表示:

(4)
式中:i为相电流;Wm为电机等效电感中的磁储能。
当Δx→0时,ΔWm→0。对应的电磁推力:
FΔx=ΔWm
(5)

(6)
当Δx→0时,
1.2 外电路与推力
SRM的运动需要借助外电路的控制,如图2所示,控制电路选用不对称半桥驱动电路。L1、L2、L3依次对应电机中的A,B,C三相绕组,通电次序为在一个电机开关周期中(动子运动一个极距的时间),先只打开S3、S4开关,然后只打开S1、S2开关,最后只打开S5、S6开关,即导通次序为B-A-C,三组开关的导通时间一致,即为按B-A-C的顺序导通。
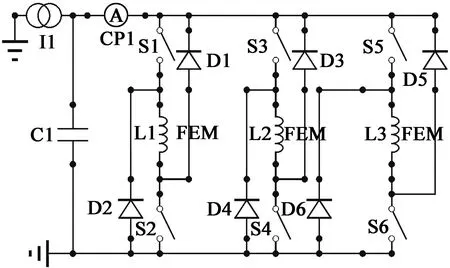
图2 不对称半桥驱动电路
电机选取恒定电流源作为供电电源,通入20 A的直流电,每相匝数为50匝,控制方式为角度位置控制(APC),电机相电流波形如图3所示。
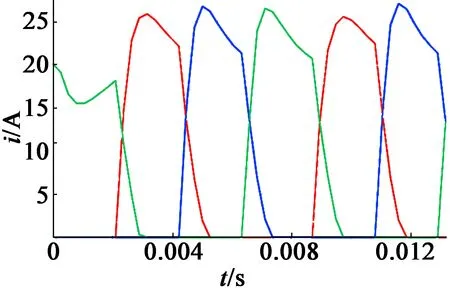
图3 电机相电流波形图
通入20 A直流电后动子运动两个极距的推力波形如图4所示。
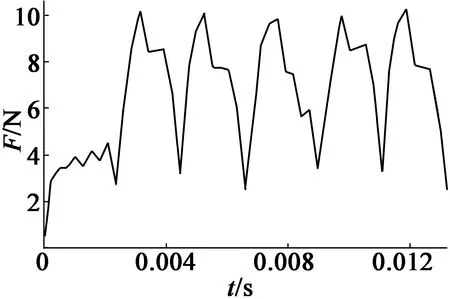
图4 B-A-C三相依次导通时的推力波形图
动子在开始阶段为起动阶段,推力较小,当导通线圈变为A相线圈时,推力逐渐趋于平稳,此后一直以单相导通时间为周期进行推力波动。
1.3 初始位置对推力的影响
改变控制电路的开关时间可以影响推力,而直接改变各相导通时间对推力波动的影响较大,因此选择改变动子的初始位置,相当于间接改变开关时间。开关周期为动子运动一个极距的时间,因此选择推迟一个开关周期进行仿真,即初始位置从-66 mm到0,仿真结果如图5所示。
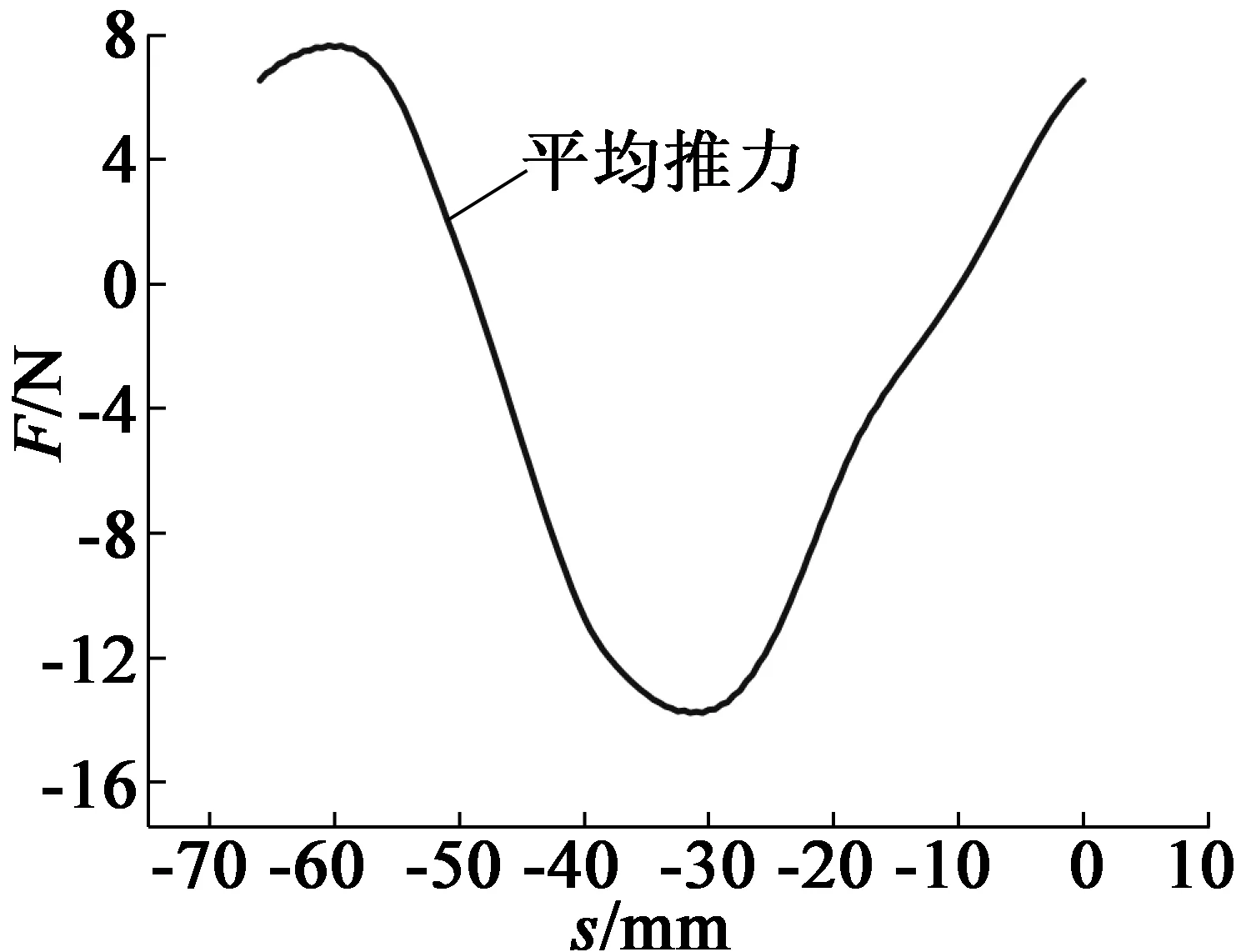
图5 延后一个开关周期的推力变化图
从图5中可以看出,推力随着初始位置的变化,呈现出一个凹形变化,在-60.5 mm处正向推力最大,在-30.5 mm处反向推力最大。
1.4 三种典型位置的磁密矢量图
为探究LSRM的磁力线分布,现对三种典型位置的磁力线进行仿真分析。
图6为B相结束导通时的磁力线矢量图。当B相结束导通时,动子齿和定子齿还未完全重合,此时仅由B相提供推力,电机还处在起动阶段,最大磁密仅有1.35 T。
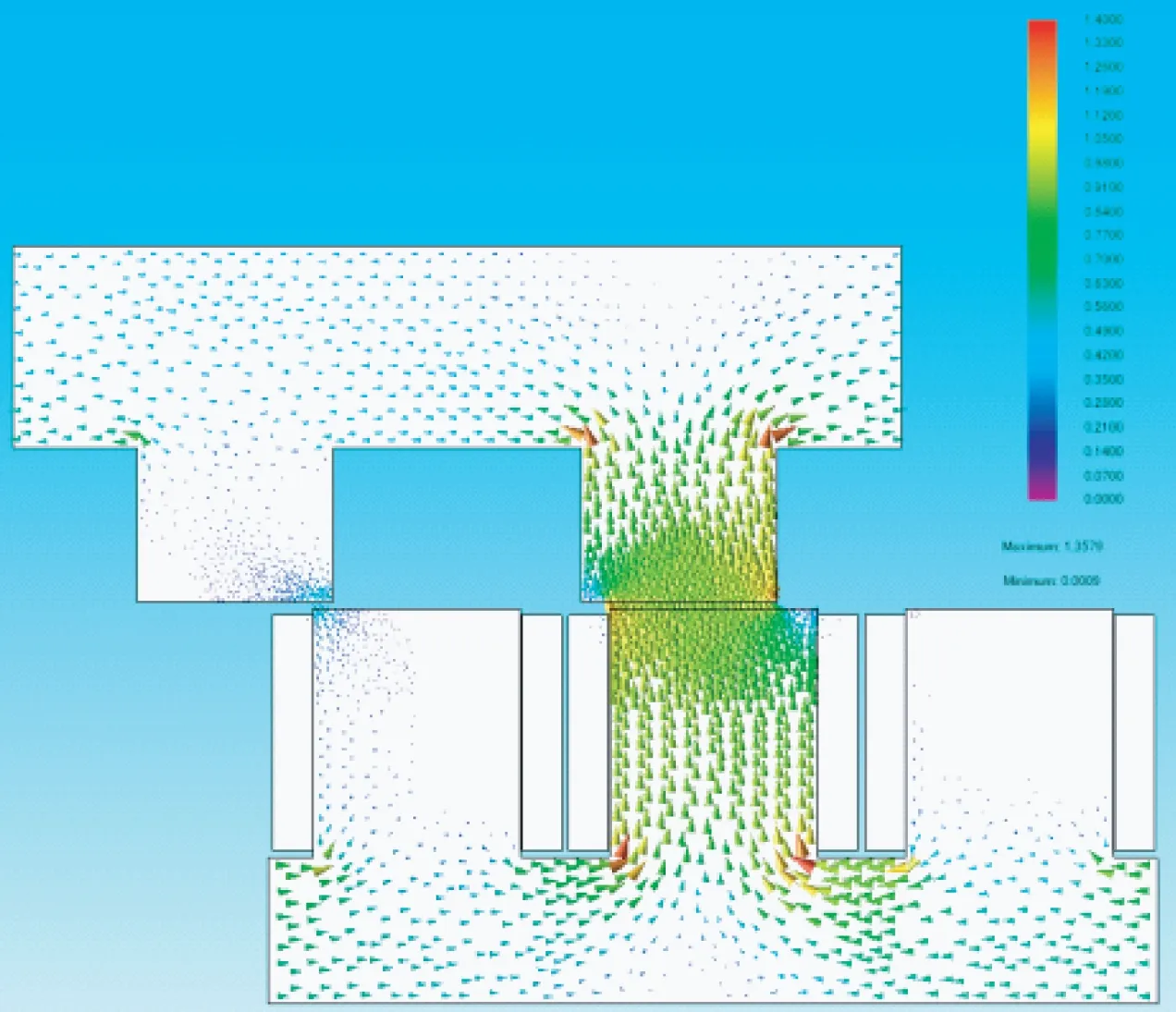
图6 B相结束导通的磁力线矢量图
图7为A相开始导通的磁力线矢量图。此时电机已达到额定速度,由A相提供推力,此时A相最大磁密已达到1.86 T,电机处于稳态运行状态。
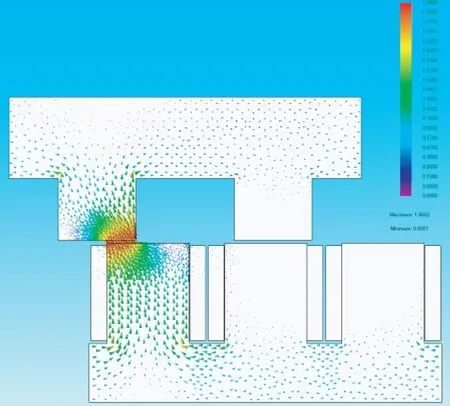
图7 A相开始导通的磁力线矢量图
图8为A相切换C相导通的磁力线矢量图。此时,推力由A相和C相共同提供,A相齿与动子齿完全对齐,C相与动子齿也处于半对齐状态,此时最大磁密仅为1.41 T,这也导致了换相时的推力波动。
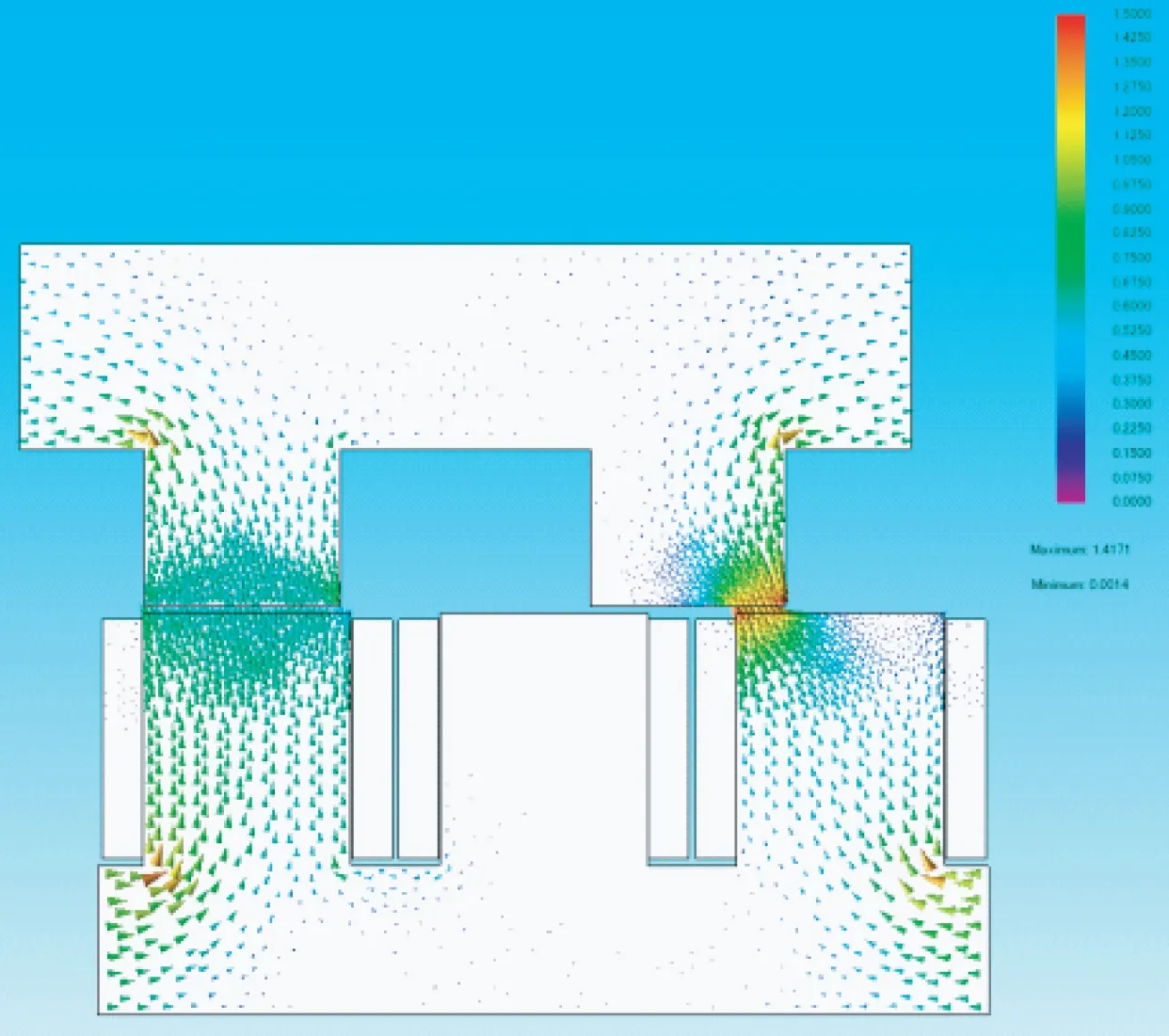
图8 A相切换C相导通的磁力线矢量图
2 采用无取向硅钢的电机结构优化
电机定子、动子结构如图9所示,主要结构参数均标注于图9中。

图9 电机结构示意图
2.1 电机结构优化
通过定子、动子齿的磁力线对LSRM推力影响较大,定子、动子齿宽的变化对磁路影响较大,进而影响推力的大小,而单个变量仿真精确度不够,无法寻找到最优点,因此对定子极宽比σs、动子极宽比σr进行双变量仿真,研究其对平均推力的影响。定子、动子极宽比取0.3~0.7,仿真结果如图10所示。
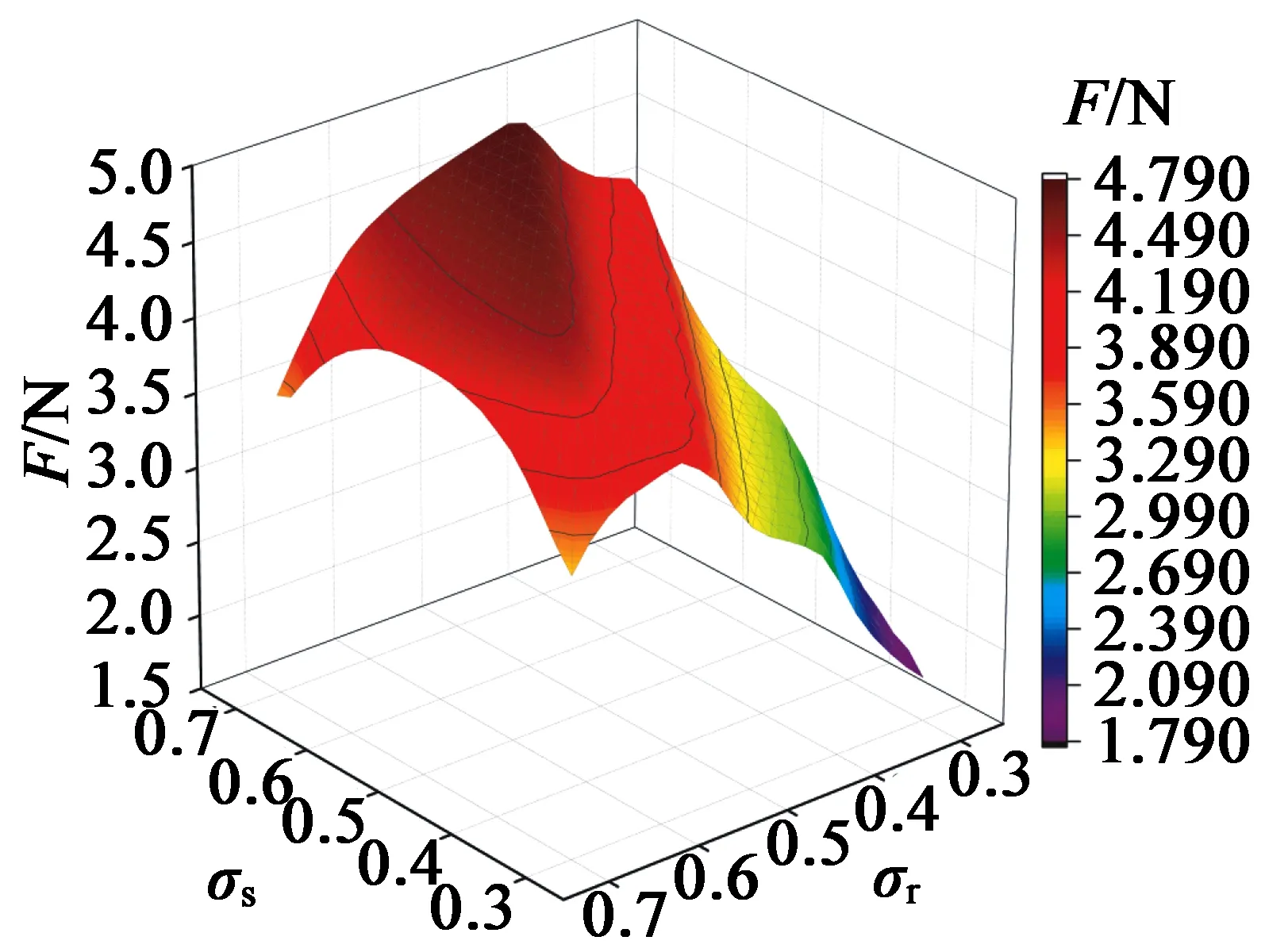
图10 不同定子极宽比、动子极宽比下的平均推力曲线
由图10可知,当动子极宽比一致时,平均推力随着定子极宽比的增加而近似线性增加;而当定子极宽比一致时,平均推力随着动子极宽比的增加而呈一个先增后减的趋势,并在动子极宽比为0.44左右达到最大。
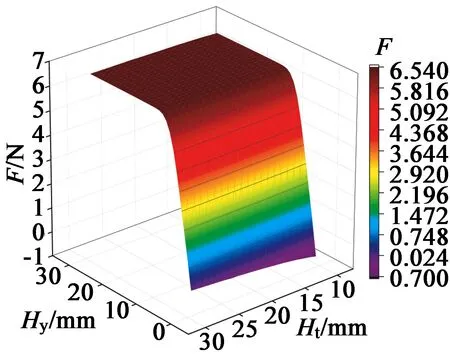
图11 不同动子齿部高度、轭部高度下的平均推力曲线
图11显示了不同动子齿部高度、轭部高度下的平均推力曲线。由图11可知:当动子齿部高度Ht一致时,随着动子轭部高度Hy的增加,平均推力先线性增加,当动子轭部高度达到10 mm以上时,平均推力趋于稳定;当动子轭部高度一致时,随着动子齿部高度的增加,平均推力缓慢增加。
由于改变齿部高度、轭部高度会对铁耗有较大影响,因此对不同齿部高度、轭部高度下的动子铁耗进行研究,如图12所示。

图12 不同动子齿、轭部高度下的动子铁耗曲线
由图12可知,当动子齿部高度Ht一致时,随着动子轭部高度Hy的增加,铁耗呈现一个先增后减的趋势,并在动子轭部高度9 mm处达到最大,由于轭部高度小于9 mm时,动子轭部始终处于饱和状态,铁耗也随着轭部高度的增加而线性增加,而当轭部高度大于9 mm,轭部逐渐趋于非饱和状态,因此铁耗逐步降低。动子轭部高度一致时,随着动子齿部高度的增加,铁耗也会逐渐增加,但当轭部高度大于9 mm后,相同齿部高度的铁耗会逐渐降低。
由于定子槽满率的要求,不对定子齿部高度进行分析,仅对定子轭部高度进行研究,如图13所示。
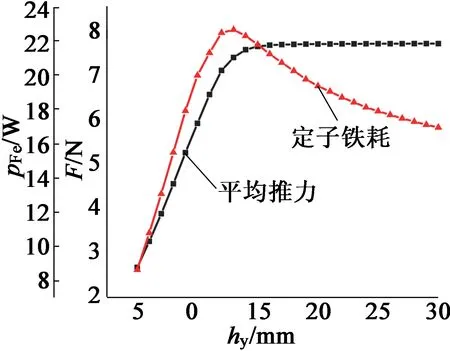
图13 不同定子轭部高度下的平均推力与铁耗变化曲线
由图13可知,随着定子轭部高度的增加,推力呈线性增加趋势,直到高度达到16 mm,推力趋于平稳,而定子铁耗则在13 mm处达到了最大值,此后随着定子轭部高度的增加而逐渐降低,定子轭部由饱和状态变为不饱和状态。
2.2 电机主要尺寸参数
综合考虑硅钢片用量、平均推力、铁耗的要求,确定了电机主要尺寸如表1所示。
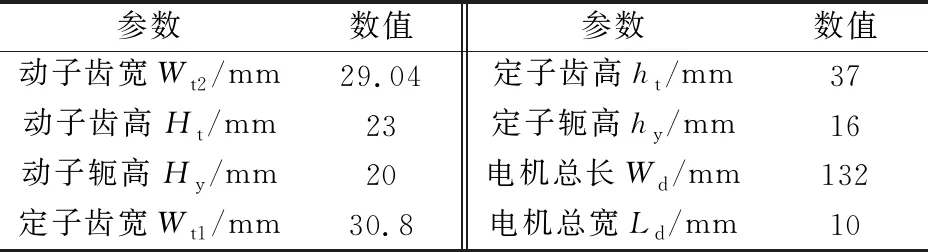
表1 电机主要尺寸参数
3 采用有取向硅钢的电机结构优化
有取向硅钢在轧制方向上磁导率较高,而在垂直于轧制方向上的磁导率较低,甚至低于普通无取向硅钢材料,铁耗特性也较差,因此,有取向硅钢材料适用于磁路较为简单的场合,如变压器等。LSRM磁路简单,因此可选武钢牌号为35Q145的有取向硅钢应用于该电机,电机结构如图14所示。
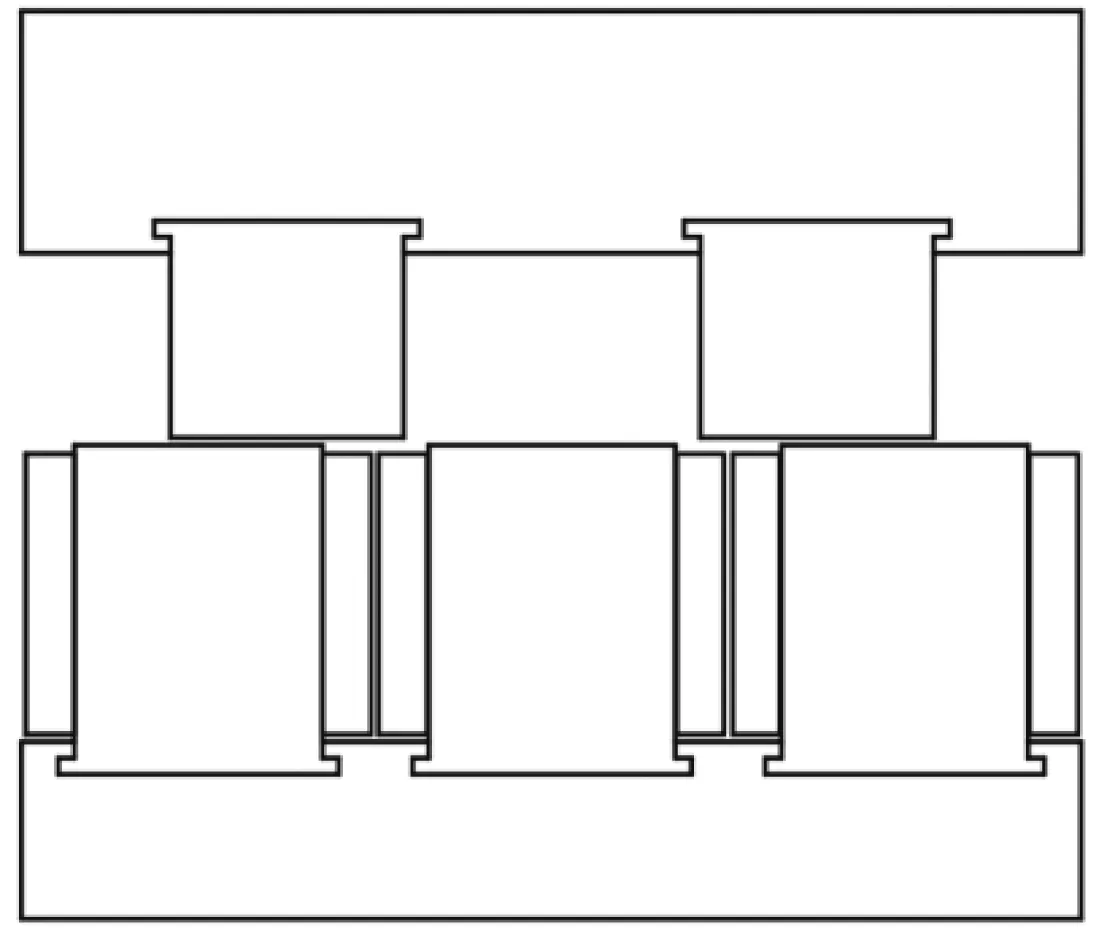
图14 基于有取向硅钢的电机结构图
该电机动子和定子轭部均由水平方向轧制的有取向硅钢制成,而齿部均由竖直方向轧制的有取向硅钢制成,图15为50CS350和35Q145两个牌号硅钢片的B-H曲线,由于有取向硅钢沿轧制方向和垂直轧制方向磁导率的不同,因此它们的B-H曲线有差异。
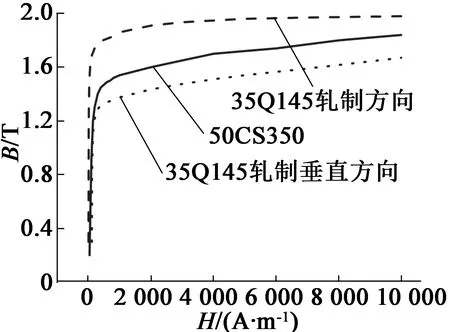
图15 两种硅钢材料的B-H曲线对比图
3.1 轧制角优化
考虑到LSRM部分磁力线不是沿水平或竖直方向,如图16所示。

图16 LSRM磁力线分布图
磁力线在定子、动子齿部中部沿竖直分布,但在齿部、轭部交界处磁力线有一定角度的弯曲,因此可以对有取向硅钢片轧制角度进行研究,如图17所示。

图17 轧制角示意图
图17中,θ1、θ4分别为动子、定子轭部硅钢片轧制方向同水平方向的夹角,θ2、θ3分别为动子、定子齿部硅钢片轧制方向同竖直方向的夹角,这些夹角的变化会对电机推力产生影响。
推力随动子、定子齿轧制角θ2、θ3的变化如图18所示。由图18可知,动子齿轧制角θ2在10°、定子齿轧制角θ3在0时平均推力达到最大,可见动、定子齿轧制角对推力的影响较大。
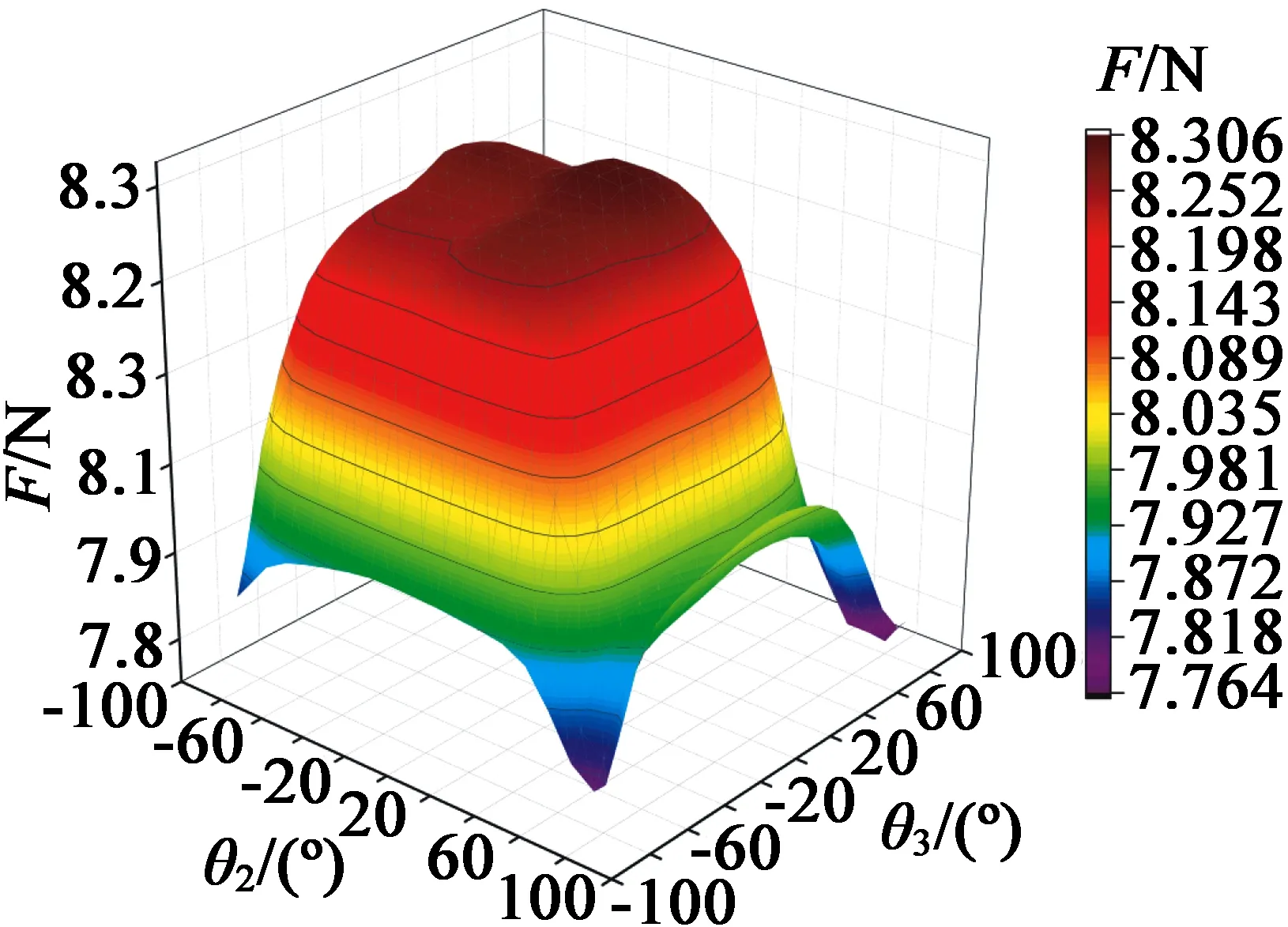
图18 平均推力随θ2、θ3的变化
平均推力随θ1、θ4的变化如图19所示。由图19可知,θ1、θ4的变化对平均推力影响很小,在轧制角为0时的平均推力依旧最大,因此动、定子轭的轧制角均选择0,可见电机动子、定子轭部硅钢片的轧制角度对推力影响较小,磁力线发生弯曲处主要集中在齿部上。
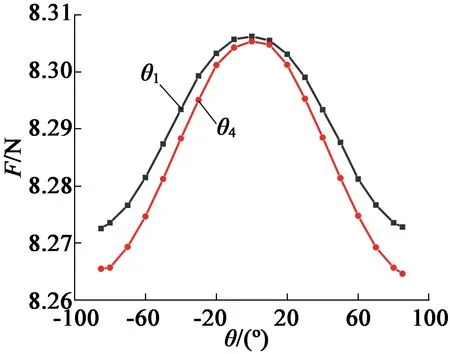
图19 平均推力随θ1、θ4的变化
3.2 优化前后对比
使用两种不同硅钢材料的推力对比如图20所示,平均推力由7.883 N增大到8.306 N,平均推力增长了5.37%。
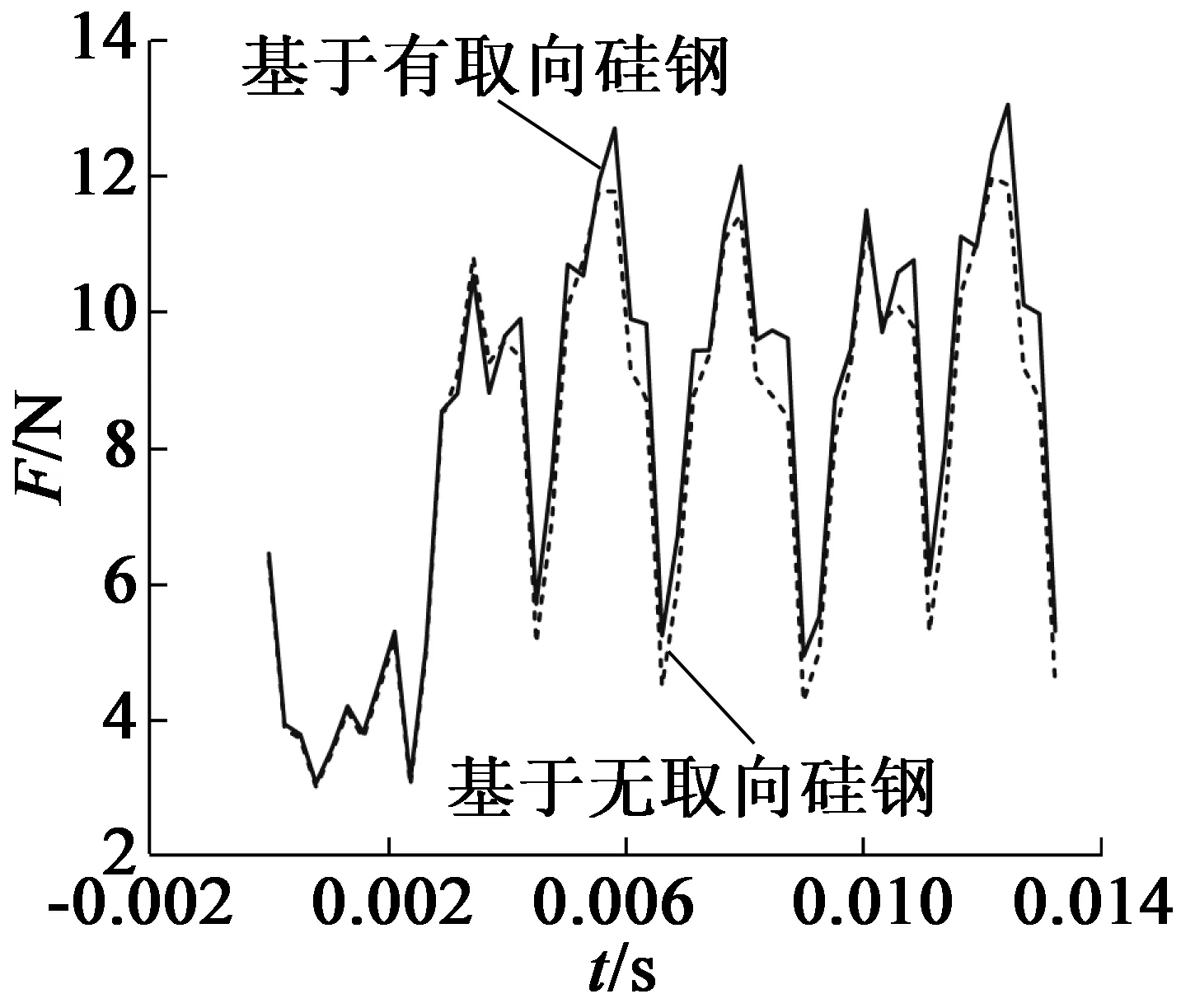
图20 使用两种不同硅钢的电机推力对比图
4 推力波动优化
由于LSRM在换相时具有较大的推力波动,该推力波动对于电机的平稳安全运行有较大影响,因此考虑对推力波动进行抑制。考虑对动子齿部进行优化,研究开切向槽对推力波动的影响,动子优化结构如图21所示,硅钢材料使用有取向硅钢35Q145作为研究对象,分别考虑槽的高度h1、深度d1、宽度h2对推力及推力波动的影响。

图21 动子开切向槽结构图
为了研究推力及推力波动的变化,特选择稳态推力作为研究对象,即动子在加速完成后的推力。
稳态推力随切向槽高度h1的变化如图22所示。可见,随着h1的增加,稳态平均推力近似线性增加,而稳态推力波动在h1为1.3 mm时处在一个拐点,此后h1增加对推力波动的增加逐渐放缓。

图22 h1变化对推力的影响
稳态推力随切向槽宽度h2的变化如图23所示。稳态平均推力和推力波动与h2呈反比关系,并在h2为1.7 mm后推力波动降低幅度增加,平均推力呈现先增后减的趋势,稳态平均推力总减小量为0.06 N,因此可取推力波动最小点,h2为2.5 mm。

图23 h2变化对推力的影响
稳态推力随切向槽深度d1的变化如图24所示。可见,d1的变化对推力和推力波动的影响较大,且为反比关系,当d1为2.5 mm时,稳态推力及推力波动均达到最小。
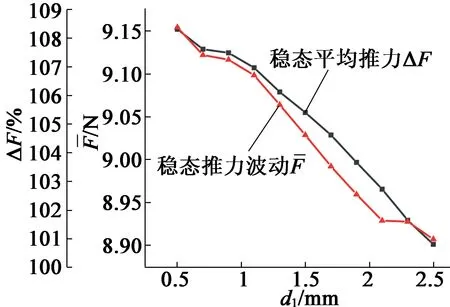
图24 d1变化对推力的影响
考虑到降低稳态推力波动的同时,尽量减少对稳态推力的影响,最终选择h1为0.9 mm,h2为2.5 mm,d1为1.5 mm,优化前后数据如表2所示。

表2 优化前后对比
优化后稳态推力相较于优化前降低了1.43%,但与此同时稳态推力波动降低了11.4%,可见动子齿部沿切向方向开槽具有较好的降低推力波动的效果,且对推力的影响也较小,有较强实用性。
5 结 语
本文设计了一种LSRM,首先推导了该电机的电磁方程,并从导通顺序、初始位置及电机结构三方面进行分析,对其进行了推力优化;然后提出将有取向硅钢应用于该电机的方案,确定了有取向硅钢的材料35Q145,研究了不同轧制角对推力的变化,推力有一定幅度的提升;最后提出动子齿部开切向槽减小推力波动的方法,仿真结果表明,此方法对推力波动的减小效果较好,对推力的影响也相对较小。

