开绕组无刷双馈发电机直接功率自抗扰控制策略
杨小亮,孙建新,王延峰,申永鹏,王明杰,王宇豪
(1.郑州轻工业大学 电气信息工程学院,郑州 450002;2.河南省信息化电器重点实验室,郑州 450002)
0 引 言
近年来,不可再生能源的过度开发利用,导致严重的生态环境问题,制约了社会的发展与进步,因此,可再生能源日益受到各国政府的重视和关注[1]。其中风能的利用技术相对成熟,而且设施日益完善,大量生产使其成本不断降低,并且风能具有清洁、无限循环利用的特点,被公认为最具商业开发前景的可再生能源之一[2]。作为近年发展起来的一种新型发电机,无刷双馈风力发电机具有变速恒频恒压发电、取消电刷滑环结构、功率因数可调等优点,是目前代替主流有刷双馈风力机的重要方向[3]。普通电机是将定子三相的一端或两端连接起来,将普通电机三相绕组的连接端解开,在绕组两端各引出三个接线端子,并在该绕组两端各接一个变流器,构成开放式绕组馈电的拓扑结构,绕组采用这种结构的电机被称为开绕组[4]电机。文献[5]首次对开绕组电机进行研究,实验研究发现,此电机通过各逆变器的相互协调,能有效提高开绕组电机转矩响应速度和频带范围[6]。后来国内外学者将直接转矩控制[7]和直接功率控制[8](以下简称DPC)等控制方法应用到开绕组无刷双馈发电机(以下简称OW-BDFG)中,不仅证明了控制策略的可行性和有效性,也为这种新型结构电机的应用和推广提供了有价值的理论参考依据和必要的技术支持。
韩京清教授提出的自抗扰控制技术[9-10](以下简称ADRC)广泛应用于无人机[11]、船舶[12]、电机控制[13]等多个领域。ADRC吸取了现代控制理论的成果,在PID技术的基础上,通过构造跟踪微分器、扩张状态观测器、非线性状态误差反馈控制率,加上若干个非线性函数和各个整定值的配合,组合出高品质的自抗扰控制器。
当前,大多数BDFG的控制研究还处于研究探索阶段,在双馈电机控制理论的基础上,将控制方法移入到无刷双馈电机中,并对其进行不断的完善是目前无刷双馈电机研究的重要途经。目前常见的控制方法有:(1)标量控制[14],通过PI调节器实现给定,该控制算法对硬件要求不高,实现简单,但动态性能指标较低;(2)矢量控制[15-16]利用解耦控制的思想,实现了对有功功率和无功功率的解耦控制,研究表明,矢量控制动态性能优良,调速范围宽,但该控制方法计算复杂且对参数的精度要求较高;(3)直接转矩控制[17-19]是通过测量三相定子电压和电流来计算磁链和转矩,并通过磁链和转矩的直接跟踪来实现对电机的控制,该控制性能优越,无需复杂的解耦思想,但低速时存在磁链和转矩脉动大等缺点。为进一步提高电机控制系统的有效性和鲁棒性,国内外专家学者提出了多种新型的控制策略,如间接转矩控制[20-21]、模糊自适应PID控制[22]、专家自适应PID控制[23-24]等,这些新型的控制策略不仅加快了系统响应,并且对电机动、静态性能有了进一步提升。
通过对开绕组发电机和自抗扰控制器的深入分析,本文研究了一种OW-BDFG的直接功率自抗扰控制策略,通过推导控制绕组侧电压与功率绕组侧有功功率和无功功率之间的关系方程,设计了自抗扰控制器,实现了对系统功率绕组侧的有功功率和无功功率的解耦控制。该控制策略不需要使用控制绕组侧电流回路,提高系统的反应速度,当被控对象参数发生变化时或有不确定扰动时具有较强的抗干扰性和鲁棒性,同时克服了传统DPC频率不固定、静差大等缺点。在MATLAB/Simulink平台上搭建OW-BDFG的直接功率自抗扰控制系统,通过仿真证明该状态方程的正确性以及控制方法的有效性和鲁棒性。
1 OW-BDFG模型和DPC模型
1.1 OW-BDFG变速恒频发电机理
OW-BDFG变速恒频风力发电系统结构组成如图1所示,主要包括风力机、增速齿轮箱、功率绕组和分开表示的控制绕组、控制绕组机侧双变流器(以下简称MSC)、网侧变流器(以下简称GSC)以及隔离变压器等。其中,功率绕组直接与工频电网相连,因控制绕组能量流动的双向性,故机侧和网侧均需采用双向可逆变流器,再经隔离变压器与电网相连。
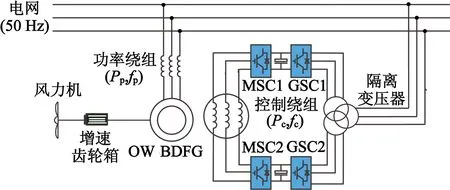
图1 OW-BDFG的变速恒频风力发电系统
如图1所示,BDFG稳态运行时,电机的转速与绕组频率,绕组极对数pp,pc的关系:
(1)
式中:nr为发电机转速;下标p,c为功率绕组和控制绕组;pp,pc为电机的极对数;fp,fc为电机的绕组频率。
当电机运行时,转速大于同步速时,发电机为超同步运行状态,fc取负值,表示控制绕组电流相序与电机转向相反;反之,当电机转速小于同步速时,发电机为亚同步运行状态,fc取正值,控制绕组电流相序与电机转向相同。极对数不会变化,当转速发生变化时,若想保证功率绕组频率不变,由式(1)可知,只需调节控制绕组频率即可。
1.2 OW-BDFG数学模型
在本文中,OW-BDFG采用两相d,q坐标系数学模型[25],电压方程:
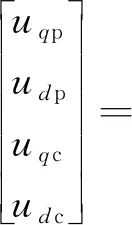
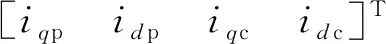
(2)
磁链方程:
(3)
由式(2),式(3)可得:
(4)
式中:u,i为电压和电流;ψ为磁链;R为电阻;Lp,Lc,Lm为功率绕组自感、控制绕组自感以及功率绕组与控制绕组间的互感;ω和ωr-ω分别为功率绕组和控制绕组任意速旋转参考坐标系的角速度;下标d,q为分别表示d,q坐标系下d轴和q轴分量;p=d/dt为微分算子。
根据瞬时功率理论[26-27]可知,OW-BDFG功率绕组输出的瞬时有功功率P和无功功率Q表达式分别如下:
(5)
1.3 DPC模型
由于OW-BDFG的功率绕组直接与电网相连,可以近似认为功率绕组的电压幅值、频率均为定值,所以一般选择电压定向或磁场定向方式[28]。本文采用功率绕组定子磁链定向,将同步旋转d,q坐标系的d轴定向在定子磁链Ψp方向上,此时,d,q轴上的磁链分量分别为:|Ψdp|=|Ψp|,|Ψqp|=0。功率绕组频率为工频,功率绕组电阻忽略不计,感应电动势e近似等于定子电压,根据发电机惯例,感应电动势e滞后于磁链Ψp90°,所以e位于q轴负方向,则有|uqp|=|up|,|udp|=0。
|Ψdp|=|Ψp|,|Ψqp|=0,结合式(3)可知:
(6)
则由式(6)得:
(7)
将式(7)代入ψqc=Lciqc-Lmiqp中,整理得:
(8)
又由式(6)得:
(9)
将式(9)代入式ψdc=Lcidc+Lmidp中,整理得:
(10)
将式(8)、式(10)分别代入式(7)、式(9)中,整理得:
(11)
将|uqp|=|up|,|udp|=0,代入式(5),并整理得:
(12)
式中:up是定子电压矢量的幅值,为常数。
将式(11)代入式(12)中,得有功功率P和无功功率Q分别如下:
对时间t进行微分,则有功功率P和无功功率Q的导数表达式:
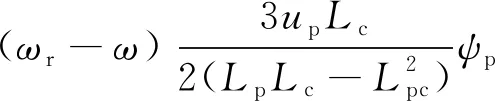
(14)
(15)
通过研究控制绕组侧电压与功率绕组侧有功功率和无功功率间的关系,建立了基于d,q坐标系的DPC状态方程。在此基础上,设计自抗扰控制器,以此验证上述状态方程的正确性和该新型控制策略的有效性。
2 BDFG直接功率ADRC系统
2.1 二阶自抗扰控制器的结构及各部分功能
典型的自抗扰控制器由非线性跟踪—微分器(以下简称TD)、扩张状态观测器(以下简称ESO)和非线性状态误差反馈控制率(以下简称NLSEF)组成[29],如图2所示。
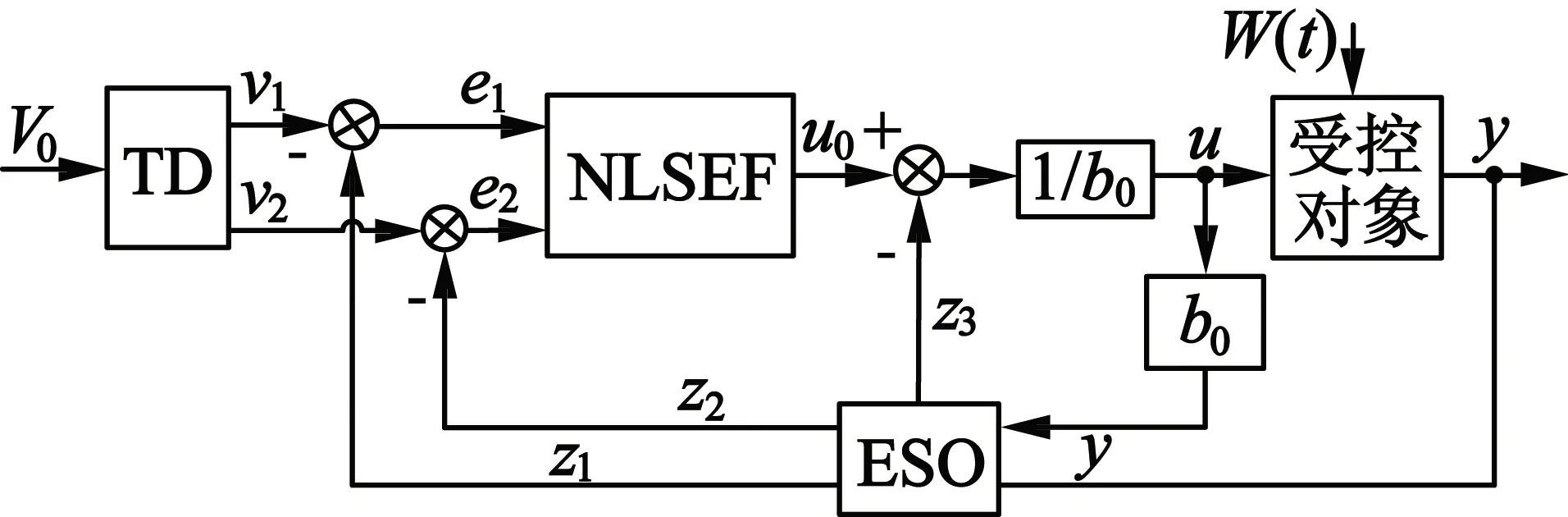
图2 二阶自抗扰控制器结构图
TD用来获得合理的微分信号并安排过渡过程,以此实现快速无超调跟踪,可在一定程度上解决超调和快速性之间的矛盾。
ESO用来对系统未知模型部分和不确定外扰的总和控制量进行实时估计,根据被控对象的输出和输入来估计被控对象的状态量z1,z2和总扰动量z3。
NLSEF利用TD和ESO的输出之间的差值来生成对象所需的控制量,并对扰动量进行补偿,以此构成最终的控制作用。
2.2 二阶自抗扰控制器设计
采用二阶TD算法,构造最速离散跟踪微分器:
(16)
其中函数fhan(x1,x2,r,h0)算法:
(17)
式中:h为积分步长,积分步长的缩小对抑制噪声放大起重要作用,但计算次数增多;h0为滤波因子,扩大滤波因子可增强滤波效果,同时也降低了跟踪速度;r为速度因子,速度因子越大跟踪速度越快,但相应的滤波效果会变差;sign函数为符号函数。
在此设置参数h与h0为0.01,根据系统对响应所需要的调节时间,调节速度因子r,直到达到本文满意的曲线;参数h和r需相互配合才达到快速跟踪的效果。
ESO是自抗扰的核心部分,建立非线性扩张状态观测器:
(18)
式中:幂次函数fal(·)为表达式如下,
(19)
式中:δ>0;z1,z2和z3为状态量x1,x2和x3的跟踪值;β1,β2,β3,b,a1,a2,d,α,δ为参数。
取a1=0.5,a2=0.25,调节参数的过程中,从β1开始,依次调节β2与β3,注意β3不能因为过大而引起超调,与此同时β3与b0之间相互配合,这两个参数对系统的扰动补偿起重要作用。
通过TD和ESO的输出误差得到控制量u0,NLSEF:
(20)
式中:c,r,b0和h1为参数。
fhan的算法同上,其中h1与h的取值一样,c决定了NLSEF响应速度的快慢,参数r也参与了调节系统响应的过程,参数b的取值一般与b0相等。
3 基于自抗扰控制器的BDFG的DPC系统
针对OW-BDFG模型的复杂性和强耦合性等问题,本文建立了控制绕组侧电压与功率绕组侧有功功率和无功功率间的关系,通过自抗扰技术来实现对OW-BDFG有功和无功功率的解耦控制。
有功功率P的动态过程由式(14)表示,无功功率Q的动态过程由式(15)表示。利用MATLAB/Simulink仿真软件搭建ADRC系统,合理选取ESO参数,通过适当的补偿来抵消功率绕组和控制绕组之间的交叉耦合,将式(14)和式(15)中的非线性项与耦合项看作系统的内部扰动,根据ADRC原理和图2,结合OW-BDFG内部电压与功率间的关系,建立了基于ADRC的BDFG的DPC仿真模型,如图3所示。
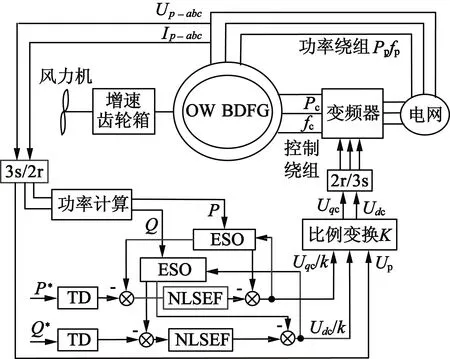
图3 OW-BDFG直接功率自抗扰控制系统框图

OW-BDFG与ADRC系统的相关参数如表1、表2和表3所示。
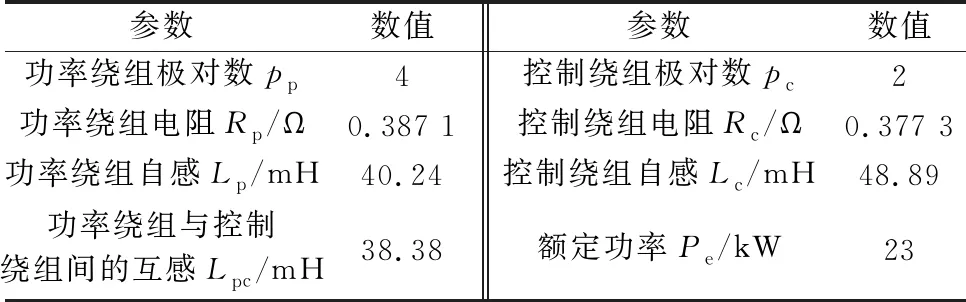
表1 OW-BDFG相关参数
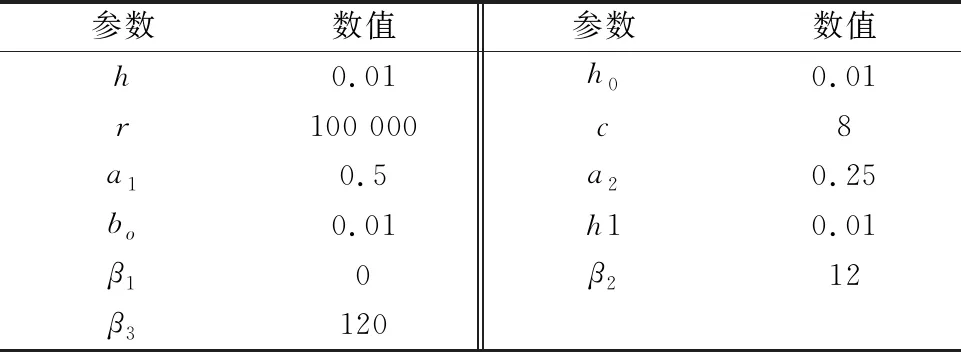
表2 有功功率ADRC相关参数
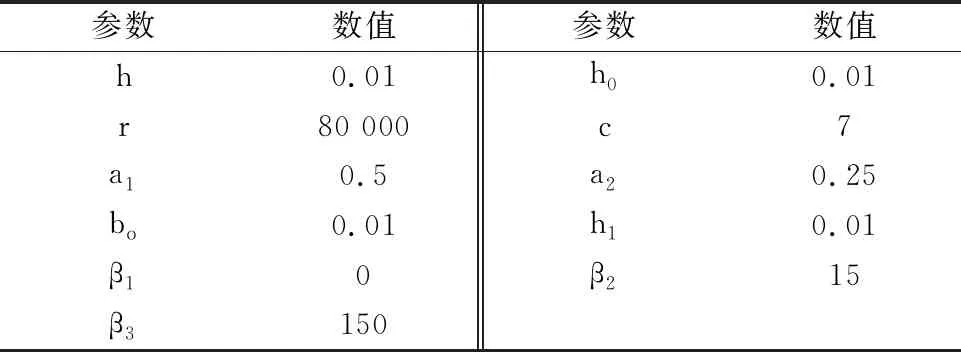
表3 无功功率ADRC参数
4 仿真结果分析
利用MATLAB仿真软件搭建BDFG直接功率ADRC系统,给定转速、有功功率、无功功率参数,在相同条件下与传统滑模控制进行仿真对比,并进行功率绕组电流的谐波分析,以此来说明BDFG直接功率ADRC策略中所推导功率模型的正确性及稳态条件下系统的控制性能;在稳定状态下,外部转速发生变化,通过对系统有功和无功功率跟踪波形的分析,得到系统的动态性能和抗外部干扰的能力;当电机参数发生变化时,有功和无功功率在经过短暂的波动后能够较快地跟踪设定的参考值,说明了控制系统抗内部参数扰动的能力。
4.1 转速恒定时的特性
首先,设定转速为400 r/min,有功功率给定值为5 000 W,无功功率给定值为-5 000 W,在相同条件下分别进行BDFG直接功率ADRC与普通滑模控制[30]仿真,结果如图4和图5所示,仿真波形包括有功功率、无功功率和功率绕组三相电流,以及控制绕组三相电流。

(a) 有功功率
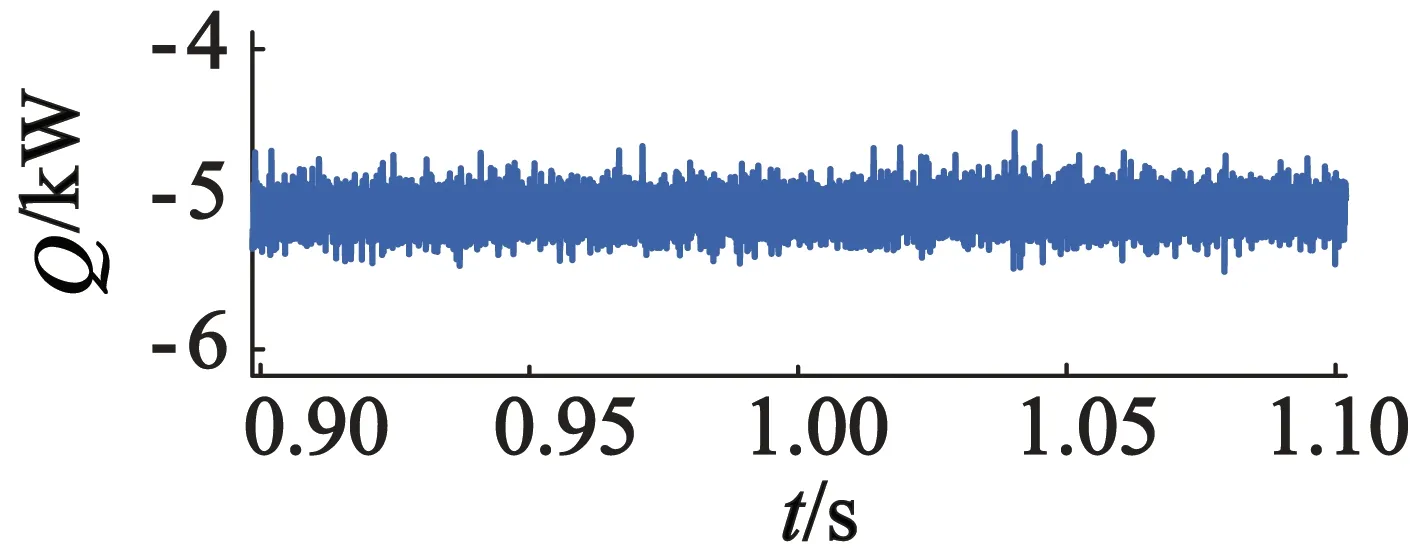
(b) 无功功率
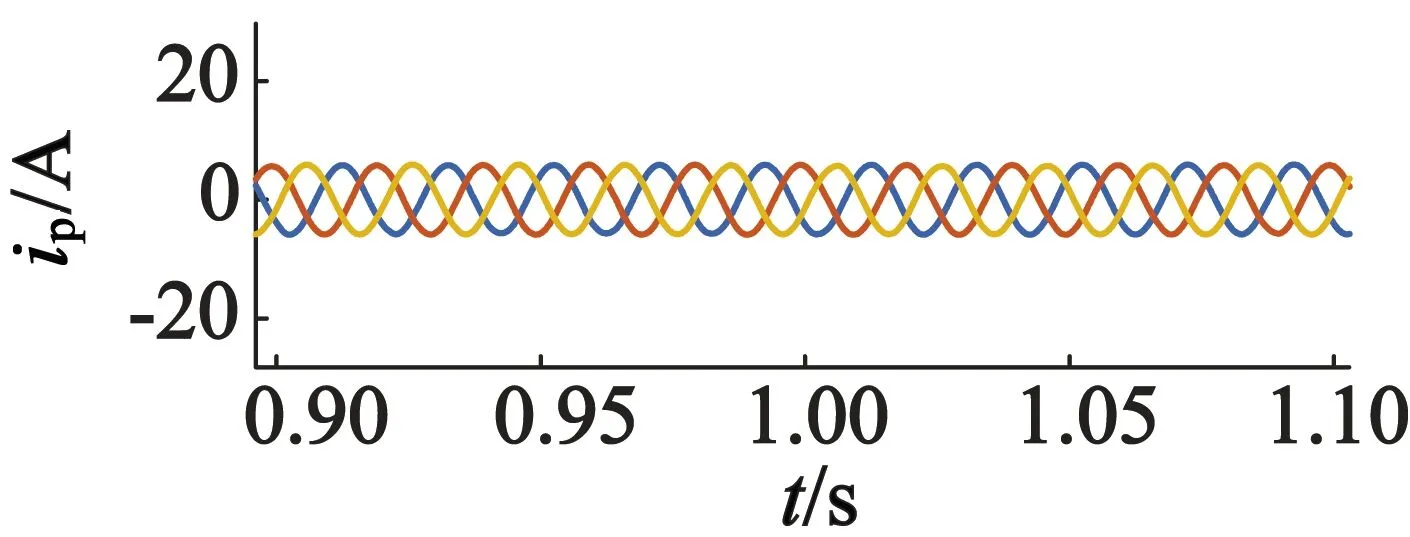
(c) 功率绕组电流
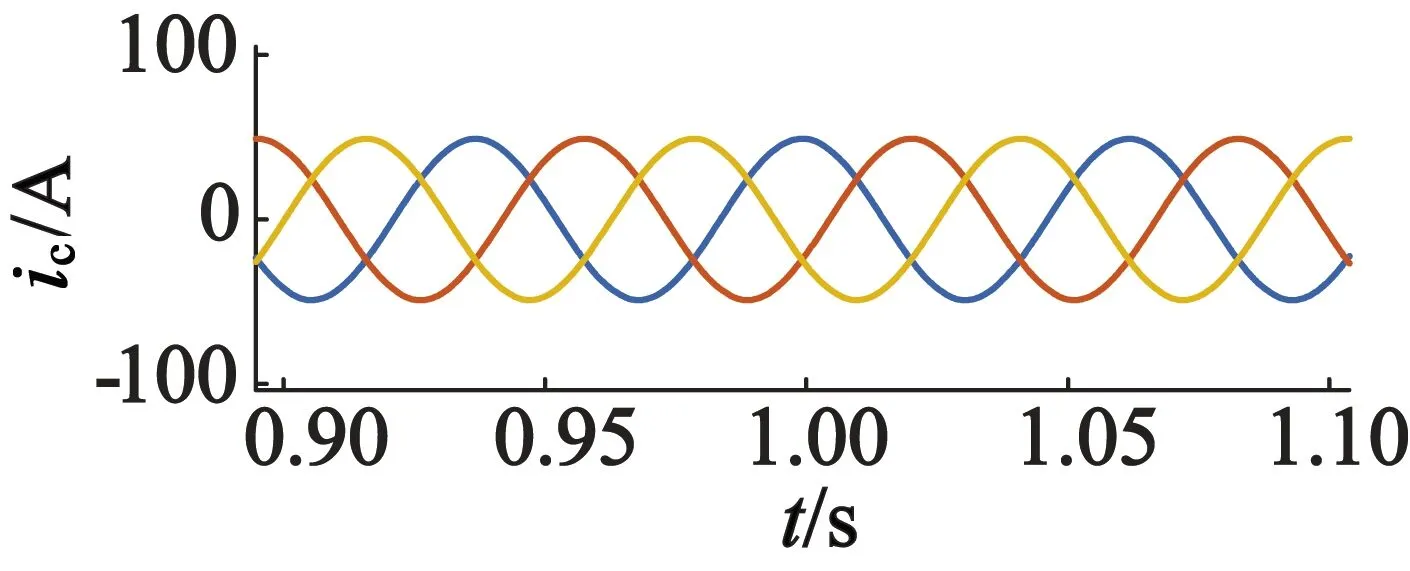
(d) 控制绕组电流
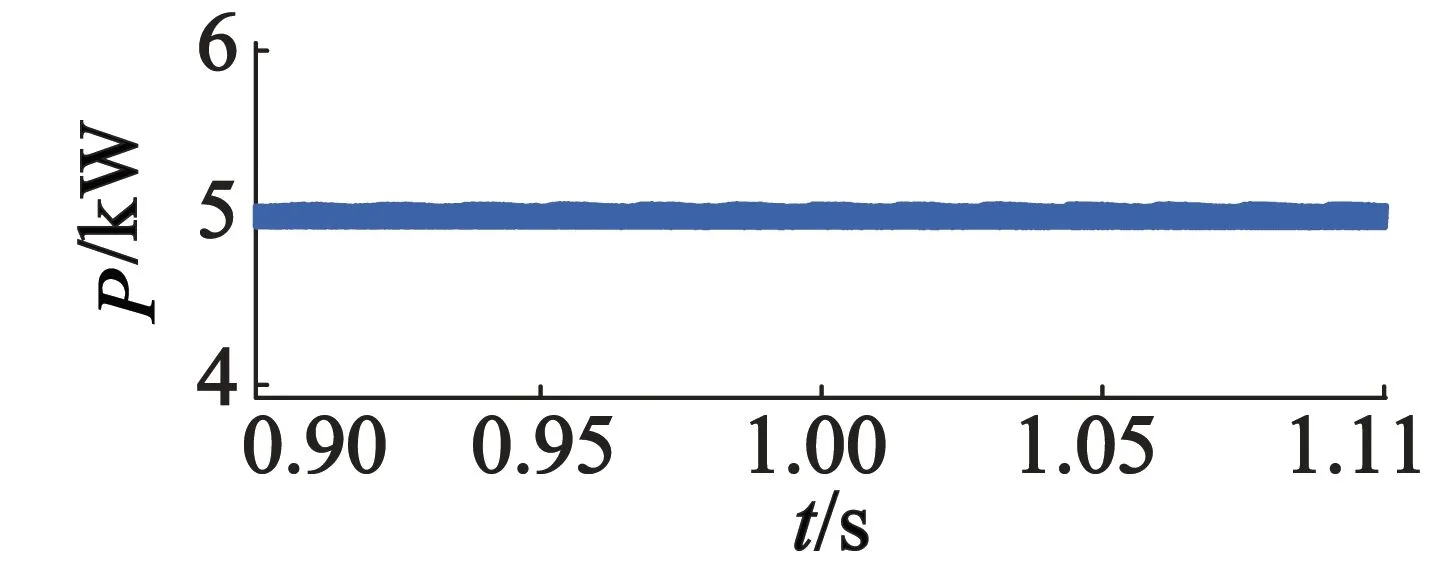
(a) 有功功率
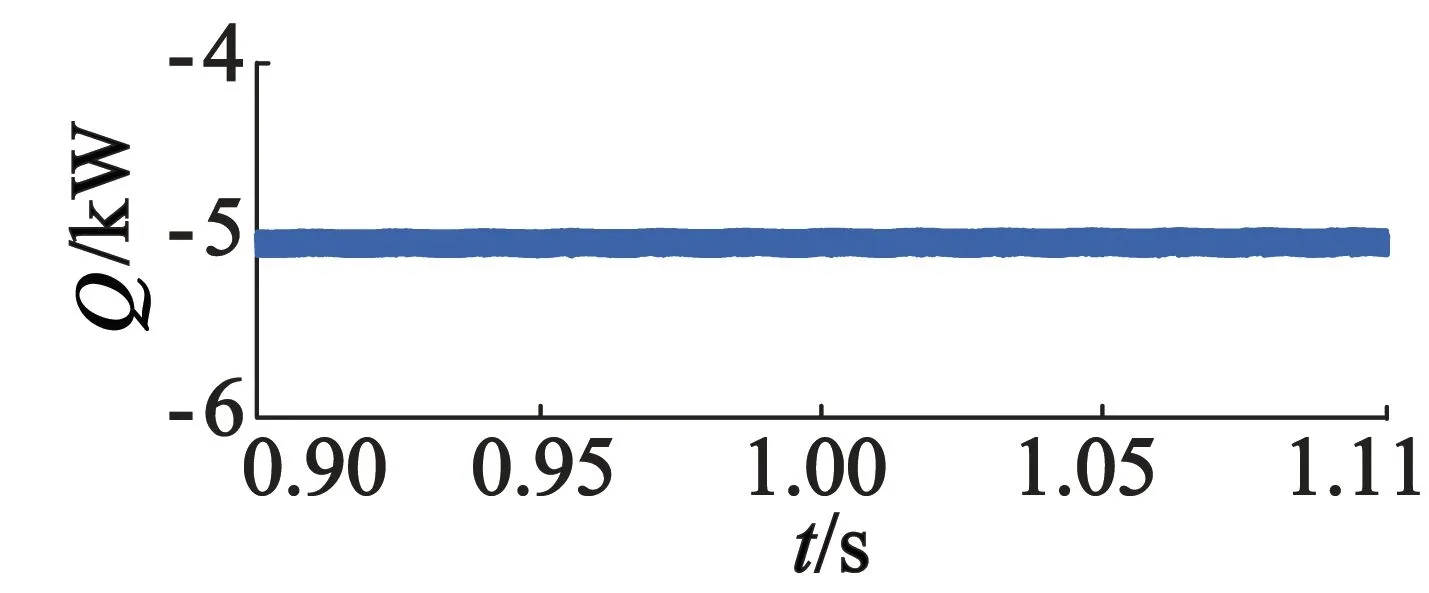
(b) 无功功率
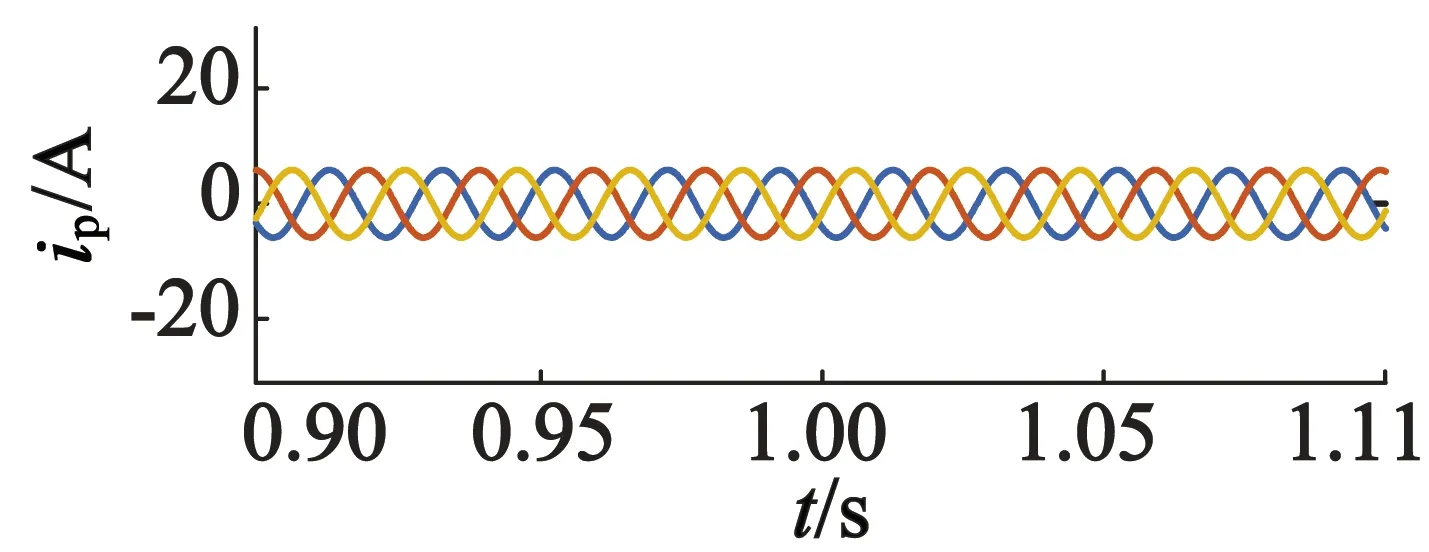
(c) 功率绕组电流

(d) 控制绕组电流
图4和图5仿真结果显示两种控制策略均能够实现对定子功率绕组有功功率和无功功率的独立控制,验证了所推导的BDFG直接功率状态方程的正确性及ADRC策略的可行性。对比图4和图5可以看出,两种方法都能够使有功功率和无功功率较好地跟踪设定的参考值,但BDFG直接功率ADRC系统输出的有功和无功功率纹波远小于普通滑模控制系统纹波,显示出良好的稳态性能。
滑模控制参数k1~k4如表4所示[30]。

表4 滑模控制参数
4.2 功率绕组电流谐波分析
图6和图7给出了普通滑模控制与ADRC相比较的功率绕组电流谐波图。在基频为50 Hz的条件下,从1 s开始,取功率绕组电流10个周期,进行电流总谐波畸变(以下简称THD)分析,从分析的结果可以看出,采用ADRC算法能够实现开关频率恒定,其电流谐波畸变仅为2.03%,满足并网电能质量的标准。
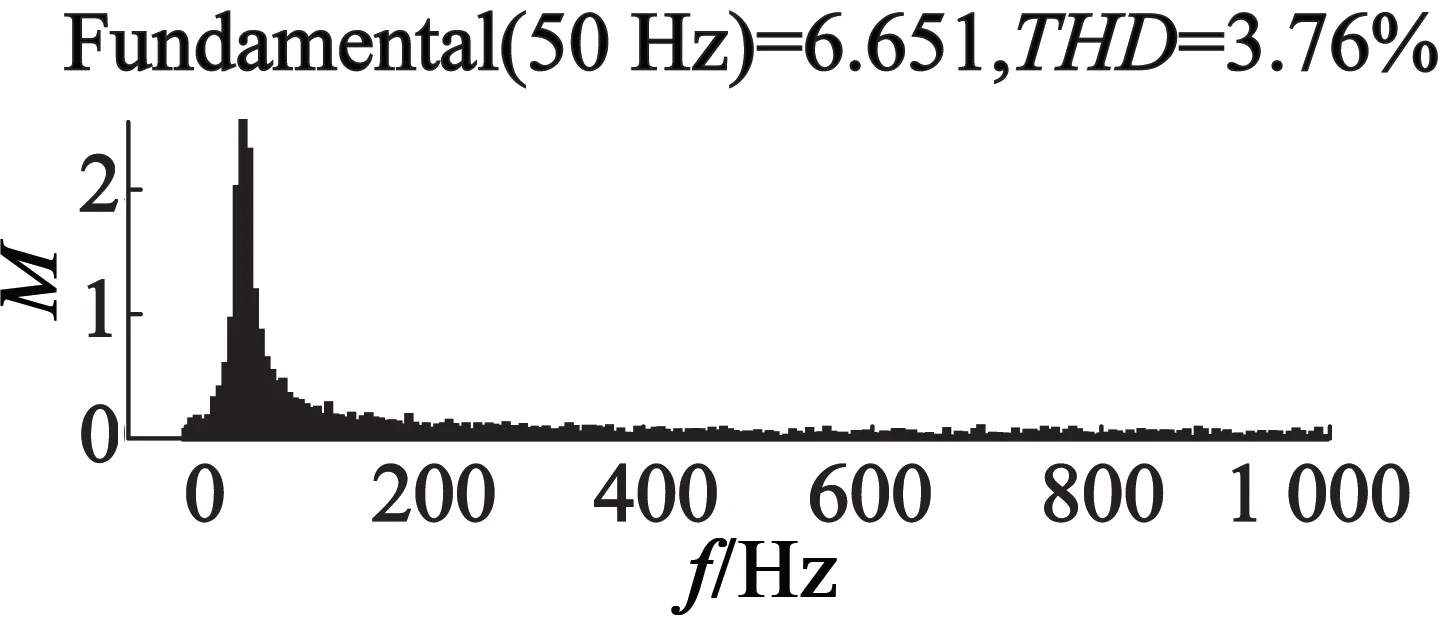
图6 滑模控制中的电流谐波分析

图7 ADRC中的电流谐波分析
4.3 转速变化时的特性
在1 s后,有功和无功功率给定值不变,在相同条件下,电机转速由400 r/min变化到480 r/min,电机动态波形如图8所示。由于自抗扰中ESO的补偿作用,电机转速上升变化的同时,有功和无功功率在经过短暂的振荡后,依然能够较快地跟踪设定的参考值;同时功率绕组电流的频率没有受到转速变化的影响,仍然稳定在50 Hz,控制绕组的频率能够根据转速的变化而变化,从而实现风力发电系统的变速恒频控制,显示出良好的抗扰动能力,也进一步验证了本文控制策略的正确性和有效性。
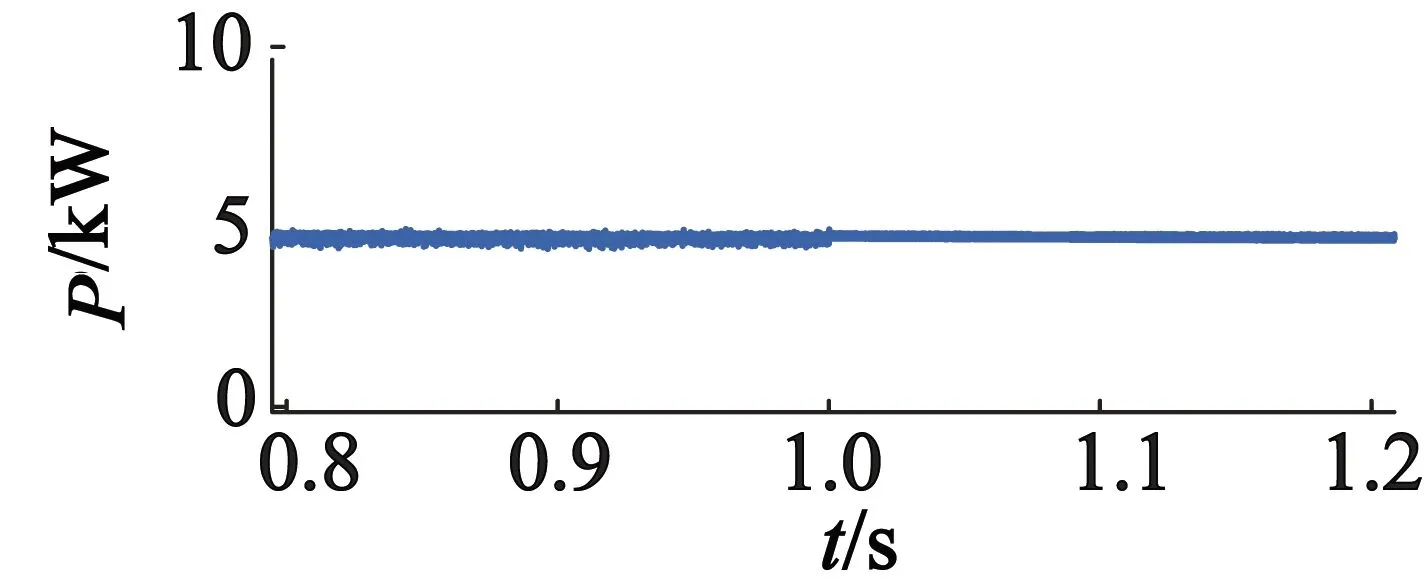
(a) 有功功率
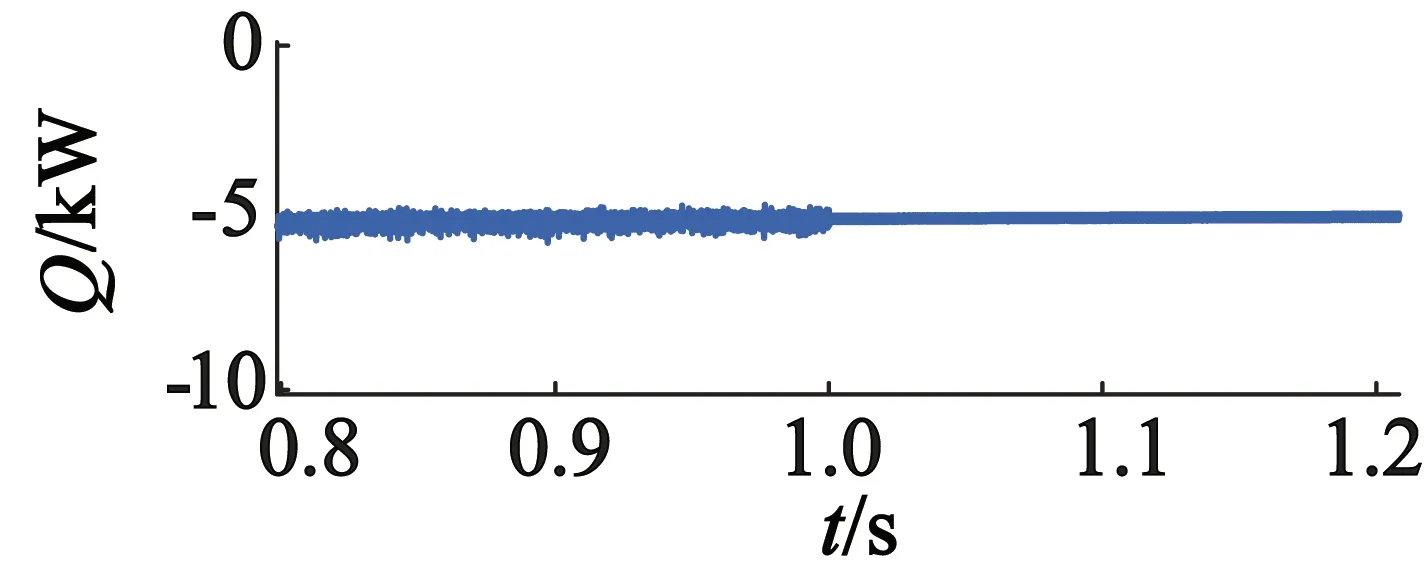
(b) 无功功率
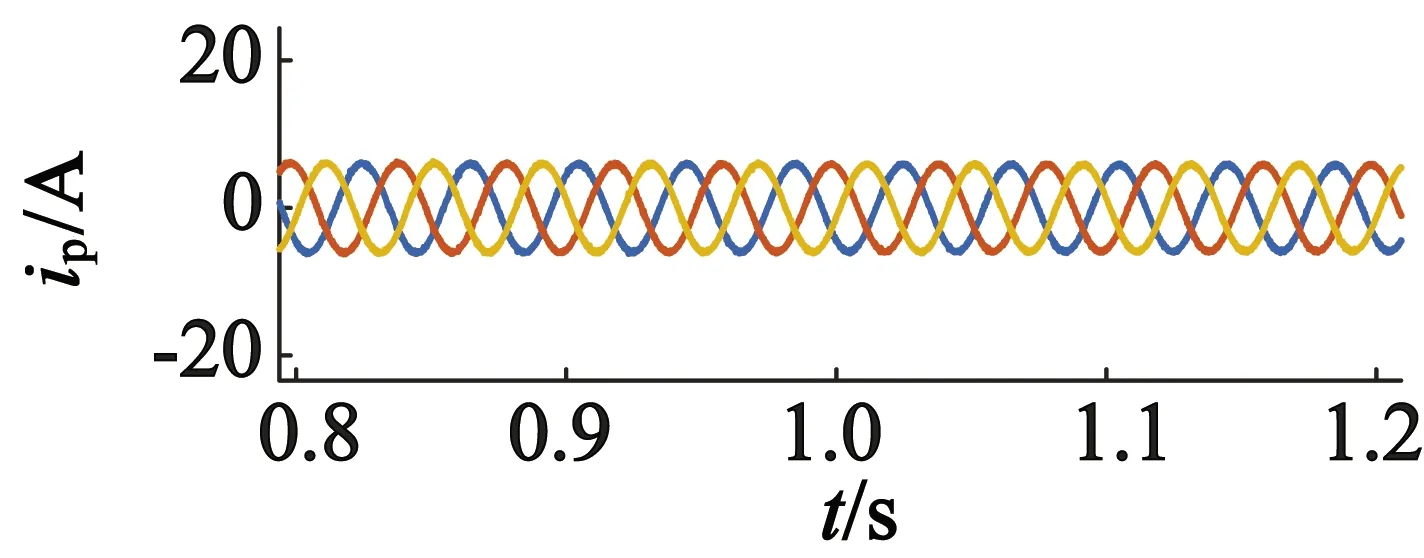
(c) 功率绕组电流
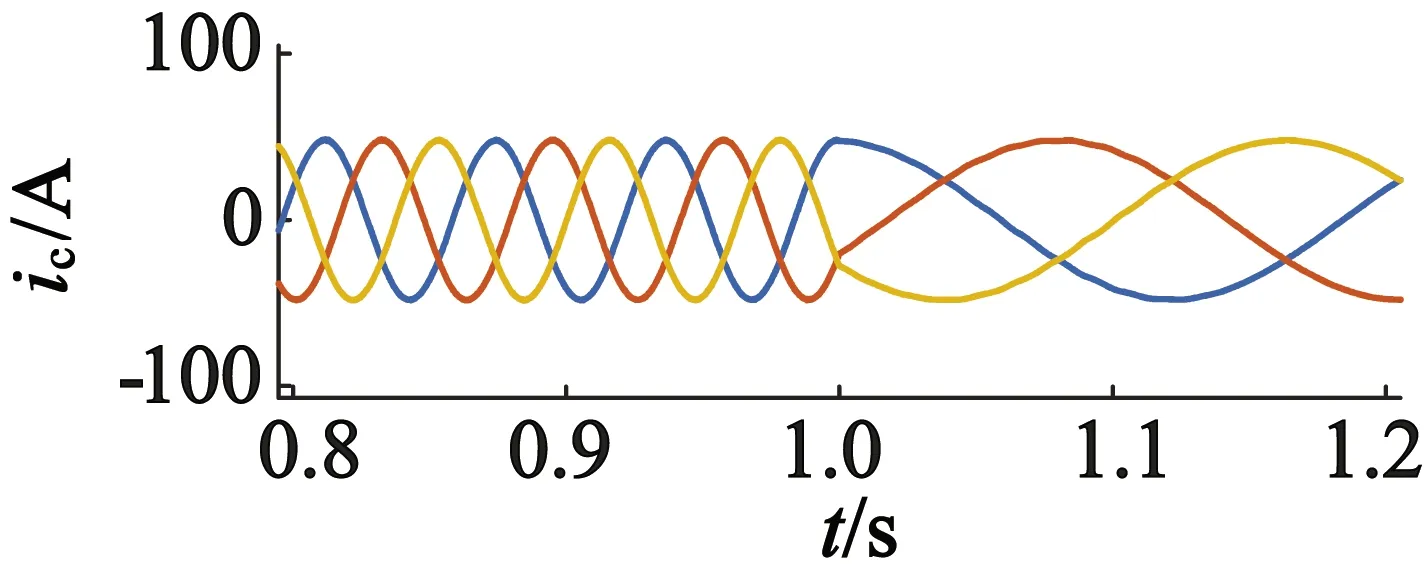
(d) 控制绕组电流
4.4 参数变化时的特性
系统在实际运行过程中,忽略定转子漏感,电机参数可能会因外界温度、集肤效应等发生变化[31-32]。为了验证仿真系统对参数变化的抗干扰性,在稳态运行的情况下,转速设定为400 r/min,有功和无功功率给定值依然不变,在1 s时将电机功率绕组和控制绕组的电阻与电感以及互感值增大10%,在相同条件下进行参数变化的仿真,仿真结果如图9所示。通过仿真结果可以发现,电机参数变化对系统的控制性能影响很小,有功和无功功率在经过短暂波动后继续稳定在设定参考值,功率绕组和控制绕组电流在经过短暂振荡后也能够较快地稳定在正常值,这样进一步证明了本文控制系统对内部参数扰动具有较强的抗干扰性能。
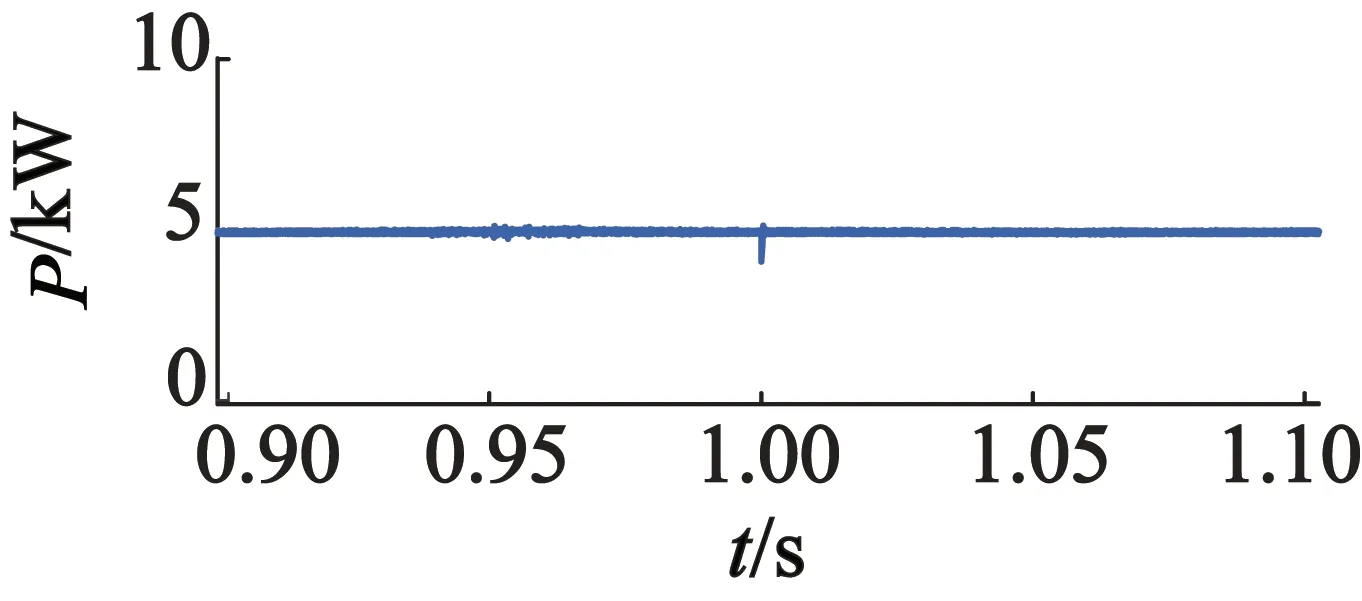
(a) 有功功率

(b) 无功功率
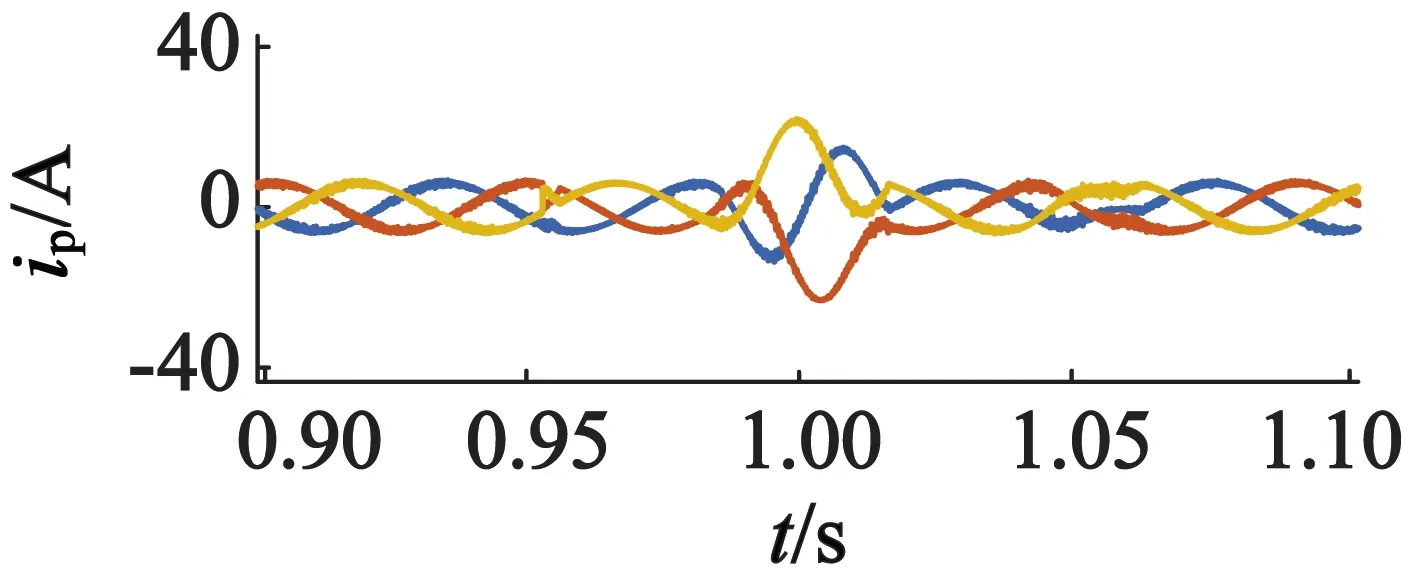
(c) 功率绕组电流
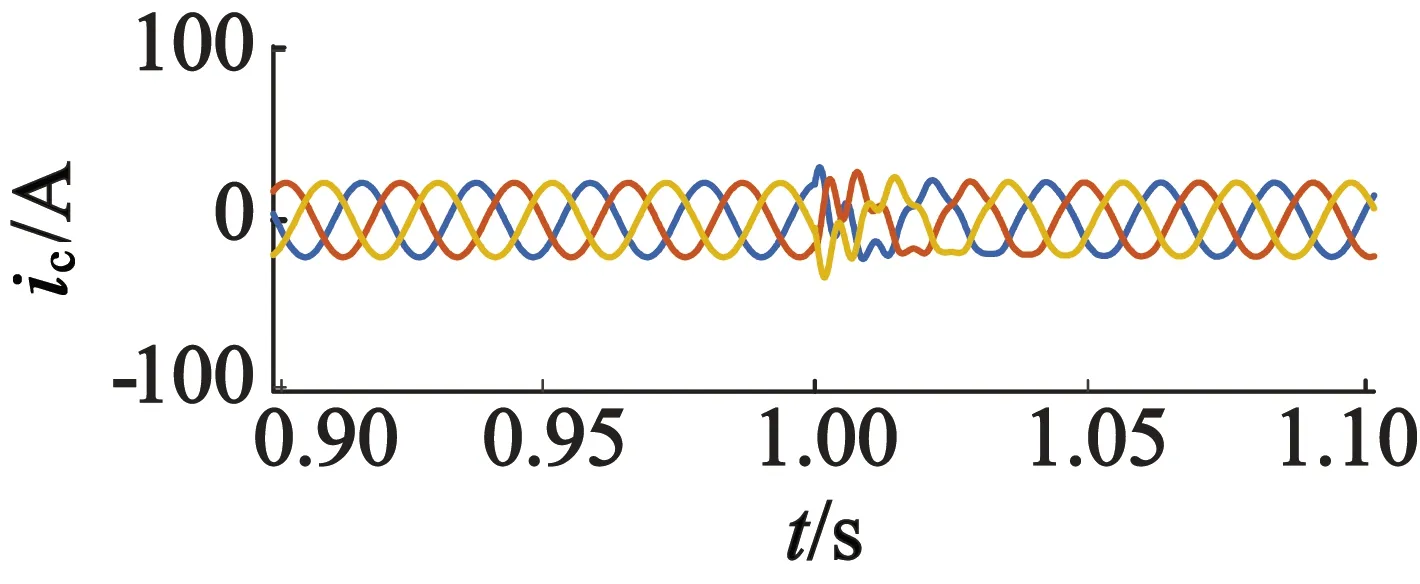
(d) 控制绕组电流
5 结 语
本文首先通过研究OW-BDFG控制绕组侧电压与功率绕组侧有功功率和无功功率间的关系,建立了基于d,q坐标系的DPC状态方程;在此基础上,设计自抗扰控制器,实现了对系统功率绕组侧有功和无功功率的解耦控制。通过仿真和对比研究,进一步验证了所推导直接功率状态方程的正确性及所设计的ADRC DPC策略的有效性,提高了控制系统的反应速度和系统抗外部及内部扰动的能力,且具有良好的动、静态性能和较强的鲁棒性。

