永磁同步直线电机的电磁设计与分析

史石磊，康尔良

(1.哈尔滨理工大学 电气与电子工程学院，哈尔滨 150080；2.黑龙江省高校直驱传动系统工程技术创新中心，哈尔滨 150080)

0 引 言

伴随着制造业的转型升级，数控机床向着高精度、高速度和高稳定性的方向发展。相比于传动旋转电机的传动机构，永磁同步直线电机传动机构具有功率密度大、响应速度快等特点，这使其在高精度机床进给系统中得到了广泛的应用，从而推动了永磁同步直线电机相关研究的发展[1-2]。

文献[3]针对有铁心永磁同步直线电机(以下简称PMSLM)的推力波动问题，提出了一种V型端部结构来消除永磁同步直线电机的端部磁阻力。文献[4]通过磁场解析并采用许可变换，计算出了圆筒型永磁同步电机的气隙磁密。文献[5]以Halbach阵列永磁同步电机为模型，通过解析法推导了初级长度与边端力最小的关系式，并以此来削弱初级的端部力。文献[6]以永磁同步直线电机为模型，分析了磁路饱和对电感的影响，得到了饱和效应引起的电感随着位置变化的规律，并用有限元法进行了验证。文献[7]利用二维有限元对Halbach圆筒型永磁直线电动机的磁场强度、感应电动势等参数进行了分析。上述文献中的研究都是基于既定的PMSLM模型上进行性能分析及优化，没有给出PMSLM的具体电磁设计方案及流程。

本文以一台额定推力610 N、额定速度3.2 m/s的PMSLM为对象进行电磁设计，初级采用有铁心的水冷结构，次级采用表贴式、斜极的永磁体结构。根据经典的旋转永磁电机的计算公式，推导出适合PMSLM的电磁计算公式，确定电机的主要结构尺寸。在此基础上，建立电机的二维有限元模型，对气隙磁密、反电动势波形和推力波动等性能进行分析和结构优化，得到最终的设计方案。

1 PMSLM结构

本文设计的PMSLM三维结构示意图如图1所示。绕组采用分数槽集中绕组，三相绕组嵌入在初级铁心的开口矩形槽中，初级铁心背面嵌入冷却管来提高电机散热能力。N，S两种充磁方向的永磁体依次粘贴在永磁体轭板表面。相对于旋转电机，直线电机很难实现铁心斜齿的结构，只能采用永磁体斜极结构来削弱PMSLM的定位力。

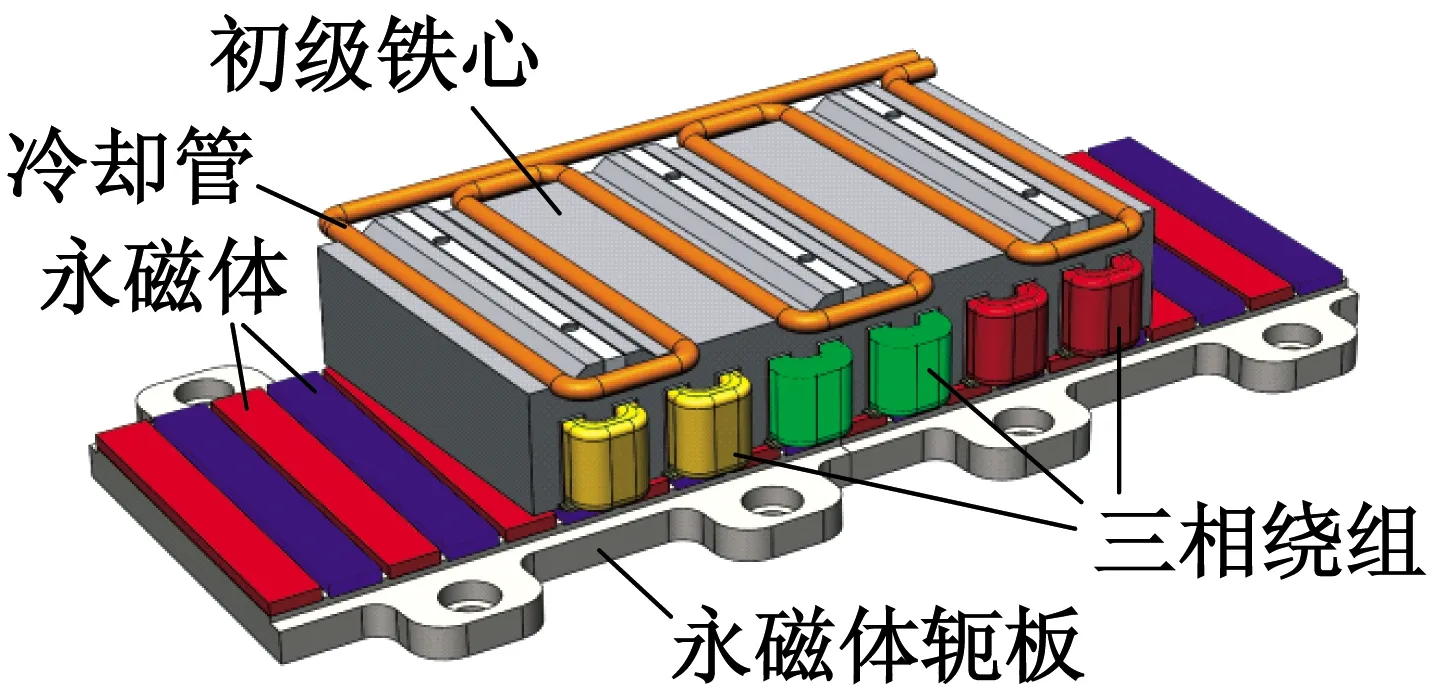
图1 PMSLM三维结构示意图

2 PMSLM电磁设计

2.1 主要尺寸计算

电机电磁设计的过程按照电磁设计程序确定一个合理的电磁方案，该方案需满足用户的技术性能指标的。电磁设计的首要任务就是确定设计目标，本文涉及PMSLM的设计目标如表1所示。

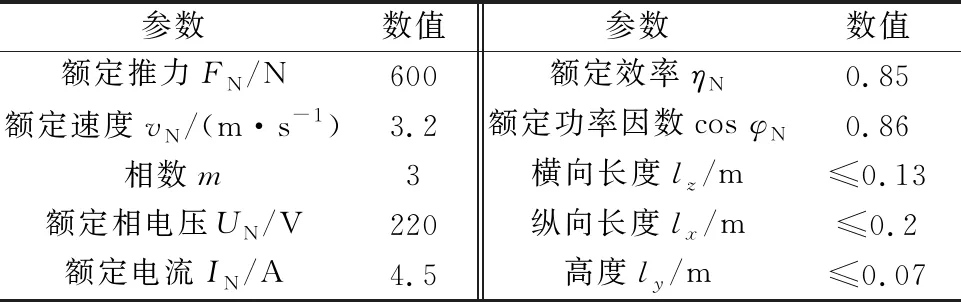
表1 PMSLM设计目标

PMSLM是通过电磁耦合进行机电能量的转换，即初级载流导体产生的交变磁场与次级永磁体产生的恒定磁场相互作用，将电能转换为机械能。根据机电装换能量原理，可得PMSLM输入功率P1、输出功率PN和电磁功率Pm关系：

PN=FNvN=mUNINcosφNηN=P1ηN

(1)

(2)

式中：1-εL为满载相电动势与相电压比值；E1为额定相电动势。额定相电动势E1的计算公式：

E1=4KmfNNKsKwΦ

(3)

式中：Km为气隙磁场波形系数；fN为相电势频率；N为绕组每相串联匝数；Ks为斜极系数；Kw为绕组系数；Φ为每极磁通。

PMSLM的速度与相电动势的频率关系：

vN=2τfN

(4)

式中：τ为极距。

每极磁通Φ：

Φ=Bδαiτlef

(5)

式中：Bδ为气隙磁密；αi计算极弧系数；lef为铁心计算叠厚。

电负荷A的计算公式：

(6)

整理式(1)～式(6)可得：

(7)

式中：2τp为纵向有效长度。取气隙磁场波形系数Km=1.25，斜极系数Ks=0.9，绕组系数Kw=0.93，气隙磁密Bδ=0.78 T，计算极弧系数αi=0.875，电负荷A=57 000 A/m，1-εL=0.91，计算可得：

(8)

S=0.018 m2,考虑横向长度不大于0.13 m，并需要预留两侧端部绕组所需尺寸，取lef=0.1 m,则有效长度2pτ计算公式：

(9)

2.2 初级绕组设计

为了尽可能使铁心齿槽及绕组的制造工艺简单，本文采用单层、星形分数槽集中绕组，并取槽数Q=12。槽数为12的常用极槽配合有8/12，9/12，10/12，11/12。如表2所示，给出了4种不同极槽配合下的绕组因数。为了使反电动势波形正弦性较好，选取基波绕组因数较大，且谐波绕组因数较小的极槽比。本文最终选取11极12槽的极槽配合，节距y=1，q=4/11，并联支路数a=1，并绕根数Nt=1，每相串联匝数372，每槽导体数Ns为186，接线图如图2所示。

表2 不同极槽比下的绕组因数

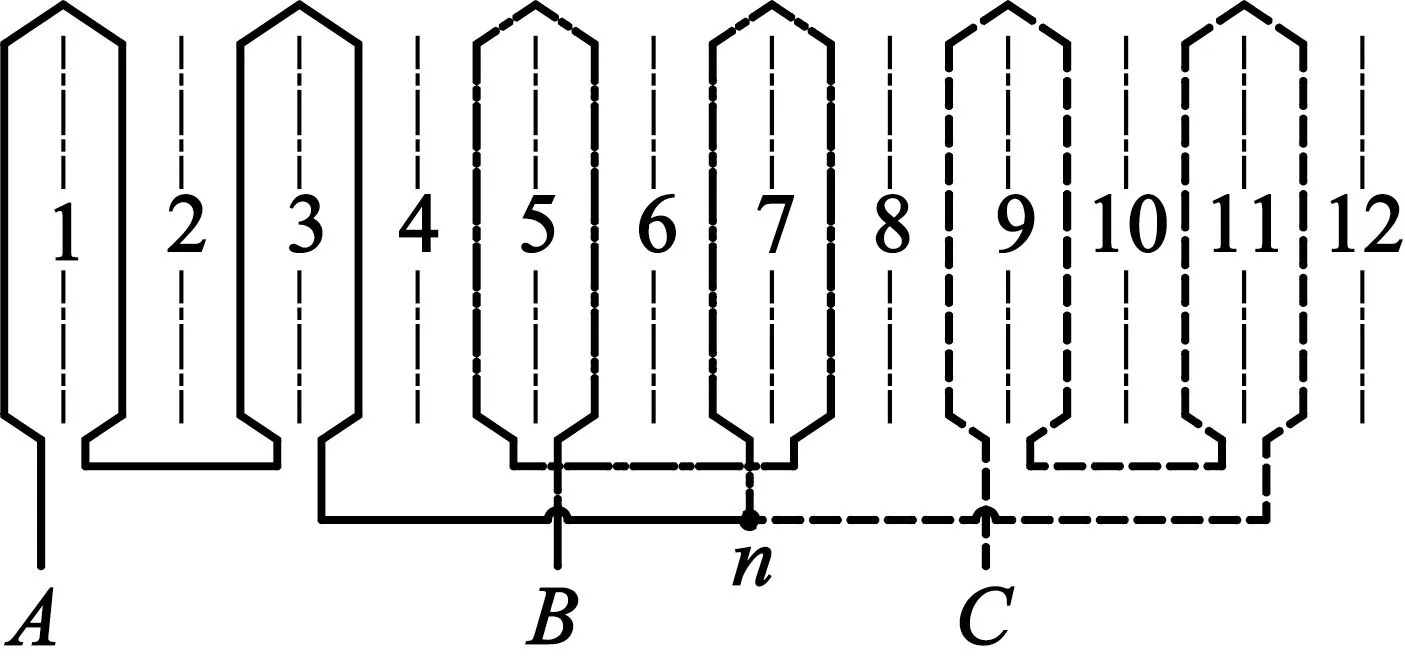
图2 11极12槽单层绕组星形接线图

取电密J=10 A/mm2，由于电密值较高会导致电机发热严重，所以采用水冷方式进行散热。由电密值和电流可计算出导线的裸线线径dCu=0.76 mm，根据漆包线绝缘厚度一般为0.06～0.09 mm，取带绝缘线径d=0.85 mm。

2.3 槽形设计

考虑下线工艺简单，本文采用开口矩形槽，槽形结构如图3所示。参考文献[8]中齿槽计算公式，计算出的具体尺寸参数如表3所示。

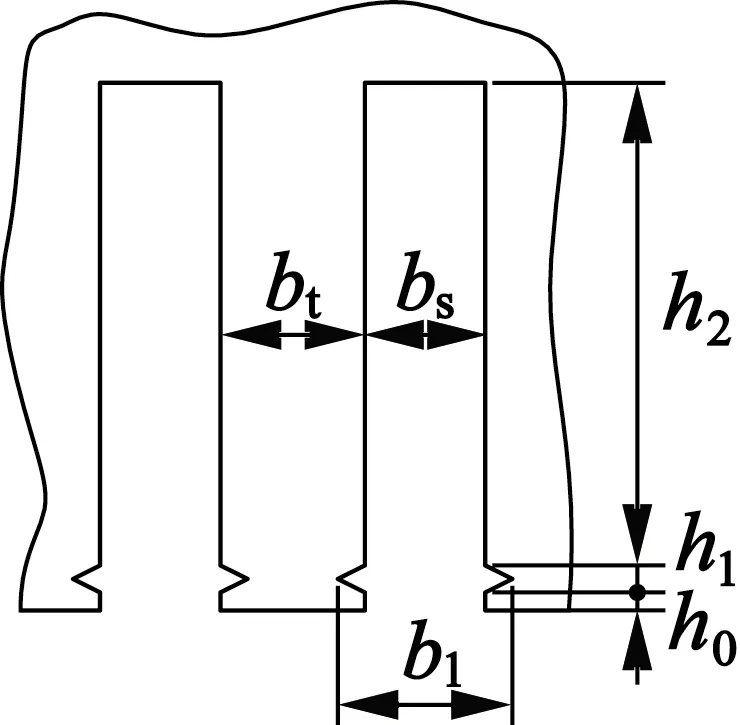
图3 PMSLM槽型

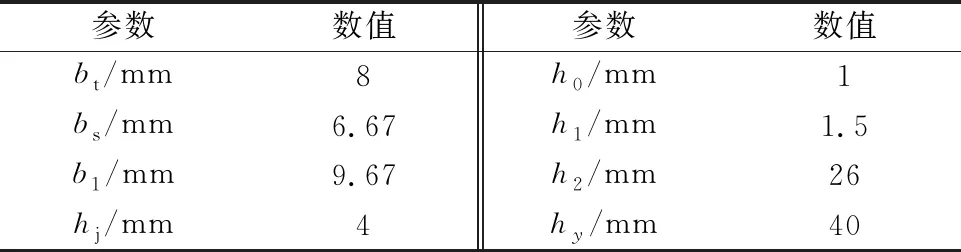
表3 PMSLM槽型尺寸

根据以上的设计参数，线圈全匝长和相电阻分别：

L=2lef+4de+2t

(19)

(20)

式中：de为端部绕组长度，取4 mm；ρ为电阻率，考虑电机额定负载时温度ρ=0.245×10-3Ω·mm2/cm。计算可得L=245 mm,Rs=4.8 Ω。

2.4 次级永磁体设计

次级所采用的永磁体牌号为N35，剩磁密度Br=1.23 T，相对磁导率μr=1.09。根据实际安装情况，取气隙长度δ=0.8 mm。取次级永磁体长度与铁心有效长度相等，即lm=lef，根据永磁旋转电机永磁体计算公式[8]可得，永磁体厚度hm=4.5 mm，宽度bm=14 mm。

3 有限元仿真分析

根据上述电磁设计得到的电机主要尺寸及参数进行二维有限元建模[9-10]仿真，仿真模型如图4所示。三相绕组按图2分布，A，C两相位于两端，B相绕组位于中间。以A相绕组中线为原点，使得A相绕组轴线与磁极d轴对齐。

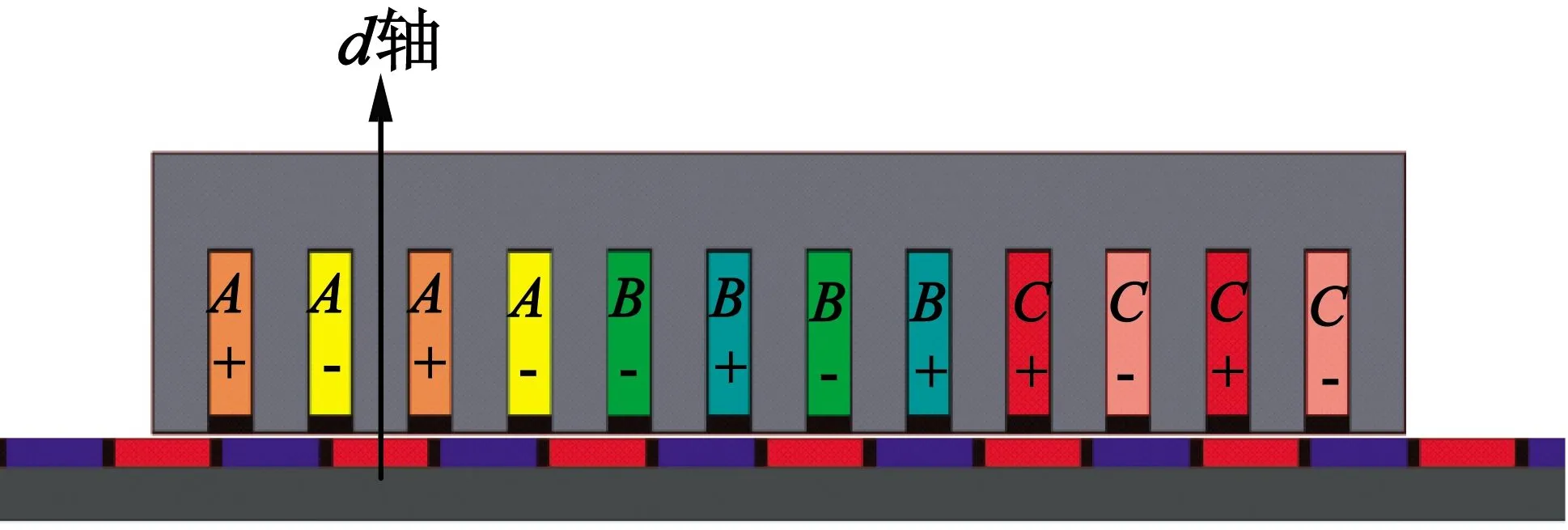
图4 PMSLM仿真模型

对于PMSLM通常采用斜极的方式来削弱推力波动。使用二维有限元分析斜极时，需通过将整体磁钢斜极等效为多段斜极结构，如图5所示。当分段数k很大时，可认为其与整体斜极等效。通过分段斜极将电机划分为k个子电机，通过二维有限元仿真得到各个子电机的推力和推力波动并求和，即可得到电机采用斜极后总的推力及推力波动。本文采用20段分段斜极，从以下的图9中可以看出，定位力中4次分量占比较大，通过斜极90°电角度来削弱4次推力波动分量。

(a) 分段斜极

(b) 整体斜极

3.1 空载仿真分析

PMSLM空载磁力线分布如图6所示。

从图6中可以看到，不同于旋转电机，由于直线电机的铁心断开，故两侧端部的磁力线产生畸变，从而产生了直线电机特有的端部力效应；此外，由于存在两个断开的端部，故三相绕组的分布不对称。

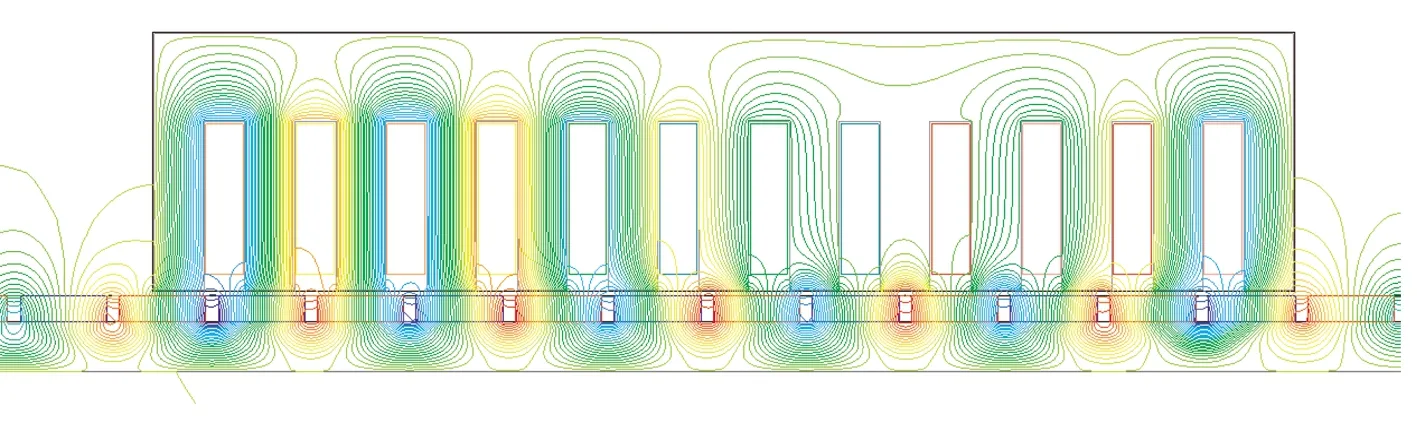
图6 PMSLM空载磁力线分布

图7为三相绕组的电感波形。从图7中可以看出，分布在两个端部A，C两相电感波形基本接近，而分布在中间的B相电感值虽然大于其他两相电感值，但是电感差值很小。

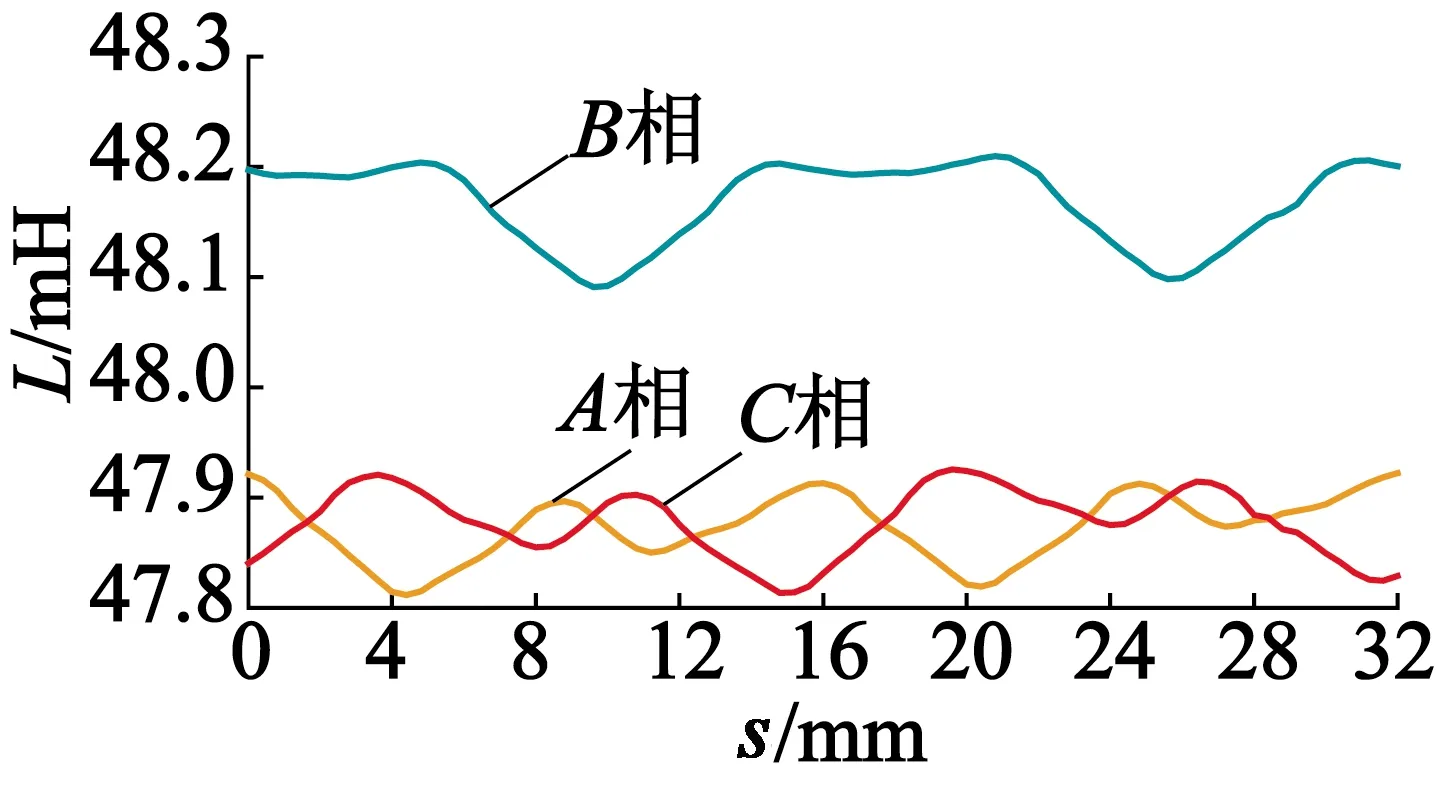
图7 PMSLM电感波形

如图8所示，由于采用了分数槽绕组结构，故空载反电动势的波形具有很好的正弦性，通过FFT分析可以看出，主要含有少量的3、5次谐波，而对于三相星形连接的绕组来说，3次谐波不会对电机性能产生影响。未斜槽空载反电动势基波幅值为238.76 V，斜槽后空载反电动势基波幅值为219.03 V，斜槽使得空载反电动势的相位发生变化，永磁体斜槽明显降低反电动势的基波幅有效值，但同时也削弱了3、5次谐波。

(a) 空载反电动势波形对比

(c) 斜槽FFT分析

虽然斜槽后反电动势幅值减小，但是斜槽结构使得电机的定位力大大削减，如图9所示。未斜槽定位力峰峰值为50.94 N, 斜槽后定位力峰峰值为13.78 N，定位力削减了73%，未斜槽时单个周期内定位力波动次数为4，斜槽时单个周期内定位力波动次数降为2。定位力是永磁直线电机的重要性能指标，在高精度定位驱动系统中直接影响系统的定位精度，在电机设计中应考虑尽可能减小定位力。

图9 PMSLM定位力波形对比

3.2 额定负载仿真分析

采用常用的最大推力/电流比控制方式控制电机电流，本文的电机不存在凸极，即凸极率为1，则最大推力/电流比控制就是实现id=0的控制。id=0电流控制下的永磁电机相量图如图10所示。此时，电流相位与空载反电动势相位重合，功角θ与功率因数角φ相等。

图10 id=0控制相量图

负载仿真采用三相对称电压源激励，给定额定速度v=3.2 m/s，通过调整电压源的初始相位角，最终实现电流与空载反电动势相位重合。负载仿真波形如图11所示，电流相位与空载反电动势相位完全重合，相电压与相电流相位相差φ=30.2°，则cosφ=0.864。相电流有效值I=4.2 A,相电压有效值U=220 V，负载反电动势有效值E=201 V,则1-εL=0.914。

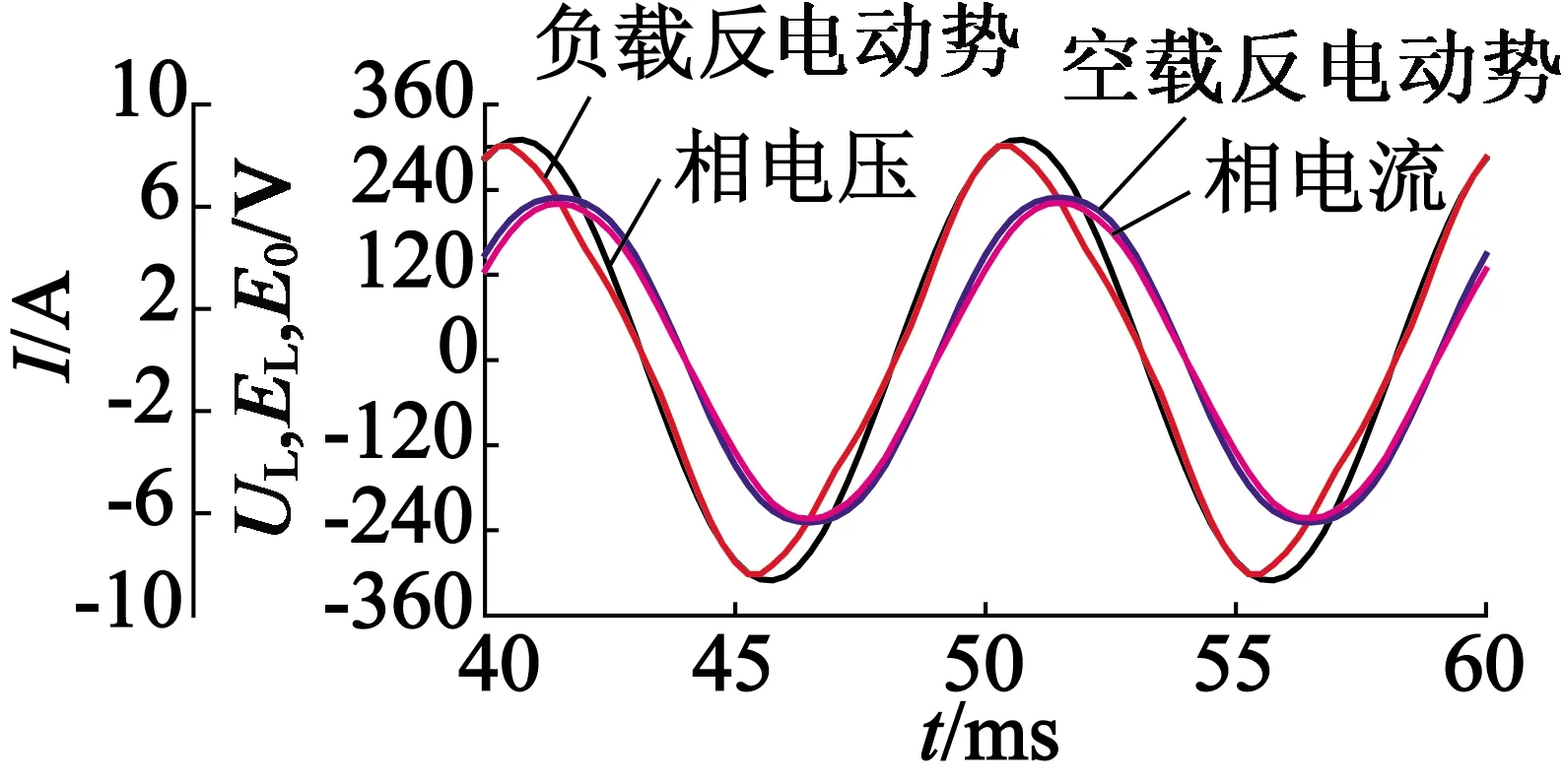
(a) 额定负载电流与电压波形

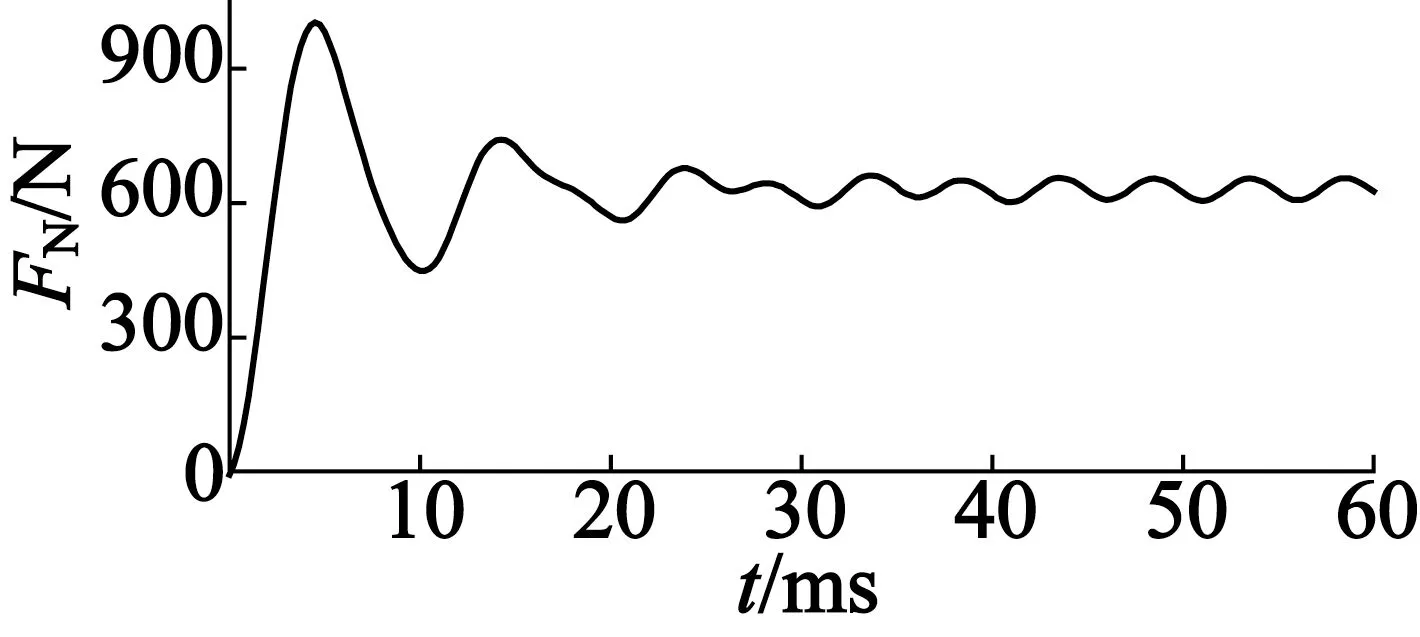
(b) 额定推力波形

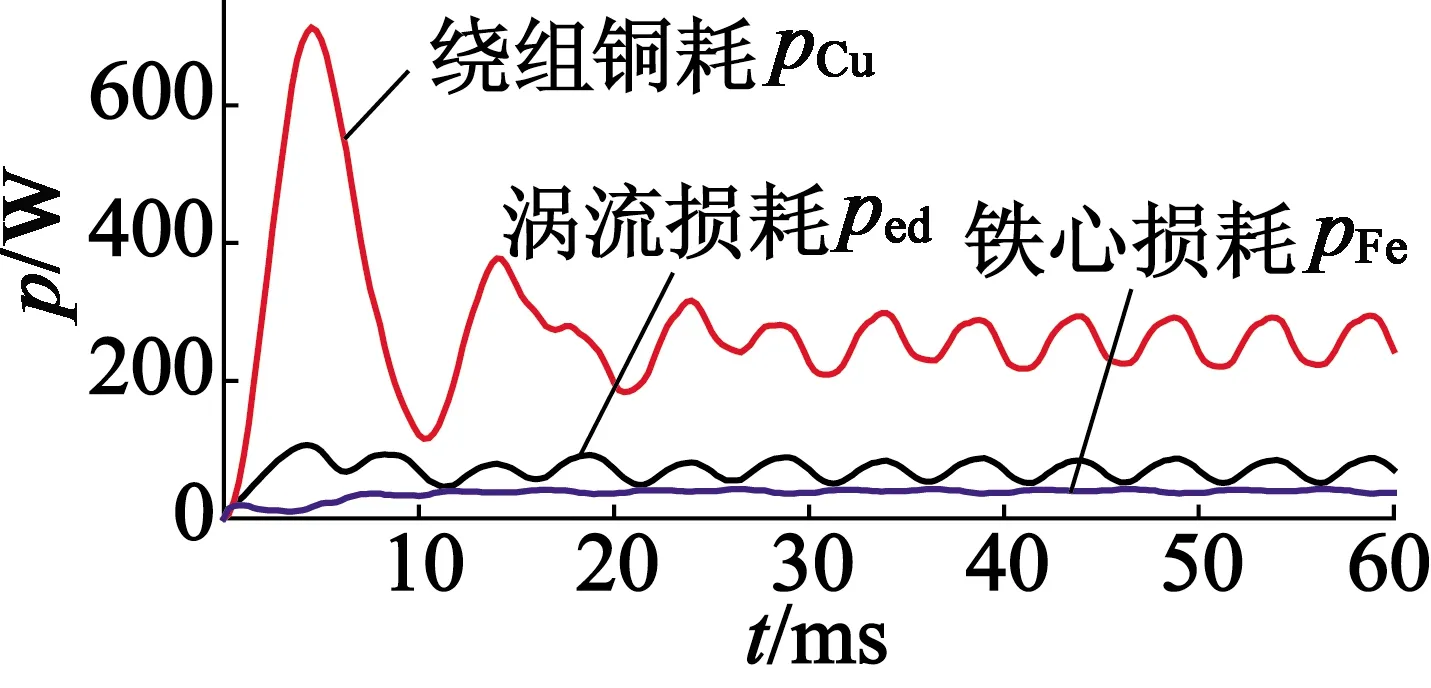
(c) 额定负载损耗波形

额定推力在4个周期后趋于稳定，稳定后的推力平均值FN=631 N,推力波动为8.1%。从损耗波形可以得出，绕组铜损PCu=254 W，铁心损耗pFe=40 W,永磁体和永磁轭板的涡流损耗ped=70 W，效率通过下式计算：

(22)

由式(22)计算得η=0.847。

4 结 语

本文首先给出了PMSLM的基本结构，然后以经典的旋转永磁电机电磁设计公式为基础，推导出了适合PMSLM的电磁设计公式，并确定了PMSLM的基本尺寸，最后建立二维有限元模型进行仿真分析。对比了空载运行时，斜极前后的定位力和反电势波形，电机额定状态下的仿真结果验证了电磁方案的可行性。研究结果对PMSLM工程设计和应用具有指导意义。