基于永磁体磁场的数值计算与仿真分析研究
兰州交通大学土木工程学院 杨禄权 孙子阳 周志奇
引言
随着新的永磁材料的应用领域不断扩大,人们对永磁体磁场的探讨更加关注。目前,对永磁材料磁场分布的研究方法有理论研究和实验研究。苟晓凡等人[1]根据分子环流模型和毕奥-萨伐尔定理,对仅在一个方向均匀、完全充磁的矩形永磁体,导出了一块及多块磁体按极性相反并列放置时的磁场解析表达式。李鑫等人[2]根据等效电流模型得出了永磁体位于坐标原点时的磁场分布。然而由理论研究方法所求得的结果往往缺少试验数据的验证,因此结果的正确性难以得到验证。宋浩等人[3]运用实验和COMSOL(“静磁场,无电流”的应用模式)模拟给出了相对放置的永磁条、具有磁回路结构的磁轭磁极、环形磁体的磁场分布。马俊等人[4]运用实验方法研究了不同辅助永磁体厚度的磁场分布。在理论研究中,常采用数值计算法和有限元法来计算永磁体的磁场强度,因此对于数值计算和有限元方法的研究是非常有必要的。
本文根据等效电流模型及安培分子环流定律,运用基于剩余磁通密度Br的Comsol multiphysics软件与基于面电流密度Js的Fortran程序分别研究了圆柱形永磁体与矩形永磁体的磁场分布,对比分析了永磁体剩余磁通密度Br与面电流密度Js的优越性。
1 永磁体模型的建立
1.1 Fortran计算原理
假设永磁体内部分布着密度为J的分子电流,外部分布着密度为Js的表面电流。如果磁介质整体匀称,则由同一性可知,在磁介质内的任意位置都存在着两个相邻的分子环流,由于它们拥有等大反向的电流,所以其磁场相互抵消,但截面边界处的分子电流不被抵消。因此,磁体上所有分子环流可等效为沿截面边界的环形电流,而无体电流。
根据安培分子环流定律可知:将永磁体视为无数个电流环组成,则空间任一点的磁场可认为是各个电流环分别在该点产生的磁场强度的叠加。建立柱坐标系(P,ф,Z),其简单模型如图1所示:
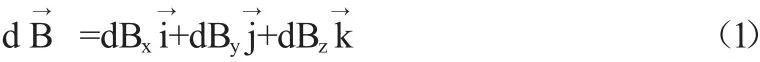
其中,dBx、dBy、dBz是电流环在P(x,y,z)处产生的磁场分别在x、y和z方向的分量。
根据毕奥-萨伐尔定律:

这里μ0=4π×10-7牛顿/安培2,为真空磁导率。
则永磁体对空间任一点P(x,y,z)产生的磁场为:
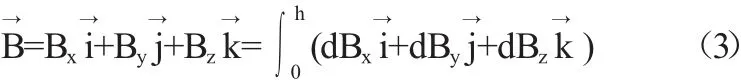
其中,h为永磁体的高度。
已知永磁体的磁场计算公式,可以采用精度较高且较常用的Simpson积分法进行求解。在Fortran的积分命令流中,通过重复调用Simpson积分命令来实现磁场的计算。则采用复化Simpson求积公式计算定积分:

将区间[a,b]逐次分半,令

则复化Simpson求积公式为:

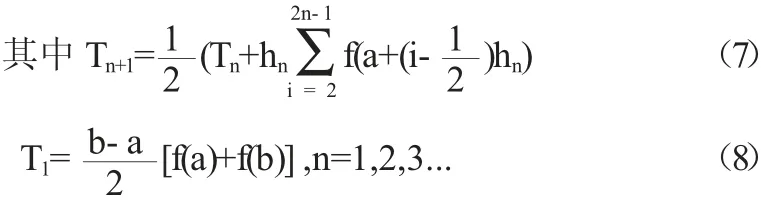
在计算二重积分时,数值积分的处理办法为:

根据永磁体的磁场公式以及Simpson积分法编制Fortran程序求解永磁体的磁场强度。其中,积分精度为10-6,积分子程序允许的最大步数为20。
1.2 Comsol multiphysics计算原理
Comsol multiphysics软件是一款专业的有限元数值分析软件,在仿真永磁体的磁场强度时,通过Comsol multiphysics软件的AC/DC模块下的“磁场,无电流”物理场求解。外部环境设定为:温度T=293.15K,绝对压强Pa=Iatm,由于静磁场中没有电流的存在,因此可以使用标量磁势的方法来解决。由公式H=-△Vm和△*B=0就可以求出磁铁周围的磁场分布。
由上述Fortran的计算原理可知,若已知永磁体的等效电流密度J8,则永磁体的剩余磁通密度为:

其中,Br为剩余磁通密度,真空磁导率μ0=4π×10-7,为面电流密度。
则剩余磁通密度与磁场之间的本构关系为:

2 结果讨论与分析
根据上述永磁体的磁场计算原理,运用Fortran程序和Comsol multiphysics软件分别计算圆柱形永磁体和矩形永磁体的磁场强度,并与实验结果作对比,分析讨论基于两种不同软件计算永磁体的磁场强度时,永磁体的剩余磁通密度和面电流密度的优越性。
2.1 基于圆柱形永磁体的结果分析
首先,我们采用In-Gann Chen et al.(1992)实验[5]中圆柱形永磁体的参数:RPM=9.525mm,HPM=6.35mm,JS=7820A/cm进行数值模拟与仿真计算,得到永磁体表面(霍尔探头距永磁体表面的最小距离为1mm)横向磁场Bz的空间分布。
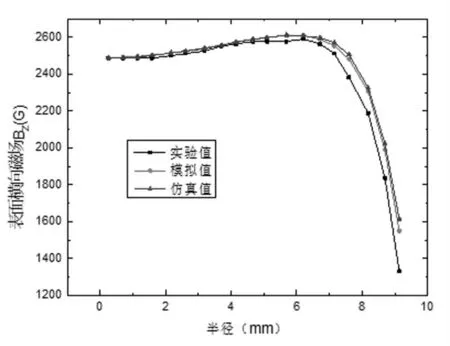
图2 永磁体横向磁场分布图
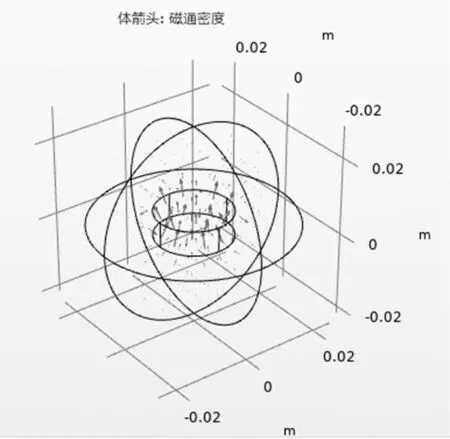
图3 圆柱形永磁体磁场强度空间体箭头
图2 为圆柱形永磁体横向磁场分布,可以看出:圆柱形永磁体磁场的模拟结果、仿真结果及实验结果吻合很好,表明计算程序以及Comsol multiphysics软件仿真计算的可靠性。图3为圆柱形永磁体的磁场强度空间体箭头分布,可以看出:磁感应线从圆柱形永磁体的N极出发闭合回到S极,不仅证明了磁通连续性原理也充分验证了等效电流模型计算的正确性。
将计算结果与In-Gann Chen et al.(1992)实验的数据作对比,其对比数据如下表1所示:
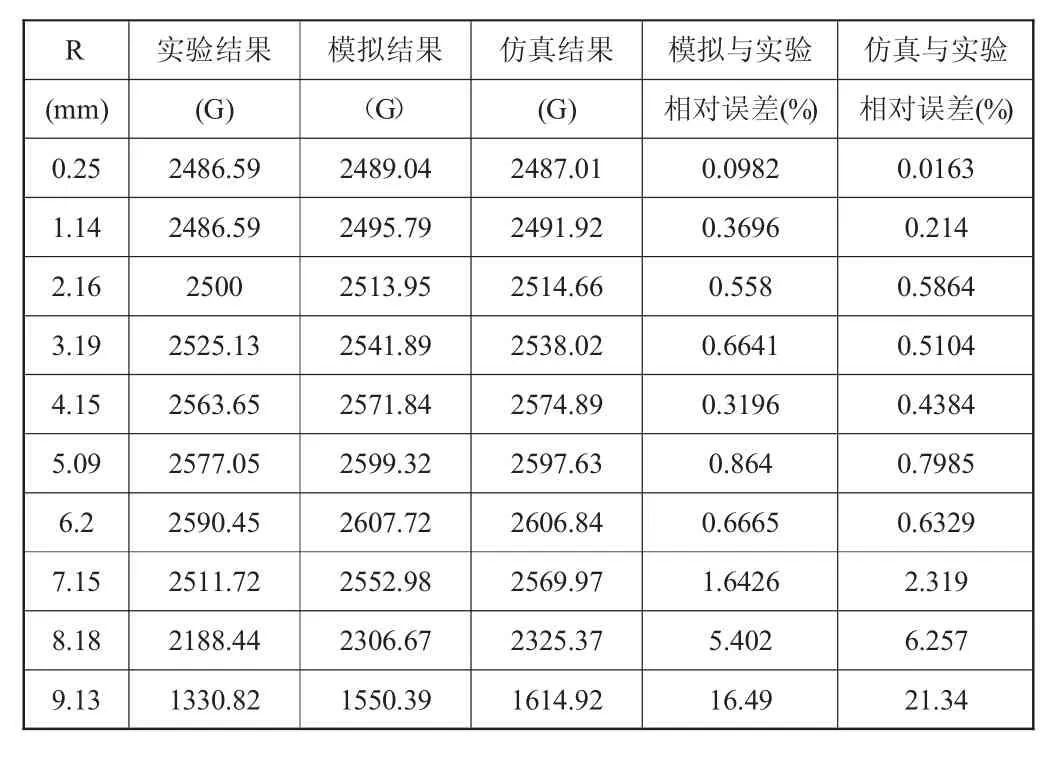
表1 圆柱形永磁体表面横向磁场
表1 为圆柱形永磁体的横向磁场的实验结果分别与模拟结果和仿真结果对比分析表,从中可知:模拟结果与实验结果的相对误差很小,平均相对误差为2.30%;仿真结果与实验结果的相对误差也很小,平均相对误差为2.77%。但是仿真结果与实验结果的相对误差平均值较大于模拟结果与实验结果的相对误差平均值。
2.2 基于矩形永磁体的结果分析
这里,我们采用刘宏娟[6]论文里的实验中矩形永磁体的参数:长度a=50mm,宽度b=10mm,高度h=5mm,面电流密度Js=4πk(其中k=49677.11A/m)进行数值模拟与仿真计算,得到永磁体表面(距永磁体表面60mm)中心部位的横向磁场Hz随宽度的空间分布,将模拟结果与仿真结果与刘宏娟论文里的实验数据作对比,其对比数据如下表2所示:

表2 矩形永磁体表面横向磁场
表2 为矩形永磁体的横向磁场的实验结果分别与模拟结果和仿真结果的对比分析表,从中可知:模拟结果与实验结果的相对误差很小,平均相对误差为-3.57%;仿真结果与实验结果的相对误差也很小,平均相对误差为5.17%。但是仿真结果与实验结果的相对误差平均值较大于模拟结果与实验结果的相对误差平均值。
3 结论
本文基于Fortarn程序和Comsol multiphysics软件分别探讨了圆柱形永磁体与矩形永磁体的横向磁场分布,并与实验结果作对比,通过分析两种模型的模拟结果和仿真结果与实验结果的相对误差,讨论了永磁体剩余磁通密度Br与面电流密度Js的优越性。结论如下:
(1)本文首先给出了Fortran程序与Comsol multiphysics软件计算的两种永磁体磁场强度的计算方法,并给出了两种方法之间的联系。
(2)基于永磁体面电流密度Js的磁场强度的模拟结果的相对误差小于基于永磁体剩余磁通密度Br的磁场强度的相对误差,表明永磁体基于面电流密度Js的磁场强度比基于剩余磁通密度的磁场强度更可靠。

