基于绝热温升方法的饱和铁心损耗分布分析

胡蔡飞，童力，范学良，袁银男，郑宏，黄镠

（1.苏州大学轨道交通学院，江苏 苏州 215000；2.国网浙江省电力有限公司电力科学研究院，杭州 310014；3.柯林电气股份有限公司，杭州 310011；4.国网丽水供电公司，丽水 323000）

0 引言

叠片铁心结构被广泛应用于电机、变压器等电气设备，铁心损耗是电气设备功率损耗的主要来源，其准确的预测和计算对设备的电磁和热管理设计具有重要指导意义[1-3]。

磁滞效应和集肤效应等物理现象导致铁心损耗的非线性变化。此外，根据不同的工作原理和几何结构，不同设备铁心损耗的计算存在较大差异。变压器运行过程中，由于直流偏磁的存在[4]，叠片铁心逐渐趋于饱和，励磁电流发生畸变[5-6]；电机铁心损耗的计算需要考虑磁场的旋转[7-10]；电抗器特殊的磁阀结构使得铁心周期性的进入深度饱和，铁心损耗非线性程度大。因此，叠片铁心损耗的计算模型难以完整考虑所有因素对损耗的影响。

工程上通常使用损耗模型法来计算铁心损耗，常用的损耗计算公式为Bertotti损耗三项式和Steinmetz公式等。为计算非正弦激励下的铁心损耗，文献[11]采用变系数法对斯坦梅茨公式进行改进，建立考虑直流偏磁的铁心损耗模型。文献[12]则对Bertotti损耗三项式进行优化，以此建立铁心损耗模型，用于计算正弦及谐波激励下的铁心损耗。文献[13]基于Bertotti损耗模型，给出了一种能够考虑畸变磁通影响的谐波磁损耗工程计算方法。

上述文献中所提出的叠片铁心损耗计算方法和模型虽然可以较准确地计算出铁心损耗，但是均需建立在叠片铁心几何结构规则和损耗分布均匀的基础上。对于计算几何结构特殊（磁阀结构）和损耗分布不均匀的叠片铁心损耗是不适用的，需要在已有的叠片铁心损耗模型基础上做出修正以得到特殊结构铁心损耗的计算模型。而铁心损耗的准确测算是对铁心损耗模型进行正确修正的根本前提。

铁心损耗作为叠片铁心的热源，使得铁心温度随时间变化[14-15]。因此，使用测得的叠片铁心温度来逆推叠片铁心损耗的方法受到越来越多的关注。文献[16-17]使用热成像技术对变压器叠片铁心的温度变化进行采集，通过对所得温升曲线数据进行处理计算出叠片铁心损耗分布。文献[18]使用反演分析法建立简单几何结构感应电动机的温度逆模型，最终计算出感应电动机铁心损耗分布。

电抗器由于特殊的工作原理，其铁心存在磁阀结构，磁阀结构所引起的损耗分布不均匀制约着铁心损耗的正确计算[19-24]。有磁阀铁心是典型的特殊结构铁心，因此将有磁阀铁心作为实验和分析对象更具代表性和实际意义[25-28]。本文在已有研究的基础上，提出基于绝热温升法的饱和叠片铁心损耗计算方法。首先对无磁阀结构的饱和叠片铁心使用本文所述方法，所得损耗值和文献[29]所提出方法的结果比较，证明本方法的正确性。再将本文所述方法应用于有磁阀的饱和叠片铁心，计算出此特殊结构铁心的损耗分布。实验结果表明，本文所提方法不受叠片铁心几何结构、损耗分布影响，损耗计算较准确，可为特殊结构铁心损耗模型的修正提供理论和实验基础，对功率设备的电磁和热管理设计具有指导作用，有较大的应用前景。

1 饱和铁心等效模型和仿真

图1所示为传统铁损测量设备的结构图。铁心上紧密缠绕两个线圈，初级线圈匝数NL，次级线圈匝数NR，NL=NR。初级线圈连接电压激励，初级线圈上电流i和次级线圈电压uR可测得。之所以设置次级线圈，是因为初级线圈上有电流，从而引起电压降，使得初始线圈电压uL难以准确测量。次级线圈上未连接任何负载，因此不会产生电压降，其两端电压uR可以正确测量。

图1 铁心损耗测量装置结构图Fig.1 Structural diagram of iron-core loss measurement device

图1 所述铁损测量装置可等效为如图2所示的电路。

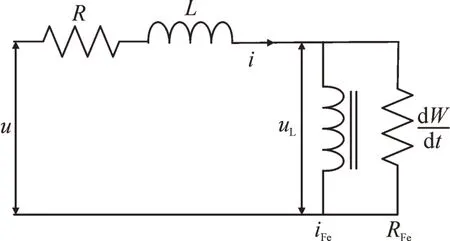
图2 等效电路Fig.2 Equivalent circuit

图中u为绕组两端输入电压，uL为铁心两端电压，R为绕组及串联电阻，L为绕组漏感，i为绕组上电流，iFe为磁化电流，RFe为涡流损耗等效电阻，W为磁链。可得到回路电压方程为

根据基尔霍夫电流定律和全电流定律可得公式

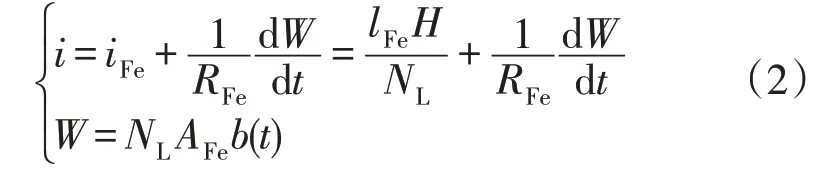
式中：lFe为铁心等效磁路长度。

涡流损耗等效电阻值RFe可表示为[19]

式中：d为单片电工钢厚度；σ为电工钢电导率。已知单位质量铁心损耗PFe（W/kg）公式为

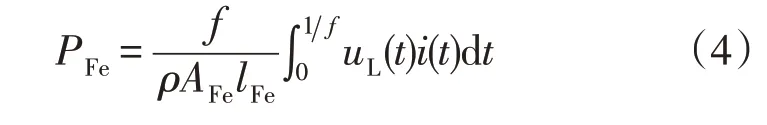
式中：AFe为铁心横截面积，mm2；ρ为铁心所使用电工钢的密度，kg/m3；f为电压频率，Hz。

电压和磁感应强度关系可表示为

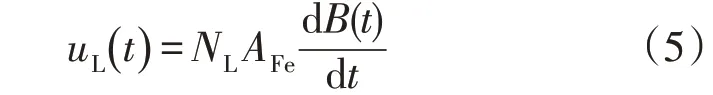
联立（2）-（5）可将单位质量铁心损耗公式变形为

可见铁心损耗由磁滞损耗和涡流损耗两部分组成。

在Simulink中建立饱和铁心仿真。本文所述实验输入电压u，R=25Ω。电流iFe由可控电流源产生，仿真得到电压uL（t），磁感应强度B（t）可由下式计算得到。

磁场强度H（t）由B-H曲线经由插值得到，将所得磁感应强度和磁场强度代入式（5）计算得到铁心损耗。得到的损耗值用来与绝对温升法得到的损耗值对比，检验绝热温升法方法的正确性。

2 绝热温升法铁心损耗计算模型和实验

2.1 绝热温升法铁心损耗计算模型

为实现特殊结构的饱和叠片铁心损耗的计算，本节建立绝热温升法铁心损耗计算模型。饱和铁心单位质量损耗PFe（W/kg）作为热源，可得饱和铁心三维非稳态导热微分方程，公式为

式中：ρ为铁心所使用电工钢的密度，kg/m3；c为定压比热容，J/（kg·K）；T为铁心温度，K；t为温升时间，s；A为铁心表面积，m2。

铁心z方向上薄层之间绝缘层热阻较大，可认为z方向上不进行热传导（kz=0）；又因为测温点布置于中心位置且远离铁心边缘和损耗剧烈变化的区域，可认为∂T/∂x=0，∂T/∂y=0。

单位时间内因对流而损失的热量由牛顿冷却公式描述为

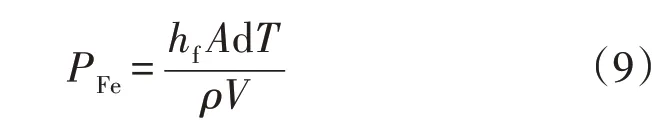
式中：hf为传热系数，W/（m2·K）；V为铁心体积，m3。

考虑饱和铁心处于绝热状态，hf=0，此时铁心损耗完全作用于铁心温度的升高，得到公式为

对于本文所述饱和铁心测温实验，铁心热源同时包含铁心损耗和线圈交流电阻损耗。式（9）改写为

式中，PR为单位质量线圈交流电阻损耗，W/kg。

实验电压频率为50 Hz，计算得集肤深度（21 mm）远大于所用导线直径（1 mm），可认为交流电阻值等于直流电阻值，给出线圈交流电阻损耗公式为

式中：I为线圈交流电流有效值；R为线圈直流电阻值。可得饱和铁心损耗计算公式为

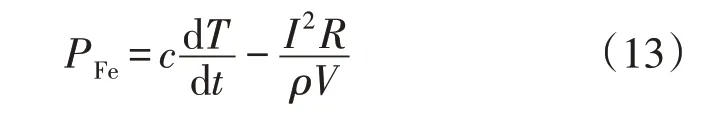
对于构造规则均匀的饱和铁心，计算出多点的损耗值，再求出其平均损耗，即为饱和铁心损耗值。而对于构造不规则的饱和铁心，可以测得多点的损耗值，进而得到该结构不规则饱和铁心的损耗分布。

2.2 实验装置和参数

实验所用铁心由50 WW470型无取向电工钢堆叠而成，铁心和电工钢具体参数见表1，50 WW470型无取向电工钢的B-H曲线见图3，更多材料属性可在文献[20]中得到。

表1 铁心和电工钢具体参数Table 1 Specific parameters of core and electrical steel

图3 无取向电工钢B-H曲线Fig.3 B-H curve of non-oriented electrical steel

首先在铁心上布置所需的光纤测温探头。然后在铁心四柱紧密均匀缠绕导线，导线直径1 mm，并用石棉紧密包裹使得铁心和外界绝热。在绕组接头串接水泥电阻和调压器（型号T15101931，额定输出电压0～300 V）。光纤测温探头连接荧光光纤温度解调仪，最后传输实时温度信息至计算机，进行温度数据采集和处理。实验所用荧光光纤温度解调仪型号为FOTC-MX06A-06020-N，测温范围：-50～+200℃，测温精度：±0.3～0.5℃。光纤温度探头型号为FOTP-GB2-02M-ST-N，探头直径：2.2 mm，测温范围：-200～+200℃，测温精度：±0.5℃。实验电气参数见表2。

表2 电气参数Table 2 Electrical parameters

铁心实物图见图4，图4（a）为无绕组铁心，图4（b）为有绕组铁心。

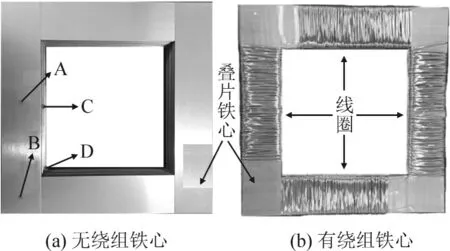
图4 叠片铁心实物图Fig.4 Physical drawing of laminated iron core

3 方法验证和应用

3.1 方法验证

各电压下线圈电流波形见图5。由电流波形可知，当电压从75 V增加到125 V时，其总谐波畸变率（THD）由38.5%增大为53%，电流畸变加大，这表明铁心在电压为75 V时已经进入饱和，在电压为125 V时达到较深的饱和度。

图5 各输入电压下线圈电流波形Fig.5 Current waveform of coil at various input voltages

各电压下绕组电流有效值可由示波器测量得出，具体数值见表3。

表3 电流有效值Table 3 RMS of current

不同电压下，饱和铁心损耗值见图6。

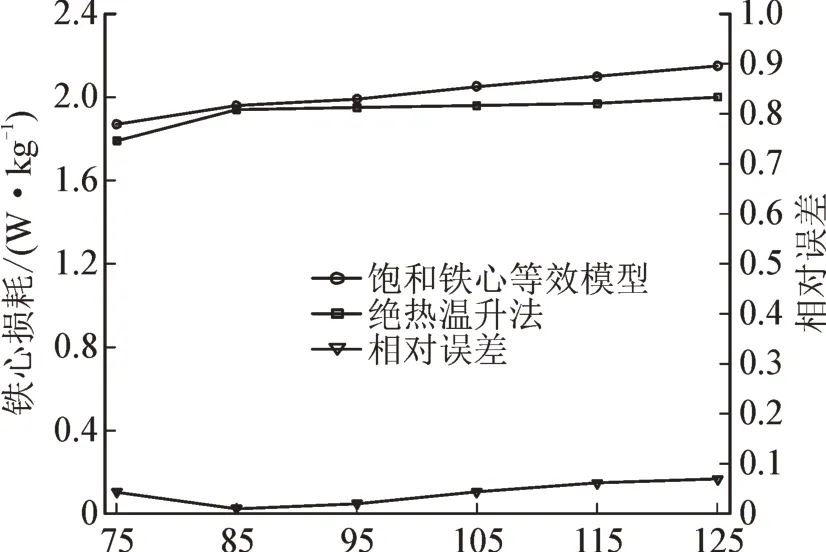
图6 饱和铁心损耗Fig.6 Loss of saturated core

图6中分别给出了使用1.2所述饱和铁心等效模型计算的损耗值以及使用本文所述绝热温升法所得出的饱和铁心损耗值以及相对误差。

由结果可知，绝热温升法得到的饱和铁心损耗值略小于饱和铁心等效模型中得到的饱和铁心损耗值，这是因为实验无法做到完全绝热，导致计算结果略小于实际值。但是两者相对误差较小，电压125 V时，相对误差最大为7%，电压85 V时，相对误差最小，为1%。因此可以认为本文所提出的基于绝热温升的饱和铁心损耗计算方法是正确且可行的。电压为75 V时，铁心尚未达到深度饱和，损耗值为1.79 W/kg，电压为85 V时，铁心达到深度饱和，损耗值为1.94 W/kg，损耗增加较明显（9%）。当电压大于85 V时，铁心均处在深度饱和，损耗持续增加。

3.2 实验结果分析

实验中得到各个电压下，测温探头测得的饱和铁心上各点绝对温升实时曲线，实验时长5 000 s，见图7。

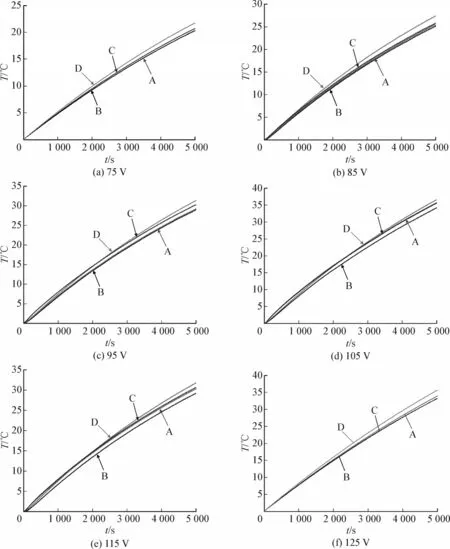
图7 各电压下饱和铁心温升曲线Fig.7 Temperature rise curve of saturated core at various voltages

图中A、B、C、D 4个测温点温升曲线对应深浅颜色。以测温点A为例，电压75 V，时间5 000 s时，A点绝对温升为20.3℃；电压125 V，时间5 000 s时，A点绝对温升为39℃，绝对温升随电压增大而增大。由绝对温升可计算得到温度梯度，5 000 s时刻，不同电压下各测温点绝对温升见表4。

表4 不同电压下各测温点绝对温升Table 4 Absolute temperature rise of each temperature measuring point under various voltages ℃

由图7和表4可知，位于铁心表面的测温点A和B绝对温升曲线趋于一致，且最大绝对温升值相差较小（0.4℃），可见铁心表面各点绝对温升大致相同，即铁心表面损耗大致相等。测温点C和D都位于铁心内部，有所区别的是测温点C处在铁心柱中间内部，测温点D处在铁心柱接头处内部。由结果可知，测温点C处绝对温升与表面测温点A、B相差较小，而测温点D处绝对温升曲线与A、B、C 3个测温点相差较大，5 000 s时D点绝对温升比A、B、C绝对温升平均大1℃。可见铁心表面及铁心柱内部损耗分度均匀，但铁心柱接头处内部损耗略高。

综上所述，本文所提出的损耗计算方法，不仅可以较为准确地计算出饱和铁心的损耗值，而且可以进一步分析饱和铁心损耗的分布情况，这是饱和铁心等效模型无法实现的。

3.3 绝热温升方法应用

在前文实验使用的传统铁心验证本文所述方法正确性的基础上，进一步将本文温度计算方法应用到带有磁阀结构的饱和铁心上。本节使用的有磁阀铁心是在前文铁心基础上增加一个宽度为20 mm，长度为40 mm的磁阀结构，磁阀是常见于可控电抗器的一种调节铁心饱和度的结构，此外的其他结构参数与前文铁心结构完全相同，线圈阻值5Ω，有磁阀铁心见图8。

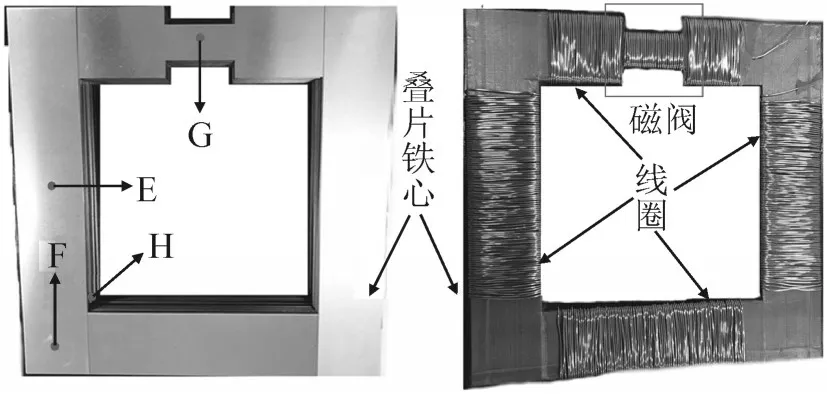
图8 有磁阀叠片铁心Fig.8 Laminated core with magnetic valve

实验得到有磁阀铁心在各电压下电流波形，图9是电压为75 V时传统铁心和有磁阀铁心的电流。

图9 电流波形图Fig.9 Current waveform

通过对比可以发现，磁阀结构的存在使得相等电压值下电流畸变更大，铁心饱和程度更深，线圈所得电压75 V时电流有效值为0.7 A。使用本文所述损耗计算方法得出测温点E、F、G、H（见图8）在不同电压下的损耗值，分析其损耗值和损耗分布情况，计算结果见图10。

图10 有磁阀饱和铁心损耗Fig.10 Iron loss of saturated core with magnetic valve

由图10可看出，测温点F损耗最小，为0.66 W/kg，测温点H处损耗最高，为1.56 W/kg，损耗最大处值是损耗最小处值的2.4倍；测温点E、G处损耗均较高。这是因为测温点G和测温点E均位于铁心中心位置，且都被线圈包裹，两点所处位置磁感应强度较大，损耗大。测温点H位于铁心拐角处边缘，此处漏磁现象严重，涡流损耗大。测温点F位于铁心拐角处中心位置，此处距离边缘较远，漏磁较小，并且场强均匀，导致总体损耗较小。有磁阀饱和铁心损耗分布与3.1节所述传统铁心损耗分布相比，有磁阀铁心的损耗分布比较不规则。

对于有磁阀铁心或者其他结构不均匀的铁心而言，损耗分布也不均匀，导致饱和铁心等效模型损耗计算难以应用于此。而本文所提出的损耗计算方法不受铁心结构和损耗分布的影响，只要将测温点布置在合适的位置，便可以计算出饱和铁心损耗分布。

4 结语

本文提出了一种基于绝热温升法的饱和铁心损耗计算方法。试验方法得出的传统饱和铁心损耗值与饱和铁心等效模型损耗值进行比较，结果表明本文提出的方法切实可行。在此基础上，使用本文提出的损耗就计算方法对有磁阀饱和铁心损耗进行计算，成功得到有磁阀饱和铁心损耗。总结本文所述损耗计算方法的实验结果，本文提出的基于绝热温升法饱和铁心损耗计算方法不仅是正确合理的，而且适用性广，不局限于铁心的构造是否规则均匀。此外，还可得到饱和铁心损耗的具体分布，这对铁心的结构优化、相关设备的电磁和热管理设计具有重要指导作用。