非线性连续体拓扑优化方法综述1)
文桂林 刘 杰 陈梓杰 魏 鹏 龙 凯 王洪鑫 荣见华 谢亿民
* (燕山大学机械工程学院,河北秦皇岛 066004)
† (广州大学机械与电气工程学院,广州 510006)
** (华南理工大学土木与交通学院,广州 510641)
†† (华北电力大学新能源学院,北京 102206)
***(长沙理工大学汽车与机械工程学院,长沙 410076)
††† (皇家墨尔本理工大学创新结构与材料研究中心,澳大利亚墨尔本 3001)
引言
连续体拓扑优化是指在给定边界条件、载荷,以及各种约束条件下,根据性能指标要求,通过严格的数学理论得到结构最优材料布局的过程[1-3].它可以从力学上根本提升结构机械性能,其本质上属于无穷维空间中变系数微分方程的0~1 控制问题,被公认为是最具挑战性的结构优化问题.近年来,连续体拓扑优化在工程领域也展现出巨大发展潜力,已经在航空航天、海洋工程、机械工程等多个工程领域发挥了重要作用.图1(a)~图1(h)给出了连续体拓扑优化方法的典型工程应用.

图1 连续体拓扑优化方法的典型工程应用: (a) 卫星支撑系统[4];(b) 海上风力发电机组导管架支撑结构[5];(c) 机翼结构[6];(d) 飞机扰流板[7];(e) 超长悬索桥[8];(f) 导弹气动设计[9];(g) 飞机蒙皮拉伸成形模具[10];(h) 空客A320 机舱铰链支架[11]Fig.1 Typical engineering application of continuum topology optimization method: (a) satellite support system[4];(b) offshore wind turbine jacket support structure[5];(c) wing structure[6];(d) aircraft spoiler[7];(e) super-long suspension bridge[8];(f) missile aerodynamic design[9];(g) drawing die for aircraft skin[10];(h) hinge bracket of Airbus A320 cabin[11]
均匀化方法开创了连续体拓扑优化的先河[12],其思想是将设计区域离散为大量单元,通过微孔结构几何参数来确定单元的有无.由于具有设计变量多、优化最终构型为多孔结构导致难以制造等缺点,限制了其发展和应用,但是,其理论基础严谨,且目前在材料设计领域还持续展现出活力[13-15].继均匀化法之后,连续体拓扑优化方法得到了快速的发展,逐渐形成了变密度法,包括固体各向同性材料微结构/插值惩罚法(solid isotropic macrostructure/material with penalization method,SIMP)[16-17]和材料性能的合理近似法(rational approximation of material properties,RAMP)[18]、渐进结构优化方法(evolutionary structural optimization,ESO)[19-21]、水平集法(level set,LS)[22-24]、独立-连续-映射法[25-26]、特征驱动法[27-28]、相场法[29-30]、拓扑导数法[31]以及移动可变形组件/空洞法[32-34]等.这些方法各有优缺点,共同促进了连续体拓扑优化领域的蓬勃发展.图2给出了典型的连续体拓扑优化方法设计一个二维悬臂梁的最终构型对比图,可见,各种方法均可产生清晰的拓扑构型.

图2 悬臂梁设计问题及不同拓扑优化方法的优化型Fig.2 Cantilever design problem and optimization with different topology optimization methods
变密度法、渐进结构优化方法和独立-连续-映射法由于采用像素点描述结构构型,会有结构边界不光滑的问题.此外,变密度法会产生灰度单元,这些都增加了实际制造难度,不过可以通过细分单元、使用新的过滤策略等方式进行缓解.比如,文桂林团队[35-36]提出了结构边界单元自适应策略和积木博弈策略,有效地缓解了BESO (bi-directional evolutionary structural optimization,BESO)方法和SIMP 方法中结构边界不光滑的问题,降低了后处理时边界经验处理带来的误差.变密度法发展较早,相对于其他方法在理论层面上较为成熟;而谢亿民团队[19-21]提出的渐进结构优化方法具有算法理念简单、收敛速度快和边界清晰等优点,且成功开发了商用软件Ameba,已在建筑工程、机械工程和航空航天等领域的创新设计方面展现出来强大的实际工程解决能力[37].水平集法、特征驱动法、相场法、拓扑导数法和移动可变形组件/空洞法属于基于边界演化发展的拓扑优化方法,这类方法的优势在于能够得到光滑和清晰的优化结构边界,且几何信息可以通过函数表示,易于提取最终构型的几何信息;然而,由于计算通常基于固定的有限元网格,动响应和灵敏度的计算精度方面有一定的提升空间.张卫红团队[27-28]提出的特征驱动拓扑优化方法将结构特征贯穿于结构建模、分析和优化设计的整个流程,即,将CAD 特征模型嵌入到结构拓扑模型,从源头上保证了结构的特征属性.郭旭团队[32-34]提出的移动可变形组件/空洞法给出了一种显式的水平集演化模式,大幅度地减少了设计变量的数目,提高了计算效率,且优化结果可与CAD 软件进行直接连接,易于制造.此外,作为LS 法的一种,参数化水平集方法可以改善传统水平集方法的初始设计依赖性缺陷,然而,由于材料分布不存在中间密度,材料密度突变易造成不连续的拓扑变化,致使优化过程不稳定.基于此,Wei 等[38]结合变密度法的优势,提出了水平集带方法.该方法的思路是,利用具有一定宽度的水平集带范围替代传统零水平集面,水平集带区域内的材料密度通过插值可以连续地分布于[0,1]范围内.
目前连续体拓扑优化在解决线性问题中发展较为成熟,已经成功解决了诸如传热、增材制造、振动抑制、稳健性和可靠性设计等问题[39-50].然而,实际工程中存在大量的非线性问题,若近似为线性问题来解决,会导致较大的误差,甚至是错误的结果.实际结构设计中的非线性主要体现为三种: 材料非线性、几何非线性和边界非线性(接触非线性).图3 分别为三种非线性问题的示意图.图3(a)为材料非线性问题,其中材料的应力应变之间不再是线性关系,常见的如弹塑性、超弹性等;图3(b)为几何非线性问题,当结构发生几何大变形、大挠度或大转动时,力和位移曲线不再是线性关系,即刚度矩阵不再是常数;图3(c)为边界非线性问题,结构边界在分析过程发生变化.基于此,本文将分别对材料非线性、几何非线性和边界非线性三种连续体拓扑优化方法进行综述.需要指明的是,本文重点在宏观力学范畴内对非线性连续体拓扑优化进行综述,对于考虑微观结构的非线性拓扑优化问题可以参考文献[51].

图3 三种结构非线性Fig.3 Three kinds of structural nonlinearity
1 材料非线性连续体拓扑优化
材料非线性主要体现为材料应力-应变关系的非线性,在实际工程中比较常见的非线性材料为弹塑性材料和超弹性材料.当弹塑性材料受力变形导致内部应力超过比例极限时,其应力-应变将呈现非线性关系,随着应力水平的进一步提升,当应力超过屈服应力时,将产生不可恢复的塑性变形.而超弹性材料具有更为复杂的非线性应力-应变关系,在大变形状态下卸载可恢复初始状态.如何将不同类型非线性材料的应力-应变关系引入到拓扑优化列式,以及求解由此为计算带来的系列难题,是材料非线性连续体拓扑优化区别于线性问题的关键.本部分将以弹塑性材料和超弹性材料两个类别对材料非线性连续体拓扑优化相关研究进行综述.
1.1 弹塑性材料连续体拓扑优化
Maute 等[52-53]较早地在SIMP 法框架下,利用Von Mises 应力屈服准则推导了弹塑性材料塑性部分的非线性应力-应变关系,其中需要分别建立弹塑性材料的杨氏模量、硬化模量和屈服应力的插值模型,然后将塑性部分与弹性部分相结合,得到弹塑性材料的应力-应变关系,该方法需要权衡三种插值模型的惩罚系数,见图4(a).在此基础上,Wallin 等[54]发展了弹塑性结构能量吸收最大化的拓扑优化方法,见图4(b);Kato 等[55]研究了体积约束下弹塑性复合材料能量吸收能力最大化的拓扑优化方法,见图4(c);Li 等[56-57]提出了抗断裂的吸能弹塑性结构拓扑优化设计和循环荷载作用下的耗能弹塑性结构拓扑优化设计方法,见图4(d);Blachowski 等[58]研究了应力约束下弹塑性结构拓扑优化新方法.弹塑性材料模型可简化为由杨氏模量、硬化模量和屈服应力确定的双线性应力-应变形式,杨氏模量和硬化模量分别为第一线性段和第二线性段的斜率,屈服应力作为两个线性段的分段应力值.但是,同样需要分别建立三个相关材料属性的插值模型.以此为基础,Mayer 等[59]和Patel 等[60]研究了弹塑性材料拓扑优化设计在吸能方面的应用;Guimarães 等[61]将拓扑优化应用在采用血管成形术的支架细胞设计中;Lee 等[62]采用等效静载荷法高效地解决了非线性拓扑优化设计问题;Yoon 等[63]发展了一种单元连接参数化方法,为弹塑性材料拓扑优化设计提供了一种新的有效思路,但是该方法也会增加额外的刚度矩阵计算,一定程度上牺牲了计算效率,见图4(e);豆麟龙等[64]发展了一种基于渐进结构优化方法的弹塑性材料拓扑优化设计方法;Luo 等[65]提出了一种移动等值面阈值法,解决了弹塑性材料的拓扑优化设计问题,该方法允许删除的孔洞单元参与设计变量的更新,并在随后的迭代中重新出现,因此,具有相对较高的计算精度;Kongwat 等[66]发展了基于比例法的弹塑性材料拓扑优化方法.此外,在均匀化法框架下,Yuge 等[67]建立了一个材料张量的二维数据库,以解决弹塑性材料拓扑优化问题.Bogomolny等[68]采用Drucker-Prager 屈服准则建立弹塑性模型,提出了一种针对钢筋混凝土结构的概念设计新方法.以最大损伤为约束,Li 等[69]提出了一种结构最优能量吸收的拓扑优化方法;随后,基于非局部弹塑性损伤模型,他们发展了结构抗破坏拓扑优化方法,所采用的非局部弹塑性损伤模型通过Von Mises 应力屈服准则与一个非局部损伤函数耦合实现[70],见图4(f).Zhao 等[71]通过构造一个虚构的非线性弹性模型,并利用渐近分析的方法考虑满足Von Mises 应力屈服准则的非线性材料响应,并以此建立了两类优化列式,即应变能最大化和载荷系数最大化,见图4(g).此外,徐斌团队近期在BESO 框架下,发展了考虑应力约束的材料非线性拓扑优化方法[72-73].需要指出,除了具有非线性应力-应变关系,加载路径相关性是弹塑性材料连续体拓扑优化的另一个特点.该特点导致求解优化目标函数和约束函数对设计变量的灵敏度信息变得困难,其敏度分析过程需采用考虑路径相关的伴随求解策略.可见,弹塑性材料连续体拓扑优化相关研究中,通常采用Von Mises 应力屈服准则推导弹塑性材料塑性部分的非线性应力-应变关系,也有一些研究使用简化的双线性模型.对于一些更加复杂的问题,可对Von Mises 应力屈服准则塑性材料模型进行进一步修正.
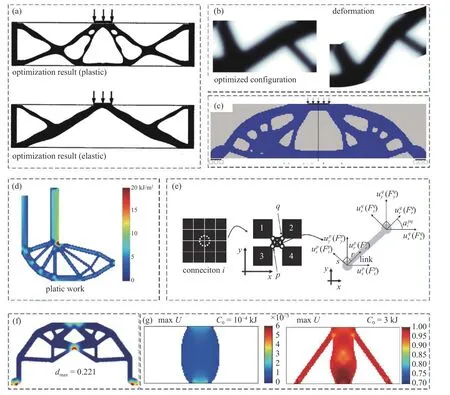
图4 弹塑性非线性拓扑优化: (a) 弹塑性和弹性拓扑优化设计简支梁结构对比[52];(b) 有限塑性变形最大塑性应变能最大化设计[54];(c) 弹塑性吸能最大简支梁结构优化设计[55];(d) 抗断裂吸能L 型结构设计[56];(e) 单元连接参数化策略示意图[63];(f) 抗材料损伤能量吸收结构优化设计[70];(g) 考虑应变能最大和载荷系数最大的材料非线性拓扑优化设计[71]Fig.4 Elastoplastic nonlinear topology optimization: (a) comparison between elastoplastic and elastic topology optimization design of a simply supported beam structure[52];(b) maximum plastic strain energy design with finite plastic deformation[54];(c) optimal design of a simply supported beam structure with maximum elastic-plastic energy absorption[55];(d) design of a fracture resistant and energy absorbing L-shaped structure[56];(e) schematic diagram of element connection parameterization strategy[63];(f) optimal design of energy absorbing structure resistant to material damage[70];(g) nonlinear topology optimization design of materials considering maximum strain energy and maximum load coefficient[71]
1.2 超弹性材料连续体拓扑优化
相对于弹塑性材料模型,超弹性材料具有更为复杂的应力-应变关系,通常采用应变能函数描述其本构关系[74],比较经典的包括Mooney-Rivlin 模型、Neo-Hookean 模型、Kirchhoff-St.Venant 模型和Ogden 模型等.本部分根据本构模型分类综述超弹性材料连续体拓扑优化方法.需要指出的是,超弹性行为往往包含了几何非线性,关于几何非线性拓扑优化相关问题和研究进展见第2 部分.
基于Mooney-Rivlin 模型,Lee 等[75]对考虑静动态特性的橡胶隔振器进行拓扑优化设计,见图5(a);文献[76-77]在水平集方法框架下研究了考虑几何非线性的超弹结构拓扑优化方法,见图5(b);Deng 等[78]认为在设计大变形超弹性材料时,Von Mises 应力破坏准则不准确,进而提出一种基于畸变能的连续体拓扑优化方法(见图5(c)),其中在低密度区域,利用了Wang 等[79]提出的应变能插值方法;Ortigosa 等[80-81]解决了SIMP 和LS 框架下超弹性材料大应变拓扑优化设计中算法不稳定问题;薛日野等[82]推广了移动可变形空洞法,实现了超弹结构拓扑优化设计,见图5(d).利用Neo-Hookean 模型表征超弹本构模型,基于多凸本构模型与松弛函数法,Lahuerta 等[83]实现了超弹结构的几何非线性拓扑优化,该方法在优化过程中无需去除孔洞单元,具有较高计算精度;James 等[84]将连续体拓扑优化方法应用到超弹性双稳态心血管支架的优化设计,见图5(e);充分利用无网格法解决大变形问题,Zhang 等[85]提出了一种有限元法与无网格伽辽金法结合的超弹结构拓扑优化方法,见图5(f);Wallin 等[86]研究了在几何非线性拓扑优化中使用割线刚度和切线刚度对最终优化构型的影响,研究发现,在低荷载水平下,两种结构构型差别不大,而在大变形情况下,则存在显著差异;受附加超弹材料技术的启发[87],张宪民团队[88]发展了与商业化软件ANSYS 结合的超弹结构几何非线性拓扑优化方法,并提供了MATLAB 程序,良好地提升了几何非线性拓扑优化方法应用实际工程结构设计的能力,见图5(g);在此基础上,Ye 等[89]在ICM 框架下,解决了应力约束的非线性拓扑优化设计.然而,该方法在解决三维非线性问题时会存在不收敛的问题,基于此,受文献[87-88]启发,文桂林团队[90]近期发展了一种基于多分辨率框架的超弹材料拓扑优化设计方法,用单核PC 机成功解决了千万分辨率的三维非线性结构优化设计问题,该方法具有高效和保精度的优点,并可以很好地解决三维非线性问题,见图5(h);Capasso 等[91]提出了应力约束下的柔性机构非线性拓扑优化方法;Zhang 等[92]改进了BESO方法,解决了发生大变形的超弹材料设计问题,见图5(i).基于Kirchhoff-St.Venant 模型,Bruns 等[93-94]提出了一种适定的考虑几何大变形的连续体拓扑优化数学模型,解决了结构非线性拓扑优化设计问题,并应用到柔性机构设计;Klarbring 等[95]研究了包含非零位移约束下的超弹结构拓扑优化问题,对比了多种超弹性材料模型对最终拓扑材料分布的影响,发现基于Kirchhoff-St.Venant 模型所得的优化构型与其他包含物理压缩行为的模型有所差异,且力学性能较差;基于变密度法、水平集法和扩展有限元法,Geiss 等[96]发展了一种可以优化设计大变形4D 打印结构的有效方法.然而,对于有些实际具体工程问题,需要对经典超弹性材料本构模型进行修正.Luo 等[97]研究了在无摩擦接触支承下超弹结构的拓扑优化问题,其中超弹性材料的应变能函数通过人工惩罚模型表示.为了考虑超弹性材料的非线性,Chi 等[98]在SIMP 法框架中提出一种改进的Ogden通用本构模型,该模型可同时考虑平面应变和平面应力两种情况,并通过改变材料参数能够使材料在平面应变和平面应力情况下获得一定范围的非线性材料行为.综上所述,超弹性材料具有十分复杂的应力-应变关系,对于基于有限单元法的连续体拓扑优化的优化列式建立、灵敏度推导以及算法稳定性都是一个挑战.另外,在实际工程问题中,只通过单轴拉伸试验往往无法得到足够的样本点来表征超弹材料行为,与经典本构模型有较大误差,需要同时开展单轴试验、双轴试验、平面试验、体积试验等.
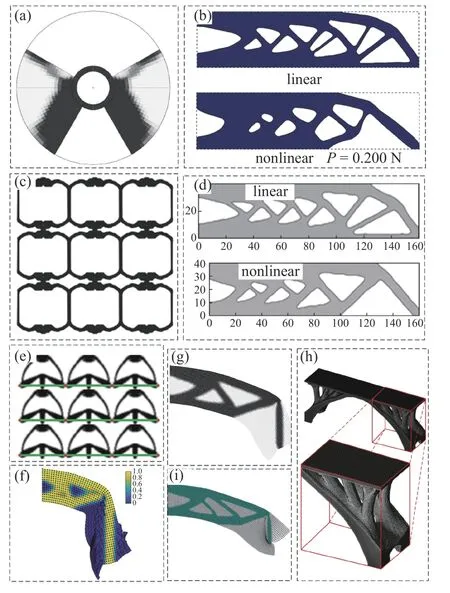
图5 超弹性材料拓扑优化: (a) 橡胶隔震器拓扑优化[75];(b) 水平集法线性和非线性优化设计悬臂梁结果对比[77];(c) 基于畸变能的拓扑优化设计[78];(d) 基于移动可变形孔洞方法设计悬臂梁结构[82];(e) 双稳态心血管支架优化设计[84];(f) 有限元和无网格耦合拓扑优化方法设计悬臂梁结构[85];(g) 柔性机构几何非线性设计[88];(h) 高分辨率三维非线性拓扑优化设计类桥梁结构[90];(i) 改进的BESO方法优化设计悬臂梁结构[92]Fig.5 Topology optimization of hyperelastic materials: (a) topology optimization of rubber isolator[75];(b) comparison of linear and nonlinear optimization design of a cantilever by level set method[77];(c) topology optimization design based on distortion energy[78];(d) design of a cantilever structure based on MMV method[82];(e) optimal design of a bistable cardiovascular stent[84];(f) design of a cantilever structure by finite element and meshless coupling topology optimization method[85];(g) geometric nonlinear design of a flexible mechanism[88];(h) high resolution 3D nonlinear topology optimization design of bridge structure[90];(i) optimization design of a cantilever structure by improved BESO method[92]
2 几何非线性连续体拓扑优化
对使用过程中会发生大位移或大转动的工程结构进行连续体拓扑优化设计时,需考虑几何非线性的影响.几何非线性连续体拓扑优化问题中,有限元响应求解的刚度矩阵具有位移相关性,常采用Newton-Raphson 迭代求解其非线性平衡方程.基于变密度法的几何非线性连续体拓扑优化中,中低密度单元区域刚度较低,当结构发生大变形时,这些材料区域易发生过度畸形,致使Newton-Raphson 迭代中的切线刚度矩阵失去其正定性质,无法求解非线性平衡方程,进而导致非线性拓扑优化无法收敛.而其他经典拓扑优化方法与变密度法类似,空洞区域的低刚度同样会带来数值求解困难.若将结构中除实体单元外的其他单元统称为“伪材料”单元,几何非线性连续体拓扑优化的难题主要在于如何解决单元过度畸形导致的数值不稳定.几何非线性包括大位移小应变和大位移大应变两种情况,前者称为弱几何非线性,而后者称为强几何非线性.目前关于几何非线性连续体拓扑优化的相关研究大部分针对弱几何非线性情况,若无特别说明,本文默认指弱几何非线性情况.本部分分别基于“伪材料”单元、单元畸形和切线刚度矩阵非正定这三个特征对几何非线性连续体拓扑优化相关研究进行综述.
2.1 基于排除“伪材料”单元思路的几何非线性连续体拓扑优化
在拓扑优化迭代循环过程中人为地将“伪材料”单元排除在外,可以有效避免非线性有限元计算失败.基于这一思想,Buhl 等[99]认为低密度单元节点位移的持续振荡是导致Newton-Raphson 迭代无法收敛的原因,他们在SIMP 法框架中提出“收敛准则松弛”法,将被低密度单元包围的节点排除在Newton-Raphson 迭代过程的收敛准则之外,见图6(a).随后将该方法应用于大位移柔性机构拓扑优化设计[100],研究发现,与线性拓扑优化构型相比,考虑几何非线性拓扑优化构型的输出性能增益可达2.5 倍.基于该思路,李兆坤等[101]实现了多输入多输出的柔性机构几何非线性拓扑优化设计,见图6(b);在参数化水平集框架下,Luo 等[102]进一步将该思想推广到求解大位移柔性机构拓扑优化问题;为了解决几何缺陷对结构稳定性的影响,Jansen 等[103]推广了文献[99] 的“收敛准则松弛”法,发展了一种稳健性拓扑优化方法.基于SIMP 法,Bruns 等[104]提出一种“单元移除法”,该方法可将删除的低密度单元重新引入的策略,根据迭代历史中单元密度是否低于所规定密度这一规则对单元进行计数,若该单元在此次迭代中密度小于所规定密度,则次数减1,反之加1,并通过单元次数与所设定阈值的比较判断是否对单元状态进行切换,见图6(c).借鉴“单元移除法”,Luo 等[65]利用移动等值面设置阈值,低密度单元在有限元计算中被消除,而在计算结构响应时被重新引入.Cho 等[105]认为外力的加载方式带来较多“伪材料”单元导致优化过程不容易收敛,因此,他们采用了位移加载方式来缓解该问题.基于无网格法,Cho 等[106]通过重构核形状函数对位移场和体密度场进行离散,使形状控制点能够位于设计域任何部分,这种做法可将低密度域排除在有限元响应分析之外,解决了几何非线性拓扑优化数值求解数值不稳定问题,见图6(d);在SIMP 法框架下,Du等[107]利用无网格伽辽金法将单元设计域转化为节点设计域,发展了一种新的几何非线性拓扑优化方法,并应用于大位移柔性机构优化设计,该方法由于不需要单元进行插值,可避免中低密度区域单元过度畸变问题;在水平集法框架下,Yamada 等[108]提出了一种利用粒子交互模型结合移动粒子半隐式思路,成功解决了几何非线性拓扑优化数值困难;基于无网格伽辽金法,亢战团队[109]提出了一种独立密度场插值的几何非线性拓扑优化方法,该方法采用了能量收敛准则,有效解决了由于低密度局部数值不稳定带来的收敛困难.此外,在BESO 框架下,Huang等[110-112]系统地研究了位移荷载和力载荷作用下几何非线性拓扑优化问题,见图6(e).值得提出的是,徐斌团队近年来在BESO 框架下,进一步发展了几何非线性拓扑优化方法,成功解决了应力约束等问题[113-114].此外,张卫红团队[115]提出了一种考虑连接点载荷约束和几何非线性的装配体结构拓扑优化设计方法,他们采用超单元压缩方法对低刚度区域自由度进行压缩,以避免算法不收敛问题.

图6 基于排除“伪材料”单元思路的几何非线性拓扑优化: (a) “收敛准则松弛”思路(白色单元四周的节点被排除)[99];(b) 多输入多输出柔顺机构优化设计[101];(c) 使用“单元移除法”前后设计柔性结构构型对比[104];(d) 基于无网格法进行悬臂梁设计[106];(e) 基于BESO 的几何非线性拓扑优化设计[111]Fig.6 Geometrically nonlinear topology optimization based on eliminating "pseudo material" elements: (a) "convergence criterion relaxation" idea (nodes around white elements are excluded)[99];(b) optimal design of a multi input and multi output compliant mechanism[101];(c) comparison of flexible structure configuration before and after using "element removal method"[104];(d) design of a cantilever based on meshless method[106];(e) geometrically nonlinear topology optimization based on BESO[111]
综上所述,“收敛准则松弛”法发展较早,且思想简便,应用较为广泛,但其为了实现数值稳定性,直接忽略了低密度单元的有限元响应,导致最终优化结果精度不高.“单元移除法”直接将单元进行移除,同样影响优化结果精度,而低密度单元在有限元计算中被消除,在计算结构响应时被重新引入的策略可以一定程度提高计算精度.考虑到低密度单元数值不稳定出现在非线性有限元求解环节,而并非拓扑优化环节,无网格分析技术提供了另一种有效的手段,具有较高精度,但存在计算量大、效率较低等缺点.
2.2 基于改变单元畸形思路的几何非线性连续体拓扑优化
解决几何非线性连续体拓扑优化数值不稳定性的另一个思路是将单元的过度变形转化为其他方式体现或者对单元变形进行缩放,以抑制单元过度畸形.基于这一思想,Yoon 等[116-117]利用单元连接参数化法分别在SIMP 和水平集法框架下进行了几何非线性拓扑优化设计,见图7(a)和图7(b).单元连接参数化法使用零长度一维弹性连杆连接相邻单元,利用弹性连杆变形代替平面单元变形,由于平面单元保留了原始材料特性,可在结构发生较大变形时避免过度畸变.弹性连杆的存在表示相邻单元的连接,最终保留优化迭代结束时相互连接的单元,这种方法称为外部单元连接参数化方法,与之对应,他们后来又发展了内部单元连接参数化方法,并扩展到基频优化问题[118-119].在此思想基础上,Moon 等[120]发展了单元连接参数化qp 松弛法,以解决Von Mises 应力约束下的体积最小化几何非线性拓扑优化设计问题.在水平集法框架下,利用Delaunay三角剖分技术,Ha 等[76]提出了一种网格重划方法,并采用超弹性材料,一定程度上避免了由于大应变引起的单元内部过度变形.此外,网格局部细化策略[35]也可以一定程度上缓解几何非线性拓扑优化过程中的单元过度扭曲问题.van Dijk 等[121]基于SIMP 法提出了单元变形缩放技术,将单元的节点位移分离成保留的旋转刚体部分和允许缩放的变形部分,根据单元密度大小对其内部单元位移进行插值实现单元变形缩放,从而避免低密度单元过度畸形,见图7(c).
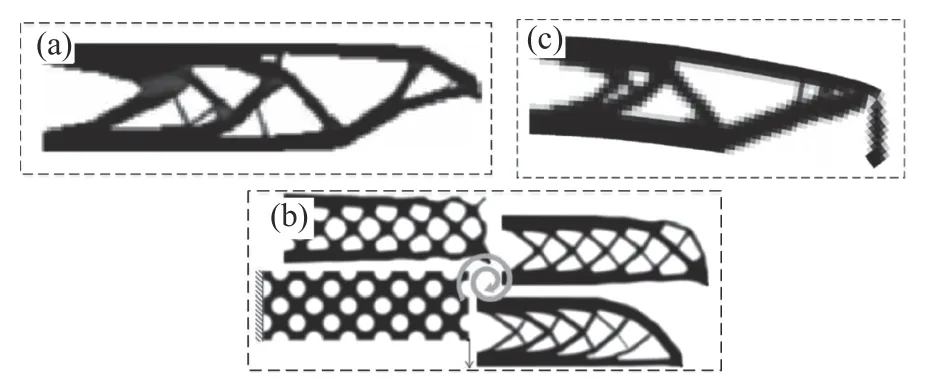
图7 基于改变单元畸形思路的几何非线性拓扑优化: (a) 单元连接参数化法在SIMP 框架下悬臂梁设计[116];(b) 单元连接参数化法在水平集框架下悬臂梁设计[117];(c) 利用单元变形缩放技术进行悬臂梁设计[121]Fig.7 Geometrically nonlinear topology optimization based on the idea of changing element deformity: (a) designing a cantilever under SIMP framework by element connection parameterization method[116];(b)design of a cantilever under level set frame by element connection parameterization method[117];(c) cantilever design using the element deformation scaling technology[121]
由此可见,基于改变单元畸形思路的几何非线性连续体拓扑优化方法可以一定程度上缓解优化过程中的数值不稳定难题,但在计算效率和计算精度上仍需要进一步的提升.单元连接参数化方法在几何非线性拓扑优化问题求解中展现出了良好的潜能,但亦存在额外的刚度矩阵计算导致其计算效率较低等问题.网格重划分和局部网格细化策略可以一定程度缓解数值不稳定难题,但是较难从根本上解决.单元变形缩放技术中单元内力对外部位移场比较敏感,致使其处理几何非线性拓扑优化问题时有一定的局限性.
2.3 直接影响切线刚度矩阵非正定的几何非线性连续体拓扑优化
直接影响切线刚度矩阵非正定特性是另一种解决几何非线性连续体拓扑优化数值不稳定的思路.Bruns 等[94]建议额外添加超弹性材料防止单元过度畸形导致的数值收敛困难.在多材料多输出大位移柔性机构拓扑优化设计中,Saxena[122]利用遗传算法隐式地规避计算非线性变形时的不收敛解问题,见图8(a).Cho 等[123]在水平集法框架下,采用均匀材料属性和隐式边界转换为显式边界的策略实现了几何非线性求解的数值稳定性.Kawamoto[124]利用Levenberg-Marquardt 法替代Newton-Raphson法对非线性方程进行迭代求解,避免了优化迭代过程中的不收敛问题,见图8(b).基于等效静载荷思路,Lee 等[62]将非线性静态响应近似等效为某一些时刻静载荷的线性静态响应,有效解决了几何非线性连续体拓扑优化设计问题.为了保证切线刚度矩阵的正定性,Lahuerta 等[83,125]采用多凸性本构模型结合松弛函数实现了过度变形单元的稳定.Yoo 等[126]使用改进的蚁群优化算法实现了几何非线性拓扑优化.Gomes 等[127]将序列分段线性规划算法引入到几何大变形结构拓扑优化问题求解.Wang 等[79]基于SIMP 法提出一种新的能量插值策略,在低刚度单元区域和实体单元区域分别采用小变形理论和大变形理论对弹性能密度进行插值,保证了切线刚度矩阵正定性.后来,Lazarov 等[128]将该方法应用到微机电系统的大位移柔性机构的稳健性拓扑优化设计.Wallin 等[86]比较了使用割线刚度和切线刚度对最终优化构型的影响,他们发现,当结构发生小变形时,最终构型基本一致,而当发生大变形时,则会出现明显的区别.Zhu 等[129]发展了移动可变形组件法,成功解决了几何非线性拓扑优化问题,见图8(c);Silva 等[130]提出考虑应力约束、制造不确定性和几何非线性的柔性机构拓扑优化方法;Zhu 等[131]使用开源软件平台FreeFEM 编写了几何非线性拓扑优化MATLAB 程序.在SIMP 法框架下,Luo 等[87]提出附加超弹材料技术,在中低密度区域中加入一种与原始单元共用节点的超弹性单元,通过所附加超弹性材料的高体积模量和剪切能力可以有效地缓解中低密度单元畸形导致的数值失稳问题.基于附加超弹材料技术,Chen 等[88]公布了几何非线性结构拓扑优化MATLAB 程序,将几何非线性拓扑优化算法与商业分析软件ANSYS 结合,一定程度上推进了拓扑优化算法的工程实用性.在此基础上,龙凯等[132]提出了一种控制结构最大位移的几何非线性拓扑优化方法,具有良好的工程实用性,见图8(d).为了进一步提高优化结果的精度,Liu 等[133]提出了一种改进的附加超弹性技术,并实现了大位移柔性机构的几何非线性拓扑优化设计,见图8(e).此外,Dunning[134]提出一种基于共旋转法的几何非线性拓扑优化方法,这种方法的优点在于切线刚度矩阵具有固有正定性,见图8(f).需要指出的是,柔性机构一般利用几何大变形来实现大的位移或力传递,其拓扑优化需要考虑几何非线性,然而也应考虑诸如多输入多输出需求、类铰链、灰度单元等问题[2].比如,荣见华团队[135]近期提出了一种考虑多输入多输出的无铰链全解耦柔性机构拓扑优化的新方法以解决上述问题,可将该方法进一步推广到考虑几何非线性拓扑优化设计问题.
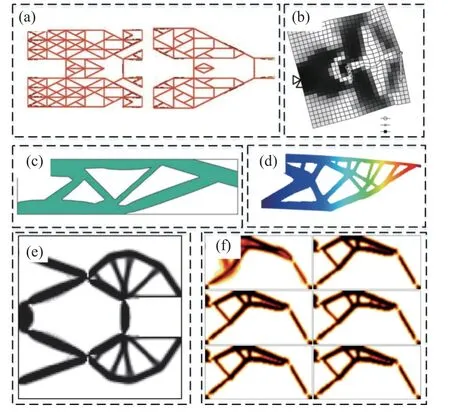
图8 基于直接影响切线刚度矩阵非正定思路的几何非线性拓扑优化: (a) 利用遗传算法优化大位移柔性机构[122];(b) 基于Levenberg-Marquardt 法优化直线运动机构[124];(c) 基于MMC 的悬臂梁优化[129];(d) 控制最大位移的悬臂梁设计[132];(e) 改进的附加超弹性技术优化设计柔性夹持机构[133];(f) 共旋转优化设计不同的位移反向器[134]Fig.8 Geometrically nonlinear topology optimization based on the idea of directly affecting the non positive definite tangent stiffness matrix:(a) optimization of a large displacement flexible mechanism using genetic algorithm[122];(b) optimization of a linear motion mechanism based on Levenberg-Marquardt method[124];(c) optimization of a cantilever based on MMC method[129];(d) design of a cantilever to control maximum displacement[132];(e) optimization design of a flexible clamping mechanism based on improved additional hyperelasticity technology[133];(f) optimal design of different inverter mechanisms with co-rotational method[134]
综上所述,上述方法可以有效影响切线刚度矩阵非正定特性,进而一定程度上缓解几何非线性拓扑优化数值不稳定问题,但是,也存在进一步改进的空间.比如,能量插值策略在低密度单元区域的线性有限元分析会一定程度上影响最终优化结果的精度;附加超弹材料技术额外地增加超弹性单元同样会影响优化结果的精度,且关键参数的经验选取对最终结果有一定的影响;Levenberg-Marquardt 法的实用性取决于迭代过程中启发式更新方案的选择;序列分段线性规划算法需要较多的计算成本;共旋转法由于需要进行额外的矩阵转换计算,计算效率较低.需要指出的是,基于排除“伪材料”单元和基于改变单元畸形思路来解决几何非线性拓扑优化数值不稳定问题的核心还是为了解决非线性有限元计算过程中切线刚度矩阵非正定问题,所以,上述三种策略在本质上是一样的.
3 边界非线性连续体拓扑优化
实际工程结构系统中,各结构之间往往发生接触,接触体的变形和接触边界的摩擦使得部分边界条件伴随加载过程而发生非线性变化,诸如此类结构拓扑优化设计需要考虑边界非线性.边界非线性一般发生在具有接触边界条件的结构变形问题中,如汽车碰撞、齿轮的啮合、电机组合转子的组装和轴承接触等.本部分对边界非线性连续体拓扑优化相关研究进行综述.
通过将次梯度优化算法引入到拓扑优化中,Petersson 等[136]优化了单边接触条件下板结构,使其刚度最大,该方法具有较好的收敛性和较高的计算效率,见图9(a).Mankame 等[137-138]借助正则化接触模型对辅助接触式柔性机构进行了拓扑优化设计,正则化接触模型利用平滑逼近的单边位移约束处理接触相互作用;后来,针对具有给定非光滑路径的辅助接触式柔性机构,他们提出了一种考虑大变形的正则化法向接触模型顺序优化方法,以克服该机构的非光滑响应求解难题,见图9(b).在接触边界条件下,Fancello[139]研究了考虑局部失效的质量最小多工况拓扑优化问题,在每个迭代步和加载工况下采用接触求解器以获得平衡变形构型.为了研究考虑结构件相互接触时的拓扑优化设计问题,Peng 等[140]在给出接触模型求解算法的基础上,建立含有接触约束的拓扑优化列式.Desmorat[141]利用均匀热力学势的概念,引入接触模型,建立了无摩擦单边接触柔度最小化的拓扑优化列式,并通过固定网格和局部灵敏度计算策略进行有效求解,见图9(c).为了求得具有给定摩擦的单边接触弹性体拓扑优化问题的数值解,Myśliński[142-143]利用控制位移场的二阶椭圆型变分不等式描述考虑摩擦的接触问题,并通过拓扑导数和水平集法进行求解,见图9(d).在SIMP 框架下,Strömberg 等[144]开展了无摩擦单边刚性支座接触的连续体拓扑优化问题,其中,利用增广拉格朗日法和光滑近似方法对Signorini 接触条件进行改进,以描述无摩擦接触问题.随后,为了提高该方法的计算效率,Strömberg[145]提出了一种以最大势能为目标的优化列式.他还进一步将该思想扩展到解决具有制造约束和单边接触约束的结构连续体拓扑优化问题[146],见图9(e).基于线性等效载荷法思路,Yi 等[147]发展了考虑接触非线性的连续体拓扑优化方法.基于显式水平集法和扩展有限元法,在无限小应变和线弹性假设下,Lawry 等[148]提出了一种解决弹性体之间存在滑移接触的连续体拓扑优化方法,见图9(f);在此基础上,他们又将该方法扩展到解决有限应变问题[149],见图9(g).利用材料掩膜覆盖策略,Kumar等[150-151]对考虑自接触和相互接触两种工况的柔性机构进行了拓扑优化设计.基于他们前面提出的附加超弹材料技术[87],并通过建立非线性弹簧模型模拟无摩擦接触支承,Luo 等[97]进一步研究了无摩擦接触支承下超弹结构的拓扑优化设计问题,研究发现,超弹结构发生大变形将导致结构的接触边界条件改变.针对无摩擦单边接触条件下结构刚度最大拓扑优化问题,Kanno[152]从拉格朗日对偶理论角度出发,建立了一种新的优化列式.基于三场SIMP 模型,通过引入接触压力方差约束,Niu 等[153]发展了一种无摩擦接触弹性结构的拓扑优化方法,该方法可提高接触压力均匀性,见图9(h).在假设接触区域已知的前提下,Kristiansen 等[154]利用p范数的目标函数控制接触压力分布和变化,同时,为了控制接触压力,他们在耦合牛顿解中采用了基于拉格朗日乘子的接触公式.Ma 等[155]提出了一种解决接触问题的等效静力位移法,该方法通过在静力分析中施加一组位移模拟接触力,所施加位移组的反力等于非线性分析中的接触力.但是,该方法局限于尺寸优化问题.针对多个三维可变形物体互相接触的拓扑优化问题,Fernandez 等[156]使用砂浆逐段接触算法离散接触面,该方法在模拟大变形固-固接触时具有较好的鲁棒性,见图11(i).基于库仑摩擦定律描述摩擦行为,Niu 等[157]发展了一种考虑摩擦接触的弹性结构刚度最大化设计拓扑优化方法.最近,张卫红团队[158]研究了具有最大接触压力约束的弹性接触的拓扑优化设计问题;他们采用了KS 凝聚函数表征一定接触区域的最大接触压力,并将之作为约束引入到拓扑优化列式.
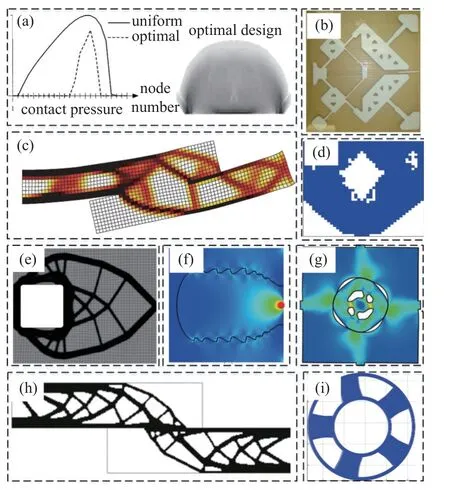
图9 边界非线性连续体拓扑优化: (a) 利用次梯度优化算法设计单边接触条件下板结构[136];(b) 借助正则化接触模型优化设计辅助接触式柔性机构[137];(c) 单侧无摩擦接触结构刚度优化结构[141];(d) 分段常数水平集法解决单侧接触问题[143];(e) 考虑制造约束和单边接触约束的优化设计[146];(f) 考虑滑动接触界面的拓扑优化设计[148];(g) 有限应变下双边接触拓扑优化结果[149];(h) 可提高接触压均匀性的拓扑优化设计[153];(i) 多个三维可变形物体互相接触拓扑优化设计[156]Fig.9 Topology optimization with boundary nonlinearity: (a) utilizing sub-gradient optimization algorithm to design the plate structure under the condition of unilateral contact[136];(b) optimization design of an auxiliary contact flexible mechanism with regularized contact model[137];(c) stiffness optimization of one side frictionless contact structure[141];(d) solving one side contact problem by the piecewise constant level set method[143];(e) optimal design considering manufacturing constraints and unilateral contact constraints[146];(f) topology optimization design considering sliding contact interface[148];(g) topology optimization with bilateral contact under finite strain[149];(h) topology optimization design to improve the uniformity of contact pressure[153];(i) topology optimization design of a multiple 3D deformable object in contact with each other[156]
由此可见,接触带来的强非线性和不连续性对优化建模和求解算法提出了巨大挑战.目前研究已经初步解决了基本的结构优化问题,但是,还存在一定的局限性,比如,主要局限于刚度最大设计问题,需要进一步向其他优化设计目标问题扩展,以适应实际工程需求;通常假设接触区域已知,这与实际工程问题往往有较大出入,亟需进一步的研究.
值得提出的是,近期罗阳军等[159-160]提出了一种基于材料场级数展开的结构非梯度拓扑优化方法,该方法通过模型降阶的思想可为非线性拓扑优化问题(包括材料非线性、几何非线性和接触非线性)提供一个全新的求解思路,已成功解决了类如软体声子晶体、柔性电子和薄膜等非线性结构优化设计,以及动力学优化设计等连续体拓扑优化领域充满挑战性的问题[161-164].此外,引入其他力学约束或者性能需求的非线性拓扑优化问题将变得更加复杂,但也是解决结构实际工程结构优化设计问题必须要考虑的.比如,工程结构设计过程中存在固有的客观不确定性和主观不确定性,进行结构优化设计时需要慎重考虑,邱志平团队近期在考虑不确定性线性结构拓扑优化领域做了大量工作[165-167].另外,文桂林团队[44-49]近年来在稳健性拓扑优化设计方面取得了一些进展,成功将云模型引入到拓扑优化列式,得到了综合主观和客观不确定性的创新性设计;将区间优化问题转化为等效的确定性多工况优化设计问题,大大提升了计算效率,如图10(a)~10(c)所示.而考虑不确定性的非线性拓扑优化设计是一个更具挑战和值得探索的领域.
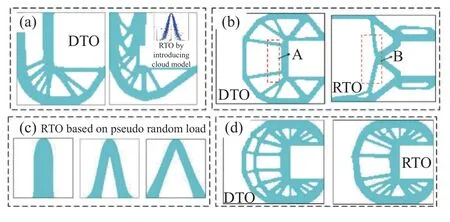
图10 稳健性拓扑优化相关研究: (a) 外载力方向不确定性稳健性优化设计[44];(b) 区间不确定性稳健性优化设计[46];(c) 基于虚拟随机载荷的稳健性拓扑优化设计[48];(d) 外载力位置不确定性稳健性优化设计[49]Fig.10 Research on robust topology optimization: (a) robust topology optimization (RTO) with uncertain direction of external load[46] and compared with that obtained from deterministic topology optimization(DTO);(b) interval uncertainty robust topology optimization[46];(c) robust topology optimization based on pseudo random load[48];(d) robust topology optimization with uncertainty ofexternal load position[49]
4 结论和展望
航空航天、航海工程、机器人等装备领域结构不管从自身材料属性还是使用要求来看,都存在大量的非线性问题,即,材料非线性、几何非线性和边界非线性.而连续体拓扑优化方法为诸如这些结构的设计提供了一种优于传统经验方法的创新手段,因此,研究非线性拓扑优化设计方法具有重要意义.本文详细介绍了国内外在非线性连续体拓扑优化方面的研究进展,可以发现,虽然非线性拓扑优化方法近年来取得了长足的进展,但还尚未成熟,亟需进一步的发展.
(1)材料非线性连续体拓扑优化和几何非线性连续体拓扑优化相对于边界非线性连续体拓扑优化研究较多,原因在于接触问题的强非线性和不连续性对优化模型的建立以及优化算法提出了更高的挑战,特别对于高速碰撞结构和材料的拓扑优化设计问题,需要进一步的研究.材料非线性拓扑优化研究大部分局限于理想弹塑性假设,需要发展适用于更加复杂应力-应变行为的方法,特别是超弹材料结构设计研究.几何非线性拓扑优化大多局限于大变形小应变问题,对于大变形大应变,甚至高应变率问题需要进一步探索;此外,目前方法大多数在拉格朗日法描述框架下进行,非线性拓扑优化循环中有限元响应计算存在精度差的问题,因此,基于欧拉法的几何非线性拓扑优化方法值得进一步的探索.
(2)目前非线性连续体拓扑优化还局限于静力学或准静态系统,而实际工程结构,如卫星、火箭等在发射或者使用过程中,常常表现为复杂的非线性动力学行为[168-169],考虑复杂非线性动力学行为的连续体拓扑优化方法还鲜有人研究,是将来研究的重点方向.此外,非线性连续体拓扑优化由于需要求解大量的非线性方程组,计算效率往往很低,限制了其工程应用,基于多分辨率的思路可以实现高效率和保精度的拓扑优化设计[90,170-173],但该方法仍存在诸如在过滤半径较小的情况容易出现棋盘格现象和QR 模式等问题[174],需要进一步解决.机器学习、并行高性能计算和多重网格法也是克服非线性连续体拓扑优化计算量大的潜在研究方向[6,8,175-178].

