基于量纲分析的弹塑性应力强度因子探讨

张 铮，李泽商，王依兵

(北京航空航天大学航空科学与工程学院, 北京 100191)

0 引言

断裂失效是航天系统结构的主要失效模式，零部件的断裂失效给航天结构的安全运行带来极大威胁。实际航天工程结构(材料)中总是不可避免地存在着各种不同形式的缺陷(如孔洞、裂纹)，孔洞、裂纹、应力集中等问题是引起航天构件失效的主要原因之一，断裂力学是研究裂纹问题的主要固体力学分支学科。自20世纪40年代末产生以来，断裂力学经过半个多世纪的发展，取得了丰硕的研究成果。

断裂力学包含线弹性断裂和弹塑性断裂两大类问题。其中，线弹性断裂力学适用于强度较高的脆性材料的断裂行为，而弹塑性断裂力学适用于裂纹尖端存在较大塑性区的情况。

在线弹性断裂力学中，具有重要的地位和作用的力学参量是表征裂纹尖端场强度的应力强度因子。1957年，Irwin首次提出了应力强度因子的概念，当应力强度因子达到材料断裂韧度时材料发生新的裂纹扩展。弹塑性断裂力学认为裂纹尖端应力场进入塑性，表征线弹性的应力强度因子不再适合表征弹塑性裂纹尖端应力场，而采用J-积分作为弹塑性裂尖场强度的表征量。

张行、洪起超的研究表明，J-积分既适用于表征弹塑性场，又适用于线弹性场；而应力强度因子只适用于线弹性场。然而，相对于应力强度因子简明清晰的物理含义，J-积分的定义式显得相对繁复隐晦，缺乏明确的物理意义。上述问题不仅使得对裂纹尖端场的物理认识存在困难，在应用上也造成材料的弹/塑性断裂判据缺乏一致性。

本文以Ⅲ型裂纹(反平面剪切)问题为例，依据断裂力学已经建立的弹/塑性裂尖场(包括应力强度因子和J-积分)，引入材料弹塑性本构关系，通过理论推导和与现有裂尖场解的对比分析，建立了如线弹性裂尖场应力强度因子形式的弹塑性应力强度因子，用以表征弹塑性裂尖场强度，进而建立可同时适用于材料线弹性和弹塑性断裂的一般性判据。

1 Ⅲ型裂纹问题的弹塑性分析

1.1 基本假设

对于图1所示的典型Ⅲ型裂纹模型，假设截面上任意一点只有垂直截面的位移，即

=(,)

(1)

式中，(,)表示无限长棱柱任意截面内(,)处的位移。

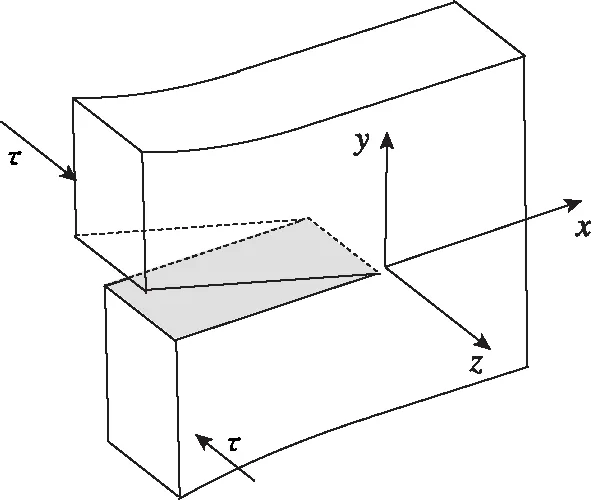
图1 Ⅲ型裂纹的空间和平面图示Fig.1 Spatial representation of model-Ⅲ crack

1.2 平衡方程[16]

平衡方程为

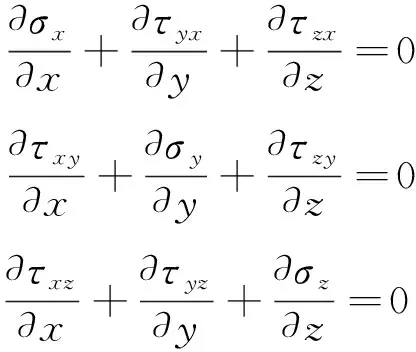
(2)

式中，表示方向的正应力，表示方向平面的方向切应力。

1.3 几何方程

需要说明的是，虽然考虑裂纹尖端场应力进入塑性，但由于裂尖场是大集度场，其区域远小于宏观尺度，材料变形处于小范围塑性状态，因此不失一般性，这里仍然采用线性几何关系，即

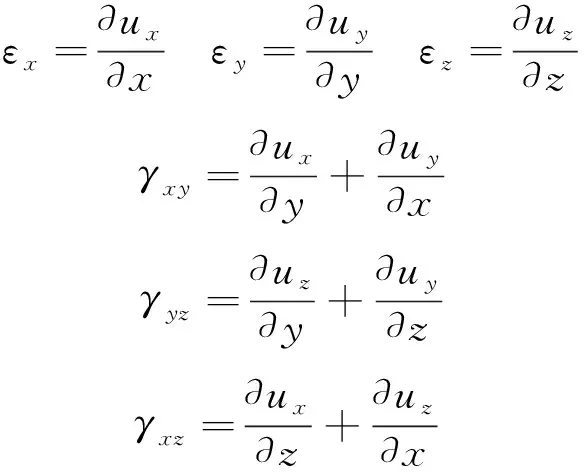
(3)

式中，表示方向正应变，表示切应变。

将式(1)代入上式，有

=====0

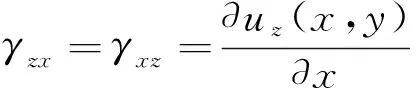
(4)

1.4 本构关系

如式(5)所示，Ramberg-Osgood方程是表示材料弹塑性本构关系的一般性表达式。

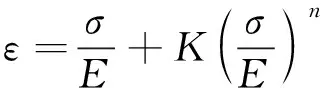
(5)

式中，为杨氏模量，为拉伸应变硬化指数，为硬化系数。

本文所讨论的裂尖场(如“1.3 几何方程”中所述)，虽然是“小范围塑性”场，但在裂尖影响区内，塑性变形是主导性的，即弹性变形远小于塑性变形。因此，可将Ramberg-Osgood方程简化为

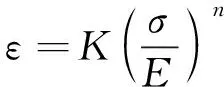
(6)

相似地，有剪切本构方程

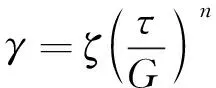
(7)

式中，为剪切硬化系数，为剪切模量。

按照式(6)(7)的形式，Ⅲ型断裂问题的弹塑性本构关系可表达为

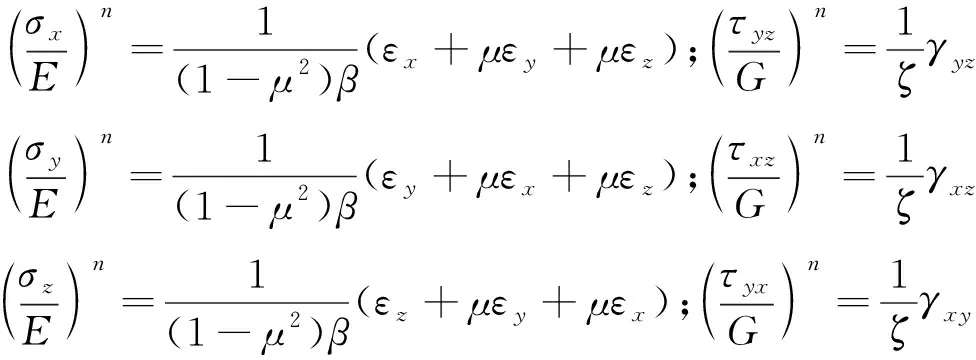
(8)

式中，表示泊松比。

将几何关系式(4)代入弹塑性本构关系式(8)，有

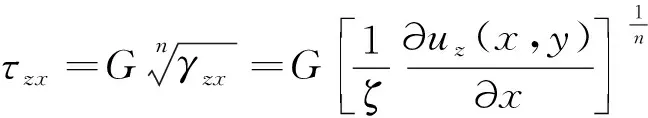
(9)

再将式(9)代入平衡方程式(2)，有

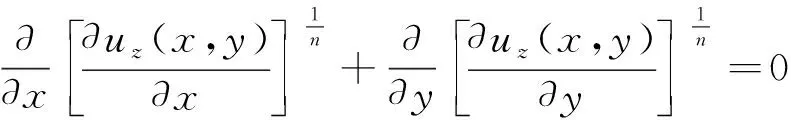
(10)

式(10)结合边界条件即可求得问题解。

2 弹塑性Ⅲ型裂纹问题求解

通过上述推导可知，本问题的控制方程，即式(10)，为二阶非线性椭圆型偏微分方程，断裂力学中常规的复变函数解法难以适用，也缺乏其他简明的求解方法。因此，本文参照现有的断裂力学解，采用半逆解法进一步分析裂尖弹塑性场，从而解析出弹塑性裂尖场的应力场分布。

参看式(1)，并参照线弹性断裂力学分Ⅲ型裂纹分离变量形式的解，假设Ⅲ型裂纹的弹塑性应力场分布函数为

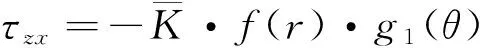
(11)

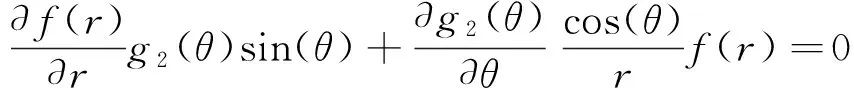
(12)

观察式(12)的形式，参照线弹性场的分布函数，可以发现

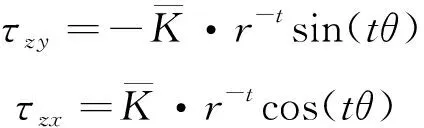
(13)

可以满足该式。进一步，考察应力表示的相容方程

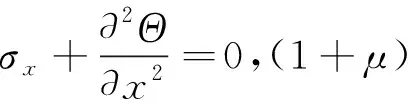
(14)

式中，=++为应力不变量，将应力场函数式(13)代入上述相容方程式(14)，即可证明后者成立。

3 弹塑性应力强度因子的定义

一般断裂力学教科书中，定义线弹性裂尖场的应力强度因子为

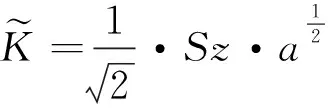
(15)

式中，为载荷对应的远场应力，表示裂纹半长。

对于弹塑性裂尖场而言，通常都是采用J-积分来表征

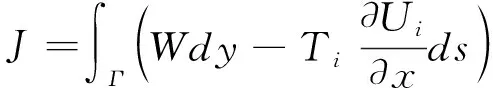
(16)

式中，为从裂纹下表面沿着逆时针方向转到裂纹上表面,包围裂纹尖端的任意积分路径，为外力分量，为位移分量，为积分路径上的线元，为应变能密度。

可见其表达式比较繁复隐晦。相比于线弹性场的特征量即应力强度因子，影响弹塑性裂尖场的因素不是显式的，其作用规律也不是显式的函数形式。

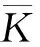
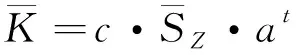
(17)

根据弹塑性断裂力学分析，裂尖应力场可表示为

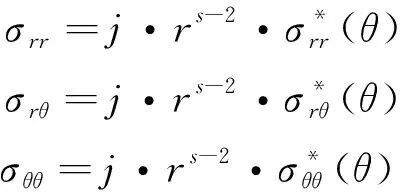
(18)

(19)

综上所述，类比于线弹性裂尖场的应力强度因子，式(17)定义了弹塑性裂尖场的弹塑性应力强度因子，二者的对比如表1所示。

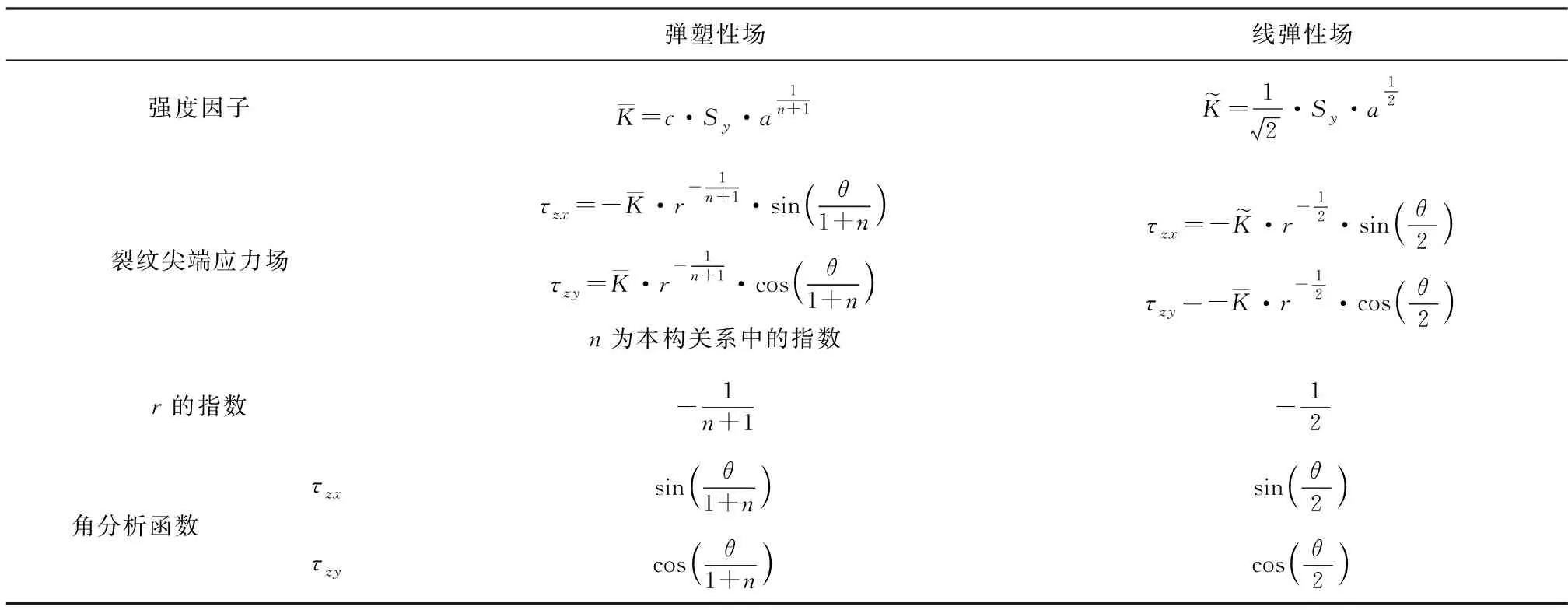
表1 线弹性应力强度因子与弹塑性应力强度因子

4 弹塑性应力强度因子的合理性

首先，对于线弹性裂尖场，应力强度因子是表征应力场强弱的力学参量。当载荷造成裂纹扩展时，应力强度因子的临界值可视作材料的断裂强度，即材料断裂韧度。

其次，本文依托弹塑性裂尖场定义了相应的弹塑性应力强度因子，该参量同样表征裂尖应力场的烈度/集度；当载荷造成裂纹扩展时，弹塑性应力强度因子可以替代J-积分，其临界值同样可以视作材料断裂韧度，也就是说，可以根据本文定义的弹塑性应力强度因子建立材料断裂的新判据，而弹塑性应力强度因子的含义远比J-积分要简明。这是本文研究的重点。

由此，建立与弹塑性应力强度因子相应的实验方法和相应断裂韧度的测量方法，不仅具有简明的理论基础，也将有助于简化实验，方便应用。这也是本文研究的意义。

需要指出的是，本文方式同样适用于定义Ⅰ型和Ⅱ型裂纹的弹塑性应力强度因子，表征其弹塑性裂尖场的集度。

5 结论

综上所述，本文首先基于断裂力学基本概念和理论，对基于Ⅲ型裂纹(反平面剪切问题)进行分析，在弹塑性场中建立了该问题的几何方程、本构方程和平衡方程。

然后参照线弹性场中裂纹尖端应力分布函数，建立了弹塑性场中的裂纹尖端应力分布函数，并基于理论推导，在裂纹尖端应力分布函数、强度因子、的指数和角分布函数4方面对比弹塑性场与线弹性场，定义了类比于线弹性场中应力强度因子的参数，即弹塑性应力强度因子，来表征弹塑性裂纹尖端应力场强度。

本文对提出的弹塑性应力强度因子在表达形式、物理意义、量纲和普适性等方面分别进行分析，阐述了弹塑性应力强度因子涵盖弹塑性裂纹尖端场的表征意义，明确了其概念的内涵、定义和合理性基础，因而确立了该参量对弹塑性裂纹尖端场固有特质的表征。由此也说明，根据弹塑性应力强度因子可以建立适用于材料弹性/弹塑性断裂的一般性判据。