倾斜圆柱结构涡激振动研究进展1)

徐万海 马烨璇

(天津大学水利工程仿真与安全国家重点实验室,天津 300072)

引言

圆柱结构物置于一定速度的流场时,流体边界层会沿结构壁面分离,易使附近的流体破碎形成旋涡.圆柱后缘的旋涡周期性交替泻放,改变了结构表面的压强分布,产生了作用于结构上的流体力.若结构可变形或端部未固定,旋涡泻放产生的流体力可诱发结构振动,结构的振动又反过来影响旋涡脱落模式,这种典型的流-固耦合现象被称之为“涡激振动(vortex-induced vibration,VIV)”.涡激振动在工程中十分普遍,例如海洋工程中的立管、海底悬跨管线、系泊缆、平台张力腿、水下悬浮隧道等,土木工程中的高耸建筑、桥梁斜拉索等,核工程中的热交换器等,这些圆柱结构极易发生涡激振动.VIV 的主要危害是诱使结构出现疲劳损伤,降低结构使用寿命.学术界和工程界广泛关注了圆柱结构的涡激振动机理及抑制方法,目的是减轻涡激振动对结构的危害,并取得了大量代表性成果[1-11].

人们对涡激振动的认识是一个逐步深入的过程,从“固定刚性圆柱绕流”到“弹性支撑刚性圆柱VIV”,再到“柔性圆柱VIV”.通过固定刚性圆柱绕流研究,明晰了不同雷诺数(Re=UD/ν,其中U为来流速度,D为圆柱外径,ν为流体的运动黏度)条件下光滑圆柱的尾流形态,并确定得到了平均阻力系数、升力系数、斯托罗哈数(St=fsD/U,其中fs为旋涡脱落频率)随Re的变化关系式[12-14].通过弹性支撑刚性圆柱VIV 研究,揭示了“锁定(lock-in)”现象和VIV 相关机理.“锁定”范围、振幅变化规律、尾涡模式、流体力系数等是刚性圆柱VIV 中的典型规律特征.雷诺数Re、质量比(m*=4ms/(ρπD2),其中ms为圆柱结构单位长度的质量,ρ为流体密度)、阻尼比ζ、自由度数目等也是刚性圆柱VIV 中的重要影响参数.

雷诺数Re对VIV 中所关注的多数问题均会产生影响,在亚临界范围(Re=3 × 102～ 3 × 105)内,圆柱VIV 具有相近的规律[15-20].质量比主要影响“锁定”范围和振幅变化[21-24],随着质量比减小,流-固耦合作用更为强烈,结构可在更宽的流速范围内产生大幅振动.VIV 最大响应幅值可通过由质量比和阻尼比乘积组成的参数来描述,假定最大响应幅值是质量-阻尼参数的单调函数,根据实验数据可预测VIV 最大响应幅值[17,25-26].圆柱在垂直来流方向—横流向(cross-flow,CF)和平行来流方向—顺流向(in-line,IL)均能发生振动.顺流向振动对横流向振动的影响主要取决于质量比的大小,当质量比小于6.0 时,顺流向振动对横流向振动影响显著[27-28].VIV 的流体力系数与结构响应振幅和频率密切相关,由于圆柱VIV 的自激励-自限制特性,流体力系数与振幅之间具有典型的非线性关系[29-30].通过刚性圆柱受迫振动实验中获取的流体力系数云图常用于VIV 预报[31-32].

对于长径比(圆柱长度L与直径D的比值)较大的柔性圆柱,其发生涡激振动时结构常出现弯曲变形,在轴向不同位置处响应位移和涡流场差别很大[33].柔性圆柱结构的VIV 通常激发高阶模态,伴随有多模态振动、宽带随机振动、涡致行波等重要特征[34-36],振动特性更为复杂.随着流速增大,柔性圆柱涡激振动的各阶模态逐步被激发,低阶模态振动向高阶模态振动转变的过程中,存在激烈的模态竞争,会导致振动位移出现急剧降低[35].柔性圆柱发生涡激振动时,结构轴向存在能量输入区和能量耗散区,振动能量以行波的方式由能量输入区传播至能量耗散区[37-38].柔性圆柱VIV 的流体力系数与刚性圆柱相比存在一定差异[39-42],除了响应频率和响应位移,圆柱横流向和顺流向的相位差也会对升力系数和脉动阻力系数产生显著影响[42].

上述关于圆柱结构涡激振动的研究中均假定来流方向垂直于结构轴向.经过数十年的研究,人们已对垂直来流作用下圆柱结构VIV 的相关机理有了较为全面的理解和认知.如图1 所示,实际工程中,来流方向并不总是与圆柱结构的轴向垂直.当圆柱结构倾斜放置于流场中时,结构后的尾流形态与圆柱垂直放置时存在显著差异,流-固耦合作用机理更为复杂多变.早期,为了简化倾斜圆柱绕流问题,提出了不相关原则(independence principle,IP)[43-44].不相关原则认为: 可将来流速度分解为垂直圆柱结构轴向和平行圆柱结构轴向的两个速度分量,仅考虑垂直圆柱轴向速度分量的影响,平行圆柱轴向速度分量的影响可忽略不计.多年来,学术界持续围绕“固定倾斜刚性圆柱绕流、弹性支撑倾斜刚性圆柱VIV、倾斜柔性圆柱VIV”中不相关原则的适用性问题开展研究,对倾斜圆柱结构VIV 机理的认识逐渐清晰.本文将对国内外在倾斜圆柱结构涡激振动的现象观察、机理认识和响应分析等方面的研究进展进行全方位综述,重点对倾斜圆柱结构涡激振动的响应和流体力特性进行总结阐述,探讨不相关原则的适用范围,并对未来的研究工作进行展望.

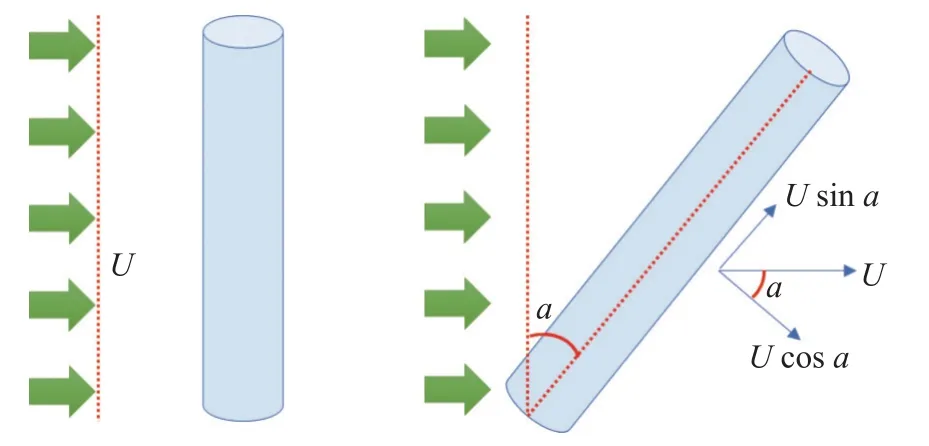
图1 垂直圆柱与倾斜圆柱结构示意图Fig.1 Schematic diagram of vertical and inclined cylinders

1 固定倾斜刚性圆柱绕流

1.1 斯托罗哈数

斯托罗哈数St可用于表示旋涡脱落频率,因此St成为倾斜圆柱绕流中被重点关注的参数之一.早期一些学者通过风洞实验,研究了Ren=50～150 (Ren=UcosaD/ν)范围内St与圆柱倾斜角度a之间的关系[45-46].Ren=50～150 时,垂直圆柱的St随Re逐渐增大,因此拟合倾角与St的变化曲线时,需同时考虑St与Re经验关系Stn*(0)=0.212 -4.5/Ren[47].为了便于分析IP 原则的适用性,定义了等效斯托罗哈数Stn=fsD/(Ucosa).通过比较Stn与Stn*(0)的比值Stn/Stn*(0) 刻画倾角对St的影响.当a=0°～35°时,Stn/Stn*(0)接近1.0,表明在上述倾角范围内St的结果适用于IP 原则.当a超过35°后,Stn/Stn*(0)的值呈指数增长,a=70°时,Stn/Stn*(0)增大至2.0 左右.虽然在此倾角下,St不适用于IP 原则,但仍可以通过拟合得到倾角a与St之间的经验关系.

随后,学者们进一步通过风洞实验,研究了Ren=160～1100 范围内St与圆柱倾斜角度a之间的关系[48].当a=0°～30°时,斯托罗哈数的结果适用于IP 原则.当a超过30°后,随着倾角增大St的变化曲线仍然保持连续,可以拟合得到经验关系式.但St随倾角的变化曲线与Ren=50～150 条件下的变化曲线并不吻合.不同倾斜圆柱绕流实验研究中St结果存在一定差异,如图2 所示,主要对比倾斜圆柱斯托罗哈数Stn与垂直圆柱斯托罗哈数St0比值的结果.Surry 等[49]发现在Re=4000～63 000 范围内,直到a=40°～50°时,St结果仍能适用于IP 原则.Thankur 等[50]在Ren=296～513 条件下观测到的倾角a=0°,30°,60°时St结果与Van Atta[46]在Ren=50～150 条件下的结果较为接近,表明IP 原则的适用范围为倾角小于30°.Zhou 等[51]综合对比了不同倾斜圆柱绕流的实验结果,在设定许可偏差为8%的前提下,认为倾角不超过40°时IP 原则适用,当倾角为60°,采用不相关原则预估的St与实际值相差40%.

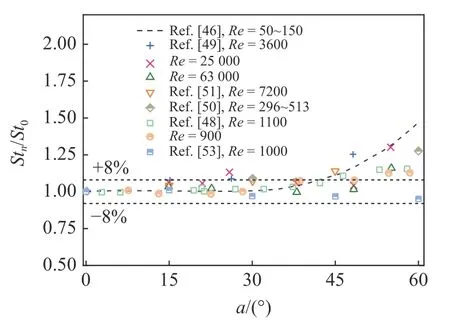
图2 St随倾角a的变化Fig.2 Stversus the inclination angle

不同的倾斜圆柱绕流数值模拟研究中得到St结果也并不完全一致.Willden 等[52]采用DNS 方法模拟了倾斜圆柱结构的绕流过程,发现倾角不超过40°时St的结果适用IP 原则.Zhao 等[53]通过设置周期性边界条件模拟了无限长圆柱结构的绕流问题,发现当倾角为60°时,仍能采用IP 原则预估St.Thapa 等[54]开展了近壁倾斜圆柱绕流数值模拟,发现倾角不超过30°时St的结果适用IP 原则.Liang等[55]开展了有限长倾斜圆柱绕流的数值模拟研究,发现了不同轴向位置处的St存在显著差异,倾角为30°时,圆柱下游区域的St适用于IP 原则,圆柱中部和上游区域的St不适用于IP 原则.高洋洋等[56]基于OpenFOAM 开展了不同雷诺数下倾斜圆柱绕流数值模拟.Re=100 和1500 条件下,St的结果在倾角60°时仍适用于IP 原则;Re=3900 时,St的结果仅在倾角不超过15°时适用于IP 原则.

不同研究之间St结果产生差异的原因主要有两个方面: (1)雷诺数范围不同;(2)不同实验研究中圆柱端部的边界条件差异较大.虽然Ramberg[48]通过分析广义斯托罗哈数(考虑尾流宽度和基准压力)随广义雷诺数(考虑尾流宽度和基准压力)的变化情况,将倾角对斯托罗哈数的影响规律进一步推广到更高的雷诺数范围[57-58],但雷诺数仍会对适用IP 原则的临界倾角产生一定影响.Surry 等[49]发现Re=25 000 和63 000 时,临界倾角为50°,而Re=3900 时,临界倾角为40°.高洋洋等[56]发现Re=3900 时的临界倾角仅为15°,远小于Re=100 和1500 时的结果.由此可见,雷诺数会对临界倾角产生影响,但也并非是唯一影响因素.

圆柱端部边界条件的差异也是导致不同倾斜圆柱绕流研究中斯托罗哈数结果存在偏差的重要原因.圆柱结构绕流过程中,流体在结构端部存在三维效应,使圆柱结构相当跨度上的流场也具有三维流动特征[59-60].圆柱端部边界条件的变化,易引起尾流场特性发生变化,进一步导致斯托罗哈数改变.Ramberg[48]观测了倾斜圆柱四种端部边界条件下(平面边界、半球型边界、锥型边界、端板边界)的尾流形态.其中半球型边界和锥型边界下圆柱的尾流形态较为接近.在平面边界时,倾斜圆柱后的尾涡脱落角度总是小于倾斜角度,倾角越大,尾涡脱落角度的偏差也越大.当尾流脱落角度与倾角接近,即尾涡形成的轴向涡流与结构轴向平行时,St结果将适用于IP 原则.尾涡的脱落角度对边界条件变化十分敏感,导致不同研究之间临界倾角存在一定差异.通过调整圆柱端部边界,使轴向涡流平行于圆柱轴向便能使St在较大倾角时也适用于IP 原则.Zhao 等[53]在数值模拟中采用周期性边界条件,规避了端部边界的影响,倾角为60°时,St结果仍适用于IP 原则,这也进一步证实了端部边界的重要影响.

1.2 尾流场特性

倾斜圆柱绕流的尾流形态与垂直圆柱绕流存在明显不同.Ramberg[48]实验观测了Ren=160～1100 范围内倾斜圆柱绕流的尾流形态,如图3 所示.圆柱垂直放置或倾角极小时,圆柱某一截面的流向涡泻放后,通常与相邻截面的旋涡连成一条弯曲的轴向涡线(vortex line),轴向涡线并不稳定,在向下游发展的过程中极易破散.随着倾角的增大,轴向涡线的稳定性增强,且更加平直,轴向涡线的偏斜角度略大于圆柱的倾角.对于倾角更大的情形,圆柱上游端的轴向涡线沿流向产生关联,形成网状涡环(loop).倾角进一步增大,网状涡环在轴向发生脱离,形成一条波浪线型的流向拖尾(trailing).因此,可将倾斜圆柱后的尾流概况分为三种模式: 形成轴向涡线的涡脱落模式(vortex-shedding regime)、形成波浪线型的拖尾模式(trailing regime)以及两者之间的过渡模式(transition).

图3 文献[48]观测到的倾斜圆柱尾流模式Fig.3 Wake patterns of flow around an inclined cylinder in Ref.[48]

倾斜圆柱的上述三种尾流模式主要受倾角、雷诺数和端部边界条件的影响,如图4 所示.在Ren=160～1100、倾角a=0°～60°范围内,拖尾模式发生在低雷诺数区域,且倾角至少要高于40°.半球形边界(hemispherical)和锥型边界(coned)条件下,三种尾流模式的分布区域较为一致,涡脱落模式占据着大部分区域.在平面边界(flat)条件下,拖尾模式所占区域进一步缩减,Ren超过500 后,倾角0°～60°范围内尾流模式均为涡脱落模式.

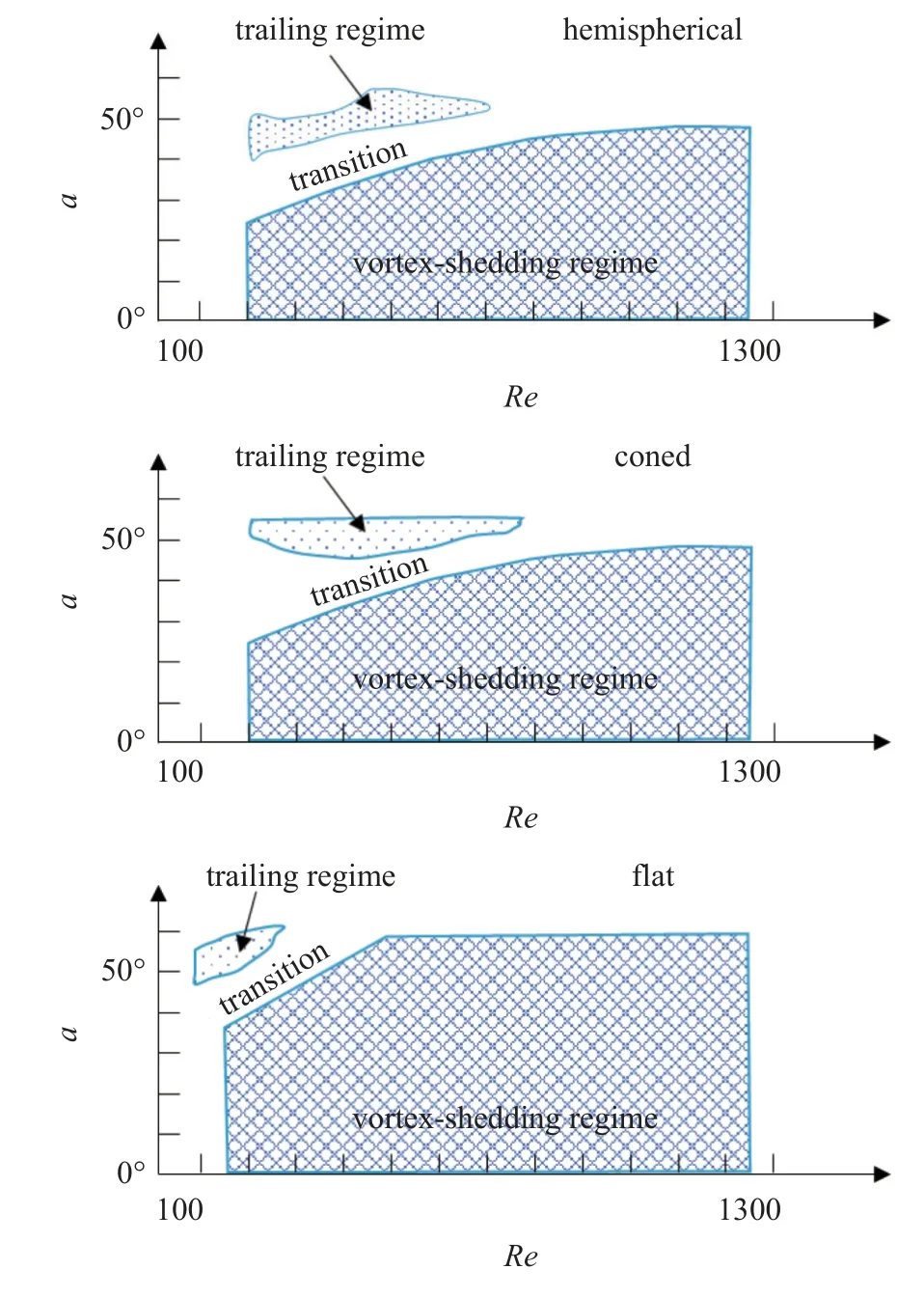
图4 倾斜圆柱尾流模式区域[48]Fig.4 Wake pattern regions of flow around an inclined cylinder[48]

随着数值模拟和流场观测技术水平的提升,倾斜圆柱绕流过程中的尾流场特性得到了更为全面的呈现[50,56,61-68].Thankur 等[50]在Ren=296～513 条件下观测了倾角a=0°,30°,60°时圆柱绕流的尾流特征.a=0°时,不同截面尾涡汇合形成的轴向涡线与圆柱轴向平行,但涡线表现出微弱的波动;a=30°时,圆柱上游端尾流区涡线的偏斜角度略小于倾角,其他尾流区的涡线与圆柱轴向平行;a=60°时,尾流区的涡线沿轴向发生弯曲,上游端尾流区涡线偏斜角度显著小于倾角.Wang 等[68]数值分析了Re=14 000 条件下倾斜圆柱绕流的尾流特性,如图5 所示.a=0°时,圆柱后缘脱落的卡门涡被定义为“主涡”,不同截面的主涡形成了波浪型涡线;a=30°时,不同截面的主涡形成的涡线较为平直;a=45°时,主涡A1 被“二次涡”A2 打乱;a=60°时,尾流中主涡消失,取而代之的是稳定的拖尾,这与Ramberg[48]的实验观测结果近乎一致.倾角超过30°后,圆柱后的旋涡脱落受到了显著的抑制.高洋洋等[56]进一步研究了Re对倾斜圆柱尾流特性的影响.Re=100 条件下,倾角不超过45°时,尾流涡线与圆柱轴向近乎平行,涡线沿轴向并无显著变形,表现为显著的二维特性,倾角为60°时,旋涡脱落被完全抑制;Re=1500 条件下,倾角0°时,由于旋涡脱落沿轴向存在相位差异,轴向涡线略微弯曲,倾角为30°时,尾流形态发生显著变化,轴向产生较强的轴向流,倾角超过45°后,旋涡脱落受到严重抑制,细碎旋涡逐渐消失,尾流宽度减小;Re=3900 条件下的结果与Re=1500 时的结果整体相近,流场沿圆柱轴向的掺混更加强烈,三维特性更为明显.

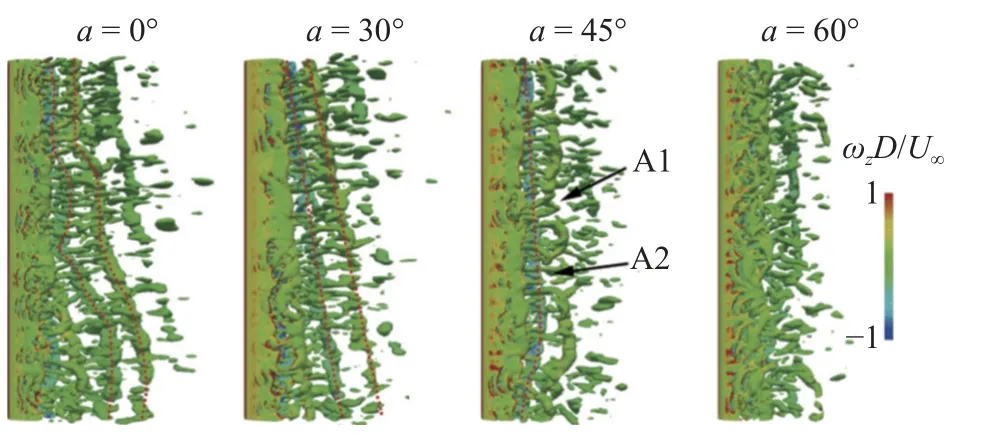
图5 文献[68]数值模拟的倾斜圆柱尾流模式Fig.5 Wake patterns of flow around an inclined cylinder in Ref.[68]

导致倾斜圆柱与垂直圆柱绕流现象产生差异的主要原因是轴向二次流.Kawamura 等[69]数值模拟了Re=2000、倾角a=30°圆柱的绕流过程,发现在靠近圆柱背流侧区域沿圆柱轴向形成了二次流,流动方向由圆柱上游端至圆柱下游端.改变圆柱的边界条件会对轴向流产生影响,倾斜圆柱安装端板后,轴向流沿圆柱轴向发生变化,导致靠近上游端板区域的尾涡较小、尾迹较窄,而靠近下游端板区域的尾涡较大、尾迹较宽.Shirakashi 等[70]实验观测到了倾斜圆柱背流侧产生强烈的轴向二次流,使旋涡脱落不规则、频率降低,采用平板截断轴向二次流后,板间区域内旋涡脱落规律、频率回归正常水平.轴向流诱使倾斜圆柱尾涡脱落不稳定的机制较为复杂.Wang 等[68]认为在大倾角情形下,强度较大的轴向流起到了分离板的作用,抑制了旋涡的生成.Marshall[71]认为大倾角时旋涡脱落不稳定有两方面原因,一方面是圆柱尾流旋涡的开尔文-亥姆霍兹不稳定,虽然尾涡的延展和剪切作用能一定程度上抑制开尔文-亥姆霍兹不稳定[72-73],但在大倾角情形下尾流中会形成缠绕在卡门涡周围并与之相互作用的涡流;另一方面,尾流场中的轴向速度与旋涡中心的轴向速度差过大时易破坏旋涡的稳定性[74-75],在大倾角情形下尾流场中的轴向速度较大更加不利于旋涡的稳定.Zhou 等[51]通过数值模拟得到了倾斜圆柱绕流中自由流场的轴向速度和旋涡中心的轴向速度,随着倾角增大,轴向速度差增大,进而抑制尾流旋涡.

1.3 流体力系数

由于轴向流的影响,倾斜圆柱绕流的流体力特性与垂直圆柱绕流存在很大不同.倾斜圆柱绕流过程中的流体力变化对边界条件十分敏感,靠近圆柱端部区域的流体力系数通常会沿结构轴向发生剧烈变化[76-79].轴向流会减弱尾涡的强度,使圆柱表面的脉动压力系数减小、平均阻力系数降低[56,77,80],升力系数随倾角并非呈单调变化[53,56,81-83].

为了验证IP 原则是否适用,通常根据倾斜状态下流体力系数与垂直状态下流体力系数的比值,与cos2a进行对比.高洋洋等[56]研究了倾角对有限长圆柱绕流流体力系数的影响.对于平均阻力系数,倾角不超过30°时,IP 原则适用;倾角达到45°时,平均阻力系数的偏差约为22%～37.16%;倾角达到60°时,平均阻力系数的偏差约为46%～93.96%.对于升力系数均方根,Re=100 条件下,倾角不超过45°时,IP 原则适用;Re=1500 和3900 条件下,所有倾角时的偏差均大于20%,IP 原则不适用.

为了规避边界条件的影响,一些学者研究了倾角对无限长圆柱流体力系数的影响规律[53,68,82-83],如图6 所示.对于平均阻力系数,倾角不超过30°时,平均阻力系数不随倾角发生显著改变;倾角达到45°后,平均系数高于IP 原则的预测值,特别是当倾角达到60°后[53,82-83].对于升力系数均方根,倾角不超过30°时,升力系数均方根随倾角逐渐减小,在30°时达极小值;倾角超过30°后,升力系数均方根逐渐增大[53,83].阻力系数均方根随倾角的变化更为复杂,倾角不超过30°时,阻力系数均方根先减小后增大;倾角超过30°后,阻力系数均方根先减小而后变化较为缓和[53].

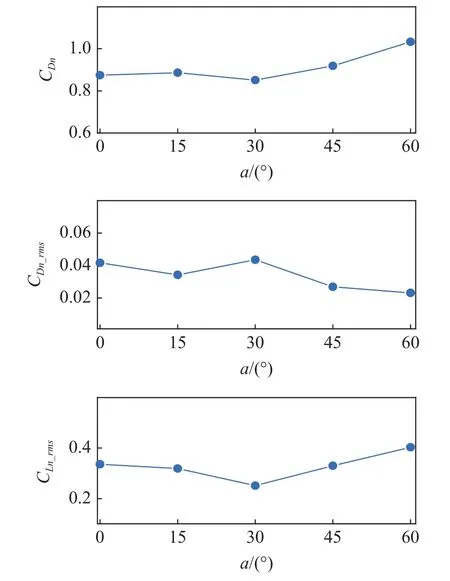
图6 倾斜固定圆柱绕流的流体力系数[53]Fig.6 Fluid force coefficients of an inclined stationary cylinder[53]

1.4 倾斜刚性固定圆柱IP 原则适用范围

倾斜圆柱绕流过程中,对于St、流体力系数等不同结果,IP 原则的适用范围并不相同.此外,IP 原则的适用范围也受雷诺数和圆柱边界条件影响.

对于St,决定其是否满足IP 原则的主要因素是倾斜圆柱后的轴向涡线是否与圆柱轴向平行[48].受圆柱边界效应的影响,有限长圆柱绕流的St通常在倾角不超过30°～40°时适用于IP 原则[45-51].消除边界效应的影响后,无限长圆柱绕流的St在倾角达60°时仍能适用于IP 原则[53,66].对于平均阻力系数,通常在倾角不超过30°时,IP 原则适用;倾角超过30°后,平均阻力系数高于IP 原则的预报结果[53,66,83].对于升力系数均方根,在不规避边界效应影响时,有限长倾斜圆柱的升力系数均方根在所有倾角下都不适用于IP 原则[56];消除边界效应的影响后,无限长圆柱的升力系数均方根在倾角不超过15°时适用于IP 原则[53,83].由于倾斜圆柱绕流的研究中对阻力系数均方根的关注较少,尚难以确定IP 原则的适用范围.

2 弹性支撑倾斜刚性圆柱VIV

2.1 振动响应

倾斜圆柱绕流的尾流特征已经极其复杂,而圆柱振动又能反过来影响尾迹流场,导致弹性支撑倾斜圆柱的涡激振动成为更为复杂的流-固耦合问题.响应频率与振动幅值是倾斜圆柱VIV 研究中关注的重要信息.Nakagawa 等[84]在风洞中观测了大质量比(m*=O(103))倾斜刚性圆柱VIV 响应,圆柱的振动幅值较低,无量纲横流向位移y/D不超过0.15(其中y为横流向振动位移).振动位移与阻尼之间的关系并未受到倾角的显著影响,但涡激振动的“锁定”区域随倾角发生明显变化.倾角为45°时,“锁定”区域显著变窄.小质量比倾斜刚性圆柱VIV 表现出与大质量比条件下不同的响应特性.

对于仅允许横流向振动的小质量比刚性圆柱,倾角对其振动响应的影响较小.Franzini 等[85]实验观测了倾斜刚性圆柱横流向VIV,质量比为2.5,雷诺数范围为2000～8000.倾角为20°和45°时,振动位移相较于垂直圆柱降低了约15%,达到最大位移时对应的等效约化速度基本一致.倾斜圆柱和垂直圆柱“锁定”区域的范围接近,“锁定”时振动响应频率略高于结构固有频率.一些学者[86-87]通过数值模拟研究得到了与实验研究[85]较为一致的结论.Zhao[86]采用周期性边界条件,规避了圆柱端部边界的影响,重点关注了倾角45°条件下的振动响应,在Re=150 和1000 条件下,倾斜圆柱的振动位移和响应频率与垂直圆柱的结果高度吻合.Wu 等[87]数值研究了Re=20 000 条件下的倾斜圆柱VIV 响应,通过分析振动位移、响应频率和“锁定”区间,表明倾角为45°时IP 原则仍然适用.

随后,部分学者进一步扩大了倾角范围,关注了倾角在45°～75°条件下倾斜刚性圆柱的横流向VIV(雷诺数范围为500～4000)[88-89].倾角对响应频率的影响较小,但对振动位移和“锁定”范围影响较大.倾角不超过45°时,最大振动位移不随倾角发生显著变化,与文献[86-87]的结果一致;倾角为55°、65°和75°时,最大振动位移的下降幅度分别为8%、11%和40%.“锁定”区域随倾角的变化较为复杂.倾角不超过20°时,“锁频”区域对应等效约化速度4～11;倾角为45°和55°时,“锁频”区域对应等效约化速度4～9;倾角为65°时,“锁频”区域对应等效约化速度4～6;倾角为75°时,“锁频”区域对应等效约化速度3～5.随着倾角增大,“锁频”范围逐渐变窄,当倾角增大至65°后,“锁频”区域内振动位移的曲线形式与小倾角时相比变化显著.

对于弹性支撑倾斜刚性圆柱VIV,顺流向振动与横流振动存在显著耦合作用[90].Franzini 等[90]开展了弹性支撑倾斜刚性圆柱的两自由度涡激振动实验研究,雷诺数范围为3000～15 000.两自由度振动的响应特性与单自由度的响应特性差异明显,如图7所示.对于横流向振动位移,倾角不超过20°时,最大振动位移基本不随倾角发生显著变化;倾角为30°和45°时,最大振动位移分别降低了约14% 和28%,最大位移对应的等效约化速度降低.对于顺流向振动位移,倾角不超过10°时,最大位移及最大位移对应的等效约化速度不发生变化;倾角为20°时,最大位移对应的等效约化速度后移;倾角为30°和45°时,最大位移显著下降,最大位移对应的约化速度偏差较大.对于振动响应频率,倾角超过30°后,横流向响应频率在“锁定”区显著高于其他倾角工况下的结果,在多数流速工况下,顺流向的响应频率与横流向接近;倾角不超过20°时,顺流向的响应频率大致为横流向2 倍.由于顺流向和横流向响应频率之间的关系发生变化,倾角超过30°后,圆柱的运动轨迹不再为典型的“8”字型或新月型.

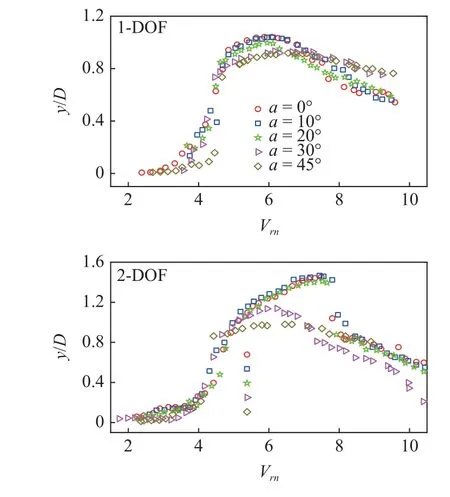
图7 倾斜刚性圆柱VIV 的横流向位移[90]Fig.7 Cross-flow displacements of an inclined rigid cylinder undergoing VIV[90]

倾斜圆柱VIV 响应对边界条件变化较为敏感,Jain[89]和Franzini 等[90]在实验中研究了圆柱端部边界的影响.他们开展的实验中,圆柱的一端为自由水面,一端为水槽底边壁.通过正负倾角来表示两种不同的边界条件,正倾角时,倾斜圆柱上游端为自由水面,下游端为水槽底边壁;负倾角时,上、下游端的边界条件相反.在Franzini 等[90]的实验中,正倾角条件下,“锁定”区域的范围相比负倾角条件下显著变窄;倾角超过20°后,最大位移的降低幅度在正、负倾角条件下差异显著.正、负倾角时,圆柱两端的边界条件不对称导致了上述差异的产生.对于倾斜圆柱,尾流场中通常产生由圆柱上游端向下游端的轴向流,正、负倾角时轴向流的方向发生变化.由自由水面流至池底边壁的轴向流和反方向的轴向流对圆柱的VIV 产生了不同的影响.

2.2 尾流场特性

倾斜圆柱的振动会改变尾流场,Ramberg[48]通过圆柱受迫振动实验,推测了倾斜圆柱自激振动的“锁定”区间,随着倾角由0°增大至50°,“锁定”范围逐渐变窄,但自激振动的最大位移并不一定显著降低,这一推论与后续的倾斜圆柱自激振动研究结果基本一致[85,88,90].通过进一步观测流场发现,倾斜圆柱振动过程中迫使尾流中轴向涡线的偏斜角度与圆柱倾斜角度十分接近.因此,Ramberg[48]认为倾斜圆柱自激振动时,在倾角高达50°时IP 原则仍然适用.

随后,一些学者通过实验和数值方法对倾斜刚性圆柱VIV 的尾流场进行了更加深入的研究[82,86-92].Jain[89]实验观测了倾斜刚性圆柱VIV 过程中的尾流形态,倾角为0°,45°和65°条件下,“锁定”刚刚发生之时,倾斜圆柱后形成的轴向涡线与圆柱轴向平行,这一结果与Ramberg[48]的观测结果一致.Zhao[86]采用数值方法对比了倾角为0°和45°时圆柱尾流场中的涡结构.尾流主要由垂直圆柱轴向的旋涡主导,紧靠在圆柱背侧的轴向涡线与圆柱轴向平行,但倾角为45°时不同位置的旋涡存在相位差,旋涡在空间上错落分布.Lucor 等[82]数值研究了倾角60°,70°时圆柱VIV 的尾流特征.虽然圆柱尾流中形成的轴向涡线整体与圆柱轴向平行,但局部位置会发生螺旋扭曲.强度较高的卡门涡缠绕在轴向涡周围,形成类似于倾斜固定圆柱绕流中的二次涡结构[68],使卡门涡与圆柱轴向不再垂直,而是沿着螺旋路径发展.部分卡门涡沿流动方向倾斜,另一部分沿流动的法向倾斜.大倾角情形下的这种尾流形态,使作用在圆柱上的流体力与垂直状态时发生显著变化,最终导致振动响应特性的差别.

圆柱的边界条件对尾流场具有重要影响.Franzini 等[90]实验观测了倾斜圆柱某一截面的尾流模式,实验中自由液面和底边壁会对尾流形态产生影响,倾角为45°时,流场中的轴向流起到了分离板的作用,阻碍了圆柱两侧剪切层的相互作用.Wu 等[87]在数值模拟中通过设置周期性边界条件规避了圆柱端部边界的影响,倾角45°条件下,圆柱振动的初始分支区域,尾涡呈2S 模式,圆柱振动的上分支区域尾涡呈2P 模式,与垂直圆柱的尾流类似.

2.3 流体力系数

对于大质量比(m*=O(1 03)) 圆柱结构,Nakagawa 等[84]认为倾角对升力系数的影响较小.由于在Nakagawa 等[84]开展的风洞实验中,不同倾角条件下结构阻尼比并不完全相同,所以并未对不同倾角时圆柱的升力系数进行直接对比,而是分析了倾角为0°,15°,30°和45°时升力系数随振动位移的变化关系.结果表明,倾角不超过45°时,升力系数、随振动位移的变化具有一致的规律,IP 原则适用.

小质量比倾斜圆柱VIV 的流体力系数受多种因素制约.Franzini 等[85,90]实验观测了倾斜圆柱仅发生横流向振动时的流体力系数.研究发现: 流体力系数主要受到倾角和边界条件的影响.正、负倾角(正倾角时圆柱上游端为自由水面,下游端为水槽底边壁,负倾角时相反)两种不同边界条件下,倾角对升力系数最大值影响不大,但对升力系数变化曲线的形式产生一定影响,升力系数开始增大或减小时对应的等效约化速度存在差异.不同边界条件下,相同角度时,升力与横流向位移之间的相位差也存在显著差异.对于平均阻力系数,正倾角条件下,平均阻力系数最大值随角度增大而减小,倾角45°时,降低了约33%;负倾角条件下,倾角不超过30°时,平均阻力系数最大值随倾角略有下降,倾角45°时,最大值降幅约33%.Lucor 等[82]数值研究了倾角60°,70°时圆柱VIV 的流体力系数.在相近雷诺数条件下,“锁定”发生时,倾斜圆柱的平均阻力系数、脉动阻力系数均方根、升力系数均方根均高于IP 原则的预估值.

Franzini 等[90]实验研究了倾斜圆柱发生双自由度振动时的流体力特性,如图8 所示.对于平均阻力系数,正倾角条件下,倾角为10°,20°时,平均阻力系数略有升高,但最大值基本相当,倾角为30°时,平均阻力系数最大值有所下降,倾角为45°时,平均阻力系数显著降低且最大值对应的等效约化速度减小;负倾角条件下,倾角10°时,平均阻力系数升高,倾角为20°时,平均阻力系数变化不明显,倾角为30°和45°时,平均阻力系数最大值分别降低约14%和29%,最大值对应的等效约化速度显著减小.升力系数均方根随倾角的变化规律较为复杂.倾角为10°时,升力系数均方根最大值略有降低;倾角为20°时,最大值明显升高;倾角为30°和45°时,最大值随倾角增大而降低,正倾角条件下分别降低约56%和78%,负倾角条件下分别降低约35%和74%.

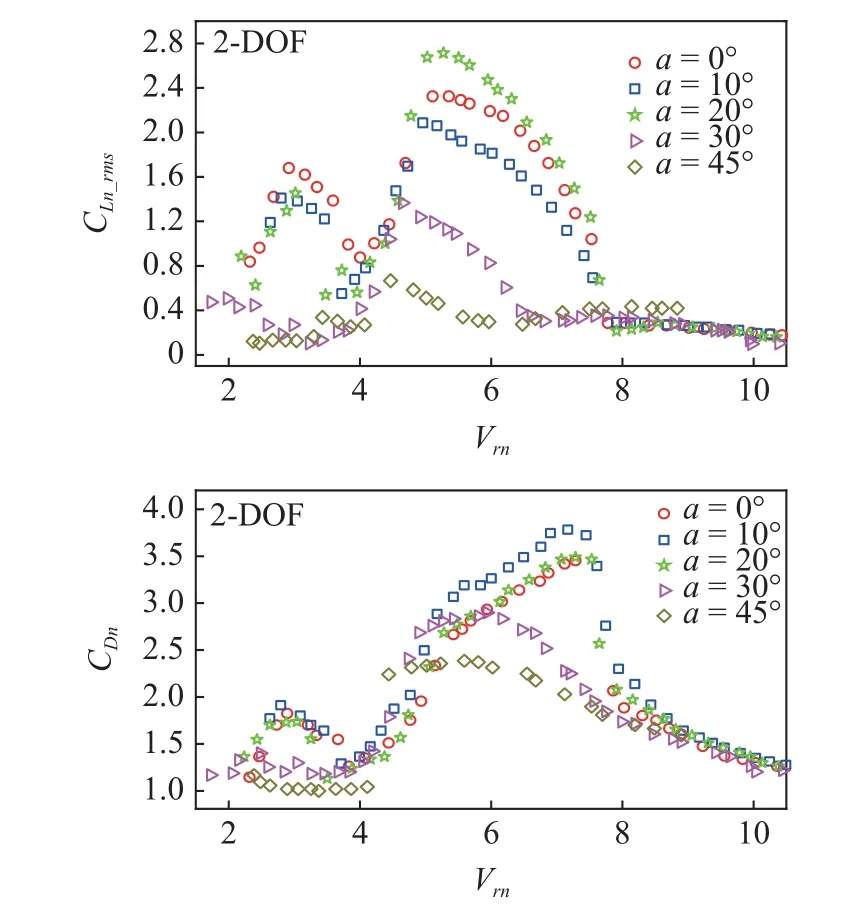
图8 倾斜刚性圆柱VIV 的流体力系数[90]Fig.8 Fluid force coefficients of an inclined rigid cylinder undergoing VIV[90]

2.4 倾斜弹性支撑刚性圆柱IP 原则适用范围

评判倾斜刚性圆柱VIV 的IP 原则适用范围需要综合考虑质量比、边界条件、自由度等多种因素影响.

对于大质量比(m*=O(103))圆柱结构,通过分析振动幅值、升力系数和相位差等结果,Nakagawa 等[84]认为倾角为45°时,IP 原则适用.至于IP 原则适用的角度上限,目前尚缺乏相关研究.对于单自由度振动的小质量比圆柱结构,最大位移、流体力系数、“锁定”区域等对应不同的适用范围.边界条件也对IP 原则的适用范围存在影响.对于边界条件影响较小的无限长圆柱结构,最大位移和“锁定”区域结果在倾角为45°时IP 原则适用[86-87];流体力系数结果在倾角超过60°后IP 原则不适用[82];IP 原则适用范围的上、下限仍不清晰.对于受边界条件影响的有限长圆柱结构,“锁定”区域结果在倾角不超过20°时适用于IP 原则[88-89].正倾角条件下,最大位移和平均阻力系数在倾角不超过10°时适用于IP 原则,升力系数在倾角不超过45°时适用于IP 原则[85,90];负倾角条件下,最大位移和升力系数在倾角不超过45°时适用于IP 原则,平均阻力系数在倾角不超过30°时适用于IP 原则[85,90].对于双自由度振动的小质量比圆柱结构,考虑边界条件的影响,振动位移、“锁定”区域、流体力系数等结果在倾角不超过20°时适用于IP 原则[90].

3 倾斜柔性圆柱VIV

3.1 振动响应

柔性圆柱结构的长径比大,结构自身可发生弯曲变形,涡激振动能够激发高阶模态.因此,倾斜柔性圆柱VIV 的振动响应特性远比倾斜刚性圆柱复杂.目前,主要研究手段为数值模拟[93-96]和实验观测[97-106].

邢国源[93]和及春宁等[94]开展了倾斜柔性圆柱VIV 的数值模拟(模型长径比为50、质量比为6.0、雷诺数为500).倾角在0°～60°时,最大振动位移结果基本接近,但振动出现多模态共存现象,振动主控模态的权重随倾角的增大不断下降,主控模态相邻模态的权重不断增大.因此,随着倾角增大柔性圆柱振动能量向更多振动模态扩散,参与振动的模态阶次增多.Bourguet 等[95]模拟了倾角为60°条件下柔性圆柱VIV (模型长径比为50、质量比为6.0、雷诺数为500),分别设置了高、低两个轴向力工况.轴向力较高时,横流向和顺流向的振动均表现为驻波特性,顺流向控制频率为横流向控制频率的二倍,运动轨迹为新月型,倾斜柔性圆柱的位移分布、响应频率与垂直圆柱的结果基本一致.降低轴向力后,振动的行波特性增强,倾斜柔性圆柱的横流向位移相比于垂直圆柱的结果降低了45%,位移的轴向分布形式也发生了显著变化.Bourguet 等[95]认为轴向力降低后圆柱的顺流向平均挠曲变形增大,原本平行圆柱轴向的来流分量在圆柱局部将产生垂直圆柱轴向的分量,正是此局部垂直圆柱轴向来流的影响使倾斜柔性圆柱的涡激振动响应与垂直圆柱的结果出现显著差异.随后,Bourguet 等[96]进一步对倾角为80°的倾斜柔性圆柱涡激振动开展了数值模拟研究.横流向和顺流向位移表现为驻波和行波混合的特性.位移的轴向分布并不对称,由于主控模态阶次不同,倾斜柔性圆柱的振动幅值与垂直圆柱也存在显著差异.

King[97]在水槽中开展了倾斜柔性圆柱的涡激振动实验,模型长径比为37,倾角变化范围为-45°～45°,雷诺数范围为2000～20 000,实验中通过测量圆柱模型中点的应变来间接获取位移信息.倾角的正、负向对响应特性的影响并不显著.倾角不超过30°时,顺流向振动较为接近;但倾角为45°时,顺流向位移更早达到极值,且最大位移显著增大.倾角对横流向振动位移影响较大,横流向最大位移增大且对应更高的等效约化速度.将柔性圆柱倾斜放置并不能抑制涡激作用,圆柱倾斜放置后增大了结构的自由长度,降低了稳定性系数和固有频率,导致VIV 更易激发.Seyed-Aghazadeh 等[102]实验研究了倾斜柔性圆柱的VIV 特性,长径比为67,质量比为0.43,雷诺数范围为320～1610,所观测的约化速度范围内振动主控模态为一阶、二阶模态和三阶模态对整体振动也存在一定的贡献.倾角为15°时,振动激发的初始约化速度、最大位移与垂直圆柱的结果一致,但轴向位移分布、位移频谱与垂直圆柱的结果仍存在差异;倾角超过15°后,振动的激发流速、前三阶模态参与权重、位移轴向分布、响应频率等结果均与垂直圆柱的结果不一致,随着倾角的增大,振动幅值有降低趋势,振动被激发的初始约化速度后移,宽频特性逐渐显著.

为了关注倾斜柔性圆柱的高阶模态涡激振动,徐万海等[100-101,103-105]开展了大长径比(350)、低质量比(1.9)、较高雷诺数(800～16 000)条件下的倾斜柔性圆柱VIV 实验研究.横流向振动最高激发四阶模态,顺流向振动最高激发六阶模态,随着倾角的增大高阶模态振动更易激发,与邢国源[93]和及春宁等[94]的数值模拟结果一致.倾斜柔性圆柱横流向和顺流向的响应频率随着等效约化速度的增大近似呈线性增长.通常顺流向响应频率为横流向的二倍,运动轨迹多为“8”字型或新月型;但倾角为45°时,某些等效约化速度工况下,顺流向响应频率大致与横流向相等,此现象在倾斜刚性圆柱VIV 实验中也存在[90],这种情况下运动轨迹为椭圆型,如图9 所示.倾角在0°～60°范围内时,Stn/St0(St0为垂直圆柱的St数)近似为1.0,进一步证实了 Zhao 等[53]的关于无限长倾斜圆柱St数的相关结论.倾斜圆柱激发高阶模态振动时,振动表现为驻波与行波的混合特性,振动位移不随倾角增大而减小,倾角超过15°后,振动位移略高于垂直来流工况的结果,且最大位移均方根在较小的等效约化速度工况即可取得极值,如图10所示.

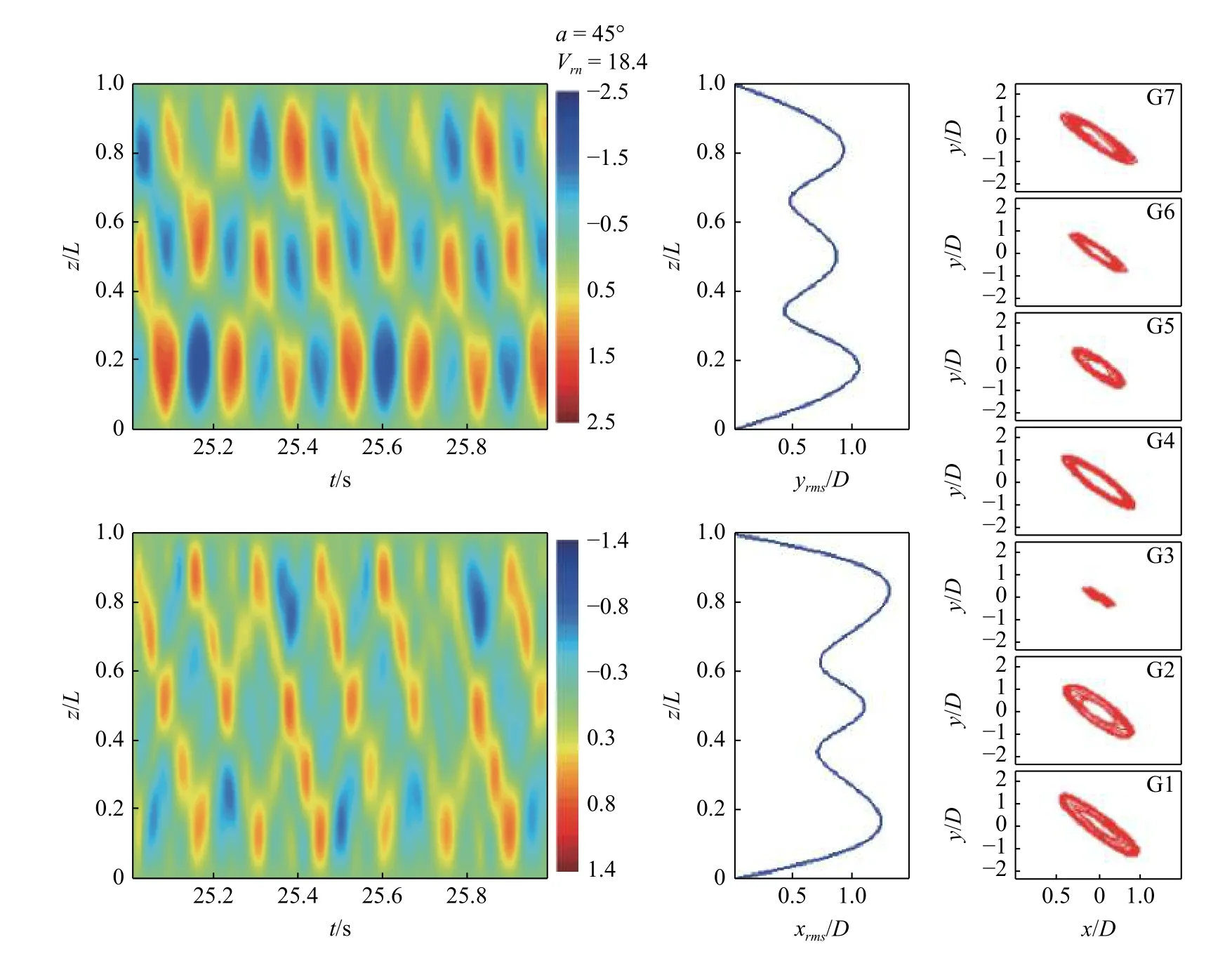
图9 倾斜柔性圆柱VIV 的位移云图、位移均方根分布和运动轨迹[104]Fig.9 Displacement contour,distribution of the RMS of the displacement,x-ytrajectory of an inclined flexible cylinder undergoing VIV[104]

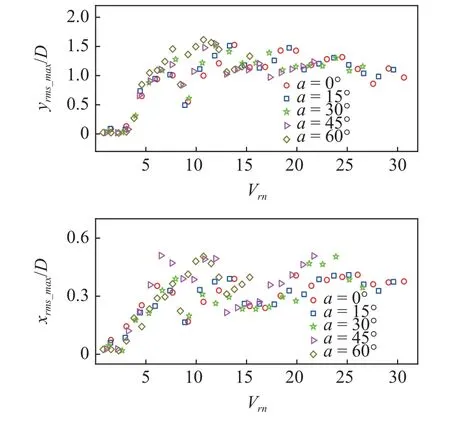
图10 倾斜柔性圆柱VIV 的振动位移[104]Fig.10 Displacements of an inclined flexible cylinder undergoing VIV[104]

3.2 尾流场特性

柔性圆柱的尾流场具有较强的三维特性,实验中难以观测,因此倾斜柔性圆柱VIV 的尾流形态主要基于数值模拟手段进行分析.邢国源[93]和及春宁等[94]研究了倾角0°～60°条件下柔性圆柱后的尾流特征,如图11所示.尾流场出现涡裂现象,尾流特性较难分辨,仅能大致归纳泻涡特征.倾角不超过30°时,尾流模式为平行交叉泻涡,且泻涡形态与振动特征一致;倾角为45°和60°,轴向流速增大,表现为倾斜泻涡模式.Bourguet 等[95]对比了倾角60°时固定刚性圆柱与柔性圆柱VIV 的尾流特性.相比于固定刚性圆柱,柔性圆柱的尾流形态更为杂乱,但形成的轴向涡线却大致与圆柱轴向平行,这与Ramberg[48]的结论基本一致.Bourguet 等[96]研究了不同轴向预张力作用下80°倾斜柔性圆柱的尾流特性.高预张力时,圆柱后的轴向涡线与圆柱轴向平行;中等预张力和低预张力时,圆柱后的轴向涡线发生偏斜,偏斜角度分别为7°和20°,当旋涡从圆柱上脱落时,呈现出较小的偏角,在近尾迹区可以看到旋涡呈弯曲状排列.徐万海等[100-101,103-105]虽然没有在实验中直接观测柔性圆柱的尾流特征,但通过St的结果,并结合Ramberg[48]的结论,可以推测得到倾角0°～60°条件下柔性圆柱发生VIV 时形成的轴向涡线大致与圆柱轴向平行,进一步证实了数值模拟研究中[95]有关轴向涡线偏斜角度的结果.

图11 倾斜柔性圆柱VIV 的尾流形态[93]Fig.11 Wake flow of an inclined flexible cylinder undergoing VIV[93]

3.3 流体力系数

柔性圆柱VIV 的流体力难以直接测量,主要通过数值模拟或者根据实验的结构响应信息重构间接确定.邢国源[93]和及春宁等[94]通过数值模拟研究分析了倾斜柔性圆柱VIV 的流体力系数,倾角在0°～60°范围内时,随着倾角增大平均阻力系数和顺流向合力系数均方根逐渐增大,横流向合力与横流向位移在圆柱轴向空间上存在相位差.Bourguet 等[95]发现倾角为60°时,倾斜柔性圆柱的平均阻力系数、顺流向合力系数均方根、横流向合力系数均方根、附加质量系数的轴向分布趋势整体上与垂直柔性圆柱的结果一致,局部位置存在一定的差异.倾斜柔性圆柱的平均阻力系数和附加质量系数有所增大.Bourguet 等[96]发现倾角为80°时,在高、中、低三种预张力水平下平均阻力系数、顺流向合力系数均方根、横流向合力系数均方根的轴向分布趋势均与垂直圆柱的结果存 在显著差异.倾斜柔性圆柱的平均阻力系数、顺流向合力系数均方根、横流向合力系数均方根显著增大.

徐万海等[103-105]基于实验中观测的倾斜柔性圆柱VIV 响应信息重构了圆柱受到的流体力,并将横流向和顺流向的流体力合力进行分解得到了升力系数、脉动阻力系数和附加质量系数.由于数值模拟研究中计算效率较低,仅能选取个别流速工况分析流体力系数结果.通过逆向重构流体力的方式,给出了倾斜柔性圆柱由低阶模态振动向高阶模态转化全过程中流体力系数变化情况[103-105].

对于横流向合力系数均方根,倾角为15°和30°时,随等效约化速度的变化趋势与垂直圆柱的结果基本一致,仅在个别等效约化速度工况下,存在较小的差异,这些差异主要是振动位移之间的差异导致的;倾角为45°时,在一阶模态范围内和二阶模态范围的前半段,横流向合力系数均方根显著增大;倾角为60°时,VIV 激发后,横流向合力系数均方根显著增大.倾角对顺流向脉动合力系数均方根的影响较为复杂.倾角为15°和30°时,顺流向脉动合力系数均方根随等效约化速度的变化趋势与垂直圆柱的结果基本一致;倾角为45°时,顺流向脉动合力系数均方根在等效约化速度4.3～11.9 范围内波动变化,在等效约化速度13.0～18.4 范围内较为稳定,整体低于垂直圆柱的结果,等效约化速度超过18.4 后,顺流向脉动合力系数均方根开始增大;倾角为60°时,顺流向脉动合力系数均方根极值显著增大.

倾斜柔性圆柱的平均阻力系数在倾角超过30°后并未随倾角的增大而减小,而是显著增大,这与倾斜刚性圆柱VIV 的结果不同[90],与倾斜柔性圆柱VIV 的数值模拟结果一致[96].倾斜柔性圆柱的平均阻力系数与横流向位移具有一定的相关性,考虑倾角拟合了平均阻力系数与最大横流向位移均方根的经验公式

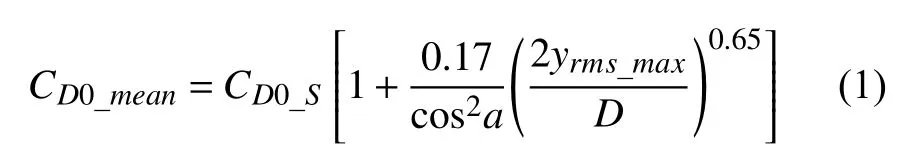
式中,CD0_S为静止圆柱的平均阻力系数,可取为1.2.通过式(1)可以近似估计倾斜柔性圆柱VIV 的平均阻力系数.

对于升力系数,倾角为15°时,随等效约化速度的变化趋势整体与垂直圆柱一致;倾角为30°时,由于倾斜圆柱更早进入高阶模态,在模态转化阶段升力系数高于垂直圆柱的结果;倾角为45°和60°时,升力系数显著增大.脉动阻力系数随倾角的变化规律较为复杂,倾角为45°和60°时,脉动阻力系数的结果与垂直圆柱相比差异显著.对于附加质量系数,倾角为0°～60°时,随等效约化速度的变化规律一致,但由于大倾角情形下圆柱振动易激发高阶模态,倾角为45°和60°时,附加质量系数增大的时机提前,如图12 所示.

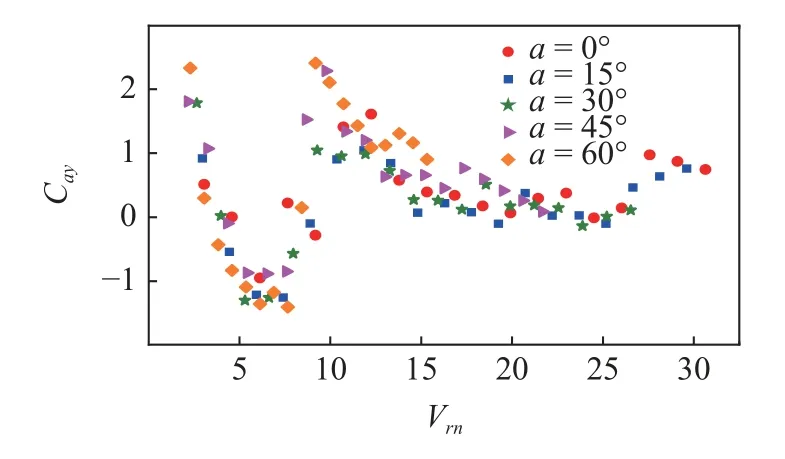
图12 倾斜柔性圆柱VIV 的附加质量系数[104]Fig.12 Add mass coefficients of an inclined flexible cylinder undergoing VIV[104]

3.4 倾斜柔性圆柱IP 原则适用范围

倾斜柔性圆柱的VIV 特性多变,分析IP 原则的适用性时需要综合考虑响应规律和流体力特征.

涡激振动响应规律方面,需要综合考虑倾角对控制频率、主控模态、振动位移等多种指标的影响.倾角不超过15°时,控制频率、主控模态、最大位移均方根随等效约化速度的变化趋势、位移的时频特性、运动轨迹等均与垂直来流工况的结果一致,IP 原则适用.倾角15°～30°时,控制频率、位移的时域及频域特性、运动轨迹与垂直来流工况的结果较为一致,虽然主控模态和最大位移均方根随等效约化速度的变化趋势与垂直来流工况的结果存在一些差异,但整体差异并不显著,可认为IP 原则基本适用.倾角超过30°后,控制频率、主控模态、最大位移均方根随等效约化速度的变化趋势、位移的时域及频域特性、运动轨迹与垂直来流工况的结果存在显著差异,IP 原则不完全适用[104].

流体力特征方面,需要综合考虑横流向和顺流向脉动合力系数、平均阻力系数、升力和脉动阻力系数、附加质量系数.倾角为15°时,大多数流体力特征与垂直来流工况的结果一致,但某些等效约化速度工况下,平均阻力系数、流体力系数的轴向分布仍与垂直来流工况的结果存在一定的差异;倾角为30°时,多种流体力系数随等效约化速度的变化规律与垂直来流工况的规律一致,但相同等效约化速度下,流体力系数的数值和轴向分布可能与垂直来流工况的结果存在偏差;倾角为45°和60°时,流体力特征与垂直来流工况下流体力特征之间的差异显著增大,多种流体力系数随等效约化速度的变化规律发生变化,流体力系数的数值普遍偏高,流体力系数的轴向分布形式显著不同.因此,从流体力角度,当倾角超过30°后,IP 原则不再适用[105].

4 倾斜圆柱VIV 抑制

圆柱结构VIV 抑制主要是基于干扰流场的方式实现.根据不同的机理,VIV 抑制装置可分为三类[107]:

(1)表面凸起型,如螺旋列板、表面凸起等,其原理是通过影响分离线或分离剪切层;

(2)裹覆型,如控制杆和轴向板条等,原理是通过影响卷吸层来抑制旋涡的形成和脱落;

(3)近尾流稳定器型,如整流罩和分离板等,其原理是阻止卷吸层的相互作用以影响尾流结构和涡脱落形态.

大多数表面凸起型和裹覆型抑制装置,具有全向性,即对各个来流方向均能起到较好的抑制效果.近尾流稳定器型抑制装置的抑制效率对来流方向具有较强依赖性,这类抑制装置仅在个别方向的来流工况发挥较好的抑制效果.目前,分离板、整流罩、螺旋列板和控制杆是常用的VIV 抑制装置,在垂直来流作用下这些装置已得到了较多关注.但当来流与圆柱轴向不垂直时,VIV 抑制装置的抑制效果仍有待研究.目前,关于倾斜圆柱VIV 抑制的研究十分有限,已有研究中关注了螺旋列板和控制杆这两类抑制装置.

4.1 螺旋列板

螺旋列板凭借在垂直来流作用下圆柱涡激振动控制效果好、成本低廉等优点,其对倾斜圆柱结构VIV 的抑制效果得到了优先关注[108-114].

Zeinoddini 等[108]实验研究了螺旋列板对倾斜刚性圆柱VIV 的抑制效果.仅允许结构横流向振动,螺旋列板的螺高/螺距为0.1D/10D.倾斜圆柱安装螺旋列板后,最大振动位移随倾角的增大而降低.倾角为0°,20°和45°时,螺旋列板对最大振动位移的抑制效率分别为54%,51%和62%.在“锁定”区的开始阶段,倾角对螺旋列板的抑制效率影响较小;在“锁定”区后半段(等效约化速度超过7.5),倾角为45°时螺旋列板的抑制效率急剧下降,甚至出现负值,此时安装螺旋列板后振动反而增强.产生这种现象的主要原因是: 随着流速增大轴向流作用进一步增强,倾斜圆柱安装螺旋列板后轴向流还会出现较强的旋转.因此,对于安装螺旋列板的倾斜圆柱结果,来流的轴向分量产生的影响不能被忽略.

徐万海等[109-114]开展了一系列模型实验,系统地研究了螺旋列板对倾斜柔性圆柱VIV 的抑制效果.螺旋列板的螺高/螺距为0.25D/17.5D,螺头数为3 根,这组螺旋列板参数在垂直来流作用下对柔性圆柱VIV 的抑制效果优异[115].安装螺旋列板后,倾角对柔性圆柱的响应频率、响应模态和振动位移影响显著.对于响应频率,倾角为0°时,响应频率被显著抑制;倾角为15°时,响应频率在一定程度上被抑制;倾角为30°和45°时,响应频率并未被有效抑制.垂直来流作用下螺旋列板作用显著,原来有规律的涡激振动被扰乱;倾角为45°时,圆柱的振动仍非常有序.垂直来流作用下,安装螺旋列板后圆柱的最高激发模态由四阶降低至二阶;但倾角为15°～45°时,圆柱仍能激发三阶模态振动.

对于横流向振动位移,倾角为0°时,安装螺旋列板后最大位移均方根一直保持在较低水平,多数流速工况下不超过0.10D;倾角为15°,30°和45°时,螺旋列板抑制效果减弱,最大位移均方根分别为0.44D,0.38D和0.76D.随着倾角的增大,螺旋列板的抑制效率急剧下降,倾角为0°,15°,30°和45°时,平均抑制效率分别为91.3%,79.3%,76.7%和49.4%,如图13所示.对于顺流向振动位移,倾角为0°时,安装螺旋列板后最大位移均方根不超过0.04D;倾角为15°,30°和45°时,最大位移均方根分别为0.12D,0.09D和0.28D.螺旋列板对顺流向振动的抑制效率受倾角影响极大,倾角为0°,15°,30°和45°时,平均抑制效率分别为94.8%、82.6%,76.9%和23.9%.特别是倾角为45°时,某些流速工况下,抑制效率接近于0,安装螺旋列板对顺流向振动位移并无抑制作用.

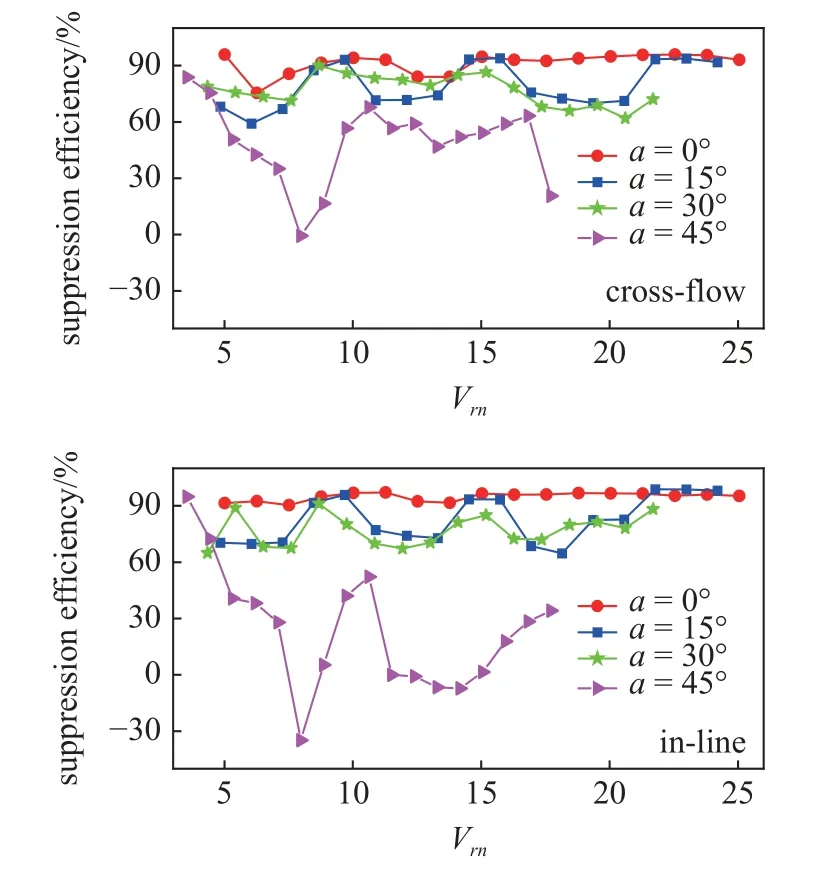
图13 螺旋列板的抑制效率[111]Fig.13 Suppression efficiency of helical strakes[111]

4.2 控制杆

控制杆通过影响绕流边界层的发展,达到抑制振动的目的.控制杆的布置可充分利用主圆柱结构周围的附属小圆柱,具有极其广阔的工程应用前景.一些学者通过数值模拟和模型实验研究了垂直来流作用下控制杆个数、间距、布置形式等因素对圆柱VIV 抑制效果的影响[116-120].而控制杆对倾斜圆柱涡激振动抑制效果的研究相对较少[121].

徐万海等[118-121]通过模型实验系统地研究了控制杆对柔性圆柱VIV 的抑制效果.控制杆的个数为三根或四根、外径为0.25D、控制杆外表面距圆柱外表面的距离为0.5D,安装角度设置多种工况.对于垂直柔性圆柱,控制杆个数和安装角度对抑制效果影响显著.安装角度分别为0°,20°,40°和60°时,三根控制杆的抑制效率分别为40%,57%,71% 和70%;安装角度分别为0°,15°,30°和45°时,四根控制杆的抑制效率分别为60%,80%,85%和90%.四根控制杆的抑制效果整体优于三根控制杆[118-120].在上述研究基础上,进一步研究了四根控制杆对倾斜柔性圆柱VIV 的抑制效果[121].

控制杆对倾斜柔性圆柱响应频率的抑制作用受倾角的影响较小,倾角为45°时倾斜圆柱的响应频率与垂直圆柱的结果十分接近.安装控制杆后,倾斜柔性圆柱的主控模态也并未受到控制杆的显著影响.无论对于垂直圆柱还是倾斜圆柱,控制杆对横流向振动位移的抑制效率随等效约化的增大而提高,且安装角度为45°时抑制效率最高.对于安装角度为45°的控制杆,随着等效约化速度的增大倾角为0°时的抑制效率可达90%;倾角为45°时的抑制效率可达80%,如图14 所示.由于实验观测的流速工况有限,根据抑制效率的变化趋势可以推测,抑制效率仍会随流速的增大而提高.控制杆对顺流向振动位移的抑制效果也随流速增大而提升.安装角度为45°工况下,随着等效约化速度的增大,倾角为0°和45°时的抑制效率均可达到90%.因此,在合理布置控制杆后,控制杆对垂直圆柱和倾斜圆柱均能发挥优异的抑制效果.

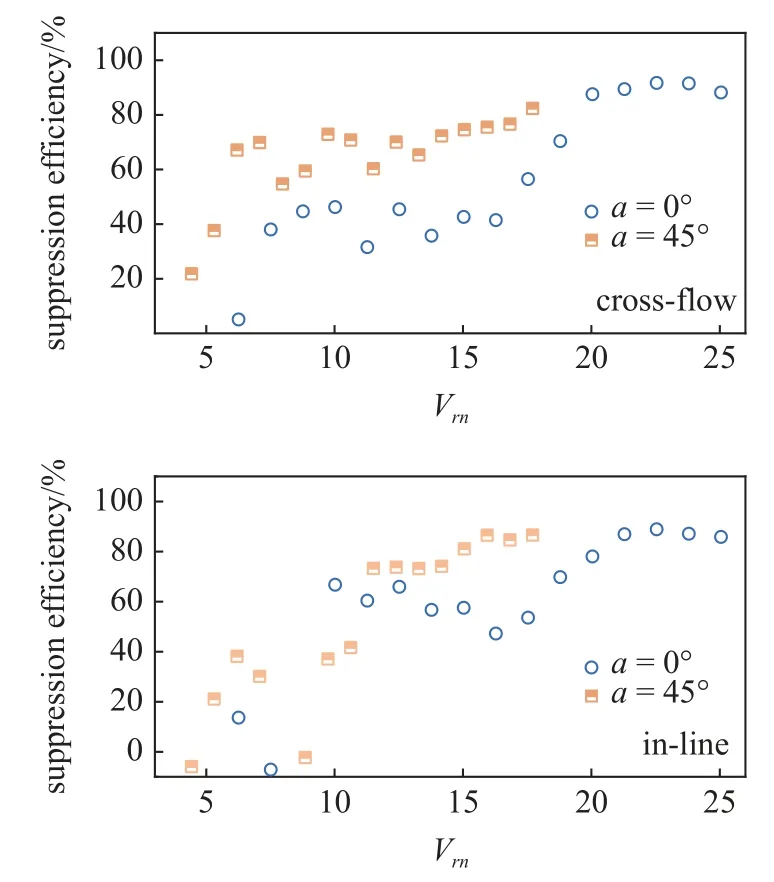
图14 控制杆的抑制效率[121]Fig.14 Suppression efficiency of control rods[121]

5 结语与展望

圆柱结构涡激振动是工程中的一种十分常见的现象,其严重威胁结构安全.实际上,由于来流方向并不总是与结构轴向垂直,倾斜圆柱的涡激振动更为普遍.本文回顾了近年来关于倾斜圆柱涡激振动的研究工作,总结了在“固定倾斜圆柱结构绕流”、“弹性支撑倾斜刚性圆柱结构涡激振动”、“倾斜柔性圆柱结构涡激振动”和“倾斜圆柱结构涡激振动抑制”四个方面的研究进展.

(1)关于固定倾斜圆柱绕流的研究较多,在斯托罗哈数St、尾流场特性和流体力系数等方面已达成较多的一致性结论.影响IP 原则适用范围的主要因素为雷诺数和边界条件.St主要受圆柱轴向涡线偏斜角度的影响,轴向涡线与圆柱轴向平行时St适用于IP 原则.平均阻力系数通常在倾角不超过30°时适用IP 原则.

(2)弹性支撑倾斜刚性圆柱的涡激振动特性主要受质量比、自由度和边界条件的影响.大质量比圆柱结构在倾角为45°时IP 原则仍适用.小质量比单自由度(横流向)圆柱结构在不考虑边界条件影响时,IP 原则适用范围较大;考虑边界条件影响后,IP 原则适用范围急剧缩小.考虑边界影响,小质量比双自由度结构在倾角不超过20°时IP 原则适用.

(3)倾斜柔性圆柱的涡激振动特性更为复杂.综合考虑倾角对涡激振动响应和流体力的影响,倾角不超过15°时,主控模态、振动位移、流体力系数等与垂直圆柱的结果基本一致;倾角在15°～30°之间时,主控模态、振动位移、流体力系数等结果的变化规律与垂直圆柱一致,但某些工况时数值上存在差异;倾角超过30°后,主控模态、振动位移、流体力系数等的变化规律发生改变.因此,倾角不超过30°时,IP 原则适用.

(4)倾斜圆柱涡激振动抑制方面的研究较少,关注较多的抑制装置是螺旋列板和控制杆.螺旋列板的抑制效果随倾角的增大而变差,倾角45°时抑制效率急剧降低.控制杆的抑制效率受倾角的影响较小,且随流速增大而提高.

本文在回顾与总结中发现: 倾斜圆柱结构涡激振动方面仍存在一些问题有待进一步解决.倾斜刚性圆柱与倾斜柔性圆柱实验结果之间存在某些由于边界条件导致的差异,边界条件对倾斜圆柱涡激振动的影响值得深入探讨;柔性圆柱VIV 尾流的三维特征显著,目前关于倾斜柔性圆柱尾流场分析多基于数值模拟方法,有待借助三维流场显示技术观测尾流特征;柔性圆柱VIV 的流体力多基于流体力重构方法间接获得,有待借助先进传感器测量倾斜柔性圆柱VIV 的流体力,深入分析流体力特性;目前主要关注了单根倾斜圆柱涡激振动,实际工程中圆柱结构多以柱群的形式存在,圆柱之间的相互干涉使问题更加复杂,倾斜柱群涡激振动特性的研究也亟待开展.