条条大路通罗马，一题多解辨最优——解三角形中的最值问题

庞启满，张祖兰

(南宁市第三中学，广西南宁，530021)

《普通高中数学课程标准(2017年版)》指出，最值是函数内容中重要的性质之一，要求学生能用符号语言表征函数的最值，并理解函数最值在实际生产与生活中的作用与实际意义[1].与此同时，最值也是高考的高频考点.三角函数、不等式、导数等高中数学的重点内容都可以联合最值加以考察.要想解决最值问题，学生需要充分理解并且综合地运用数形结合、函数与方程、化归与转化等多种思想方法.这些思想方法有助于锻炼学生数学学习思维，也有利于培养学生形成问题解决的策略.掌握这些思想方法是学生形成核心素养的重要途径.

在最值问题的教学中，教师们要以落实核心素养为导向，以避免迷失在偏题、怪题等的教学与训练中[2].因此，本文以解三角形为研究载体，研究此类问题的通法通解.

1 非对边对角中的最值

例1若a,b,c为锐角三角形A,B,C的对边，且sin2B+sin2C-sin2(B+C)=sinBsinC.

(1) 求角A；

(2) 若b=2，求△ABC面积的取值范围.

解：(1) ∵B=π-(A+C)∴sin(B+C)=sinA；

方法一 余弦定理列方程

求边长c的范围，可以借助余弦定理表述出三角形的边角条件，运用方程与不等式的思想求解c的范围.

由a2=b2+c2-2bc·cosA得，a2=c2-2c+4. ①

在解题后，不仅要检验过程与结果，更要回头体会方法一中的函数与方程思想.解法一是以运动与变化为出发点，在动态中抓住不变量，通过分析将题目条件—锐角三角形转化成不等量关系，并建立函数、方程与不等式，从而解决问题.解法二中也充分体现出这一思想方法，读者要注意体会.

方法二 正弦定理边化角

由于三角形内角有限制范围，因此可以选择运用正弦定理将c边转化成角C的表达式，将问题转化成在给定角度范围内三角函数的最值问题，从而再求解.

∵△ABC为锐角三角形，

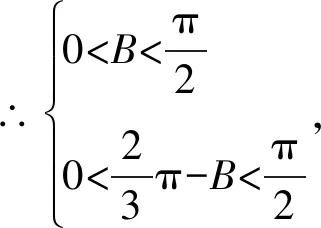
在方法二中我们一起体会了转化与化归的魅力.数学教育家布卢姆曾说：转化思想就是“把问题元素从一种形式向另一种形式转化的能力”[3].当解决问题受阻时，我们需要观察问题的本质，思考分析如何将所学知识与能力水平与待解决的问题建立联系，将复杂的问题简单化，将陌生的问题熟悉化，从而将问题转化成较易求解的问题.在求解新问题后，翻译并得到原问题的解答.

方法三 直观想象探范围

角C和边b是固定不变的，因此我们借助图形观察点B运动的轨迹，以动态的思维去找寻锐角的临界位置.

当点B在线段B1B2上从左往右运动时，S△ABC越来越大，

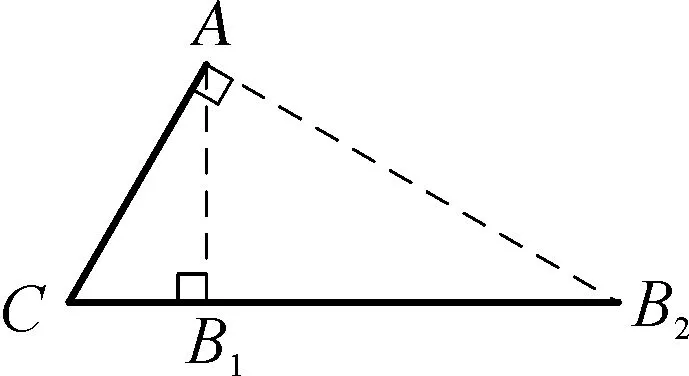
图1

可以看到，直观想象是借助数形结合进行问题转化的核心素养.在解题中，以形助数，以数辅形，借助图形直观地呈现问题本质，形象静态地呈现运动规律，从而达到优化解题之效.

综上可知，要想突破解三角形中的最值问题，需要学生深刻理解并且综合地运用正余弦定理进行边角表达与转化.在上述三种解法中，学生不仅需要牢固地掌握正余弦定理，也深刻体会到转化与划归、函数与方程思想，感受到数学知识之间的紧密联系；逻辑推理、数学运算、直观想象等核心素养得以锻炼而提高，而这也正是《普通高中数学课程标准(2017版)》的要求.

掌握了正余弦定理，就可以解决简单的三角形度量问题.而在三角形中，除了面积外，边长、周长以及特殊的线段范围都是常见的最值问题.

变式1在例题的条件下，求△ABC周长的范围.

方法一 余弦定理造函数

由于周长就是三边之和，因此可以直接运用余弦定理找寻边长关系，运用消元的方法构造出以边c为自变量的函数，从而将三角形周长的最值转化成函数的最值，运用函数知识解决问题.

方法二 正弦定理边化角

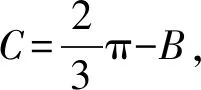
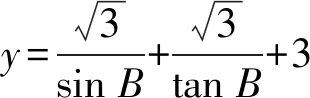
方法三 直观想象探范围

我们同样可以结合题目条件与数据，作图直观呈现出点B运动中周长的变化趋势，从而获得周长的范围.

我们可以发现给出的角A与边b不是对角与对边的关系时，可以灵活地选择正弦定理将问题转化成三角函数的单调性问题；也可以选用余弦定理构造出有关边长的函数，再求解此函数的单调性.选用正弦定理或者余弦定理的过程虽然大不相同，但是思想一致，在解决问题的过程中尽可能根据三角形的边角关系进行消元，构造出函数问题，将所求的问题转化成函数的值域问题.

3 对边对角中的最值

在解决完问题之后，一定要及时地反思与回顾，进一步地思考与探究.那么如果给出的是对边与对角的关系，上述思想方法是否还适用？现代学习理论认为有意义的学习都是在原有的认知基础上迁移而得的.在经历综合运用正余弦定理综合解决非对边对角的问题之后，学生不仅要掌握此类问题，还要学会将解题过程中的思想方法与部分的解决结论迁移到对边对角类型中，通过比较分析不断同化问题，构建稳定的认知结构，提升认知水平与逻辑能力.

解：

按照前面的思维过程，我们先考虑是否可以运用余弦定理表示找寻边长关系进而求解.

又由余弦定理可得，a2=b2+c2-2bccosA，即4=b2+c2-bc.

观察代数式的结构，利用基本不等式进行放缩，即可以求出bc的范围，b2+c2-bc≥2bc-bc=bc，故bc≤4.

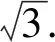
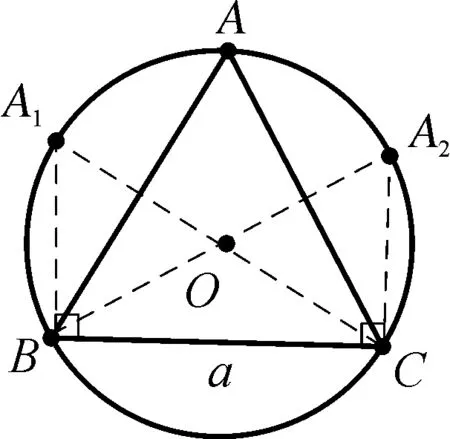
图2

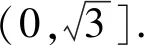
若是题目对三角形的形状有限制，那么面积又在什么范围呢？

在变式2的解答中，我们运用余弦定理，结合基本不等式的代数计算技巧求出面积的最大值，但是无法以同样的思想求出最小值.那么现在我们可以结合图形分析三角形面积的范围.

解：方法一 余弦定理求范围

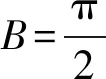
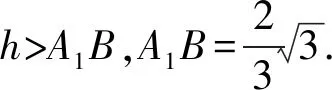
方法二 正弦定理边化角

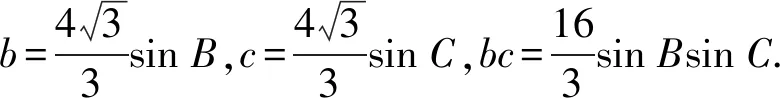
结合已有的解决问题的经验，不难想到下一步是要消元，将问题转化成求给定区间上的三角函数最值问题.

此时，需要对式子降幂，

又∵△ABC为锐角三角形，

方法三 直观想象探范围

图3

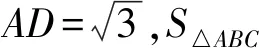
考虑到锐角△ABC中，角度的范围任意表示，这里采用正弦定理将边转化成角，这样容易表示变式中的条件与结论；而角度的限制不容易转化成线段之间的关系，故在条件变式4中，笔者采用正弦定理示范解答.

解：由正弦定理可以得到，

总结：当所给的边角关系不是对边与对角关系时，或者给出的锐角三角形，运用正弦定理将问题转化成角度，这样有利于解决问题.如果给的是对边与对角，则可以在余弦定理的基础上灵活运用基本不等式进行解答.

如果题目进一步限制三角形的形状时，由于角度的范围容易求得，故用正弦定理将边长转化成角度，更加有利于解决问题.

当我们能综合地运用正余弦有关知识解决三角形面积与周长的问题之后，我们不妨思考：这些方法策略还能解决三角形中的哪些问题呢？三角形中还有三条重要的线段：角平分线、中线与高，那么如何刻画这些线段的范围呢？

解：方法一 向量模长求线段

此式中出现两个正数的和与积的结构，不难想到运用余弦定理进行消元，基本不等式求范围.

当然，作图数形结合也可以解决.

方法二 直观想象探范围

图4

由于中线位置特殊，此时我们可以考虑引入向量，借助向量的模长刻画线段的长度.

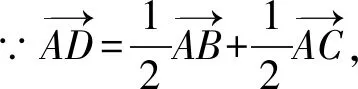
由余弦定理得，c2+b2=4+bc≥2bc，解得bc≤4，当且仅当b=c=2时，等号成立.

图5

此时，读者可以考虑在统一条件下的△ABC中高AD又在何范围呢？

4 提炼总结

本文对高中阶段解三角形中常见的最值问题按照非对边对角与对边对角两大类型以丰富的变式对三角形的性质如面积、周长、重要线段进行了全面而深入的解法研究.可以看到，正弦定理与余弦定理是解决三角形最值问题的强有力工具，我们需要灵活地运用正余弦定理进行边角转化，将三角形的问题转化成函数特别是三角函数的最值问题，这既是求解三角形最值的通法；也是复杂的三角形问题如要求三角形为锐角三角形的优解.当然，通过作图表征出三角形特点并直观想象，探索规律也是很好用的办法.在本文中，笔者从余弦定理列方程、正弦定理边化角、直观想象探范围等三个思想方法一题多解，进行解法拓展，目的是使得学生在掌握每种类型的相应解法的同时又不囿于解题通法，锻炼学生的逻辑思维.

5 教学启示

在笔者看来，讲授三角形最值最重要的是引导学生感悟上述的思想方法，剖析清楚上述思想方法在解决此类问题中发挥的作用与意义，这样学生才能领悟思想本质，形成解三角形的方法策略.当然，题目是思想方法的载体，教师要精心挑选典型例题进行精讲，由浅到深，层层深入归纳出解三角形最值问题的通法通解，总结出解题模型.再辅以适当的变式训练，努力做到深入浅出.在课上给予学生充分练习的时间，鼓励学生积极思考、主动探究最值问题的本质，塑造学生在相应题型中实用高效思维模式，以便学生能掌握并运用有关知识；通过螺旋式教学培养学生的迁移能力，提升学生的思维水平.