沟通本质联系， 建构知识星座——《分数的加法和减法》教学思考与实践

江成刚

(苏州市吴江区盛泽实验小学，江苏苏州，215228)

数学知识虽然在教学中被分成一个个知识点逐个学习，但它们并不是孤立的，而是互联互通一脉相承的.但现实中往往存在这种现象，老师只注重了一节内容的精心设计、目标落实，却忽略了从一个更宏观的角度和更高远的视野来进行教学，以体现数学知识间的相互联系，突出知识本质.数学知识点很多，如天上的星星，如果在教学中不对相关知识进行归纳整理、建构组织，使它们形成体系和框架，那么数学学习将是低效的，学生必将被繁纷复杂的知识点所困扰.或许天文学家的做法能给我们启示，根据星星之间的联系和特点把原本孤立散乱的星星编成一个个星座，使之产生联系.这样虽然星星数目众多，但从星座的角度去观察就显得井然有序、生动活泼.

那么根据数学知识间的本质联系、思想方法等统领数学知识的主线也构建出数学知识的“星座”，将大大提高教学有效性.学生才能在庞杂的数学知识中找出本质联系，才能深刻理解和灵活运用所学知识，真正掌握数学思想方法的精华.要突出知识间的联系和本质，建构出数学知识点之间的“星座”，就要将一些形式相似、本质一致或联系紧密的知识点组织在一节课或连续的几节课中进行系统性教学，形成知识体系，做到前有孕伏，中有过渡，后有总结.

人教版五年级下册数学教材中，把“分数的加法和减法”分为“同分母分数加、减法”和“异分母分数加、减法”，用两个课时来分别教学.先是“同分母分数的加、减法”教学和相关练习，接着是“异分母分数的加、减法”教学和相关练习.这样分为两个课时进行新知学习并紧跟练习，学习容量小难度低，学生容易掌握.但分析教材发现这种安排方式也有一定的不足之处，同分母分数的加、减法内容简单，学生通过自学都能很好地掌握，如果专门用一个课时来教学，没有挑战性，探究性不强.异分母分数的加、减法是建立在同分母分数加、减法和通分、约分的基础上的，学生已经掌握了通分、约分，同分母分数加、减法又很简单，所以对异分母分数的加、减法掌握也比较容易的，如果将这种简单的内容按知识结构分开进行“小步子”教学，再进行练习巩固，虽然容易掌握，但学生不能从整数、小数、分数这一整体来看待运算知识，不利于学生深刻理解加、减法运算的意义和原理，更不利于学生探索能力的发展.

如果从知识本质出发，把计数单位、位值制和整数、小数、分数加减法整合在一起，建构出“知识星座”，让学生把这些运算知识联系起来，然后在整数和小数加减法中进行比较探索，得出加减法运算的本质，即加、减运算其实就是相同计数单位的个数相加、减.有了这种认识之后，再引导学生将加、减法运算的本质运用于分数之中，学生就能掌握知识本质，更深刻地理解分数加、减法背后的思想方法，而不是仅仅掌握运算技能，同时在比较探索中发展了学生探索能力、推理能力和迁移能力.这样把这些知识整合在一起，增强了挑战性，而且处于学生最近发展区，给学生跳一跳的动力和兴趣.

基于以上的思考和认识，进行了如下的教学尝试.

1 做回小老师，探寻错因

师：下面是低年级学生做的题目，你们当一回小老师，先观察判断是否正确，如果错误请找出错误原因并修改.

出示题目：

第一题：12.5+3.79=5.04和7.16-3=7.13的竖式.

第二题：31米长的绳子，用去11分米，还剩多长？

学生做法：31-11=20(分米)

学生观察分析，完成纠错，并汇报

生：第一题中，第一个竖式错误，小数加法中末位不能对齐，小数点应该对齐.

生：第二个竖式中3应该和7对齐，个位和个位对齐.

生：第二小题中不能用31减去11，应该先把单位化统一，再减.

师：第一个竖式中把小数点对齐之后，7和5就对齐了，7和5分别在什么位置？它们分别表示多少？

生：7和5都在十分位，7表示7个十分之一，5表示5个十分之一.

师：5和7的计数单位是多少？

生：十分之一.

生：12.5中的5的计数单位是十分之一，3.79中的9的计数单位百十分之一，5和9不能直接相加，5加9等于14，那到底是14个十分之一还是14个百分之一不能确定.

生：计数单位相同时才能直接相加.

师：那么把小数点对齐后，其实就是把什么对齐了？

生：把相同数位对齐了.

师：第二小题里面31和11为什么不能直接减？

生：它们的单位不相同.

总结规律：整数和小数加、减法要用相同计数单位的数字直接加、减，在问题解决中也要用相同数量单位的数字相加、减，不同数量单位不能直接加减.

【设计目的】：先给学生呈现一组低年级学生常出现的错题，让学生做一回小老师，这样的引入方式给了学生表现自身价值的机会，符合学生心理，能调动学生的积极性.通过对三个算式的分析和纠正，让学生领悟整数和小数加、减法法则的本质是一致的.此环节巧妙地沟通了整数、小数加减运算、位值制、计数单位等运算知识之间的联系，唤起学生已有经验，让新知识的学习与旧知识建立联系，为学生探索本课重点做好铺垫.

2 引入主题，探索新知

2.1 探索同分母分数加、减法

师：整数和小数加、减法中都是把相同计数单位的数字进行加、减，那分数加、减法是否也遵循这一规律呢？

(学生展开猜测和推理，有的说是有的说否.)

出示同分母分数加减法题目：

学生尝试计算，并说明自己的理由.

生：可以直接计算，因为分母相同意味着分数单位相同.

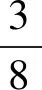
师：结合事例说说.

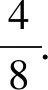
总结法则：同分母分数相加、减，分母不变，只把分子相加、减.

(2) 探索异分母分数加、减

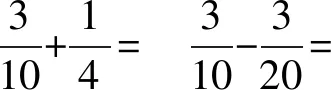
师：这两道算式与刚才的两道有什么不同？

生：上面两个分母相同，是同分母分数加、减法，这两个分母不同，是异分母分数加、减法.

师：那当分数单位不同时，我们可以直接进行加、减运算吗？

生：不能.

师：分数单位不相同就不能直接相加减，那怎么办呢？

生：可以先通分.

师：那通分的作用是什么？

生：其实就是把分数单位变相同，分数单位相同了就可以直接加了.

(课件出示)

总结法则：异分母分数相加、减，先通分，然后按照同分母分数加、减法进行计算.

【设计目的】：通过前边对整数加减、小数加减、位值制、计数单位等运算知识的沟通，学生在纠错和交流中更宏观地理解了它们之间的本质联系.学生就能理清串联这些知识的无形的“线”，就能用这些知识构建起一个“知识星座”.这根无形的“线”就是“加、减运算其实就是相同计数单位的个数相加、减”，即加减法原理，而整数加减、小数加减、位值制、计数单就是这个“星座”上的一颗颗“星星”.那么，接下来就自然而然地将分数加减法也串联在这根“线”上，镶在这个“星座”上，较好地实现了知识迁移，突出了知识本质.