同构方程视角下高中数学解题思考
——以解析几何试题为例
朱加义
(宁波市甬江职业高级中学,浙江宁波,315000)
解析几何在高中阶段是一个非常重要的数学内容,其特点在于运用代数的方法研究几何图形的几何性质,可以渗透丰富的数学思想方法,可与代数、三角、向量等知识相联系,同时也是高考重点考查的内容.解析几何大题中,主要考查一定点、两直线、斜率和与积、相切等内容.当这些命题元素以不同的形式组合时,就成就了现代高考,高考题不能不计算,合理的计算有着某种次序和某种安排.在本文中,笔者要揭开的这序就是同构式.
1 熟悉知识背景 了解方法本质

2 探究典型例题 把握解题方法
题型一 双切圆同构
例1(2011·浙江理)已知抛物线C1:x2=y,圆C2:x2+(y-4)2=1的圆心为M,P是C1上一点(异于原点),过点P做圆C2的两条切线,交C1于A、B两点,若MP⊥AB,求PM的方程.
分析:本题涉及到圆的两条切线,如果尝试去求出A、B两点的坐标,再算出kAB,那么将会涉及到非常大的计算量.进一步分析,可以考虑利用切线与圆相切,圆心到直线距离等于半径之一隐含条件来构造同构式,但如何合理表示出切线方程是关键.实际上,往往可以利用韦达定理,反向表示出两条切线的方程.

点评:反向表示PA、PB方程是关键.实际上,抛物线x2=2py与直线l交于A、B两点,为了得到同构方程,把AB方程表示(xA+xB)x-2py-xAxB=0是解题的关键.
题型二 平行弦的点式同构

分析:本题欲求直线AB在y轴上的截距,可以尝试先写出直线AB的方程.事实上,设A、B两点坐标,利用向量之间的关系,表示出C、D两点坐标,代入椭圆方程,不难构造出同构式.

点评:本题同构式,设A解C,设B解D.由于比值相同,交于同一点,同构关系非常明显,最后由A、B满足同一个同构式,直接求出AB方程.
题型三 切线同构
例3设点P为直线y=x-3上的动点,过点P作抛物线x2=2y的两条切线,切点为A、B,证明:直线AB过定点.
分析:本题实际上是考察阿基米德三角形中切点弦的过定点问题.题目同样涉及到抛物线的两条切线,我们同样构造同构式,表示出切点弦的直线方程.这里实际并不需要联立直线和曲线方程来构造同构式,因为抛物线任一点的切线斜率和该点坐标是有关的.
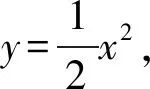
点评:本题巧设P点坐标,构造同构式,写出切点弦的直线方程,又设而不求,方法巧妙,计算量小.
题型四 斜率同构

分析:首先易得双曲线的方程,接下来考虑设直线方程,两次联立直线与曲线,利用点在直线上,构造关于kAM,kAN的同构式,利用kAM+kAN=0求解.


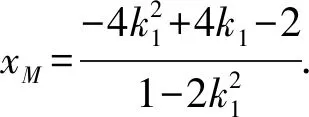
点评:如果通过直线曲线联立,运用韦达定理设线特点,直接带点进行计算,其计算量是相当惊人的,在这里,我们直接构造关于k1、k2的同构式,整体运用k1+k2,k1·k2,使得计算逻辑清晰且计算量大大降低.
题型五 同解同构
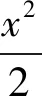
分析:实际上题目中包含两条二次曲线,分别是椭圆和三角形得外接圆.它们的特点是都过A、B两点,故可以考虑利用方程同解来解决.
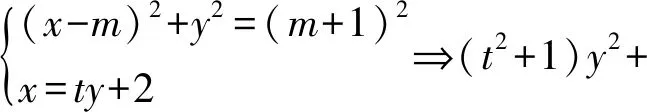
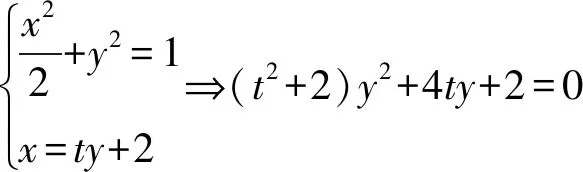
点评:如果两个同类型的方程同解,那么对比系数,一定有对应系数成比例.利用这一特点,我们设法构造同解方程,从而大大减少了计算量.实际上,这种同构方式对外接圆问题尤为有效.
3 学会借力打力 提升综合素养
通过以上实例,我们能够切实的感受到同构式在求解解析几何试题的过程中所带来的便捷性,构造合适的同构式,写出同构方程,往往能够有出其不意的效果.实际上,解析几何中所涉及的同构类型不仅仅包括双切圆同构、平行弦的点式同构、切线同构、斜率同构和同解同构,例如在同构同解类型中,不单单可以是坐标点的同构同解,还可以是斜率的同构同解.同构式类型多样,不同的题型需构造不同的同构式,但万变不离其宗.正如前面所说的,同构式就是一把解题“利器”,我们要学会借力打力,巧用同构式击破解析几何试题.我们将这种构造同构式的方法总结为:一生二,二生三,三生万物!一生二,就是点M(x1,y1)满足方程x0x1+y0y1+c=0,则会存在第二个点N(x2,y2)满足方程x0x2+y0y2+c=0;二生三,那么根据两点确定一条直线,由M,N两点确定的直线方程为:x0x+y0y+c=0;至于三生万物,有了一轮同构,那么还可以来第二轮同构.
在这样一个探究学习过程中,让学生能深刻地看待问题,不仅可以促进学生对知识的深入理解,又能开发学生的数学解题思路和解题方法,进一步提高学生的综合素养.

