考研数学中的幂级数求和函数问题

吴德福，李艳春

(吉林建筑科技学院基础科学部，吉林长春，130000)

幂级数求和函数是考研数学中的重要内容，其中涉及到的方法与技巧非常多，处理起来也非常灵活，本文根据历年考研真题总结归纳出了一些求和函数的常见方法和题型.

1 预备知识：幂级数的和函数的分析性质

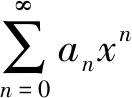
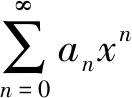
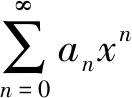
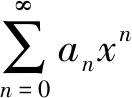
2 幂级数求和函数的常用方法总结

方法1：套常用公式

把常见函数展开成的麦克劳林级数反过来用，就得到了一些具有特定形式的幂级数的求和函数公式.下列基本公式就是解题中频繁出现的，也是命题人出题的依据，应该熟稔于心.

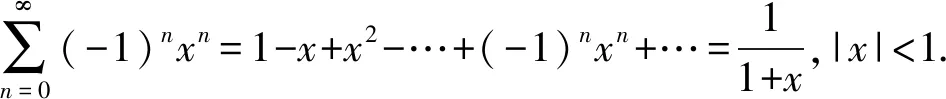
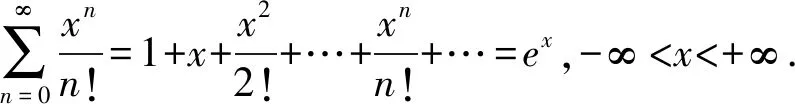
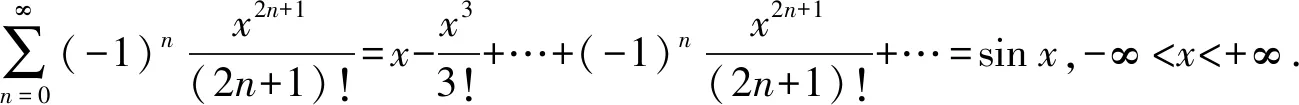
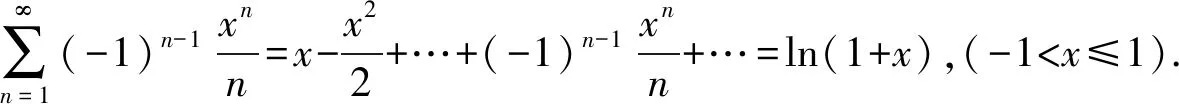
分析对照常用公式，发现此级数与公式(5)比较类似，所以可以从此公式入手，将所求级数构造成公式(5)的形式，从而借助公式(5)完成解题.

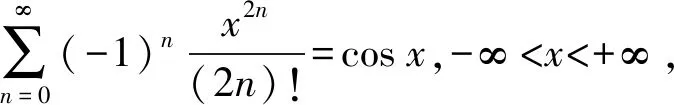
方法2：先导后积

利用幂级数和函数的分析性质，对于级数的系数是分数，且分母中含有n的一些类型，可以先逐项求导消去系数分母中的n，利用方法1中的公式求出和函数，然后再逐项积分还原求得原级数的和函数.

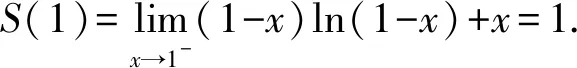
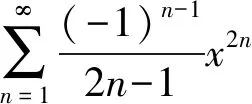
从而S(x)=xarctanx，x∈[-1,1].

方法3：先积后导

利用幂级数和函数的分析性质，对于级数的系数是关于n的多项式的这种类型，可以先逐项积分消去系数中的n，利用方法1中的常用公式求出和函数，然后再逐项求导还原求得原级数的和函数.

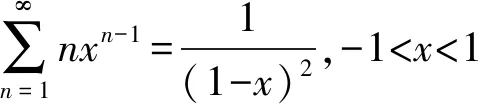
一般地，形如∑(kn+b)xkn的幂级数求和问题都可以采用先积后导的方法解决.

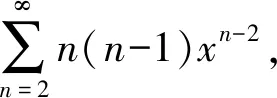
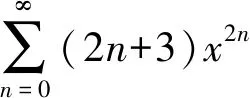
分析形如∑(kn+b)xkn的幂级数，可以分解为∑(kn+b)xkn=∑(kn+1)xkn+(b-1)∑xkn，其中∑(kn+1)xkn可以用先积后导的方法求和函数，∑xkn可以用等比级数的结论求和函数.

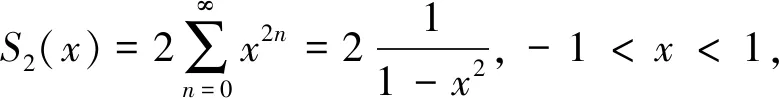
方法4：验证幂级数满足所给的微分方程，并通过解微分方程求和函数

对于某些幂级数，想直接求解出和函数有难度，为了降低难度，命题人一般会分两步来命制试题：(1) 验证和函数满足所给的微分方程；(2) 求和函数.这类问题可以利用和函数S(x)可以逐项求导的性质，求出S′(x),S″(x),…，验证其满足所给的微分方程.在解微分方程求和函数时，注意隐藏的初始条件，根据幂级数的表达式，不难得到S(0),S′(0),S″(0),…的值，根据这些初始条件就可以确定微分方程通解中的任意常数从而求得和函数.

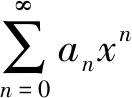
分析题干中给出了系数的递推式，因而可以求出系数an的具体表达式，进而寻找求和函数的方法.但本题第一问让证明S(x)满足的微分方程，这样就指明了解题方向，降低了难度.实际上，本题可以去掉第一问，让学生自己去找S(x)所满足的微分方程，这样设置就加大了题目难度.

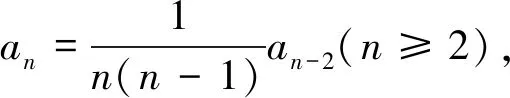
(Ⅱ) 解微分方程并注意到初始条件S(0)=a0=3，S′(0)=a1=1，得S(x)=2ex+e-x，-∞

方法5：建立和函数满足的微分方程并求和函数

某些幂级数的和函数S(x)用常规方法很难求得，这时可以考虑求出S′(x),S″(x),…，根据所给的系数an,an+1,an+2,…的关系式建立起S(x)所满足的微分方程，并根据隐藏的初始条件S(0),S′(0),S″(0),…的值求出和函数.

分析根据所给的幂级数系数的递推式求解{an}的表达式是比较困难的，可以利用它来构建和函数所满足的微分方程，并通过求解微分方程的方法求出和函数.

以上仅列举了考研数学中使用较多的方法，事实上，有些求和函数的问题需要多种方法综合使用，需要读者对各种方法能够熟练运用，融会贯通.