透过圆“看”圆锥曲线

唐如强

(浙江省余姚市第八中学，浙江余姚，315400)

圆是我们最早接触的图形之一.圆的几何性质相对于圆锥曲线要简单得多，更容易让我们所接受.下面介绍几个通过类比圆的性质来得到圆锥曲线的性质的实例，投石问路，与读者共飨.

1 圆与圆锥曲线的性质

1.1 垂直弦问题

圆性质1：等于直角的圆周角所对的弦过圆心(直径).

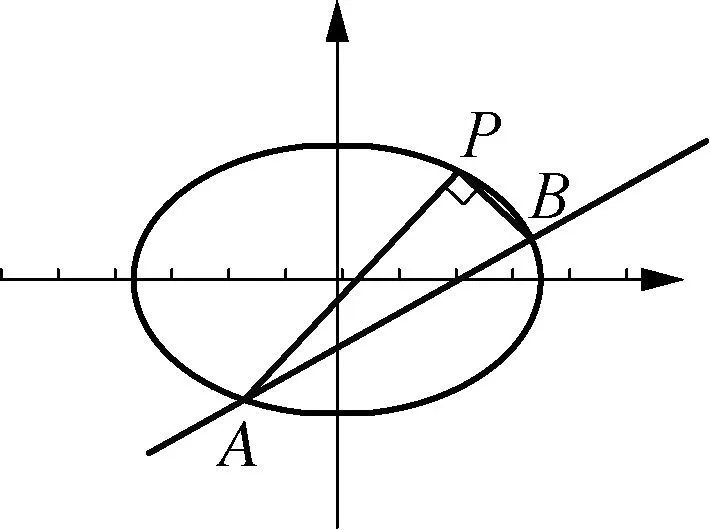
类比圆性质，我们可以得到椭圆的一个性质：

(1) 椭圆性质： 过椭圆上一点作互相垂直的两条弦，则该直角顶点所对的弦必过一个定点.

求证：直线AB必过一个定点.

证明：当直线AB斜率不为0时，设直线方程x=my+n，A(x1,x2),B(x2,y2)

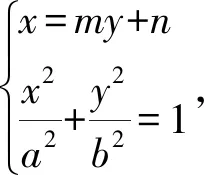
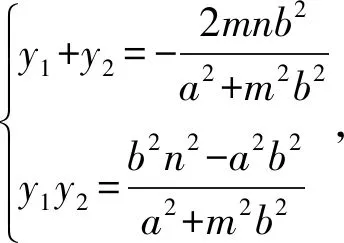
因为PA⊥PB，

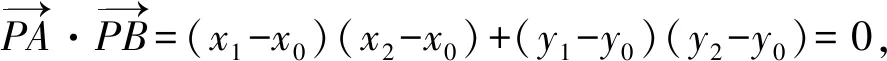
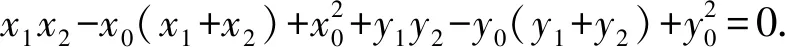
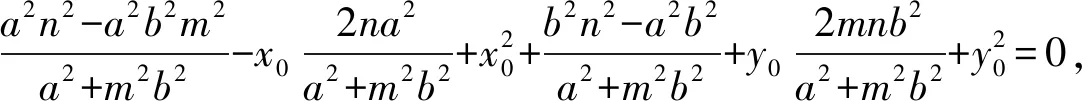
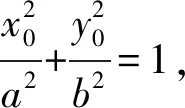
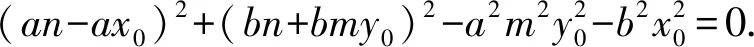
两两组合，平方差得a2(n-x0+my0)(n-x0-my0)+b2(n+my0+x0)(n+my0-x0)=0，

所以 (n-x0+my0)(a2n-a2x0-a2my0+b2n+b2my0+b2x0)=0.

因为点P不在直线AB上，所以n-x0+my0≠0，

所以a2n-a2x0-a2my0+b2n+b2my0+b2x0=0，

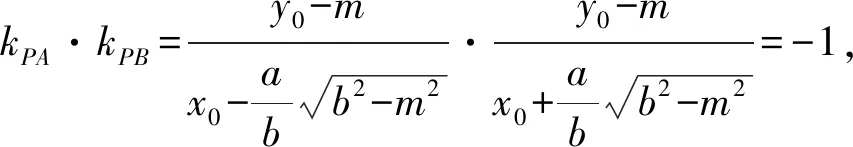
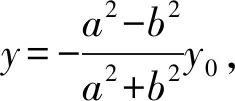
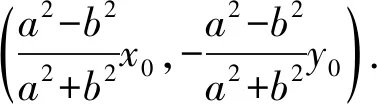
类似地，我们也可以得到双曲线，抛物线上的性质.

(2) 过双曲线上一点作互相垂直的两条弦，则该直角顶点所对的弦必过一个定点.

(3) 过抛物线上一点作互相垂直的两条弦，则该直角顶点所对的弦必过一个定点.

以上性质的证明在这里不再赘述.结合三个性质，我们容易得到圆锥曲线的统一性质：

(4) 过圆锥曲线上一点作互相垂直的两条弦，则该直角顶点所对的弦必过一个定点.

1.2 中点弦问题

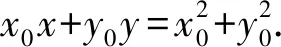
类比圆性质2，圆锥曲线也有类似性质：

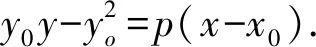
利用点差法很容易证明以上性质，本文省略这一证明过程.需要指出的是，以上各性质在形式结构上与各自的圆锥曲线方程保持一致，体现出代数式整体和局部的整齐性和对称美.利用上面结论，我们很容易解决中点弦问题，与点差法解题比较，特别是选择、填空题，可以免去重复繁琐的计算，提高解题效率.

1.3 切线方程问题

圆性质3：过圆：x2+y2=r2上一点P(x0,y0)引圆的切线，则切线方程为：x0x+y0y=r2.

类比圆的切线方程，我们同样可以得到圆锥曲线的切线方程：

(3) 抛物线y2=2px及抛物线上一点P(x0,y0)，则过P点的切线方程为：y0y=p(x+x0).

圆性质4：过圆：x2+y2=r2外一点P(x0,y0)引圆切线，则切点弦所在直线方程为x0x+y0y=r2.

类比圆性质4，我们有：

(3) 过抛物线y2=2px外一点P(x0,y0)引抛物线的切线，则切点弦所在直线方程为：y0y=p(x+x0).

对于双曲线和抛物线，我们也可以得到类似结论，这里不再论述.

圆性质5：过圆x2+y2=r2内一点P(x0,y0)作直线与圆相交，则过交点的圆的切线的交点的轨迹方程为x0x+y0y=r2.

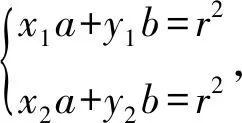
类比性质5，我们有：

(3) 过抛物线y2=2px内一点P(x0,y0)作直线与抛物线相交，则过交点的抛物线切线的交点的轨迹方程为y0y=p(x+x0).

2 结语

开普勒曾说“我珍惜类比胜于任何别的东西，它是我最可信赖的老师，它能揭示自然界的秘密.”透过圆的性质，通过类比、联想、迁移、推广，去获得圆锥曲线的相关性质，增加了数学知识的横向类比建构，加深了对相关知识的了解和认识，同时，通过对数学类比尝试体验，学习了数学创新的一种途径，提高了数学创新思维能力.