践行结构化板书：基于学程，渐次生长——以“算术平方根”新授教学为例

张小丽

(江苏省海安市紫石中学，江苏海安，226600)

最近在本地区初中数学教师全员集中培训活动中，笔者有机会执教《义务教育教科书》七年级下册“算术平方根”一课，取得较好的教学效果．特别是本课践行了全国著名特级教师李庾南老师倡导的“结构化板书”[1]，下面梳理该课教学流程、板书设计并阐释设计意图，提供教学研讨．

1 “算术平方根”新授课教学过程

活动(一) 基础回顾

问题1：同学们之前已经学过了哪几种运算？你觉得这些运算之间有怎样的关系？其中互为逆运算的是哪几种运算？

师生活动：学生回答有困难．可以先回顾乘方的有关知识：an，a叫底数，n叫指数，an也叫幂．

问题2：要剪出一张边长是5厘米的正方形纸片，它的面积是多少？

师生活动：这个问题就是求：52=？此时已知底数和指数，求幂，是乘方运算．同时生成以下板书：

问题3：让我们逆向思考，如果想剪出面积为25平方厘米的正方形纸片，同学们能求出它的边长吗？你们能列出怎样的式子求解？

师生活动：这个问题就是要求一个正数，使它的平方等于25，即：(？)2=25．此时已知幂和指数，求底数． 这样的运算叫开方运算．同时生成以下板书：

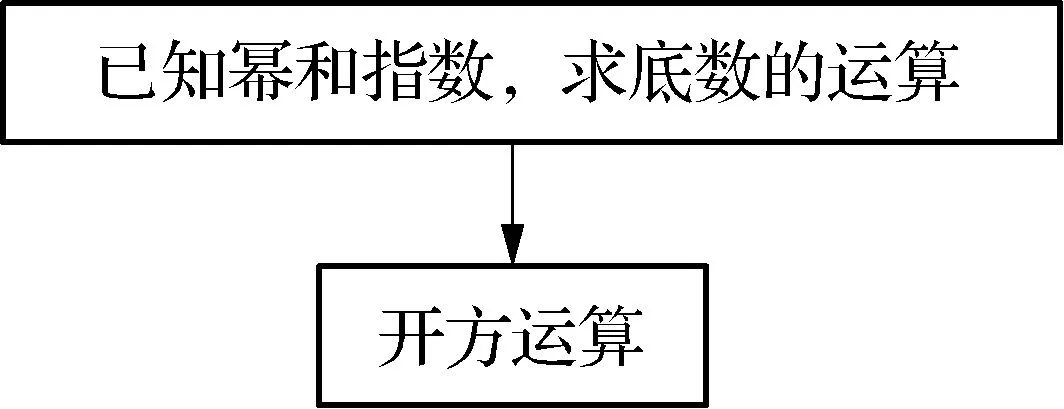
现在可以回答问题1：乘方运算与开方运算互为逆运算．同时生成以下板书：

问题4：请观察下表，结合正方形面积与边长的关系，完善表格：

正方形的面积191636425正方形的边长

师生活动：这个问题的实质是：已知一个正数的平方，求这个正数．我们设这个正数为x，这个正数的平方为a．我们称这个正数x叫做a的算术平方根．明确定义之后，教师写出板书：

设计意图：通过设置问题串，引导学生回顾已经学过的知识，类比之前学习过的加法和减法，乘法和除法之间的互逆关系，自然而然引出乘方的逆运算．问题4，从具体到抽象，给出了算术平方根的概念，使学生能够更好地理解算术平方根的意义．

活动(二) 概括新知

1.1 认识概念

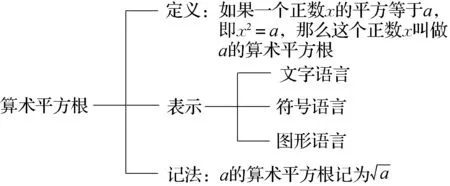
师生活动：师生共同理解算术平方根的定义：如果一个正数x的平方等于a，即x2=a，那么这个正数x叫做a的算术平方根，强调x为正数．老师板书：

定义：如果一个正数x的平方等于a，即x2=a，那么这个正数x叫做a的算术平方根．

1.2 例题学习

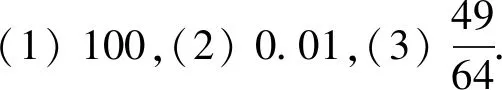
设计意图：例1的设计是为了引导出板书中的算术平方根的文字语言和符号语言．同时，师生互动，生生互动，体现求一个正数的算术平方根的思考过程．

追问：例1展示的是一组正数的算术平方根的结果都是有理数，是不是所有的正数的算术平方根都是有理数呢？我们来看问题5．

问题5：能否用两个面积为1的小正方形拼成一个面积为2的大正方形？大正方形的边长是多少？

问题6：0的算术平方根是多少？

问题7：-1的算术平方根是多少？

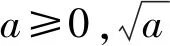
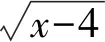
通过例2的学习生成以下板书：

2 对结构化板书的实践与思考

第一，结构化板书，体现知识的整体结构

本节课采用了“自学·议论·引导”教学法的结构化板书设计[2]，让学生对本节课所学的知识结构一目了然．笔者在执教本节课内容时，对算术平方根的表示方法只列出了两种：① 文字语言;② 符号语言．后经评课老师提醒，知道还可以补充图形语言，从而使表示方法更完整．顺便提及，教学或组织学生研究一个新的数学对象时，要尽可能将这个数学对象的文字语言、图形直观、符号语言(表示)都要进行必要的板书.

第二，结构化板书，促进概念的自然生成

本节课是人教版七年级下册第六章“实数”单元的章节起始课．学生学习了加法与减法，乘法与除法互为逆运算．因此，学生学习乘方的基础上，思考乘方是否也有逆运算？从而引出本节课．符合学生的认知规律，算术平方根的研究也就水到渠成了．可见，基于“互逆思想”的研究方法是应该向学生进行传递和训练的，有利于学生今后独立研究数学问题时，善于逆向分析、举一反三、成果扩大.

第三，结构化板书，基于问题串渐次生长