聚焦核心问题 提升学生素养

林秋灵

(安溪县沼涛实验小学，福建泉州，362000)

《义务教育数学课程标准(2022年版)》提出教学目标的本位教学就是“核心素养”，让孩子们会用数学的眼光去观察现实世界、会用数学的思维去思考现实世界、会用数学的语言去描述现实世界[1].核心素养导向的教学就是把学科知识转化为学生核心素养的过程.在教学实践中，我们可以用核心问题引领“大单元”教学，积极开展主题化、项目式学习等综合性教学活动，促进学生举一反三、融会贯通，加强知识间的内在关联，促进知识结构化，让学生有效探究、真实体验、深度学习，有效地提升核心素养.

1 着眼本质，设计核心问题

核心问题是课时、单元、知识板块、知识领域中孩子们需要学习、探究的中心问题[2].学生思维零碎、刻板和浅表化是现实教学中存在的问题，教师应该关注知识本质，着眼学生发展，融通关连，用核心问题引发学生阅读、操作、思考、表达、分享争辩等，经历知识的探索和形成过程，促进学生对所学内容的深刻理解和掌握.

1.1 追本溯源，合理设计

数学知识间存在着千丝万缕的联系和内在的思维逻辑，教师要抓住知识的本质，打通知识间的通道，科学适度地“越位”，设计有效的核心问题，将分散的知识点“连珠成串”，发展学生的思维.例如人教版三下的第二单元复习课中，用核心问题“除法可以从低位算起吗”任务驱动，让孩子们自觉投入到除法的复习课，通过对核心问题的讨论，加深学生对除法意义、除法算式的算理和算法的理解，追溯到除法的数学本质——计数单位的平均分.核心问题引领下的课堂应实现学生的主体性，关注孩子们的成长.核心问题要紧扣核心概念、知识本质来设计，当学生们能紧扣核心问题展开深度学习——思考、讨论、争辩、质疑，除法的算理算法就水到渠成地掌握了，还体验了比较、辨析、验证来解决问题的过程，体验了学习的乐趣.

1.2 答疑解惑，有效提炼

有些数学教学内容比较多，孩子们学起来觉得“每个知识都很重要，分开来容易忘记，组合起来又容易混淆”，特别是单元整理和复习或总复习课.如六下《数的认识总复习》，知识纷繁，怎样区分整数、自然数、正数、负数、分数、小数、百分数还有计数单位等.针对孩子们的困惑，我们可以梳理知识点，用核心问题整合知识，化繁为简，培养数感.

《数的认识总复习》学习单

核心问题1：你能用自己的方式整理学过的数吗？

核心问题2：你能在数轴上找到不同的数，并说说组成并判断大小？

在解决第一个核心问题时，孩子们按不同的标准来分类整理学过的数，精彩纷呈：

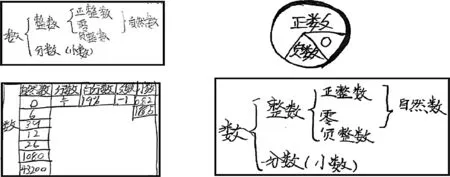
设计“核心问题”时首先要思考如何打通新旧知识间的通道，合理用教材，关联整合，有效提炼；然后思考要怎样构建网络，用“核心问题”来统领相关内容的教学，起到纲举目张的作用.

2 单元整合，提炼核心问题

《义务教育数学课程标准》(2022年版)倡导从“教中心”走向“学中心”，基于学生的需要进行教学，体现学生学习的主体地位.我们可以用“结构化”的教学理念，融合调整教学内容，提炼核心问题，设计实施“大单元”教学，让低阶思维走向高阶思维，践行深度学习，发展学生核心素养.

2.1 “大”视角，提炼核心问题

新课标理念下的“大单元”教学，其内容的确定，可以是按教材内容组织，也可以按学科学业发展和学科核心素养发展的进阶来组织，还可以按真实情境下的学习任务跨学科组织[3].这时就需要教师“跳”出来，俯瞰教材，提炼核心问题.例如小学数学图形与几何领域中，各种图形之间关系的认识——“图形的认识与度量”，主要是围绕“度量问题”展开的.所有的度量和度量单位，其中的量都是通过数来表达，并且都是基于1度量单位进行表达的，不同的是1的后面必须缀有度量单位称谓.所以在教学时应自始至终，就清晰地指出相应的“核心问题”——度量时需要什么样的标准(统一度量单位)，以及如何进行度量(得出数量)，同时在整个阶段所有的学习历程中，也应不断重复这些问题，真正实现提纲挈领的作用.

2.2 “微”聚焦，提炼核心问题

在提炼核心问题时，我们需要有一双素养发展的“大单元”教学慧眼.如人教版四下《小数的意义和性质》这一单元，先用核心概念梳理本单元的知识网络，如图：

然后在“大单元”分课时设计时，聚焦“核心概念”的梳理图，合理提炼核心问题：

教学内容核心问题设计课时1小数的意义 核心问题1:为什么要学习小数?核心问题2:计数单位间有什么关系?核心问题3:学习小数有什么作用?课时2小数的读法、写法核心问题1:3.65表示什么意思?结合生活中的情境举例说明.核心问题2:用数位顺序怎么表示出3.65?核心问题3:你能说说珠穆朗玛峰高8844.43米这个数字的含义吗?可以用哪种方式来表示这个数?(计数器、示意图等)课时3小数的性质和大小比较核心问题1:0.3=0.30,请你用自己喜欢、别人听得懂的方式解释说明.核心问题2:为什么整数末尾添上0或者去掉0,数的大小发生了变化? 课时4小数点位置移动引起小数大小的变化 核心问题1:0.28×100=28, 0.28和28之间发生了什么变化?什么变了,什么没变?核心问题2:0.7、7、70、700这四个数之间具有怎样的关系?结合生活实例说一说,你从中发现了什么规律?这规律和计数单位有什么关系?课时5小数与单位换算核心问题1:她的身高2.26米,你还能换个说法吗?核心问题2:单名数和复名数之间在改写时需要注意什么? 课时6小数的近似数核心问题1:结合调查的信息,说一说你改写的经验,学习改写有什么作用?核心问题2:用“四舍五入”法求近似数有价值吗?请举例说明.核心问题3:一个三位小数四舍五入后是8.65,这个三位小数可能是多少?

当我们用“大单元”教学的角度，把每部分教学内容围绕核心概念“计数单位”提炼核心问题，构建知识网络，既体现了知识间的内在联系，又凸显了核心概念的核心地位，一举多得.

3 评价反馈，落实核心问题

《义务教育数学课程标准》(2022年版)对“内容要求”提出了“学业要求”和“教学提示”，细化了评价与考试命题建议，注重实现“教—学—评”一致性.核心问题提炼了，如何让学生紧扣核心问题进行探究，如何检测学习目标是否达成？结合五上《多边形的面积》的“大单元”设计实施来说明.

首先，明确“教学评”一体化的流程图.

其次，教学设计也要有所改变，模板如下：

年级五年内容平行四边形的面积教师陈老师课标描述核心素养:空间观念、推理能力单元主题:转化思想教材分析平行四边形的面积是一种相对不规则的图形,其面积的计算有难度.本节课主要让孩子们回忆长方形面积的计算方法,把平行四边形转化成长方形的面积,得出平行四边形的面积=底×高.学习重点经历平行四边形面积公式的推导过程.核心问题 1. 独立思考:为了便于研究,将平行四边形可以转化成哪种图形?2. 思考交流:转化前后的变化与联系?3. 平行四边形的面积公式是怎样的?你的想法是什么?学情分析学生已经掌握了长方形和正方形的面积计算方法,了解平行四边形的形体特点.如何转化,可以让孩子们动手实践,体验转化的过程,适当采用媒体辅助.学习资源平行四边形纸片几个、剪刀等.学习目标 1. 动手操作,利用转化将平行四边形转化成长方形,观察比较转化前后的变化和联系;2. 思考描述转化前后的变与不变,推导出平行四边形的面积计算方法;3. 基于例题,解决生活中有关平行四边形面积的问题.评价任务 1. 能将平行四边形转化成长方形引发猜想;2. 能说出转化前后的相同点和不同点,并推导出面积公式;3. 能利用公式计算例题并解决生活中有关平行四边形面积的问题.评价设计学习活动活动要求(问题引领)行为表现教的活动(根据预设做出应对策略)

最后，做好相对应的达标测评，可以分层设计——基础题、标准题、挑战题，让学生根据自己的特点合理选择；可以采用对答案、同桌互改、小组长批改等多种方式，当堂完成，并整理出存在的共性问题，并于下节课及时补缺补漏.

总之，在新课标理念的引领下，我们要落实素养本位教学，用核心问题统领课堂，核心问题引领下的数学课堂是开放的、富有生命力的、更具挑战性的课堂.我们应该留给学生更多课堂时间和思维空间，最大限度地把课堂还给学生，让学习真正的发生，让学生素养提升水到渠成.