重视“含参”问题教学，理解螺旋上升要求——以人教版七年级上册教材习题为例

邓厚波

(江苏省海安市城南实验中学，江苏海安，226600)

学生从小学进入初中后，首先经历了有理数系和实数系的两次数系扩充，进而研究数系扩充后的运算；接着就是系统研究字母表示数，从数到式后，又分别研究整式及运算、分式及运算、二次根式及运算，这些数、式的运算与变形的技能是学习方程和函数的基础．以上都是初中阶段代数研究的主要问题．贯穿在代数学习历程中的还有一类重要的数学习题，那就是“含参”问题，从七年级到九年级，可谓在代数学习全过程，也是值得我们重视的，而且“含参”问题在不同年级的出现和分布也体现了螺旋上升的教学要求．本文以人教版七年级上册教材的一些典型“含参”习题为例，谈谈我们对这类问题的教学理解．

1 七年级上册教材中“含参”问题及教学理解

案例1(摘选自《有理数》)计算(-2)2，22，(-2)3，23.联系这类具体数的乘方，你认为当a<0时，判断下列各式是否成立？

(1)a2>0；(2)a2=(-a)2;(3)a2=-a2;(4)a3=-a3.

教学理解：这道题从特殊到一般，让学生对比互为相反数的两个数的平方、立方的结果有怎样的关系，然后针对负数让学生判断4个等式是否成立．问题的本质是让学生研究、归纳出负数的乘方的符号规律，教材在此前学习乘方运算时已用“文字语言”进行过小结，但并没有给出符号表示，在习题中进行渗透符号表示的意识，这样一种“安排”值得研究和细思．还有，值得注意的是，这里的字母就不再是一个常量，而成为一个变量，参数的味道在《有理数》这一章就已显现出来．

案例2(摘选自《有理数》)结合具体数的运算，归纳有关性质，然后比较下列数的大小：

(1) 小于1的正数a，a的平方，a的立方；

(2) 大于-1的负数b，b的平方，b的立方．

图1

教学理解：解题方法仍然是先举例运算后比较大小，再归纳出它们的大小规律．由于初步认识一个限制范围内正数的平方与立方的大小比较，所以教学时只需要学生举几个例子，然后进行归纳即可，这时还不能进行更一般的演算证明，这也是螺旋上升的一个重要特征．比如，随着以后函数的学习，借助函数图象还可进行更加形象直观的解释(如图1)．

案例3(摘选自《整式加减》)一个两位数的个位上的数是a，十位上的数是b．

(1) 列式表示这个两个数．

(2) 这个两位数与它的10倍的和是11的倍数吗？

教学理解：进入《整式加减》一章之后，难度比《有理数》稍稍增大，具体来说，有理数一章还是先从具体的数进行运算后再猜想性质，走向一般的归纳概括，而用字母表示数之后，引出整式的概念和整式加减，则像这道题就不再安排具体的数字，让学生运用所学的整式的加减进行运算分析，得出的结果中分析出“公因数”11即可判断，它们的和是11的倍数．可以发现，这里不但需要整式加减运算的能力，而且最后的“提取公因数”是逆向运用乘法对加法的分配律，也是为八年级学习提公因式法因式分解进行的必要准备和知识铺垫．

案例4(摘选自《整式加减》)甲地的海拔高度是hm，乙地比甲地高20 m，丙地比甲地低30 m，列式表示乙、丙两地的海拔高度，并比较这两地的高度差．

教学理解：这里的先安排列式表示乙、丙两地的海拔高度还是为比较两地高度差做的必要铺垫式问题，在此铺垫设问基础上可以作差比较，从而运用整式加减可以合并同类项，消去h，得到两地高度差是一个常数．这个问题的在小学阶段也曾出现过，比如一道相对较有难度的小题习题是：已知乙地比甲地高20 m，丙地比甲地低30 m，请比较这两地的高度差．小学生当时的处理方法是算术方法，直接列式20+30=50．但是这种算式的道理解释不如上面的“案例4”来得更好理解．这也就是说，随着学习的深入，新概念、新工具的引入，过去曾经理解有困难的问题，可以获得更加自然、简单、更有说服力、更具推广性的处理．这也正是我国著名数学家李大潜院士指出的“数学愉悦感”的源泉．

案例5(摘选自《整式加减》)把(a+b)和(x+y)各看成一个整体，对下列各式进行化简：

(1) 4(a+b)+2(a+b)-(a+b);

(2) 3(x+y)2-7(x+y)+8(x+y)2+6(x+y).

教学理解：“看成整体”是一种十分重要的数学能力或处理问题的着眼点，从七年级《整式加减》开始，教材上就这样设计习题，引导师生重视“看成整体”的解题策略．这方面的题例有很多，这里可分别列出以下几道体现“看成整体”的一些题例，看看它们在不同年级的考查形式是怎样的？

例1：(七年级)如图2，数轴上点A，B分别对应数a，b．其中a<0，b>0．

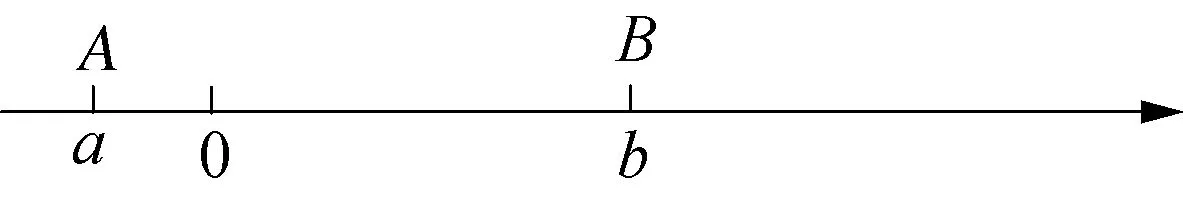
图2

若该数轴上另有一点M对应着数m．当m=2，b>2，且AM=2BM时，求代数式a+2b的值．

解读：这里虽然a，b都没有给出具体的数值，但是根据“形”(线段之间)对应的数量关系，可以列出它们对应的等式(运用数轴上两点之间距离公式)，再进行等式变形即可整体获得a+2b的值．

例2：(八年级)我们知道，可以利用“杨辉三角”展开(1-2x)4=a0+a1x+a2x2+a3x3+a4x4，那么代数式a1+a2+a3+a4=．

解读：如果“真的”利用“杨辉三角”展开后再求代数式的值，用时较多，如果能想到赋两个特殊值0，1，分别代入原等式，就可整体求解，快速解答．这里虽然是一种技巧解法，却也是认真观察问题的题设与结论的特点，而获得的一种优解、简解．在这里，眼力的高低决定了算法的繁简．

2 关于“含参”问题教学的进一步思考

第一，研究学段内各册教材，梳理“含参”问题的分布情况

研究教材是很多老师在开设公开课或阶段命题制卷时都会重视的一项基础研究，然而教材研究还有一个重要的关注点，就是对比研究学段内各册教材，将各册教材中都会关注的一些共性问题、经典问题[1]，梳理出来，深入对比研究．像上文我们关注的“含参”问题，在不同年级的教材中，都有大量的分布，如果能全面梳理出来，对比研究，就能找准教学的重点，在新授课教学的例题选编、作业设计、单元命题制卷时，都会重视这类问题的设计和考查．就不会被一些“网红题”带偏选题方向，而能够找准教学的用力点．

第二，把握各年级教学要求，通过“含参”问题来传递方法

在研究、梳理出各年级教材中“含参”问题之后，一个重要的研究工作就是要对比“含参”问题在各年级的教学要求，这样可以在作业设计时做好选题改编的难度控制，既不要人为拔高，也不要用大量雷同的同类题让优秀学生“空转”训练．此外，另一个选题与讲评的重要追求是，通过这些“含参”问题的训练来向学生传递解题方法，比较重视“回到定义去解题”，重视“数形结合”，重视“分类讨论”，等解题思想方法．

第三，重视复习课选题研究，“含参”问题可作为复习主线

复习课有很多类型，比如单元复习、章末复习、期中复习、期末复习、中考一轮复习、中考二轮复习、中考专题复习等等，这些不同阶段的复习课中，往往也会出现“含参”问题的身影，但是如果将“含参”问题作为一个复习主线进行构思，研究“含参”微专题复习课就是值得尝试的一类课型了．比如，在七年级期末复习时，“含参”微专题复习课就要兼顾“含参”问题在不同章节中的分布，比如有理数中“含参”问题有哪些类型，比如整式加减或一元一次方程中“含参”问题，再比如以“含参”问题“联通”不同章节的综合题，等等．当然，这样的微专题复习课目前在中考复习阶段比较多见，在七、八年级的阶段复习课中还值得进一步研究．